农业循环经济发展研究——以安徽省为例

吴 洁，陈益杨，张海珍，朱家明

（1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030；2.安徽财经大学 金融学院，安徽 蚌埠 233030）

我国是个人口大国，农业是我国的一大产业，是我国经济发展的根本。我国的耕地面积占世界总耕种面积的9%，水资源占有量是世界总水资源量的6%，但是我国的人口却是世界总人口的22%，人均比例的悬殊是我国农业发展的压力所在。同时，投入与产出比例低下、过度依赖资源的消耗、低效益、生态环境恶化严重等问题严重制约着我国农业的快速发展。因此在资源约束和绿色循环农业经济的前提下，研究如何提高化肥利用率、农田灌溉效率以及减少对环境的污染是十分必要的。这也是本文研究的意义所在。

1 农药、化肥施用量与粮食产量关系研究

1.1 研究思路

我国总的耕地面积占世界的9%，但是我国的人口却占世界总人口的22%。因此提高耕地利用率，增加粮食产量对于我国经济发展具有重要意义。绿色循环农业[1]的发展理念要求我们必须利用有限的资源，创造出最大的产量。而且要在绿色与循环的理念支撑下发展农业。本文首先选取与粮食产量相关的指标，建立了基于多元线性回归的粮食产量模型。用以研究化肥、农药、粮食产量之间的内在关系。并探究在减小农药对环境污染的前提下，如何促进粮食产量的提高。并根据研究的结果提出了相应的建议。

1.2 研究方法

1.2.1 基于多元线性回归的粮食产量模型

在中国统计年鉴上找到相关数据如表1：

表1 安徽省历年粮食产量、农药使用量、化肥施用量数据表

1）理论知识介绍

有多个自变量的线性回归成为多元线性回归模型[2]。假设y是一个可观测的随机变量x1,x2,…xk为k个自变量，且有

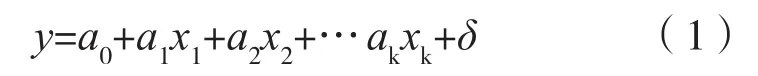
其中：a0,a1,…ak是未知参数；δ为随机误差，且δ服从N（0，σ2）。（1）式称为k元线性回归模型，自变量x1,x2,…xk也成为解释变量，因变量y也成为内生变量。现假定对于变量y与自变量x1,x2,…xk已得到n组观测数据见表2：

表2 y与xi的观测值表

在理论模型式（1）下，可以认为表中的数据满足

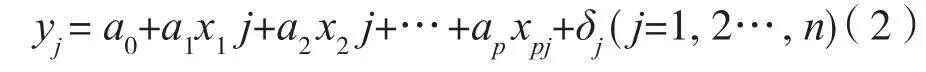
（2）式中：δj为相互独立且都服从N（0，σ2）的随机变量。若记

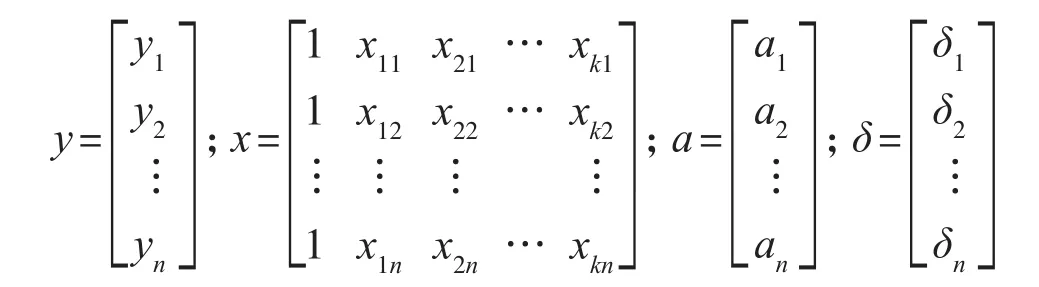
则可用矩阵表示为

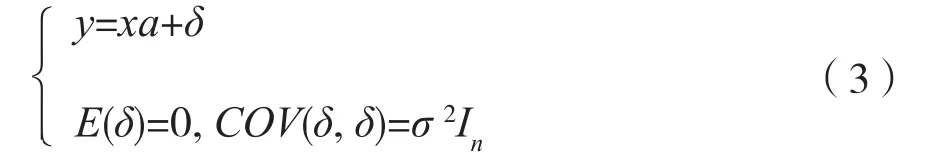
则模型式（3）式简记为(y,xa,σ2In)。

2）结果分析

将相关数据代入多元线性回归的粮食产量模型，在MATLAB中求解得：

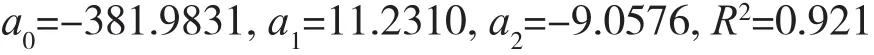
根据求解结果可得粮食产量（y）与化肥施用量（x1）、农药使用量（x2）之间的多元线性回归模型为：y=-381.9831+11.2310x1-9.0576x2。根据拟合的方程可以看出，化肥施用量每增加1个单位，粮食产量将增加11.23110个单位。农药每增加1个单位，粮食产量将减少9.0576个单位。因此在绿色农业、循环农业经济主题的倡导下，我们应该在保证农作物对化肥农药需求的前提下，适当地减少农药的使用量，适当地提高化肥的使用量。只有这样，才能促进粮食产量的提高，减少农药对环境造成的污染。

拟合的残差图如图1所示：

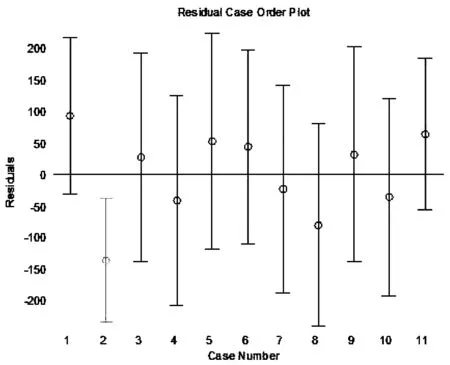
图 1 拟合残差图

根据求解结果可知可决系数R2=0.9211，拟合度较高，拟合效果较好。

1.2.2 化肥利用提高率的研究

首先，根据粮食产量的数据在MATLAB中编程得到了粮食产量与时间（t=1, 2, …n）的关系，运行结果：y=71.56t+2607。拟合图如图2所示：

根据求解结果可知拟合的可决系数R2=0.9373，拟合度较高，拟合程度较好。将t=16代入上式即可预测出2020年的粮食产量为3751.96万吨。

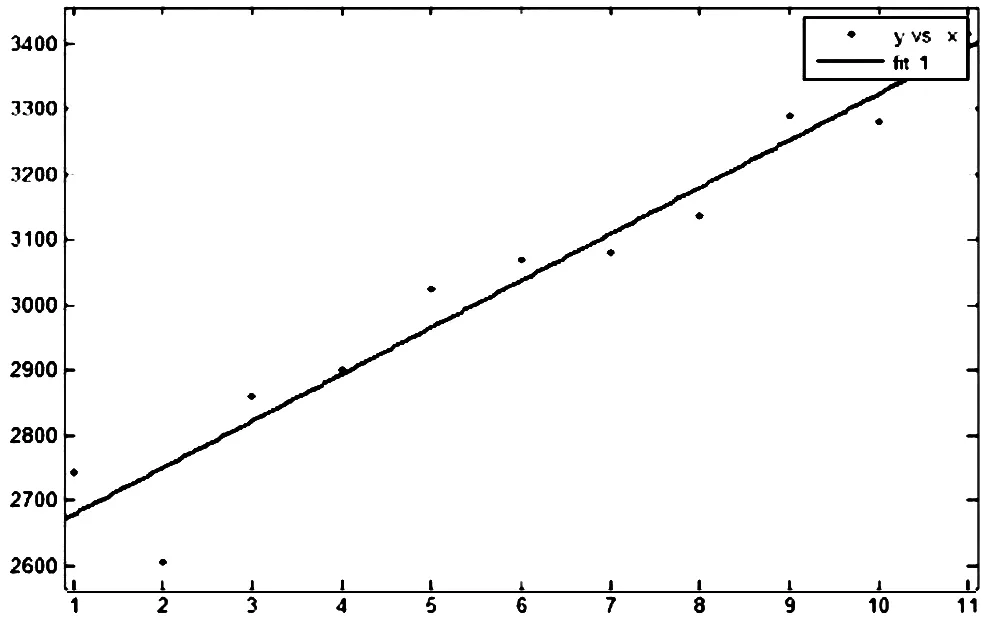
图 2 拟合图

然后，定义：化肥农药配比率=化肥施用量/农药使用量。根据化肥施用量与农药使用量历年的数据可得2005-2015年的化肥施用量与农药使用量配比率，如表3所示：

通过观察表格，我们可以看出历年化肥农药配比率总是维持在某一个固定值之间上下波动，也就说明在种植农作物的过程中化肥与农药的使用量的比率是一个固定值，这里我们选取平均值作为固定值。所以可得化肥施用量与农药使用量的关系为：

r=x1/x2=28.64，也即x2=0.0349x1

表3 历年化肥农药配比率

最后，求解化肥利用率提高的百分比。

首先，根据粮食产量与化肥施用量、农药使用量的函数关系和化肥施用量与农药施用量的配比关系可得如下方程组：

然后，在保证化肥施用量和农药使用量零增长的前提下，求解化肥利用率提高的比率。则可以列出如下方程组：

若假设化肥和农药的使用量在零增长的绿色循环发展理念下，根据测算到2020年化肥的利用率将会提高10.948%。

2 农田灌溉效率研究

2.1 研究思路

研究农田灌溉效率[3]是绿色循环农业发展的又一重要方面。针对农田灌溉效率问题，首先运用主成分分析法确定影响农田灌溉利用效率的主要因素。然后利用由主成分回归、灰色预测、最小二乘法构成的组合预测模型预测出2020年的农田灌溉效率值。并给出了相应的建议。

2.2 研究方法

2.2.1 主成分回归预测

主成分回归[4]就是首先利用主成分分析法找出来几个主要的影响因素，然后在MATLAB中，根据选取的主影响因素和因变量的数据进行拟合，预测。

1）计算相关系数矩阵:

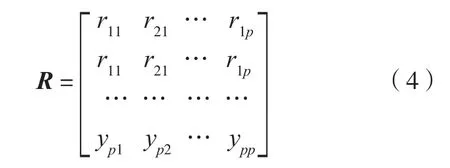
上述公式中yii(i,j=1, 2,…,p)为原来变量xi与xj的相关系数，其计算公式为：

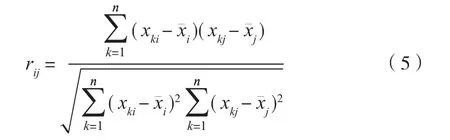
因为R是实对称矩阵（即yij=yji)，所以只需计算其上三角元素或下三角元素即可。

2）计算特征值与特征向量:

首先求解特征方程求 出 特 征 值λi(i=1, 2, …,p)，并使其按大小顺序排列，即λ1≥λ2≥…≥λp≥0；然后分别求出对应于特征值λi的特征向量ei(i=1, 2, … ,p)。

3）计算主成分贡献率及累计贡献率:

主成分Zi贡献率：(i=1, 2, …,p)，累计贡献率：。一般取累计贡献率达85～95%的特征值λi,λ2, …λm所对应的第一，第二，……，第m, （m≤p）个主成分。

4）在MATLAB中，利用选取的主影响因素和因变量的数据进行拟合，预测。

2.2.2 灰色预测

灰色系统GM（1,1）[5]是指现有的系统信息量很小，并且不能完全把握系统内部的联系，整个系统就像一个朦胧的灰色暗箱。但是系统之间的各个信息指标也是有一些潜在的联系的。对于信息量不完备的信息系统来说，均可以利用灰色预测系统进行预测。

由于原始的数据具有随机性，为了寻找灰色系统之间的信息联系，首先我们要消除这种随机性，对灰色信息系统的原始数据做相关的处理，经过数据处理后的时间序列即称为生成列，灰色系统常用的数据处理方式有累加和累减两种。

累加生成数指一次累加生成，记原始序列为：X(0)={x(0)(1),x(0)(2),…x(0)(n)}，一次累加生成序列为：X(1)={x(1)(1),x(1)(2),…x(1)(n)}.其中，

累减生成是累加生成的逆运算。记原始序列为 ：X(1)={x(1)(1),x(1)(2),…x(1)(n)}。 累 减 生 成 序 列为 ：X(0)={x(0)(1),x(0)(2),…x(0)(n)}， 其 中x(0)(k)=x(1)(k)-x(1)(k-1)，规定x(1)(0)=0。

GM（1，1）表示一阶、一个变量的灰色系统模型，令X(0)表示需要建模的序列，X(1)为X(0)的一次累加生成序列，则有，定义Z(1)为X(1)的紧邻均值生成序列：z(1)(k)=(x(1)(k)+x(1)(k-1))/2，可建立如下灰微分方程：x(0)(k)+az(1)(k)=b

记â=(a,b)T,则灰微分方程的最小二乘估计参数满足式（1）：â=(BTB)-1BTYn

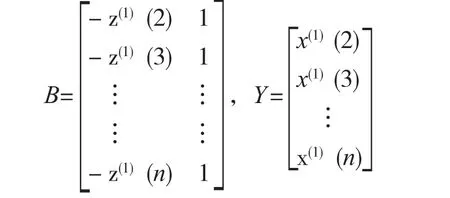
2.2.3 最小二乘法预测

最小二乘法[6]就是使所选取的参数估计值a1′,a2′,…ak′应使变量Y的各观测值yi与其真值的估计值（又叫拟合值）即f(xi:a1,a2,…,ak)之差的平方和最小。

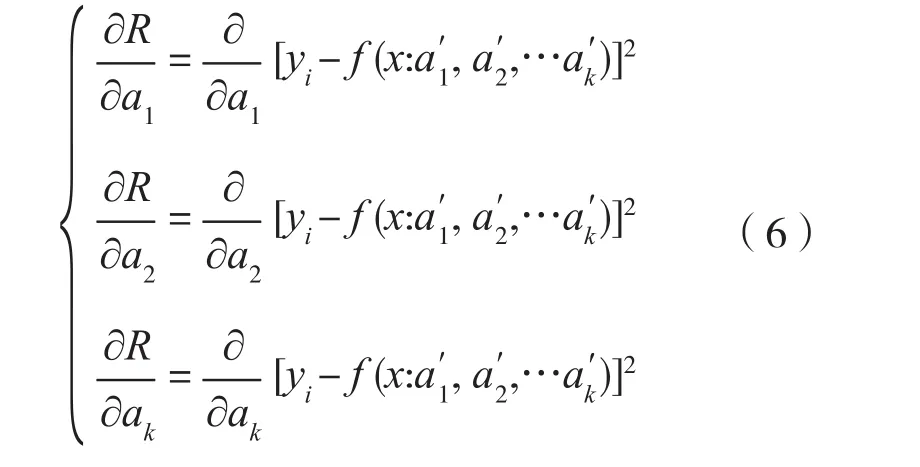
共得k个方程，称为正规方程，求此联立方程的解可得出诸参数的估计值a1′,a2′,…ak′。

2.2.4 组合预测

根据GM（1，1）、最小二乘法预测、主成分回归等方法得到的数值，即各预测方法的百分误差均值所占比例赋予其相应的权重，可得到组合预测的表达式：

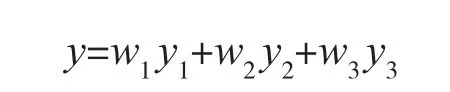
其中y1,y2,y3,分别表示灰色预测、最小二乘法、主成分回归法得到的预测值；w1,w2,w3分别表示灰色预测、最小二乘法、主成分回归法的权重。

2.3 结果分析

首先，通过查找相关资料，在中国统计年鉴上找到了安徽省农田灌溉水利用效率及其影响因素的相关数据如表4：

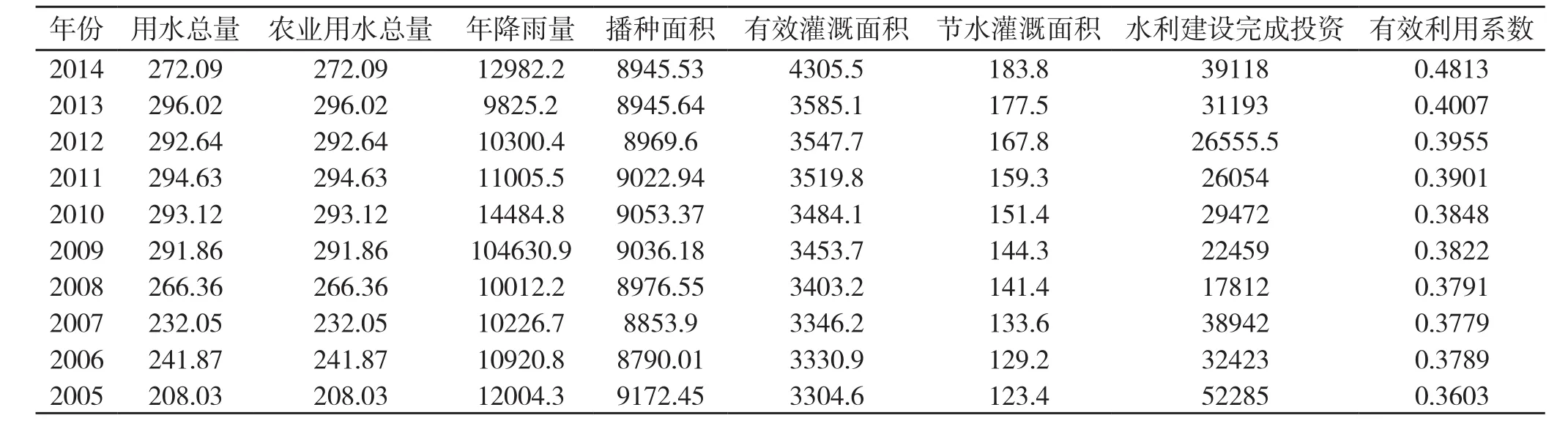
表4 农田灌溉水利用率及其影响因素数据表

2.3.1 主成分分析结果

根据主成分分析的模型，在MATLAB中编程并运行，得到各指标特征根与贡献率如图3、图4：

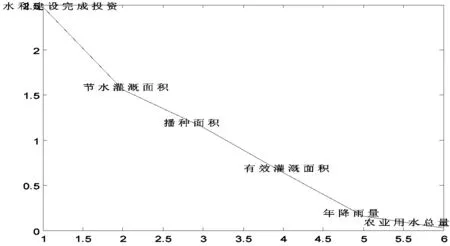
图 3 各个因素变量的特征根

通过主成分分析法得出影响灌溉水有效利用系数的主要因子，水利建设完成投资和节水灌溉面积是影响灌溉水有效利用系数的两大因素，加大对水利建设的投资，增加节水灌溉面积，加强用水管理等都是增大灌溉水有效利用系数的有效途径。

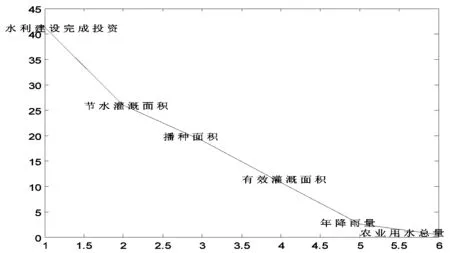
图 4 各个因素变量的贡献率

2.3.2 GM（1，1）、最小二乘法预测、主成分回归预测结果

根据GM（1，1）、最小二乘法预测、主成分回归，在MATLAB中分别求出了GM（1，1）、最小二乘法预测、主成分回归法下的农田灌溉水利用效率的预测值，将主要结果整理在表中，见表5：

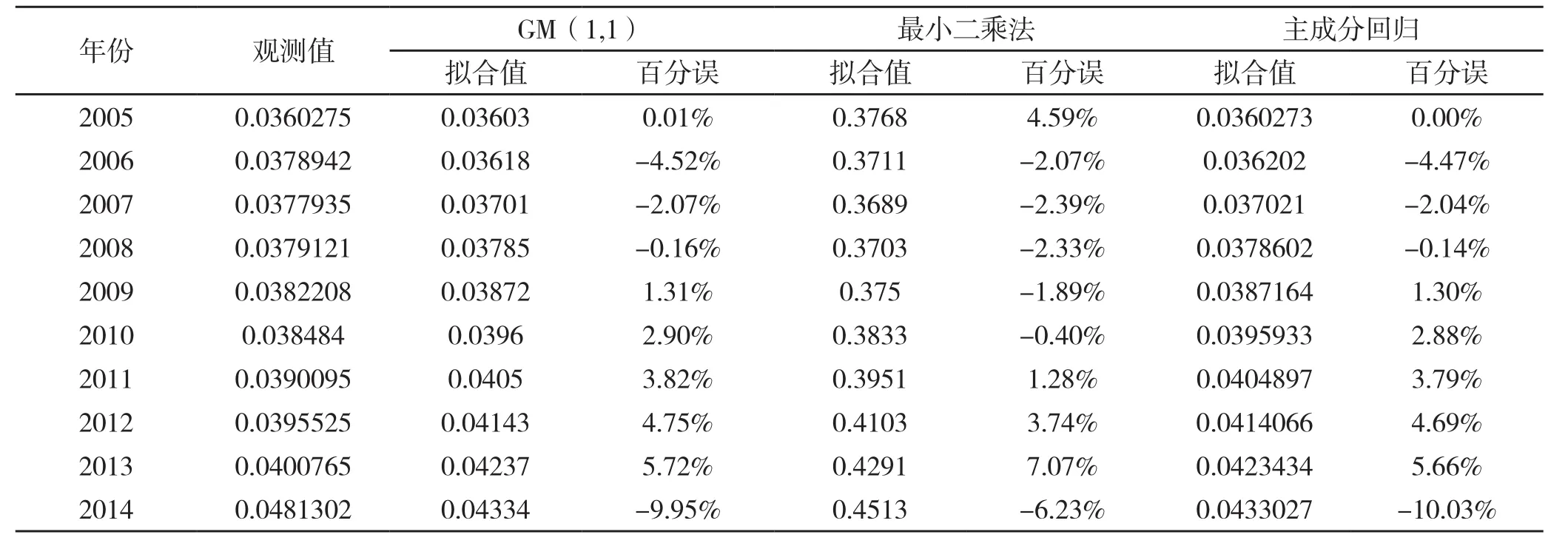
表5 各种预测方法的检验

不同方法的误差曲线图如图5所示：

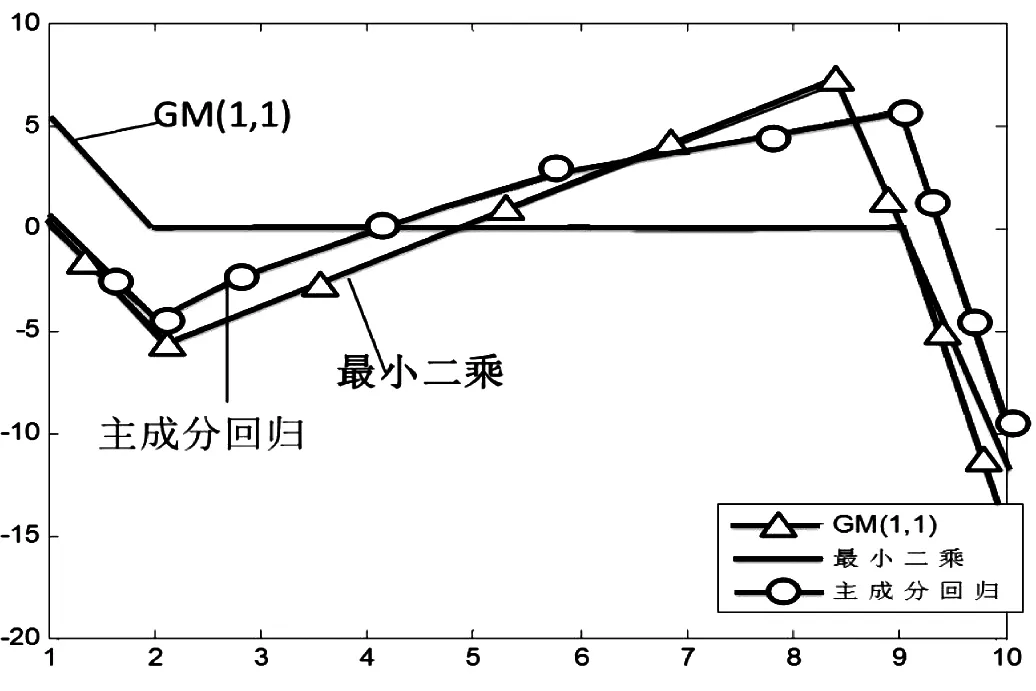
图 5 各方法误差值比较图

2.3.3 求出组合预测值

将GM（1，1）、最小二乘法预测、主成分回归预测的结果代入所建立的组合预测模型可以得出到2020年农田灌溉水利用系数。

表6 2020年预测值

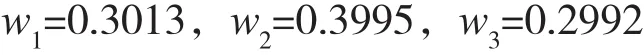
组合预测表达式为：

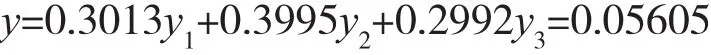
3 相关建议

在未出台“十三五”国家循环经济总发展规划前，就已发布了加快绿色农业循环经济发展的相关指导意见。由此可见中央对发展农业循环经济的重视。这也是为了响应国家的供给侧改革战略。针对强化农业供给侧生产方式创新、进一步推进农业绿色循环发展。本文提出相关建议如下：

3.1 提高化肥利用率，推动无机与有机化肥的结合

3.2 减少农药使用量

开展农药使用量零增长行动，将生物基因技术融入育种中，培育出具有抗病，抗旱，耐寒的高质量种子。这样可以减少农药的使用。此外，还可以通过研发出高精度的喷洒农药作业工具，实现科学喷洒农药。

3.3 扩大农田有效灌溉面积，发展节水灌溉

由前面主成分分析可知有效灌溉面积是影响农田灌溉水利用效率的重要因素之一。因此必须提高灌溉的精准度，不能白白浪费水资源。比如可以提倡农田的集中化处理，实现规模种植，这样在灌溉的时候其利用效率必然会大大增加。此外在灌溉的过程中聘请专业人员来测算最佳的灌溉水量，并控制好灌溉水的速度的和流量。最大化地提高有效的灌溉面积。其次实行管灌，微灌，渠道防渗，坐水种等灌溉方式，都可有效地提高水分的利用效率，发展节水灌溉。

[1] 朱品文.我国绿色循环农业经济发展规模特征，效率评价及优化路径研究[J].农业经济，2016（40：9-11.

[2] 王振友，陈莉娥.多元线性回归统计预测模型的应用[J].与决策，2008（5）：46-47.

[3] 刘彦飞.提高农田水利灌溉效率的重要作用和意义[J].科学与财富，2017（19）：231.

[4] 方健，李自品，彭辉，戴思初，吴晓文.基于主成分分析法的BP神经网络的应用[J].变压器，2011（1）：47-51.

[5] 杨华龙，刘金霞，郑斌.灰色预测GM（1，1）模型的改进及应用[J].数学的实践与认识，2011（23）：39-46.

[6] 邹乐强.最小二乘法原理及其简单应用[J].科技信息，2010（231）：282-283.