Nekrasov矩阵的逆矩阵无穷范数的估计式

李艳艳

（文山学院 数学学院，云南 文山 663009）

Nekrasov矩阵是H矩阵的新子类，1998年黎稳在文献[1]中给出了Nekrasov矩阵的定义，随后关于该矩阵的判定方法，行列式的估计问题在文献[2-4]中得到了广泛的研究，2013年，L.Cvetkovic,P.F.Dai等在文献[5]中研究了该矩阵的逆矩阵无穷范数的界的估计。本文继续研究该问题，通过构造参数可调节的新估计式，提高了上界估计的灵活性和精确度。

1 预备知识

令Cn×n（Rn×n）表示复（实）矩阵的集合，N表示自然数的集合。

设A=(aij)∈Rn×n，若A的比较矩阵可逆，且＜A＞-1≥0，则称＜A＞是M矩阵，同时称A是H矩阵。

设A=(aij)∈Rn×n，若，则称A是严格对角占优矩阵；若|aij|＞hi(A)（h1(A)=r1(A)=则称A是Nekrasov矩阵。

将矩阵A分裂为A=D-L-U，其中D=diag(a11,a22, …ann)，

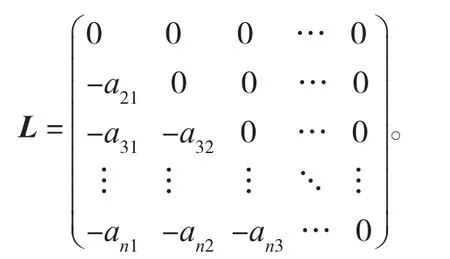
引理 1(Varah 界 )[6]设矩阵A=(aij)∈Rn×n是严格对角占优矩阵，则

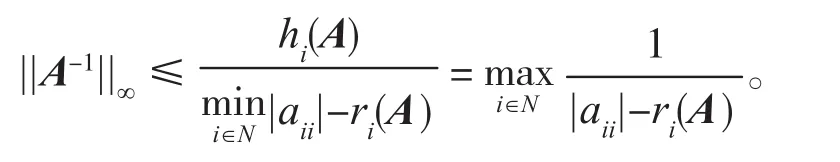
引 理 2[7]矩 阵A=(aij)∈Rn×n，n≥ 2 是 Nekrasov矩阵的充要条件是

(|D|-|L|)-1|U|e＜e，

同时，该条件还隐含了E-(|D|-|L|)-1|U|是严格对角占优矩阵，其中E是单位矩阵。

引理 3[8]设A=(aij)∈Rn×n，是非奇异H矩阵，则

|A-1|≤ ＜A＞-1。

引 理 4[5]设 矩 阵A=(aij)∈Rn×n是 Nekrasov矩 阵，则有

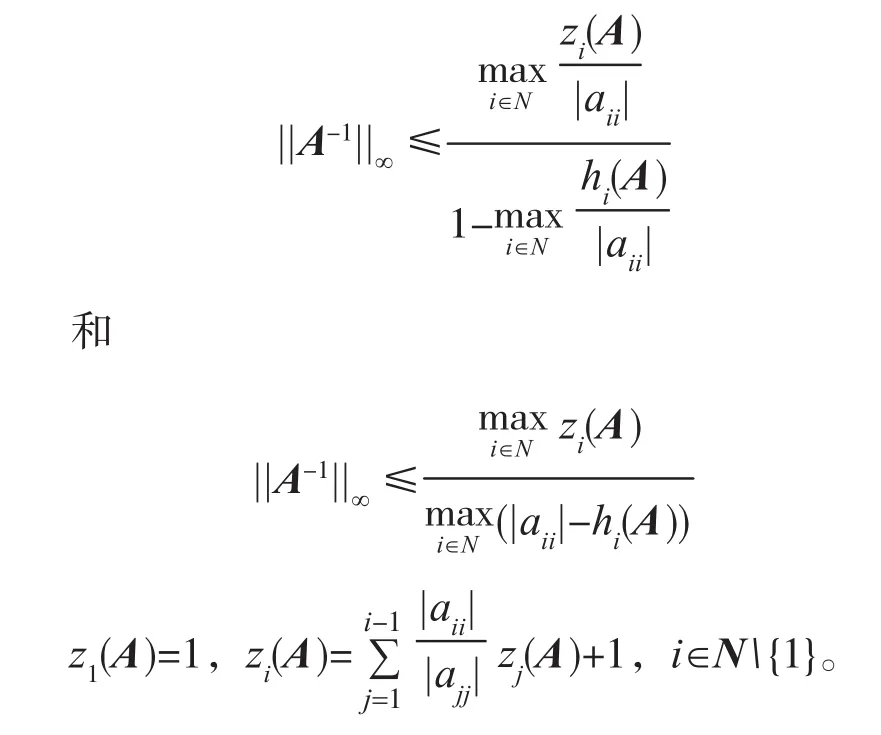
2 Nekrasov矩阵无穷范数的上界

本部分，通过构造参数可调节的新估计式，提高了上界估计的灵活性和精确度。

设A为Nekrasov矩阵，令C=E-(|D|-|L|)-1|U|，B=|D|C，则

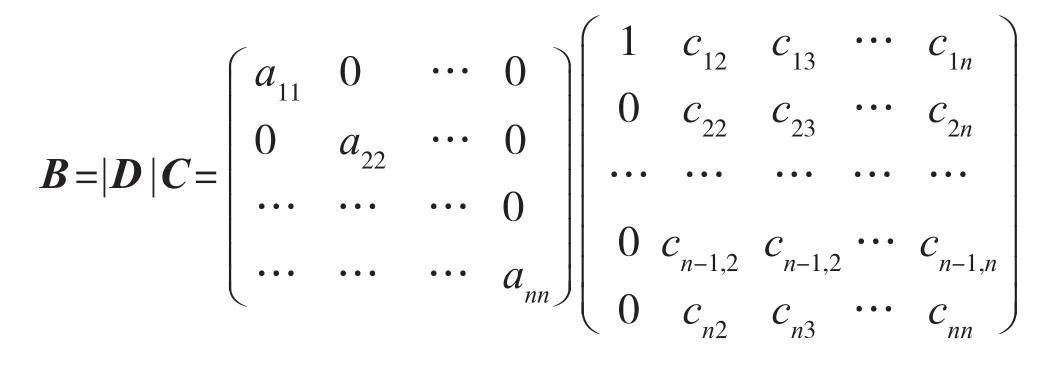
定 理 1 设 矩 阵A=(aij)∈Rn×n是 Nekrasov矩 阵，B=E-(|D|-|L|)-1|U|,B(μ)=BD(μ),

则B(μ)是严格对角占优矩阵且

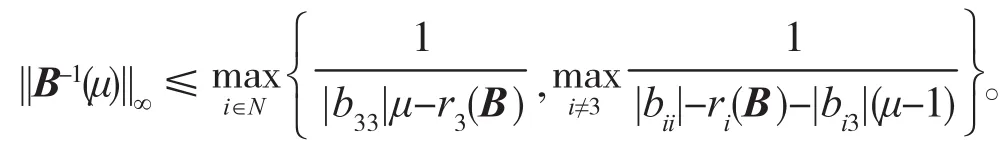
证明：由B(μ)的定义知，B(μ)改变矩阵B的第三列，对其他列没有改变，又由μ的定义知，因为, 则|b33| μ＞r3(B)（第 3 行）

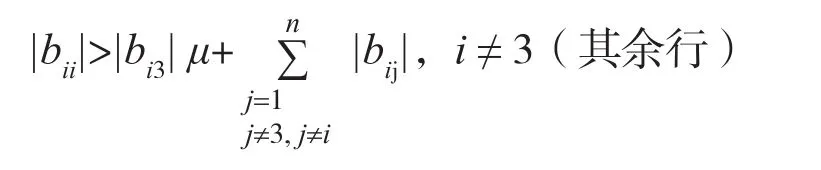
则B(μ)是严格对角占优矩阵。

由引理1的Varah界得

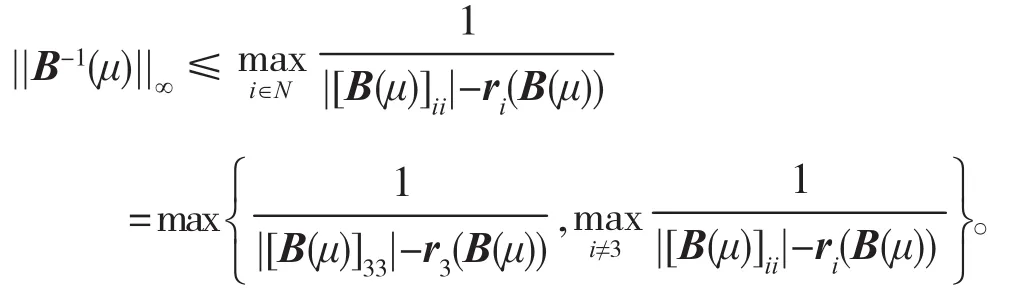
由B(μ)的定义知，[B(μ)]i3=bi3μ，i∈N，[B(μ)]ij=bij，j ≠3，i∈N，

所以 [B(μ)]33=b33μ，r3(B(μ)) =r3(B),

即|[B(μ)]33|-r3(B(μ))=|b33| μ-r3(B)，

对于i∈N，i ≠3 有

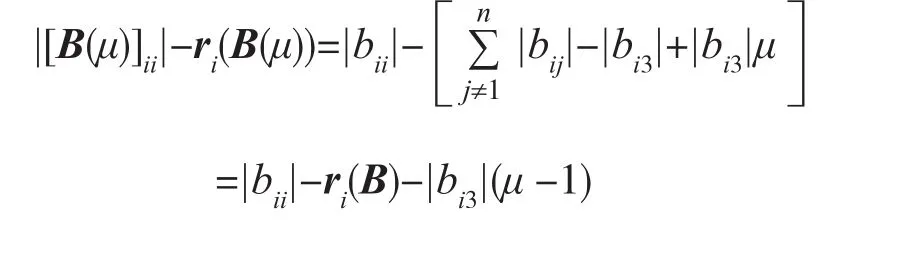
结合以上分析得

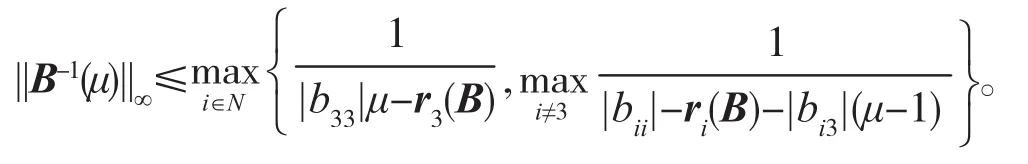
定理 2 设矩阵A=(aij)∈Rn×n是 Nekrasov矩阵，则

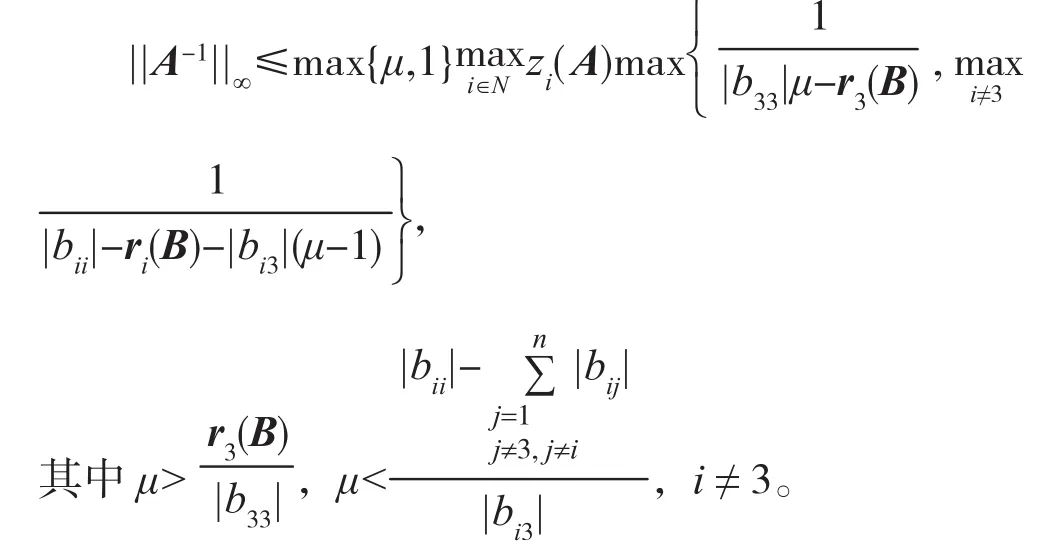
证明：由于矩阵A是Nekrasov矩阵，则由引理2知E-(|D|-|L|)-1|U|，B是严格对角占优矩阵。

由定理1的证明知，B(μ)是严格对角占优矩阵。

因为 ＜A＞=(|D|(|D|-|L|)-1)-1B(μ)D(μ)-1=(E-|L||D|)-1)-1B(μ)D(μ)-1。

所以由引理3知

||A-1||∞≤||＜A＞-1||∞≤||D(μ)||∞||B(μ)-1||∞||(E-|L||D|-1||∞。

由E-|L||D|-1是M矩 阵， 则||(E-|L||D|-1)-1||∞=||(E-|L||D|-1)-1e||∞，

定义z(A)=(E-|L||D|-1)-1e，那么e=(E-|L||D|-1)z(A)，

则z1(A)=1，

即||(E-|L||D|-1)-1||∞=||z(A)||∞=maxi∈N zi(A)。

结合以上分析得

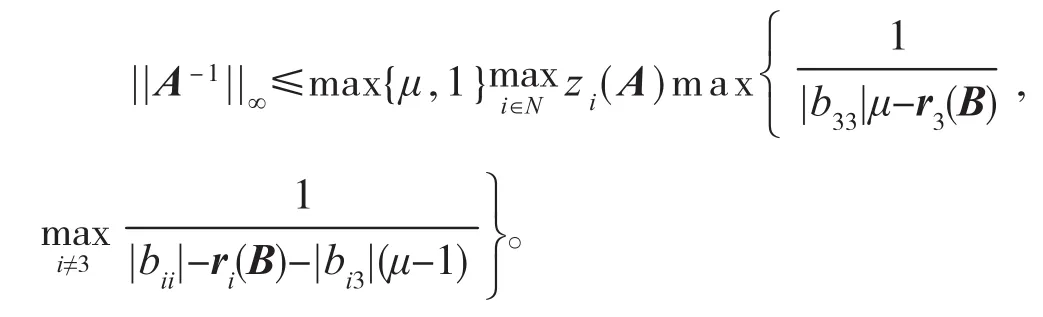
3 数值算例

计算得z1(A)=1,z2(A)=2,z3(A)=1.2971,z4(A)=1.2394;

h1(A)=3.2000，h2(A)=8.2000，h3(A)=2.9609，h4(A)=0.7359;

||A-1||∞=0.1921，由引理 4 知||A-1||∞≤0.5263，应用本文定理 2 当μ=1.2092 时，||A-1||∞=0.1985。

该例说明本文所得估计式的有效性，且一定情况下，优于文献[5]中的估计式。

[1] Li W.On Nekrasov matrices[J].Linear Algebra and Its Applica tion,1998,281:87-96.

[2] 郭爱丽,邓慧琳.广义Nekrasov矩阵的一组充分条件[J].贵州工程应用技术学院学报，2016（2）：139-143.

[3] 苏安兵.Nekrasov矩阵的性质及其判定研究[D].湘潭:湘潭大学，2016.

[4] 郭爱丽,聂祥荣,武玲玲.Nekrasov矩阵行列式界的估计[J].安徽大学学报（自然科学版），2015（6）：15-18.

[5] L.Cvetkovic,P.F.Dai,K.Doroslovacki,etl.Infinity norm bounds for the inverse of Nekrasov matrices[J].Applied Mathematics and Computation,2013,219:5020-5024.

[6] Varah J M. A lower bound for the smallest singular value of a matrix[J].Linear Algebra and Its Application,1975,11:3-5.

[7] SZULC T. Some remarks on a theorem of Gudkov [J]. Linear Algebra and Its Application, 1995, 225:221-235.

[8] BERMAN A, PLEMMONS R J. Nonnegative matrices in the mathematical sciences[J]. Classics in Applied Mathematics,1994, 9:32-40.