求解二次函数几何变换问题的解析
2017-01-26卢彩霞
卢彩霞
(甘肃省兰州市第八十三中学)
求解二次函数几何变换问题的解析
卢彩霞
(甘肃省兰州市第八十三中学)
北师大版对二次函数内容的学习是在一次函数、反比例函数基础上进行的,对它的讨论是从最简单的二次幂函数开始的,研究它的图象和性质,明确函数的三种表示形式,便于从不同侧面对函数性质的觉察和从不同角度的整合中对二次函数形成整体性认识。纵观近几年中考试卷,二次函数的相关知识点经常被作为压轴题在选择题、填空题及解答题中频繁出现,但学生往往容易失分,怎样能够有效得分,利用相关实例结合实践操作多方面解答此题。
二次函数;几何变换;实践操作
以二次函数为背景的几何图形的变换问题是近年来全国各地数学中考的热点题型,因此,备受命题者的青睐。这类试题常常需要用到数形结合思想、转化思想、分类讨论思想等,解决这类问题的关键就是要熟练应用几何图形的变换性质和二次函数的有关知识进行分析、探究,以达到考查学生综合运用知识解决问题的能力。笔者从2016年兰州市中考模拟数学试题中选取第15题,加以解析说明,以飨读者。
A.3 B.3.5 C.4 D.4.5
分析:首先求得平移后的解析式,进而求得顶点A的坐标,通过分析找出满足题目要求的P点及求得坐标,求得P点直线OA的距离,然后根据三角形面积公式即可求得。

图1
解答:方法一:
方法二:
《义务教育数学课程标准》明确指出学生学习应当是一个生动活泼的、主动的和富有个性的过程。学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。动手实践也是一种学习数学的重要方式之一。因此,通过实践操作本题还有如下解法:
分析:方法一是根据平行线间垂线段最短,找到点P的位置从而满足△POA的面积最小。现在如果换个思路,如果能在抛物线C2上找到一点到线段OA的距离最短,那么问题就迎刃而解了。
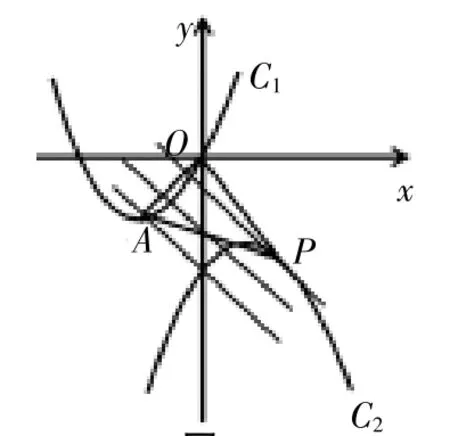
图2

●编辑 温雪莲
