基于空间均匀网格的光子映射算法研究

王海波+陈中+朱喜基+周华先

摘 要：光子映射是一种全局光照方法，在渲染辉映、焦散、漫反射等方面效果良好。通常的方法是发射光子，建立基于K-D tree的光子图，然后在此基础上寻找与估算点相应的光子完成光辐射强度估算，最后渲染图形，具有生成图形慢、内存消耗大等缺点。鉴于此，提出一种新方法：先建立空间均匀网格，发射光子后，再利用GPU的并行功能建立光子与网格映射关系偏移表，之后寻找估算点的光子完成光辐射强度估算，渲染图形。实验结果表明，新算法生成的图形速度更快、更清晰，具有更高的实用价值。

关键词：光子映射；均匀网格；GPU；偏移表

DOIDOI：10.11907/rjdk.162461

中图分类号：TP311

文献标识码：A文章编号：1672-7800（2016）012-0019-03

0 引言

光子映射是全局光照算法，通常先从光源向场景发射光子，建立基于K-D tree的光子图，接着从光子图中寻找估算点的光子完成对估算点光辐射强度估算，最后生成图形[1]。光子映射的光子图与场景表述可以分离，光子映射能处理很复杂的场景，包括千万个三角面片、实例化的几何体、复杂的过程式物体[2]。

针对通常算法消耗内存大、生成图形慢的缺点，Per H Christensen[3]于2002年提出凸多边形的思路，该方法是获取一组离估算点最近的光子，再求出包围光子的最小凸多边形，进而利用凸边形的面积作为估算光辐射强度估算时的分母。该方法能比较精确地估算光辐射强度，但耗时很长。同年Heinrich Hey[4]提出另一种精确估算光辐射强度的算法。该算法的思想是：场景中的每个物体都用网格表示出来，采用立方体收集光子，并求出每个立方体内的多边形面积，每个光子的能量平均分配到光子正对着的多边形，每个多边形的光辐射能应与沿着光子入射方向的投影面积成正比。2005年Szbolcs Czuczou[5]应用图形硬件的纹理结构存储光子，用滤波方式搜索最邻近的光子信息，该方法的好处是可以一步获取所有顶点的辐射能，缺点是获取的辐射能仅是平均值。2008年Hachisuka等[6]采用逐步缩小估算半径，同时采用加大光子密度的办法，在渲染水面焦散时效果较好。2009年Dan A.Alcantara[7]等在GPU上实现光子的哈希并行算法，搜索有效光子的速度更快，但需开辟较大的共享内存。耿中元、徐庆为[8]为了改善物体细节部分的绘制效果，2009 年提出对搜索范围内的每个光子都求出它在绘制点上的切平面投影，通过判断投影点与绘制点之间的距离是否小于搜索半径，进而决定是否使用该光子计算光辐射强度。2011年Wojciech Jarosz[9]等提出采用自适应光子束方法渲染有参与介质的柱状型光照时取得较好效果。2012年Doidge[10]结合渐进光子映射算法与路径跟踪算法的优点，在渲染焦散现象时采取光子映射算法，渲染其它现象时则采用光线跟踪算法，两种算法互相切换的花费较大。2013年Ben Spencer[11]等先为每个光子划分一个沃罗诺伊空间，接着采用渐进光子的方式计算光辐射强度。2013年Mara、Luebke、McGuire[12]利用GPU的栅格硬件，在对光辐射强度估算时采用多面体方法获取光子，提高了光辐射强度的精度，先从理论上证明该方法的一致性，实验上也验证了该算法的有效性，但该算法在处理较复杂的场景时会对估算点重复计算。

新算法先将物理空间分成均匀网格，然后发射光子，再建立均匀网格与光子的映射关系偏移表，实验结果比通常基于K-D tree的光子映射算法更快，图像也更清晰。

1 网格算法

Step1：空间均匀网格建立。先将场景分为可与图形像素一样多的包围盒[13-14]，之后再根据统一的尺寸划分网格，一般网格以搜索半径r[15]为长度。划分网格时间只占整个网格构建的一小部分时间。

Step2：为每个光子计算索引。网格建好后需要为每个光子分配光子索引可采用如下方式分配索引：

Idx（p）=G（p）.x+G（P）.y.GridSize.x+G（p）.Z.GridSize.x.GridSize.y（1）

其中，G（p）=[（p-worldOrigo）/cellSize]。GridSizex表示x轴上的网格数，GridSizey表示y轴上的网格数，GridSizez表示z轴上的网格数。索引值的范围为0～N，其中N=GridSizex.GridSizey.GridSizez.所有的光子都分配到0～N-1中去，由于这部分可以并行进行，采用GPU的kuda作并行计算[16-17]。

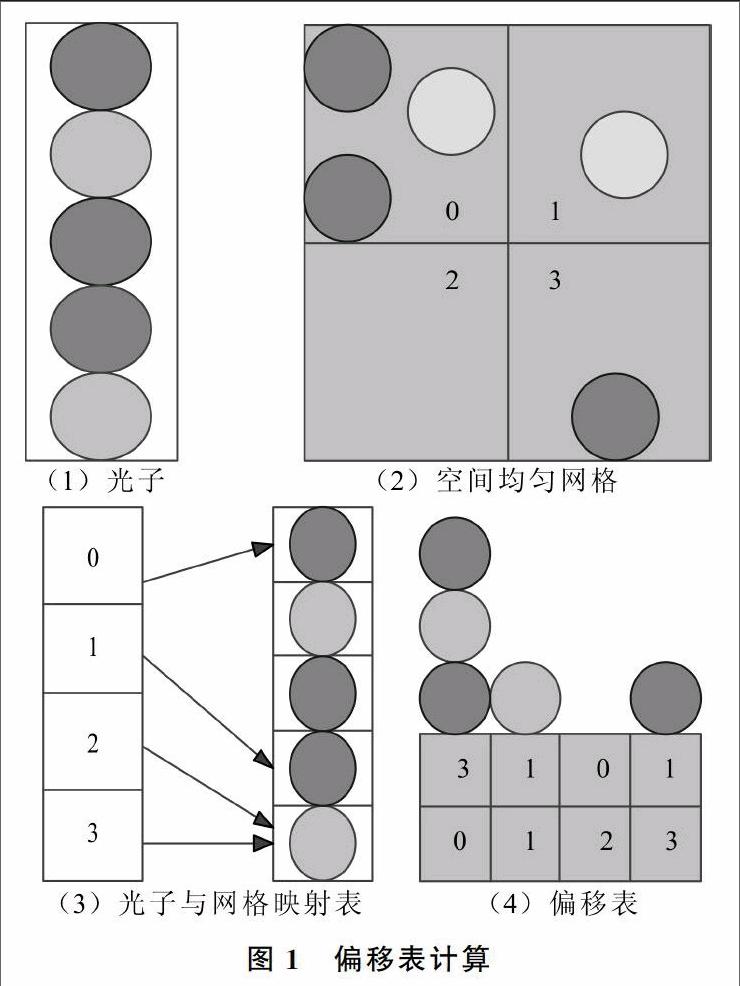
Step3：偏移表（Offset Table）计算。完成均匀网格划分、光子存储、光子与网格对应关系建立，再建光子偏移表，用于光子搜索，如图1所示。

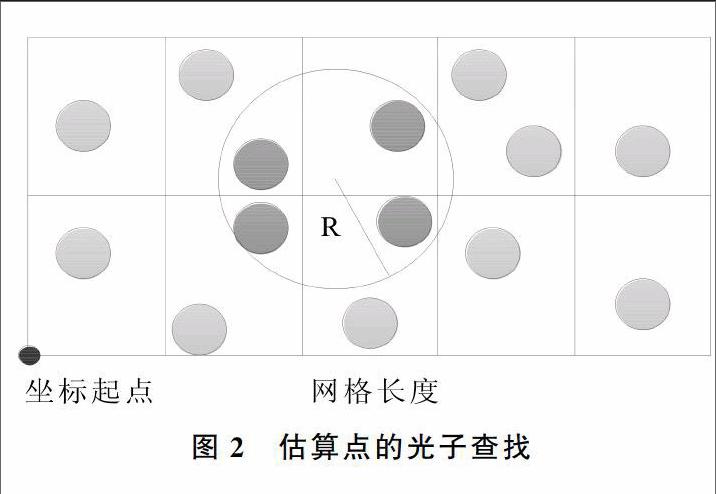
Step4：利用均匀网格寻找光子。利用存储光子的数组和偏移表，查找估算点的光子，如图2所示，需要寻找到所有符合要求的光子。先找到估算点要达到的最小网格和最大网格，如在x轴的最小网格和最大网格半径内，如果网格空间的大小正好等于搜寻半径，则在立体空间中最多需要搜寻8个网格，可用GPU的kuda并行搜寻。算法描述如下：

xMin=Max（0，[p.x-worldOrigo.x-radius]/cellSize）]

xMax=Min（GridSize.x-1，[p.x-worldOrigo.x-radius]/cellSize）]）

normPosition ：p-worldOrigo；

xMin：=max（0，floor（normPosition.x-R）/cellSize）

xmax：=min（GridSize.x-1，floor（normPosition.x+R）/cellSize）；

yMin：=max（0，floor（normPosition.y-R）/cellSize）；

yMax：=min（GridSize.y-1，floor（normPosition.x+R）/cellSize）；

zMin：=max（0，floor（normPosition.z-R）/cellSize）

zMax：=min（GridSize.z-1，floor（normPosition.z+R）/cellSize）；

getHashValue（x，y，z）{

return x+y*gridSize.x+z*gridSize.x*gridSize.y；}

If（xMin<=xMax）{

For（y：=yMin； y <=yMax； y++）{

For（z：=zMin； z<=zMax； z++）{ hashFrom：=getHashValue（xMin，y，z）； hashTo；=hashFrom+（xMax-xMin）； offsetFrom：=offsetTable[hashFrom]； offsetTo：=offsetTable[hashTo+1]；

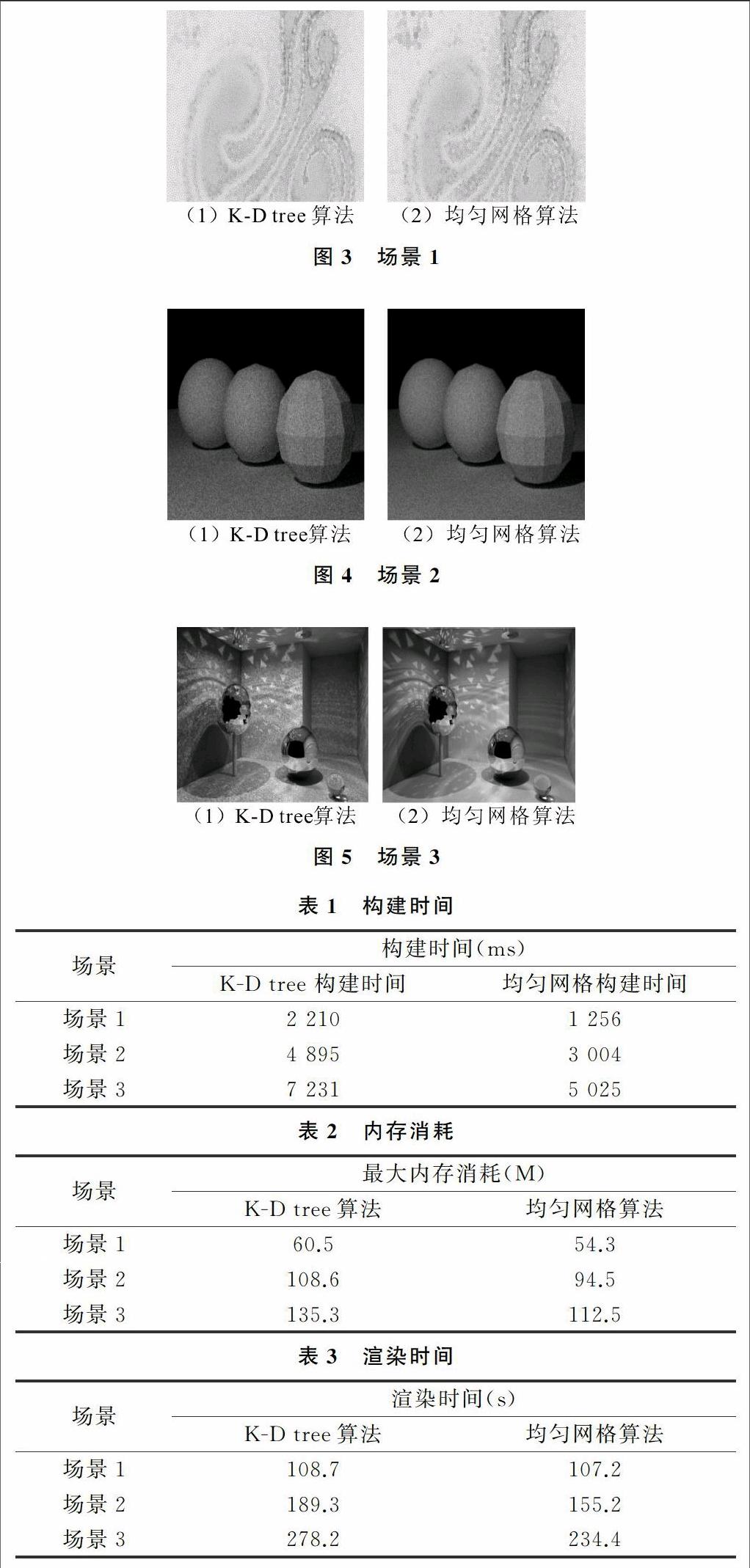
for（i：=offsetFrom； i

photon：=photons[i]；

if（length（photon.position-p）<=R）{

Accumulate power of photon i

}

}

}

}

}

2 结果分析

实验条件：系统Win7，处理器Intel I5处理器2.5G，内存8G，Geforce 610，使用C++GL渲染图形。在网格划分好后，使用GPU的cuda技术，场景1为像素640×480，发射的光子数为50 000个；场景2像素为1 366×768，发射的光子数为100 000；场景3像素1 366×768，发射的光子数为200 000个。从图形清晰度来看，网格算法的清晰度比K-D tree算法清晰度更高，原因是网格算法建立光子的映射关系更精准。从表1、表2、表3可以看出，在各场景中网格的构建时间比kd树的构建时间都快，最大内存消耗网格算法比K-D tree算法低，在总的渲染时间上，网格算法比K-D tree算法低。

3 结语

新的算法是先将空间划分成均匀网格，发射光子后，再利用GPU的并行功能建立光子与网格映射光子，最后利用该映射关系来查找估算点的光子，进而渲染图形。在以后的研究中可以更多地利用GPU并行功能加速图形的生成，并进一步优化光子与网格的映射。

参考文献：

[1] H W Jensen.Global illumination using photon maps，proceedings of the seventh eurographics workshop on rendering1996[C].Switzerland：Aire-la-Ville，1996：19-26.

[2] HEINRICH HEY，WERNER PURGATHOFER.Advanced radiance estimation for photon map global illumination proceeding of eurographics，2002[C].Switzerland：Eurographics，2002：541-545.

[3] WOJCIECH JAROSZ，HENRIK W JENSEN.Advanced global illumination using photon mapping[C].USA：Siggraph，2008：65-70.

[4] HEINRICH HEY，WERNER PURGATHOFER.Advanced radiance estimation for photon map global illumination，proceeding of eurographics[C].Switzerland：Eurographics，2002：541-545.

[5] SZABOLCS CZUCZOR，LáSZló SZIRMAY-KALOS，LáSZló NEUMANN.Photon map gathering on the GPU[C].Spanish-Hungarian：EUROGRAPHICS，2005：143-152.

[6] WOJCIECH JAROSZ，HENRIK W JENSEN.Advanced global illumination using photon mapping[C].USA：Siggraph，2008：65-70.

[7] DAN A ALCANTARA，ANDREI SHARF.Real-time parallel hashing on the GPU[C].Asia：Proceedings of ACM SIGGRAPH，2009：243-252.

[8] 耿中元，徐庆，孙济洲.改进的光辐射强度估算[J].系统仿真学报，2009（14）：4471-4474.

[9] WOJCIECH JAROSZ，DEREK NOWROUZEZAHRAI，ROBERT THOMAS.Progressive photon beams[C].NY：Proceedings of ACM SIGGRAPH Asia，2011：546-555.

[10] IAN C，DOIDGE MARK W，JONES，et al.Monte carlo and progressive rendering for improved global illumination[J].The Visual Computer June，2012（28）：603-612.

[11] BEN SPENCER，MARK W.JONES.Progressive photon relaxation[J].ACM Transactions on Graphics，2013（32）：562-570.

[12] MICHAEL MARA，DAVID LUEBKE， MORGAN MCGUIRE.Toward practical real-time photon mapping：efficient GPU density estimation[C].New York：ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games，2013：71-78.

[13] JEFFREY J.Automatic creation of object hierarchies for ray tracing[J].IEEE Computer Graphics and Applications，1987（5）：14-20.

[14] C GILLES，LBERNARD.Coupled use of BSP and BVH trees in order to exploit ray bundle performance[C].NewYork：IEEE/EG Symposium on Interactive Ray Tracing，2007：231-240.

[15] V GARCIA，E DEBREUVE，M BARLAUD.Fast k nearest neighbor search using GPU[C].Anchorage：CVPR Workshop on Computer Vision on GPU，2008：567-575.

[16] NVIDIA CORPORATION.CUDA ToolKit homepage[EB/OL].https：//developer.nvidia.com/cuda-toolkit.

[17] R FARBER.CUDA Application design and development：applications of GPU computing series[M].San Francisco：Morgan Kaufmann，2011：245-253.

（责任编辑：孙 娟）