基于开关电容和耦合电感的交错并联型高电压增益双向DC-DC变换器

薛利坤王 萍王议锋闫海云张启亮

（1. 天津大学智能电网教育部重点实验室 天津 300072 2. 国网济宁供电公司 济宁 272200）

基于开关电容和耦合电感的交错并联型高电压增益双向DC-DC变换器

薛利坤1王 萍1王议锋1闫海云1张启亮2

（1. 天津大学智能电网教育部重点实验室 天津 300072 2. 国网济宁供电公司 济宁 272200）

提出一种基于开关电容和耦合电感的交错并联型高电压增益双向DC-DC变换器。通过并联通道数的增加，使得变换器具有更高的电压增益、更大的输出功率和更小的器件电压/电流应力。通过引入耦合电感，不仅降低了通道内电流纹波，同时可使各通道的电感量最小，进一步提升变换器的效率和功率密度。而且，较小的电感量可加快开关电容自动均流速度，仅需简单的控制方法，有利于提高电路的可靠性和实用性。制作了一台500W样机，以验证该拓扑和理论分析的有效性。

双向DC-DC变换器 储能 开关电容 耦合电感 交错并联 高电压增益

0 引言

分布式储能装置在交直流微电网和分布式可再生能源并网发电系统中扮演至关重要的角色，为了解决储能装置并联时的低电压和并网所需高电压之间的电压水平不匹配问题，需要用到高增益型双向DC-DC储能变换器[1-3]。近年来提出的多种高升压比电路拓扑可分为隔离型和非隔离型两类，非隔离型高增益双向变换器主要包括开关电容拓扑、开关电感拓扑、耦合电感拓扑和基于电容-二极管的倍压拓扑等[1-7]。其中，开关电容变换器由于具有重量轻、功率密度高等优点而被广泛采用[4-6]。然而，开关电容充、放电过程中各功率器件上存在较大的电流冲击[1]。为了解决此问题，文献[6,8]提出了一类升压型开关电容谐振变换器。文献[9]则提出了一种基于开关电容的双向谐振变换器。上述谐振型开关电容拓扑，可以实现高电压增益和较高效率，但是，极大的输入电流纹波和较为复杂的电路结构，使得这些拓扑仅适用于小功率应用场合。耦合电感变换器往往具有电路结构简单、所需开关器件较少、电路增益可灵活调节等特点[2]，但与谐振型开关电容拓扑一样，仍具有较大输入电流纹波，较难满足大功率应用的需要。

为了减小输入电流纹波和开关器件的电压应力，文献[10]提出了一种带开关电容网络的两相交错并联型高增益Boost变换器，并对其工作原理和各功率开关器件电压应力进行了分析。在此基础上，文献[11]提出了一种基于开关电容的两相交错并联双向变换器，能够减小输入电流纹波和开关器件电压应力，并实现能量的双向流动。但较大的电感量和输入、输出滤波电容导致其自动均流的动态特性较差，变换器易出现电流尖峰甚至失稳，另外其升压、降压模式下最高效率仅为91%和90%。

本文在上述研究的基础上提出一种基于开关电容和耦合电感的4相交错并联双向变换器拓扑。目标是进一步提高双向变换器的效率和功率密度，减小功率器件电压、电流应力以及进一步提高变换器电压增益，最终使其满足较大功率分布式储能充、放电需求。该变换器拓扑如图1所示，1、3相和2、4相的PWM驱动信号分别相同，1、2相和3、4相分别共用一个匝比为1∶1的耦合电感，不考虑电感耦合作用，假设各相电感量相同L1=L2=L3=L4=L。电路利用开关电容C1、C2、C3及CH实现高增益的升压、降压功能，各开关管的最大电压应力约为VH/2。

图1 所提出的高增益双向直流变换器拓扑Fig.1 The proposed high gain bidirectional DC converter

电路工作在电感电流连续模式（Current Continuous Mode，CCM）升压时，能量从VL流向VH，为了避免所有开关管关断时所产生的通道内环流，S1～S4门极驱动信号的占空比D1＞0.5，此时Q1～Q4工作在同步整流状态以进一步提高变换效率。相应地，当电路工作在降压模式时，能量从VH流向VL，此时Q1～Q4门极驱动信号占空比D2＜0.5，而S1～S4将工作在同步整流状态。

上述占空比D1和D2互补的特性，使得该变换器在升压和降压模式下各开关管占空比的工作范围不变，从而可以采用简单而统一的PWM控制方法，有利于变换器的推广和应用。

1 电路模态分析

1.1 CCM升压模式

当电路工作在开关电容充电CCM升压模式时，其主要工作波形和模态划分如图2所示。

图2 CCM升压模式时的工作波形Fig.2 The operating waveforms for CCM step up mode

模态1（t0～t1）：S1、S3导通，S2、S4关断。L1、L3由低压侧电源VL充电，电感电流iL1、iL3线性上升。L2和C1释放能量给C2充电。L2两端电压为VL+VC1-VC2。L4和C3则释放能量给CH充电，L4两端电压为VL+VC3-VH。iL2、iL4线性下降。对应的电压方程如下

C1、C3放电，iC1= -iL2，iC3= -iL4。C2、CH充电，iC2=iL2，iCH=iL4。

由于电容相对较大，而充放电时间很短，所以假设C1、C2和C3上电压在一个周期内为恒定值，即vC1(t)≡VC1，vC2(t)≡VC2，vC3(t)≡VC3。

模态2（t1～t2）：此时，S1～S4导通，L1～L4由VL充电，iL1～iL4线性上升。对应的电感电压方程为

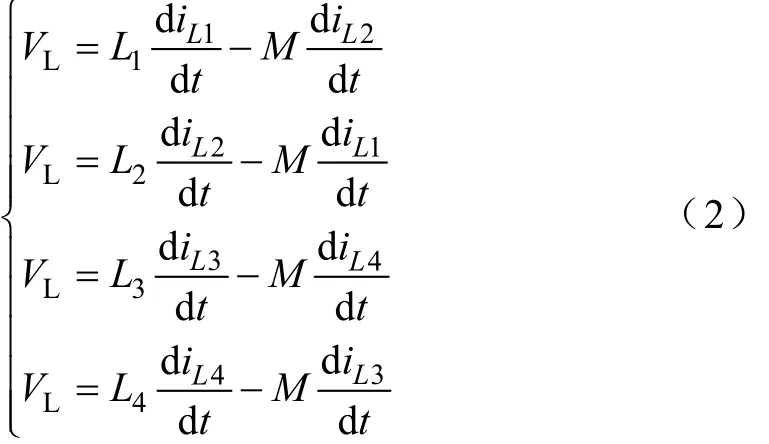
Q1～Q4因承受反向压降而自然关断，开关电容上电流为0，电压恒定。负载由CH供电，其中，VVDQ4=VH-VC3。

模态3（t2～t3）：S1、S3关断，S2、S4导通。L2、L4由VL通过S2、S4充电，iL2、iL4线性上升。L1通过Q1释放能量给C1充电，L1两端电压为VL-VC1。L3与C2，以及低压侧能量源VL串联，通过Q3共同给C3充电，L3、C2释放能量。L3两端电压为VL+VC2-VC3。iL1、iL3线性下降。相应电感的电压方程式为

C1、C3充电，iC1=iL1，iC3=iL3；C2放电，iC2=-iL3。Q2、Q4因承受反向压降而截止，负载由高压侧滤波电容CH提供能量。

模态4（t3～t4）：此时，电路工作状态与模态2相同，S1～S4导通。L1～L4由VL充电，iL1～iL4线性上升。电压方程式同式（2）。

1.2 DCM升压模式

如图3所示为电感电流断续模式（Discontinuous Current Mode，DCM）在升压模式下变换器的主要波形。一个工作周期可分为以下6个模态。

图3 DCM升压模式时的工作波形Fig.3 The operating waveforms for DCM step up mode

模态1（t0～t1）：S1、S3导通，S2、S4关断。L1、L3由低压侧电源VL充电，iL1、iL3线性上升。L2、C1释放能量给C2充电，L4、C3则释放能量给CH充电。iL2、iL4线性下降，在t=t1时刻，下降为0。此时Q2、Q4自然关断，对应的电压方程同式（1）。

模态2（t1～t2）：开关管状态不变，即S1、S3导通，S2、S4关断。L1、L3由VL充电，电流iL1、iL3线性上升。与CCM不同的是，此时C2放电电流为0，S2、S4的输出寄生电容与通道电感谐振，iL2、iL4先负向增加后负向减小，其负向峰值大小与MOSFET输出等效电容有关。

模态3（t2～t3）：S1～S4均导通，L1～L4由VL充电，iL1～iL4线性上升，对应的电感电压方程同式（2）。

模态4（t3～t4）：S1、S3关断，S2、S4导通。L2、L4由VL通过S2、S4充电，L1通过Q1释放能量给C1充电，L3、C2以及VL串联，通过Q3共同给C3充电。iL1、iL3线性下降。相应电感的电压方程式同式（3）。

模态5（t4～t5）：开关管状态不变，即S2、S4导通，S1、S3关断，iL2、iL4线性上升。与模态2相似，由于此时C1、C3放电电流为0，S1、S3的输出寄生电容与通道电感谐振，iL1、iL3呈负向半正弦波形。

模态6（t5～t6）：电路工作状态与模态3相同。S1～S4导通，L1～L4由VL充电，iL1～iL4线性上升。

综上可以看出，与传统Boost电路类似，当电感电流断续时，回路电感与MOSFET输出等效电容将产生谐振。DCM下，只需在电感电流负向减小至0附近（见t1～t2或者t4～t5阶段）开通对应的MOSFET，则可实现软开关的零电压开通（Zero Voltage Switching，ZVS）。

2 电路特性分析

根据上述分析，结合式（1）～式（3），可以分别得到L1～L4伏秒平衡方程式为

由上述方程式组可得到4相交错并联拓扑在CCM升压模式时的电压增益为

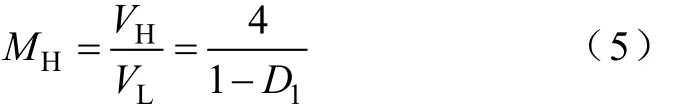
并且

类似地，可以得到该电路在CCM降压模式下的电压增益为

根据以上分析，C1的充电电流等于L1的放电电流，而C1放电电流等于L2的放电电流，利用C1的安秒平衡原理得到L1的放电电流等于L2的放电电流，可见电路第1相和第2相电流平均值相同。C2、C3具有相同的平衡电感电流的能力，因此，开关电容的存在使得该电路具有自动电流均衡能力。

由于开关电容的安秒平衡作用，该电路具有自动电流均衡能力，但该自动调节过程跟电流波动量、变化率及电感量有关，不合适的电感量和控制方法易导致变换器发生振荡而失稳。为了减少自动均流调节所造成的电流波动和调节时间，理论上要求电感量尽可能小，然而较小的电感量将导致通道内电流纹波的增加，本文利用耦合电感和薄膜电容来解决上述矛盾，即采用较小的电感量和较大容量的开关电容以增加系统稳定性。其中，采用反向耦合的耦合电感可以在相同的电感电流纹波前提下减小所需电感量。而薄膜电容具有极低的等效串联电阻、较大电容量、较高耐压、可流通较大高频纹波电流以及无极性等特点，因此非常适用于开关电容的应用场合。本文利用薄膜电容来稳定开关电容和输入、输出电容电压，消除因电感电流振荡引起的电容电压剧烈变化，进而提高变换器的稳定性。

由图2可知，电感电流纹波等于模态3时间段内电感L1的电流增量，该电流变化量跟该时间段内等效电感量成反比关系。因此，在相同的电感L和不同耦合系数k的条件下，要使得电感纹波电流最小，只需要等效电感量取得最大值。

由模态3得到L1、L2的电压方程式为

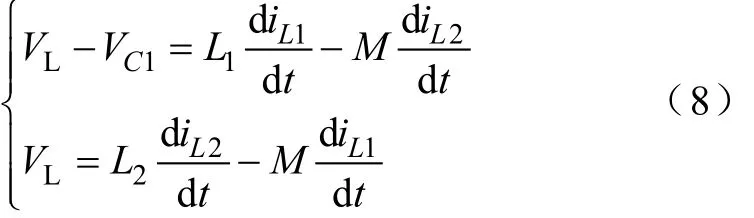
式中，L1=L2=L3=L4=L。

结合式（6）和式（8）可得在模态3时间段内，经过解耦之后通道1的等效电感为

式中，M为互感，M=kL。

在CCM升压模式下，Leq1、D1、L和k之间的相互关系为

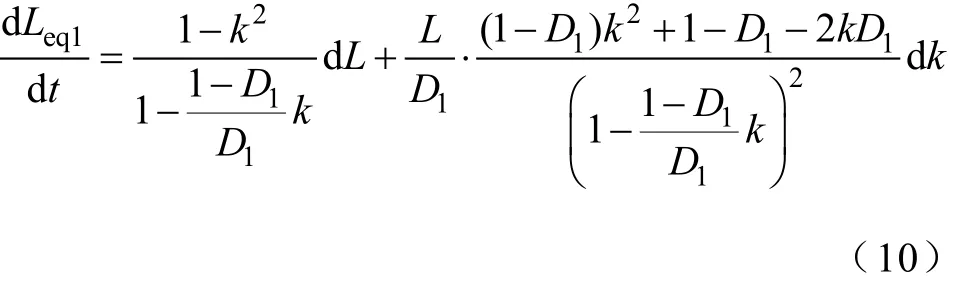
式中，各耦合电感具有相同的k；当等效电感量Leq1取得最大值时

同理，可得到CCM降压模式下等效电感量最大时的耦合系数k为

3 电路参数设计

利用上述理论分析方法可实现电感量L及耦合系数k的优化选取。利用式（10）～式（12）可得到如图4所示的CCM升压、降压模式下耦合系数、占空比和等效电感之间的三维关系。其中不同的电感对应不同的曲面，电感越大则对应的等效电感也越大，每个曲面上的黑色曲线是由相同的占空比D和不同的耦合系数k所对应的等效电感量最大值组成。额定工作点对应的等效电感最大值则用点来标示。

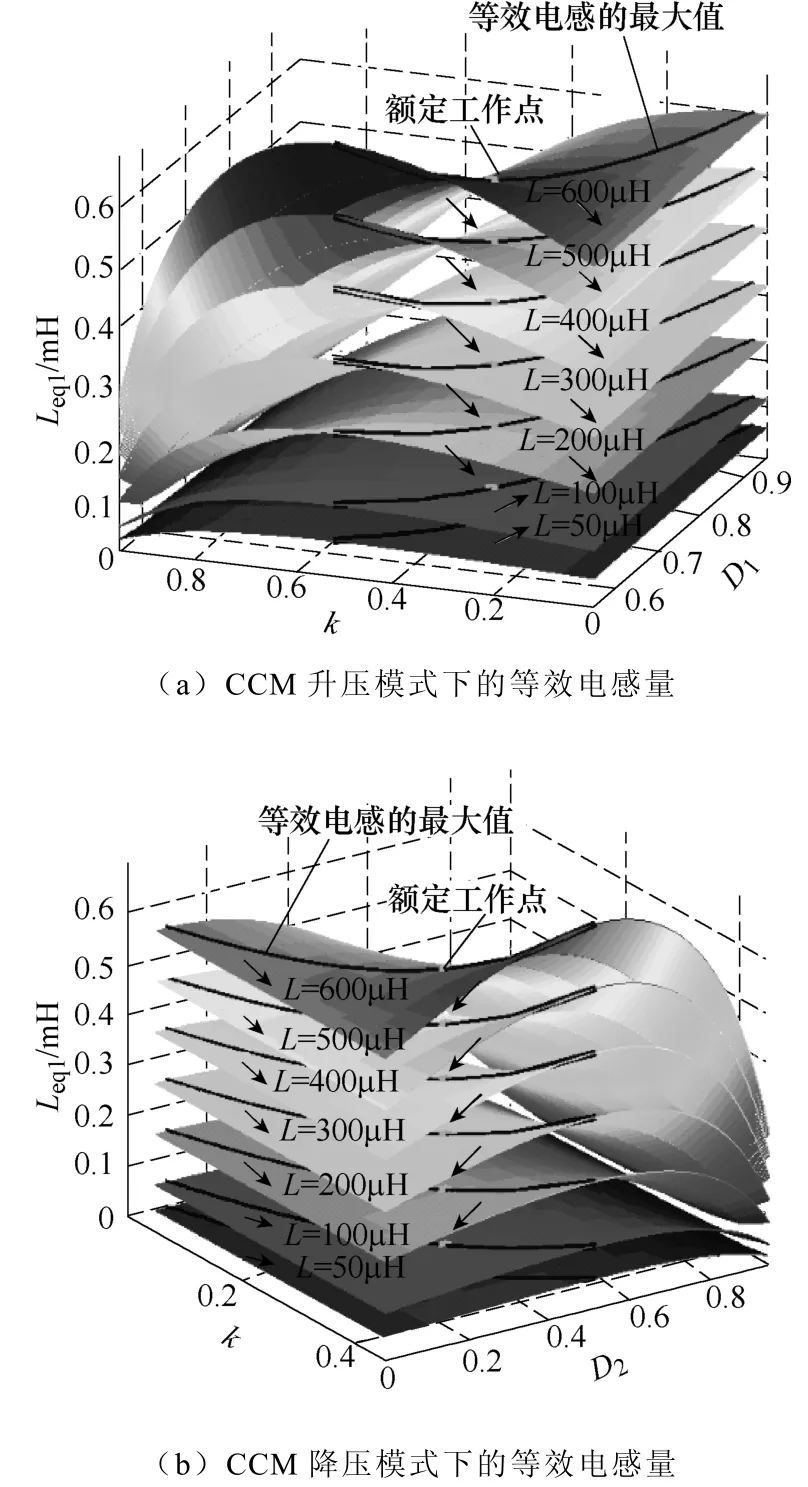
图4 等效电感量与耦合系数及占空比的关系Fig.4 The relationship of equivalent inductor, coupled ratio and duty cycle

从图4可以看出，电感越小，全负载和输入、输出电压范围内的电流纹波变化越小。当各通道电感量L较小时，等效电感量随占空比和耦合系数变化时的波动较小，因此，有利于获得较好的输入电流纹波特性和参数鲁棒性。同时如前文所述，较小的电感量有利于加快自动均流过程的动态调节速度。另外，较小的电感量有利于进一步降低电感体积，提高变换器功率密度，为此本文选择电感在100～150μH范围内。根据理论分析，通道内等效电感量越大则输入电流纹波越小，从图4可以看出，升压和降压模式下耦合系数k≈0.3时，额定输入、输出条件下（此时D1=0.67或者D2=0.33），升压和降压模式均可获得对应L下的最大等效电感量。

因此本文将采用电感量在100μH左右、耦合系数约0.3的耦合电感，目标是在保证输入电流纹波小于1A的前提下，尽量减小电感体积和铜损。

4 实验

根据设定条件：VL=24～48V，VL额定输入36V，VH=400V，Po=500W。优化后的主要电路实验参数见表1。

根据表1中的电路参数，实验室制作了一台500W样机，功率器件S1～S4和Q1～Q4采用SiC MOSFET：C2M0080120D。实验波形如图5～图7所示，额定负载下的实验波形和数据采用300Ω（升压）和1.8Ω（降压）等效电阻测得，轻载波形则为3kΩ电阻。

表1 实验参数Tab.1 The parameters of experiment

图5a～图5c为CCM升压模式下不同输入电压时的输入、输出电压，电感电流及S1（或S2）漏源极（drain-source）电压波形。在22.4V输入400V/500W输出时，低压输入侧电感电流峰值低于7A，不同输出电压下电感电流纹波均小于1A。另外，S1（S2）上的电压峰值约120V。图5d为CCM升压模式下各通道的电感电流波形，可以看出，当L1～L4电感量偏差在±5%以内且没有外加均流控制电路时，基于开关电容的自动均流系数大于0.95，实现了良好的均流效果。

图6为CCM降压模式下，输入400V，输出约24V时的实验波形。其中图6a为输入、输出电压，电感电流及Q3漏源极电压波形。可以看出，此时电感电流峰值约6.2A，纹波仍小于1A，考虑开关时刻的过渡过程，Q3上的电压峰值为210V。图6b显示了通道1～3的电感电流和Q3驱动信号波形，可见此时自动均流系数仍大于0.95。

图5 CCM升压模式下的实验波形Fig.5 Experimental waveforms under CCM Step-up mode

综上，所提出的变换器拓扑通过通道数量的增加，可显著降低各功率器件的电流应力。通过耦合电感的使用，可将通道内电流纹波降低至1A以下，达到普通双向Buck/Boost变换器的水平，同时，功率器件的电压应力仅为0.5VH。

如图7所示为DCM升压模式下的轻载实验波形，等效负载为3kΩ电阻。可以看出在近似空载时变换器处于电感电流临界连续状态，即电感电流近似临界连续，其负向谐振电流峰值小于0.08A。这得益于SiC功率MOSFET极低的输出等效电容（Coss=80pF）。

图6 CCM降压模式下的实验波形Fig.6 CCM Step-down mode experimental results

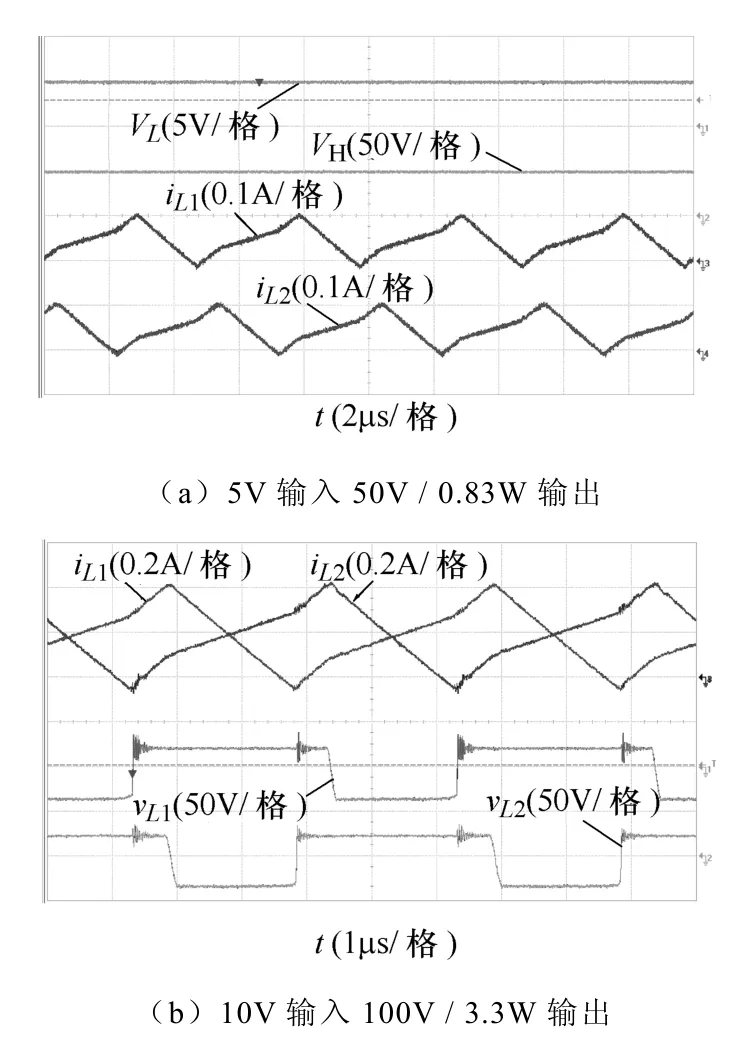
图7 升压模式下的轻载实验波形Fig.7 Step-up mode experimental results under lightly loaded conditions

图8为变换器效率曲线，分别给出了升压模式和降压模式时效率与输入功率的关系。在升压模式下，系统满载效率约96%，而降压模式下系统的满载效率则降低至94.8%。从图8中可以看出，升压模式下系统效率要明显高于降压模式下系统效率，这与文献[12]的理论分析相符，同时与诸多类似结构的双向变换器测试结果以及文献[13-15]相符。另外，由于轻载时电路可以实现开关管软开关的零电压开通，变换器在30%～120%负载范围内，系统效率波动较小。

图8 变换器效率Fig.8 Measured efficiency of the prototype

5 结论

本文提出了一种基于开关电容和耦合电感的交错并联型双向高电压增益DC-DC拓扑。该拓扑克服了传统非隔离型高电压增益双向变换器存在的诸多问题。根据500W样机实验结果，可以看出：通过并联通道数量的增加，该拓扑显著降低了各功率器件的电压和电流应力。同时，采用耦合系数优化设计后的耦合电感，进一步减小了电感量和电感体积，降低了通道内电感电流纹波，改善了变换器自动均流时的动态性能。不同工作模式下，电感电流纹波小于1A，自动均流系数高于0.95，各开关管的电压应力最大约为VH/2。变换器在升压和降压模式下可分别达到96%和94.8%的满载效率。证明了所提出的变换器拓扑非常适用于大功率储能充放电应用场合。

[1] Chen Zhangyong, Xu Jianping. High Boost ratio DC-DC converter with ripple-free input current[J]. Electronics Letters, 2014, 50(5): 353-355.

[2] 李武华, 何湘宁, 吴剑勇. 隔离型三绕组耦合电感交错式DC-DC变换器[J]. 电工技术学报, 2009, 24(9): 99-106. Li Wuhua, He Xiangning, Wu Jianyong. Isolated interleaved DC-DC converters with winding-cross coupled inductors[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 99-106.

[3] 罗全明, 闫欢, 孙明坤, 等. 基于拓扑组合的高增益Boost变换器[J]. 电工技术学报, 2012, 27(6): 96-102. Luo Quanming, Yan Huan, Sun Mingkun, et al. High step-up Boost converter based on topology combination[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 96-102.

[4] Zhu G, Ioinovici A. DC-to-DC converter with no magnetic elements and enhanced regulation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(2): 499-506.

[5] 涂文娟, 丘东元, 张波. DC/DC 谐振开关电容变换器潜电路发生的一般规律分析[J]. 电工技术学报, 2007, 22(12): 98-103. Tu Wenjuan, Qiu Dongyuan, Zhang Bo. General law of sneak circuit analysis in resonant switched capacitor DC/DC converters[J]. Transactions of China Electrotechnical Society, 2007, 22(12): 98-103.

[6] 夏守行, 张佐理. 一种谐振开关电容变换器的再分析与改进[J]. 电工技术学报, 2013, 28(4): 126-132. Xia Shouxing, Zhang Zuoli. Analysis and improvement of a resonant switched capacitor converter[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 126-132.

[7] Jung J H, Kim H S, Ryu M H. Design methodology of bidirectional CLLC resonant converter for highfrequency isolation of DC distribution systems[J]. IEEE Transactions on Power Electronics, 2012, 28(4), 1741-1755.

[8] Law K K, Cheng K W E, Yeung Y P B. Design and analysis of switched-capacitor-based step-up resonant converters[J]. IEEE Transactions on Circuits and Systems, 2005, 52(5): 943-948.

[9] Lee Y S, Chiu Y Y. Zero-current-switching switchedcapacitor bidirectional DC-DC converter[J] IEE Proceedings-Electric Power Applications, 2005, 152(6): 1525-1530.

[10] 陆治国, 郑路遥, 马召鼎, 等. 带开关电容网络的交错并联高增益Boost变换器[J]. 电工技术学报, 2012, 27(11): 153-159. Lu Zhiguo, Zheng Luyao, Ma Zhaoding, et al. Interleaved high gain Boost converter with switched capacitor network[J]. Transactions of ChinaElectrotechnical Society, 2012, 27(11): 153-159.

[11] 陆治国, 祝万平, 刘捷丰, 等. 一种新型交错并联双向DC/DC变换器[J]. 中国电机工程学报, 2013, 33(12): 39-46. Lu Zhiguo, Zhu Wanping, Liu Jiefeng, et al. A novel interleaved parallel bidirectional DC/DC converter[J] Proceedings of the CSEE, 2013, 33(12): 39-46.

[12] Slobodan M, Ćuk. Modelling, analysis, and design of switching converters[D]. Pokfulcom, Hong Kong: California Institute of Technology, 1976.

[13] Duan R Y, Lee J D. High-efficiency bidirectional DC-DC converter with coupled inductor[J]. IET Power Electronics, 2012, 5(1): 115-123.

[14] Lee Y S, Chiu Y Y. Zero-current-switching switchedcapacitor bidirectional DC-DC converter[J]. Proceedings-Electric Power Applications, 2005, 152(6): 1525-1530.

[15] Ardi H, Ahrabi R R, Ravadanegh S N. Non-isolated bidirectional DC-DC converter analysis and implementation[J]. IET Power Electronics, 2014, 7(12): 3033-3044.

Interleaved High Gain Bidirectional DC-DC Converter with Switched Capacitor and Coupled Inductor

Xue Likun1Wang Ping1Wang Yifeng1Yan Haiyun1Zhang Qiliang2
（1. Key Laboratory of Smart Grid of Ministry of Education Tianjin University Tianjin 300072 China 2. State Grid Jining Power Supply Company Jining 272200 China）

This paper proposes a high voltage ratio interleaved bidirectional DC-DC converter with switched capacitor and coupled inductor. The number of parallel channels is increased to realize higher voltage gain, greater output power, and lower device voltage/current stress. The coupled inductors can reduce current ripples and minimize the inductance in each channel, further increase the power density and efficiency of the converter. Additionally, low inductance accelerates the dynamic process of automatic current sharing by switched capacitors. A simple control strategy is adopted to facilitate circuit applications. Experimental verification of the proposed topology is performed using a 500-W prototype converter built in the laboratory.

Bidirectional DC-DC converter, energy storage, switched capacitor, coupled inductor, interleaved, high voltage gain

TM46

薛利坤 女，1988年生，硕士研究生，研究方向为高频电力电子变换技术。

E-mail: xuelikun@tju.edu.cn（通信作者）

王 萍 女，1959年生，博士，教授，博士生导师，研究方向为电力电子变换技术及其控制、智能检测与控制、电子电路与系统。

E-mail: pingw@tju.edu.cn

国家自然科学基金项目（51307117、51207104）和天津市科技支撑计划重点项目（14ZCZDGX00035）资助。

2014-10-05 改稿日期 2015-10-21