基于小波近似熵的串联电弧故障识别方法

郭凤仪 李 坤 陈昌垦 刘艳丽 王喜利 王智勇

（辽宁工程技术大学电气与控制工程学院 葫芦岛 125105）

基于小波近似熵的串联电弧故障识别方法

郭凤仪 李 坤 陈昌垦 刘艳丽 王喜利 王智勇

（辽宁工程技术大学电气与控制工程学院 葫芦岛 125105）

根据UL1699标准搭建了串联电弧故障发生装置，并针对不同类型负载进行实验，获得了供电线路正常工作状态和发生电弧故障状态时的电流信号实验数据。应用小波变换对电流信号进行分解重构，通过近似熵（ApEn）算法对分解重构后各频段信号的不规则程度进行量化，得到电流信号的特征向量，并将其输入到支持向量机（SVM）。通过SVM对电流信号特征向量进行分类，完成电弧故障的检测识别。结果表明，通过小波近似熵算法得到的电弧故障特征向量能够作为诊断识别电弧故障的有效依据。

电弧故障 近似熵 特征向量 小波分解 支持向量机

0 引言

近年来人们的防火意识显著提高，电气火灾逐渐引起人们的关注。2010年全国共接报火灾13.17万起，由电气原因引起的火灾40 481起，占30.7%，在69起较大火灾中，有24起为电气原因引起，占34.8%。在电力线路中，虚连、电缆材料绝缘老化、接线不规范、器件质量不合格等都会引发串联电弧故障，由于其电流在断路器额定电流2～5倍范围内，所以不会被短路、过电流等保护器件检测到，这就造成串联电弧故障在不为人知的情况下进一步加剧，最终造成火灾。由此可见，有效地识别电弧故障是保证安全供电、预防电气火灾的关键。

Muller利用傅里叶变换对串、并联电弧故障的频域特性进行研究，发现电弧故障发生时电路中会产生大量高次谐波[1]。Brechtken研究表明，随着电流和功率因数的增加，发生故障电弧时电流信号中掺杂的3次、5次和7次谐波幅值减小[2]。Zeller对电弧故障进行了建模和仿真研究[3,4]。国内根据电弧故障发生时电路中谐波量的变化提出了多种电弧故障检测方法[5-9]，其中较为典型的是利用小波变换理论从能量角度判断是否发生电弧故障[5]。

本文利用近似熵理论对发生电弧故障时电流信号变化的不规则程度进行量化，构建出近似熵特征向量，并将其输入到支持向量机（Support Vector Machine, SVM）分类器进行分类，实现串联电弧故障的诊断识别。

1 实验装置及实验结果

1.1 实验装置

为便于开展电弧故障实验，参照UL1699标准搭建了一套串联电弧故障实验装置[10]，如图1所示。实验线路如图2所示，将电弧故障实验装置的两个电极分别与电源和负载串联构成主回路，采用电流和电压互感器同时采集线路有无电弧故障时的回路电流信号和电极两端的电压信号，用于提取电弧故障特征，进而识别电弧故障。

图1 串联电弧故障实验装置Fig.1 Series arc fault experimental device

图2 实验原理Fig.2 Experimental principle

1.2 实验方案及结果

实验采用灯泡、电钻、计算机、角磨机、电磁炉和三相电机共六种负载，其中灯泡负载又分为4×200W、8×200W和12×200W三组不同工作状态。具体实验条件见表1。

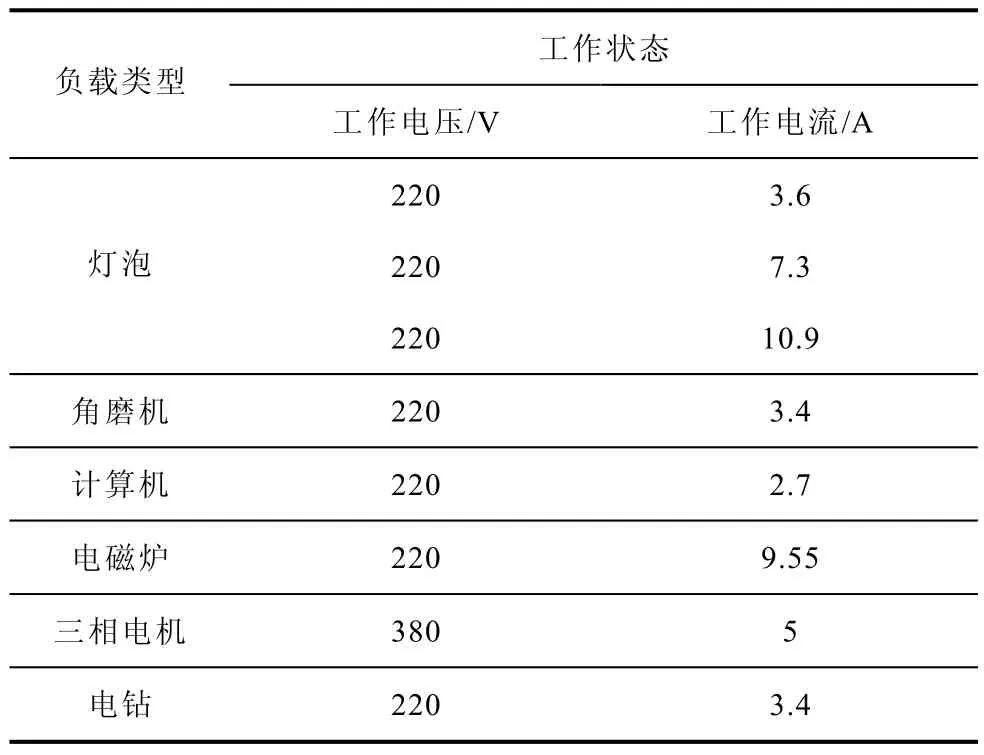
表1 实验条件Tab.1 Experimental conditions

图3为灯泡负载在线路正常状态和电弧故障状态时的电流波形，对比发现电弧故障时可以观察到很明显的平肩部，即“零休”。图4～图8分别计算机、角磨机、电磁炉和三相电机负载在线路正常状态和电弧故障状态时的电流波形，发现电弧故障时电流信号产生了明显的畸变。

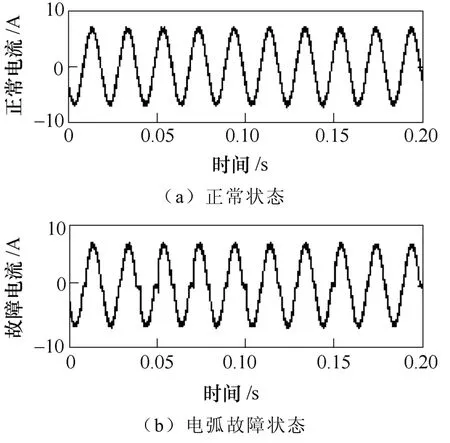
图3 灯泡负载实验波形对比Fig.3 Current waveforms for lamb load

图5 角磨机负载实验波形对比Fig.5 Current waveforms for angle grinder load

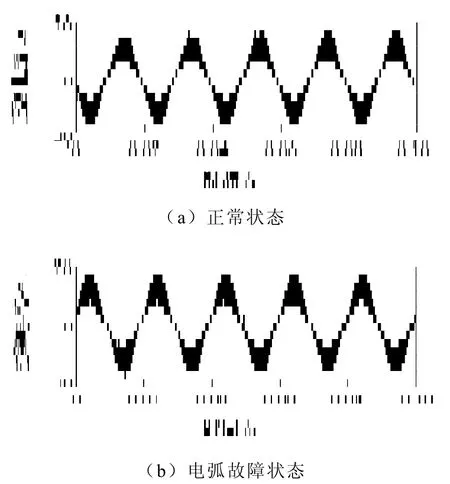
图6 电磁炉负载实验波形对比Fig.6 Current waveforms for electromagnetic oven load

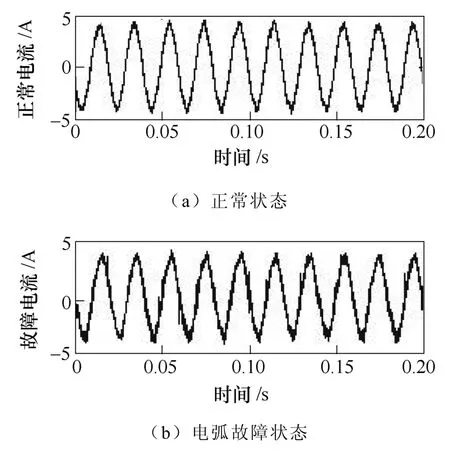
图7 三相电机负载实验波形对比Fig.7 Current waveforms for three-phase motor load

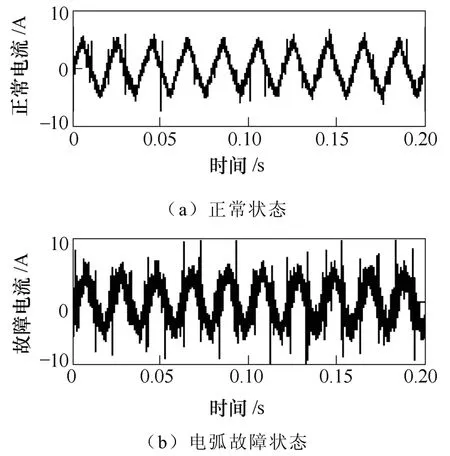
图8 电钻负载实验波形对比Fig.8 Current waveforms for electric drill load

2 特征向量的提取

发生电弧故障时电流信号会发生奇异性变化，其原因是电流信号中掺杂了大量的谐波信号[1]。本文首先利用小波变换对电流信号进行分解、重构以得到细节信号，再利用近似熵理论对电流信号变化的不规则程度进行量化，通过提取各层电流细节信号的近似熵组成电弧故障的特征向量并作为SVM的输入。图9为特征向量提取过程示意图。

图9 特征向量提取过程示意图Fig.9 Feature vector extraction process

2.1 信号阈值降噪

电路中的其他噪声信号会干扰故障电弧特征量的提取，因此在提取特征量之前需要对电流信号进行降噪处理。通过比较多种降噪处理方法，本文利用Matlab软件中的ddencmp函数获取电流信号的降噪阈值利用wdencmp函数选用db4小波包对电流信号进行6层分解和阈值降噪。图5为8×200W灯泡负载降噪前后的电流信号。

图10表明，经阈值降噪以后，电流波形中的“毛刺”明显减少，电弧故障产生的“平肩部”特征依然保留完好，达到了去除干扰噪声、保留电弧故障特征信息的目的。

2.2 小波变换

发生电弧故障时电路电流会发生不同程度的畸变，这种畸变是不稳定的，并且会随着电压、空气湿度、绝缘介质导电性等条件而变化，因此单纯利用电流信号的变化来判定是否发生电弧故障是片面的。近年来已有多种信息处理方法检测电弧故障，其中最典型的是傅里叶变换和小波分析。傅里叶变换将时域信号转换到频域中进行分析，但是却完全忽视了信号的时域特征。小波变换将信号分解为多频段信号，各频段信号中同时含有信号的时域特征和频域特征[11-14]，并且信号的不规则程度会在时域和频域均有所体现。因此，小波变换更适合对信号的不规则程度进行描述。

图10 阈值降噪前后电流波形Fig.10 Current waveforms before and after threshold denoising for lamb load

本文利用db5小波将电流信号分解为多层信号，利用从多层信号中提取出的多层判据来诊断电弧故障。图11为四层小波变换示意图。在获得的各层信号中，A为低频分量，D为高频分量。高频分量包含着原始信号中的随机和干扰信息，低频分量更多地包含着原始信号的主要趋势。A4、D1、D2、D3和D4既包含电流信号的主要趋势，又包含电流信号中干扰噪声信号的信息，因此，选用A4、D1、D2、D3和D4来进行特征值提取。

8×200W灯泡负载在线路正常状态和电弧故障状态时电流信号的小波分解重构信号分别如图12、图13所示。

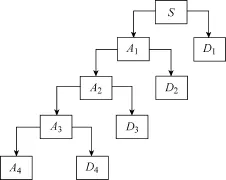
图11 四层小波变换示意图Fig.11 Diagram of four layer wavelet transform

图12 灯泡负载正常状态下小波细节信号Fig.12 Wavelet details under normal conditions

图13 灯泡负载故障状态下小波变换细节信号Fig.13 Wavelet details under arc fault conditions

由图12、图13可见，电弧故障时电流信号掺杂较明显的高频成分，经小波变换后的各频段信号的不规则程度发生了变化。

2.3 近似熵

由Pincus提出的近似熵能够描述时间序列复杂程度，目前已被应用于医学、机械设备状态监测和故障诊断等领域[15-19]。由于电弧故障会使电流信号经小波变换后的各层频段信号产生不同程度的变化，这种变化可以直接反映为信号不规则程度的变化，因此可以用近似熵来组建电弧故障的特征向量。

计算时间序列信号S，S={u1,u2,…,un}（S由n个等间距数据点所组成）的近似熵，过程如下。

（1）确定维数m，用时间序列信号S构造一组m维向量

（2）将以上构造向量中任意两向量之间的距离

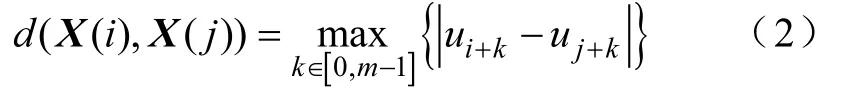
（3）计算以上构造向量中任意两向量之间的关联程度

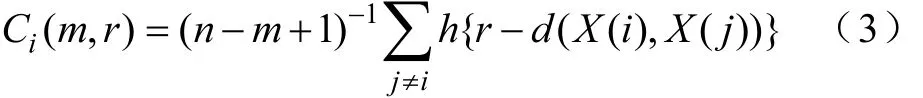
式中，h(⋅)为Heaciside函数；r为相似容限。

（4）计算矢量序列{X(n)}的平均自相关程度

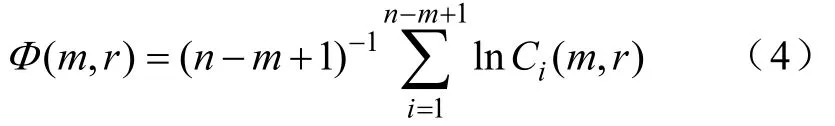
（5）求解近似熵Sa

求解近似熵求解需要确定三个待定参数m、n和r。Pincus针对这三个参数作了具体分析，当时间序列采样点n=1000，维数m=2，相似容限r=0.1～0.2STD(STD为序列的标准差)时，近似熵的值统计趋于稳定。因此取n=1000，m=2，r=0.15STD。图14为近似熵计算流程。

图14 近似熵计算流程Fig.14 Flow chart of approximate entropy calculation

2.4 特征向量比较

电流信号经过阈值降噪、小波分解和近似熵计算以后，便得到了电流信号在D1、D2、D3、D4和A4各频段细节信号的近似熵，利用这些近似熵构造电弧故障的特征向量。表2～表5即为各种负载下电弧故障信号的特征向量。

表2 灯泡负载特征向量Tab.2 Feature vector for lamb load

表3 计算机和电磁炉负载特征向量Tab.3 Feature vector for computer and electromagnetic oven load

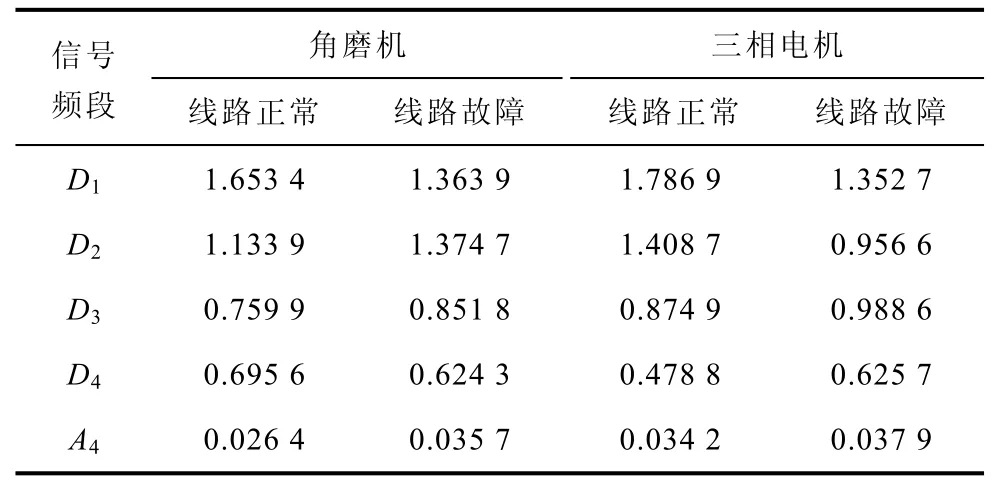
表4 角磨机和三相电机负载特征向量Tab.4 Feature vector for angle grinder and three phase motor load

表5 灯泡和电钻负载特征向量Tab.5 Feature vector for lamb and electric drill load

3 串联电弧故障的诊断

3.1 诊断算法

SVM不仅具有很好的通用性、鲁棒性及有效性，而且计算简单、速度快[20]，适用于串联电弧故障的快速诊断。SVM做分类预测时需要选择核函数并且选择合适的参数（惩罚参数c和核函数参数g）以便获得比较理想的预测效果。本文选用径向基函数作为SVM核函数（见式（6）），应用经粒子群优化（Particle Swarm Optimization, PSO）算法优化惩罚参数c和核函数参数g。图15为PSO优化SVM参数的算法流程，其中CV指交叉验证方式。

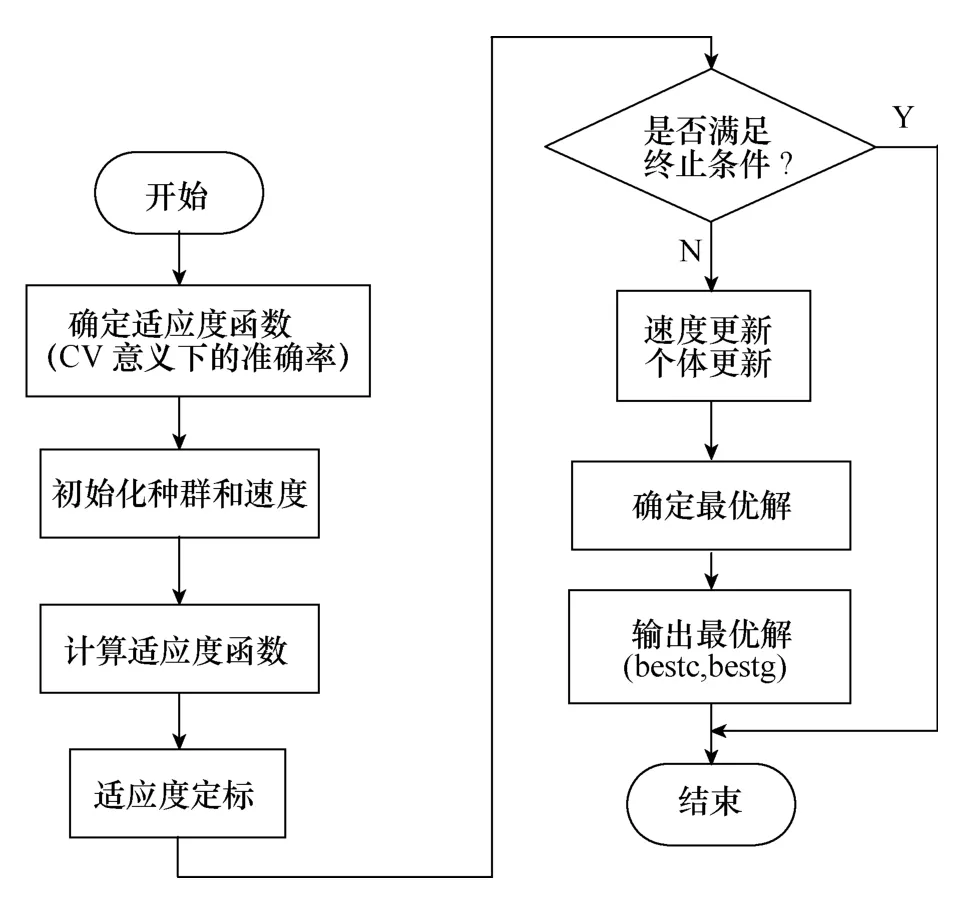
图15 PSO优化SVM算法流程Fig.15 Flow chart of PSO optimization algorithm

径向基核函数

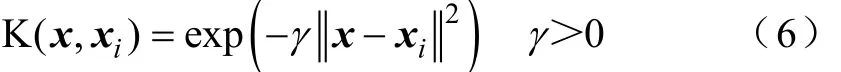
将4×200W灯泡、8×200W灯泡、计算机、角磨机、电磁炉和三相电机作为已知负载，将12×200W灯泡和电钻作为未知负载。用已知负载电流信号特征向量对SVM进行训练，用已知负载和未知负载电流信号特征向量共同测试训练后的SVM的诊断能力。

3.2 已知负载的诊断结果分析

首先，将已知负载在线路正常和电弧故障状态下的电流信号特征向量各取50%作为训练数据，预定训练准确率为100%。然后，将剩下的50%作为测试数据进行测试诊断。在此过程中，类别标签分配见表6。

表6 类别标签分配Tab.6 The class label distribution

SVM识别结果见表7。由表7可见，计算机、角磨机、电磁炉和三相电机共四种负载的电流信号特征向量经过SVM后识别率较高，最高达到97.5%，达到了有效识别电弧故障的目的。灯泡负载电弧故障诊断识别率较低，低于60%，还需要进一步分析。因此，针对灯泡负载经SVM分类后的识别标签进行了统计，如图16、图17所示。

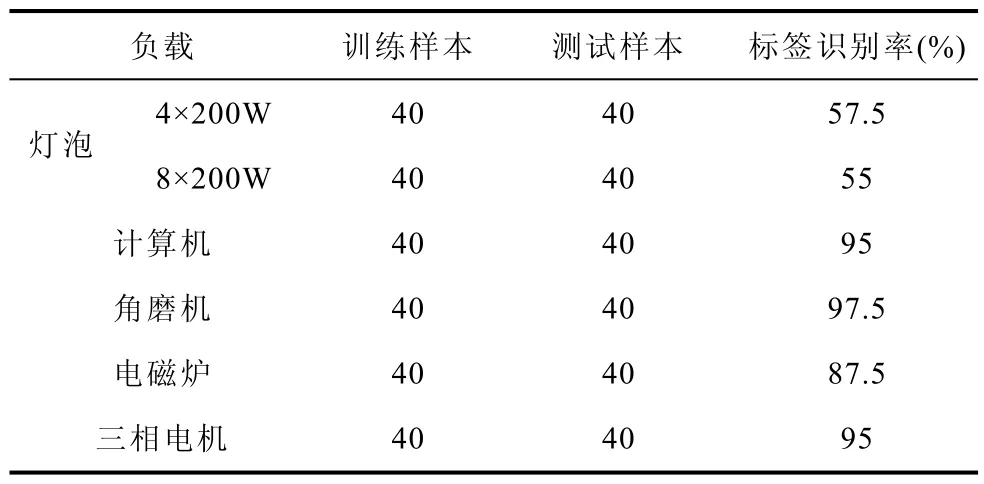
表7 SVM识别结果Tab.7 The fault recognition results of SVM

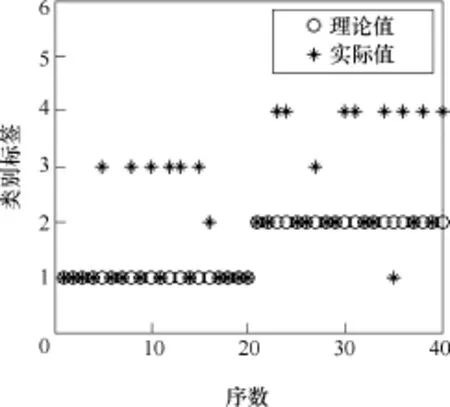
图16 4×200W灯泡负载识别标签统计Fig.16 Identification tag statistics for 4×200W lamb load

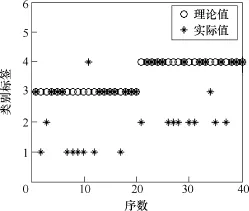
图17 8×200W灯泡负载识别标签统计Fig.17 Identification tag statistics for 8×200W lamb load

由图16、图17可知，在识别过程中，4×200W灯泡与8×200W灯泡两组负载在线路正常时的电流信号特征向量产生了相互影响，在电弧故障时电流信号特征向量也产生了相互影响，而同一组灯泡在不同状态下的电流信号特征向量相互影响很小，识别标签均在两组识别标签范围内（1～4）。针对这种情况，将两组灯泡负载合并成为一组负载，合并后用类别标签“2”和“3”分别代表灯泡负载在线路正常状态和电弧故障状态，重新对SVM进行训练和测试，诊断结果见表8。

表8 SVM已知负载识别结果Tab.8 The SVM recognition results for known load

将4×200W和8×200W灯泡负载合并为一组负载后，识别率提高到了97.5%，并且对其他负载条件下的识别结果没有产生明显影响。

3.3 未知负载的诊断结果分析

分别将12×200W灯泡负载和电钻负载的电流信号近似熵特征向量输入到已经训练好的SVM进行故障识别。

表9为未知负载通过构造近似熵特征向量后SVM的识别结果。12×200W灯泡负载的识别率达到了98%，识别标签为2和3，落在了灯泡负载的识别标签范围内；电钻负载的识别率达92%，识别标签为7和8，落在了角磨机负载的识别标签范围内。

表9 SVM未知负载识别结果Tab.9 The SVM recognition results for unknown load

4 结论

本文研制了串联电弧故障实验装置，根据串联电弧故障时电流信号的不规则程度会发生变化的特点，提取出电流信号经小波变换后各层频段信号的近似熵值，构造特征向量作为支持向量机的输入，对串联电弧故障进行了识别。由负载标签识别率统计结果可知，在已知负载中，灯泡做负载时识别率最高，达到97.5%，角磨机做负载时识别率最低，达到85%，实现了已知负载条件下电弧故障的有效识别；未知负载的识别率高于92%，识别系统具有可延拓性。

结果表明，将小波近似熵特征向量作为检测识别串联电弧故障的特征值输入到支持向量机，识别率较高，能够有效地识别串联电弧故障。

[1] Muller P, Tenbohlen S. Characteristics of series and parallel low current arc faults in the time and frequency domain[C]//The 56th IEEE Holm Conference on Electrical Contacts, Charleston, SC, 2010: 1-7.

[2] Brechtken D. Precentive arc fault protection[C]// IEEE/PES Transmission and Distribution Conference, USA, 2001, 1: 311-316.

[3] Zeller P. A simple arc model for the simulation of the clearing time of drawn arcs with a commercial electronics simulation tool[C]//The 55th IEEE Holm Conference on Electrical Contacts, Vancouver, British Columbia, Canada, 2009: 67-74.

[4] Andrea J, Schweitzer P, Tisserand E. A new DC and AC arc fault electrical model[C]//The 56th IEEE Holm Conference on Electrical Contacts, Charleston, SC, 2010: 210-215.

[5] 张士文, 张峰, 王子骏, 等. 一种基于小波变换能量与神经网络结合的串联型故障电弧辨识方法[J].电工技术学报, 2014, 29(6): 290-302. Zhang Shiwen, Zhang Feng, Wang Zijun, et al. Series arc fault identification method based on energyproduced by wavelet transformation and neural network[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 290-302.

[6] 雍静, 桂小智, 牛亮亮, 等. 基于自回归参数模型的低压系统串联电弧故障识别[J]. 电工技术学报, 2011, 26(8): 213-219. Yong Jing, Gui Xiaozhi, Niu Liangliang, et al. Series arc fault identification in low voltage system based on autoregressive parameter model[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 213-219.

[7] 刘晓明, 赵洋, 曹云东, 等. 基于小波变换的交流系统串联电弧故障诊断[J].电工技术学报, 2014, 29(1): 10-17. Liu Xiaoming, Zhao Yang, Cao Yundong, et al. Series arc fault diagnosis based on wavelet transform in AC system[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 10-17.

[8] 孙鹏, 董荣刚, 郑志成. 基于小波分析信号特征频段能量变比的故障电弧诊断技术研究[J]. 高压电器, 2010, 46(7): 46-50. Sun Peng, Dong Ronggang, Zheng Zhicheng. Arc fault diagnosis technology based on the analysis of energy variation of signal’s characteristic frequency band with wavelet transform[J]. High Voltage Apparatus, 2010, 46(7): 46-50.

[9] 刘艳丽, 郭凤仪, 王智勇, 等. 基于信息熵的串联型故障电弧频谱特征研究[J]. 电工技术学报, 2015, 30(12): 488-495. Liu Yanli, Guo Fengyi, Wang Zhiyong, et al. Research on the spectral characteristics of seriesarc fault based on information entropy[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 488-495.

[10] UL standard for safety for arc fault circuit interrupters[S]. 2ed. ANSI UL1699, 2008.

[11] 张鹏, 李红斌. 一种基于离散小波变换的谐波分析方法[J]. 电工技术学报, 2012, 27(3): 252-259. Zhang Peng, Li Hongbin. A novel algorithm for harmonic analysis based on discrete wavelet transforms[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 252-259.

[12] 张冠英，张晓亮，刘华，等. 小低压系统串联故障电弧在线检测方法[J]. 电工技术学报, 2016, 31(8): 109-115. Zhang Guanying, Zhang Xiaoliang, Liu Hua, et al. Online detection method for series arcing fault in low voltage system[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 109-115.

[13] 行晋源, 李庆民, 丛浩熹, 等. 长距离输电线路潜供电弧弧根跳跃与弧长剧变的物理机制与仿真[J].电工技术学报, 2016, 31(12): 90-98. Xing Jinyuan, Li Qingmin, Cong Haoxi, et al. Physical mechanism and simulation method of the arc root jumping and arc length variation of the secondary arcs with long-distance[J]. Transmission Lines Transactions of China Electrotechnical Society, 2016, 31(12): 90-98.

[14] 王智勇, 郭凤仪, 王海潮, 等. 矿用栓接电缆接头松动故障识别方法研究[J]. 煤炭学报, 2016, 41(4): 1045-1051. Wang Zhiyong, Guo Fengyi, Wang Haichao, et al. Research on identification methods of looseness fault in coal-mine bolted cable joint[J]. Journal of China Coal Society, 2016, 41(4): 1045-1051.

[15] 符玲, 何正友, 麦瑞坤, 等. 近似熵算法在电力系统故障信号分析中的应用[J]. 中国电机工程学报, 2008, 28(28): 68-73. Fu Ling, He Zhengyou, Mai Ruikun, et al. Application of approximate entropy to fault signal analysis in electric power system[J]. Proceedings of the CSEE, 2008, 28(28): 68-73.

[16] 栗然, 陆凤怡, 徐宏锐, 等. 基于局域波与近似熵的负荷分析方法[J].中国电机工程学报, 2010, 30(25): 51-58. Li Ran, Lu Fengyi, Xu Hongrui, et al. Novel approach for load analysis based on local wave and approximate entropy[J]. Proceedings of the CSEE, 2010, 30(25): 51-58.

[17] 殷家敏，吉畅，罗建. 基于电容序列近似熵的消弧线圈接地选线方法[J]. 电力系统保护与控制, 2015, 43(17): 45-50. Yin Jiamin, Ji Chang, Luo Jian. Fault line selection approach of extinction coil based on capacitance sequence approximate entropy[J]. Power System Protection and Control, 2015, 43(17): 45-50.

[18] 郭磊, 王瑶, 于洪丽, 等. 基于近似熵的磁刺激穴位脑功能网络构建与分析[J]. 电工技术学报, 2015, 30(10): 31-38.Guo Lei,Wang Yao, Yu Hongli, et al. Brain network based on approximate entropy of EEG under magnetic stimulation at acupuncture point[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 31-38.

[19] 林丽, 赵德有. 基于局域波近似熵的声发射信号处理[J]. 大连理工大学学报, 2010, 50(1): 75-80. Lin Li, Zhao Deyou. Acoustic emission signal processing based on local wave and approximate entropy[J]. Journal of Dalian University of Technology, 2010, 50(1): 75-80.

[20] 薛浩然，张珂珩, 李斌, 等. 基于布谷鸟算法和支持向量机的变压器故障诊断[J]. 电力系统保护与控制，2015, 43(8): 8-13. Xue Haoran, Zhang Keheng, Li Bin, et al. Fault diagnosis of transformer based on the cuckoo search and support vector machine[J]. Power System Protection and Control, 2015, 43(8): 8-13.

Series Arc Fault Identification Method Based on Wavelet Approximate Entropy

Guo Fengyi Li Kun Chen Changken Liu Yanli Wang Xili Wang Zhiyong
（Faculty of Electrical and Control Engineering Liaoning Technical University Huludao 125105 China）

A series arc fault generator was built according to UL1699. Experiments were carried out under different load conditions. Loop current waveforms with and without series arc fault were obtained. Firstly, the current signal was decomposed and reconstructed by wavelet transform. Then the irregular degrees of signals in each frequency band were quantified with approximate entropy algorithm, and the feature vectors of current signals were obtained. Finally, all the feature vectors were used as input variables of support vector machine (SVM). The series arc fault can be recognized by classifying those feature vectors with SVM. It is shown that the feature vectors obtained by wavelet approximate entropy algorithm can diagnose series arc fault.

Arc fault, approximate entropy, feature vector, wavelet decomposition, support vector machine

TM501

郭凤仪 男，1964年生，教授，博士生导师，研究方向为电器基础理论与应用。

E-mail: fyguo64@126.com（通信作者）

李 坤 男，1987年生，硕士研究生，研究方向为电器基础理论与应用。

E-mail: lflikun318@163.com

国家自然科学基金资助项目（51277090、51674136）。

2014-10-24 改稿日期 2014-12-19