基于分数阶联合卡尔曼滤波的磷酸铁锂电池简化阻抗谱模型参数在线估计

李晓宇 朱春波 魏 国 逯仁贵

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

基于分数阶联合卡尔曼滤波的磷酸铁锂电池简化阻抗谱模型参数在线估计

李晓宇 朱春波 魏 国 逯仁贵

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

电池特性建模及模型参数在线估计是电动汽车电池管理系统的关键技术，以磷酸铁锂电池这一非线性系统为研究对象，以包含分数阶元件的简化电池电化学阻抗谱模型为基础，建立了该模型的状态转移方程和系统观测方程，运用分数阶联合卡尔曼滤波器（FJKF）对该模型的扩散极化电压和模型参数进行了在线估计。试验结果表明，该模型能较好地表征磷酸铁锂电池的动态特性，分数阶联合卡尔曼滤波算法在参数估计过程中能够保持很好的精度，同时该方法对多种测试工况都有较好的适用性，算法估计得到的模型参数值具有较好的稳定性。

磷酸铁锂电池 分数阶电池模型 电化学阻抗谱 分数阶联合卡尔曼滤波

0 引言

随着汽车技术的发展，代表新一代节能与环保汽车发展方向的电动汽车开始逐渐被推广应用[1]，磷酸铁锂电池因其高安全性而日益广泛地应用于电动汽车。动力电池作为电动汽车的能量存储与供给单元，对其进行有效的监测和管理是电动汽车安全、高效运行的基本保障[2]。目前，动力电池的状态监测和管理技术主要有电池荷电状态（State Of Charge, SOC）估计技术[3,4]、峰值功率预测技术[5]（State OfPower, SOP）、电池健康状态（State Of Health，SOH）估计、寿命预测技术[6]（Remain Useful Life, RUL）、电池老化机理无损分析技术[7]、冷热管理技术等，为了更好地实现对储能系统的监测与管理，依据适当的电池模型[8,9]、电池端电压和负载电流等数据求解电池模型的状态、参数[10]以及变化情况，进而实现系统的优化配置[11]管理。

常见的电池模型有等效电路模型、电化学反应机理模型及多物理场模型[12]等，等效电路模型形式简单、计算量小，并且能够有效地反映电池动态特性，在电池状态监测和管理领域有着广泛的应用。典型的等效电路模型有Rint模型、一阶RC模型、PNGV模型、二阶RC模型及电化学阻抗谱模型等。不同类型动力电池的外特性不尽相同，选用的等效电路模型也多种多样。其中，一阶RC模型计算量小、能够较好地反映多种电池的动态特性而被广泛地使用；电化学阻抗谱模型可以更好地反映多种动力电池的动态特性[13]，并且对比一阶RC模型，电化学阻抗谱模型中元件的物理意义更加明确，因而该电池模型越来越受到人们的关注。

C. Fleishcher等基于电化学阻抗谱技术建立电池等效电路模型，实现了电池的SOC估计[14]、SOH估计[15,16]以及SOP预测[17]，但是电化学阻抗谱模型也存在计算量大、模型参数难以在线估计等缺点，这在一定程度上制约了电化学阻抗谱模型在电池的状态监测和管理技术中的应用。

本文依据磷酸铁锂电池的电化学阻抗谱测试结果建立了一种等效电路模型，构建了算法所需的状态方程与观测方程，利用分数阶联合卡尔曼滤波器[18]（Fractional Joint Kalman Filter，FJKF），将电池模型中的准开路电压OCVe、欧姆内阻Ro、扩散极化参数XW和扩散极化电压UW作为估计量，将测得的电池端电压UL、负载电流IL以及采样的时间间隔Ts（Ts=1s）作为已知量。通过FJKF算法的迭代更新，实时地估计出所测磷酸铁锂电池的准开路电压、欧姆内阻及扩散极化参数。与传统的阻抗谱测试方法、一阶RC模型及卡尔曼滤波方法相比，本文提出的方法通过迭代求解，无需专用的电化学阻抗谱测试设备，即可在线估计出磷酸铁锂电池的电化学阻抗谱分布情况。电池模型的仿真精度优于一阶RC模型，模型参数值的稳定性优于传统的电池参数在线估计算法，该方法可以为动力电池的状态监测和管理提供可靠的依据。

1 等效电路模型的建立

1.1 动力电池使用工况分析

动力电池使用工况的特征在一定程度上决定了电池模型应有的精细化程度。汽车常见的运行工况大致可以分为两种：市区工况和城郊工况，对应的典型测试工况有美国《USABC电池测试手册》中的联邦城市（FUDS）工况、FTP75市区（FTP75 Urban）工况、FTP75市郊（FTP75 Suburb）工况等。图1对FTP75市区和市郊工况的车速、仿真得到的负载电流及其频率特性做了对比。主要仿真参数有：整车质量1 200kg，迎风面积1.97m2以及电池组参数336V/40A·h。

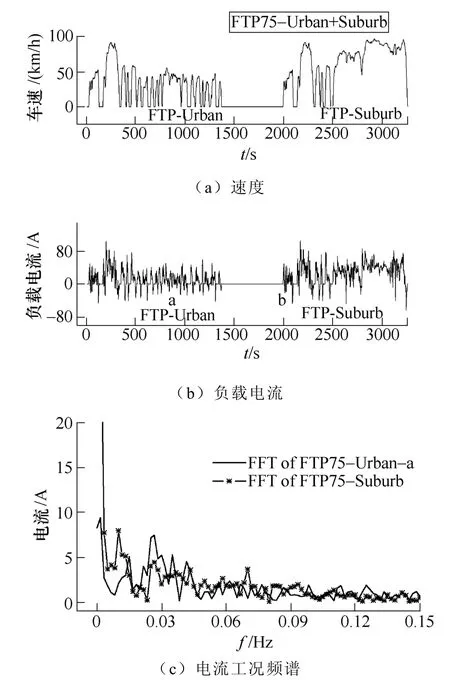
图1 FTP75 市区工况和市郊工况对比Fig.1 Comparison of the FTP75 urban and suburban vehicle working conditions

图1c频谱中，两种工况的频率成分均集中在很低的频率处，而存在的差异表现在FTP75-Urban-a（FTP75市区工况的稳态行车工况部分）的主要频谱成分比FTP-Suburb分散，FTP-Suburb工况频谱的最高和次高幅值均出现在基频附近。

因此，在电池建模时，表征电池中高频特性的电路元件可以被简化。由于不同运行工况的低频频率成分分布存在差异，因此用于表征电池低频特性

的电路元件应尽可能准确。

1.2 磷酸铁锂电池等效电路分析

建立电池等效电路的主要目的是使用电路元件表征电池电参数的动态变化，获取电池状态信息。图2描绘了磷酸铁锂电池的三种等效电路阻抗特性，其中“R-RQ-ZW”（Q为恒相位元件，ZW为韦伯阻抗元件）表示电化学阻抗谱模型，能够准确反映电池的阻抗谱，“R-RC”表示一阶RC模型，“R-2RC”表示二阶RC模型。对于本文研究的磷酸铁锂动力电池的电化学阻抗谱分布，图2中区域①对应的频谱范围约为1kHz～1Hz，区域②对应的频谱范围约为1Hz～0.05Hz，f表示频谱奈奎斯特图中测试频率。区域②右侧阻抗对应的测试频率逐渐减小，该阻抗成分通常被认为是电池扩散特性的外在反映。一阶RC模型的阻抗特性只在很小的频率范围内与电化学阻抗谱模型相似，二阶RC模型也同样没有明显改善。因此，使用低阶次的RC模型很难全面地表征电池的低频阻抗谱特性。然而，电化学阻抗谱模型中的ZW元件因其自身的特性可以较准确地表征电池的低频阻抗谱特性。

图2 电池等效电路模型对比Fig.2 Comparison of the battery equivalent circuit models

1.3 简化电化学阻抗谱模型的描述

通过上节的对比分析可以得出，在对磷酸铁锂电池建模时，电化学阻抗谱模型中的较高频率的阻抗特性（对应图2中①）可以由常用的RQ并联电路简化为纯阻性元件R，简化后得到的简化电化学阻抗谱等效电路模型如图3所示。

图3中，UL、IL分别为电池的端电压与流经电池的总电流，模型由OCVe、Ro、ZW三个元件构成。其中，OCVe为准开路电压元件，主要反映电池开路电压特性。

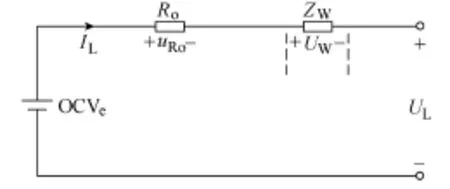
图3 简化的电化学阻抗谱模型Fig.3 A simplified electrochemical impedance spectroscopy model

由于电化学阻抗谱模型简化了电池化学反应动力学的许多过程，OCVe是电池开路电压（Open Circuit Voltage, OCV）的近似值，OCVe在数值上包含了OCV以及一部分由于扩散极化产生的过电动势。

式中，Ro为欧姆内阻特性元件，该参数主要反映电池电化学阻抗谱的中高频欧姆阻抗特性，参数在数值上约等于高频欧姆阻抗RΩ、固液界面（Solid Electrolyte Interface, SEI）膜阻抗RSEI、电荷转移阻抗Rct之和。

从电池的电化学阻抗谱测试数据可知，电池离子扩散特性可近似由0.5阶韦伯阻抗来描述[14]。韦伯阻抗定义式为

式中，W为离子扩散系数；ω为角频率。为了便于阻抗参数的在线估计，本文中取，得到

该等效电路模型的特点是简化了传统阻抗谱等效电路模型中的高频（频率大于1kHz）和中频阻抗（频率大于0.5Hz，且小于1kHz）电路，上述简化阻抗谱模型可以有效减少模型参数数量，并且适合用于电池的状态监测和管理。

2 电池模型的参数估计

2.1 状态方程的建立

根据已建立的包含分数阶元件的电池等效电路模型，将构建模型对应的状态方程与观测方程。

首先，取IL在放电时为正值，数据采样周期为Ts=1s，使用Δr作为微分算子，即

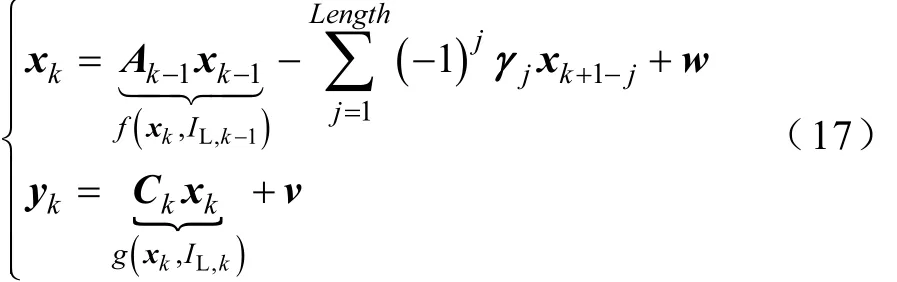
2.2 分数阶联合卡尔曼滤波参数估计

J. Sabatier和D. Sierociuk分别提出了两种分数阶元件参数的估计方法，一种是Levenberg-Marquart算法[19]，它是一种非线性最小二乘滤波算法，该算法的特点是根据函数梯度信息，不断寻找参数最优值的迭代过程。该方法的特点是需要计算待估参量的输出敏感度系数，然而对于分数阶元件，敏感度系数的计算十分复杂，且计算量大，不适合工程应用。另外一种方法是FJKF算法，该方法可以将分数阶元件参数作为隐性参量，在不计算参量的输出敏感度系数情况下即可获得参数的估计值。该算法的特点是分数阶元件参数的估计过程简单。另外，该算法有效利用了卡尔曼滤波算法的预测-修正的工作特点，使得参数估计过程的跟踪性能，参数估计精度都优于最小二乘滤波算法。但是该方法也有一定的局限性，当算法应用的模型结构复杂时，会造成滤波器发散。综合考虑上述两种方法的优缺点，由于本论文使用的简化电化学阻抗谱模型形式简单，模型状态和参数的估计方法选用FJKF算法。该算法的具体计算过程如下：

（1）初始化。取Qk为噪声wk的协方差，Rk为噪声vk的协方差，设定各个参量的初始值。

（2）状态、参数及协方差矩阵的时间更新。

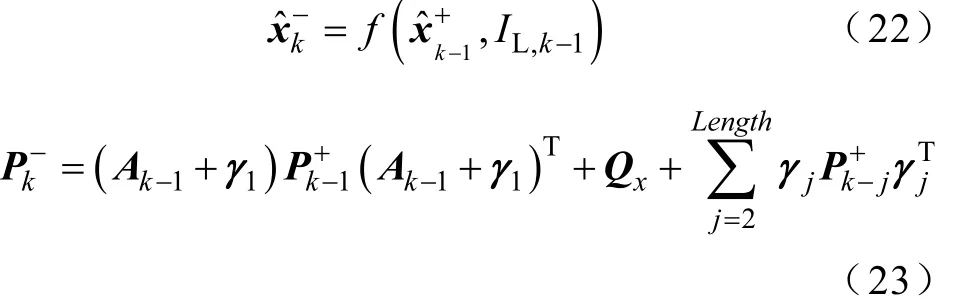
（3）状态、参数及协方差矩阵的测量更新。

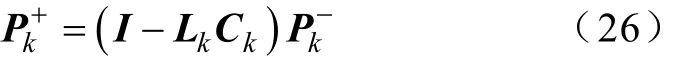
采用FJKF算法实现电池模型状态及参数的递推更新流程如图4所示。

图4 分数阶联合卡尔曼滤波算法流程Fig.4 Flow chart of the fractional joint Kalman filter

3 试验与数据分析

3.1 试验介绍

本文试验选用的电池是深圳沃特玛电池有限公司生产的额定容量为5A·h的LiFePO4/graphite 能量型动力电池，电池单体的上下限截止电压为3.65V和2.5V，每8个电池单体并联组成电池模块，然后105个电池模块串联可以组成额定电压为336V、额定电流为100A（2.5C）的动力电池包。本文的算法验证试验主要由Arbin BT2000电池测试系统完成，试验对象为磷酸铁锂电池单体，试验内容包括FUDS工况试验、FTP75市区和FTP75市郊混合工况试验，试验放电电流的最大值为12.5A（2.5C）。另外，实施了脉冲放电试验和电化学阻抗谱试验，用来获取电池开路电压的真值和电化学阻抗谱的真值，验证算法性能。试验环境为常温、常湿、标准大气压。

3.2 估计值与试验参考值对比

本文采用的FUDS测试工况最大放电功率为32W，在每个FUDS工况之间加入了5min的静置工况，两者循环执行，直至电池放电结束。通过此工况试验验证电池模型及参数估计值的准确性。图5a为数据采集系统得到的电池端电压UL和负载电流IL。图5b为FJKF算法计算得到的端电压的估计误差，可以看出，FJKF算法的端电压估计误差非常小，基本维持在5mV以内，而在工况测试的初期和末期误差较大，原因可能是模型参数在算法参数跟踪过程的初期误差较大所致，工况测试后期误差较大的原因可能是由电池模型误差引起的。

图5 FUDS工况数据及FJKF算法估计误差Fig.5 FUDS battery terminal voltage and load current data and FJKF estimation error

图6对采用FJKF算法计算得到的OCV估计值和采用脉冲放电静置1h得到的OCV参考值作了对比。从图6中看，OCV估计值基本与OCV参考值吻合，除了在电池电压从放电平台1向平台2过渡的区域，OCV估计值存在较大误差，此处的最大偏差值为20mV。

图6 OCV测试结果对比Fig.6 Comparison of open circuit voltage test result

图7对采用FJKF算法计算得到的阻抗谱估计值与传统电化学阻抗谱（Electrochemical Impedance Spectroscopy, EIS）测试方法得到的阻抗值进行对比。图7中，由于算法使用的电池模型对电池阻抗谱的中高频成分做了简化，因此，本文的阻抗谱估计值没有传统EIS方法测试得到的中高频信息（图7中区域1）。低频阻抗谱成分与传统EIS方法的结果基本吻合，但阻抗值略小。通过对电化学反应机理的分析，阻抗偏小的原因是电池在经历大电流充放电时，电池化学反应的动力学过程复杂，由于电极反应不均匀、Butler-Volmer等动力学过程会导致阻抗测试结果与传统EIS离线测试结果的偏离。但是该阻抗谱的估计值在数值上是对电池动力学过程的真实反应。

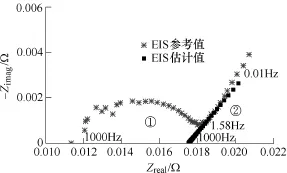
图7 电化学阻抗谱测试结果对比Fig.7 Comparison of EIS test results

3.3 参数估计值稳定性对比

图8对本文提出的方法与一阶RC电池等效电路模型和DEKF方法[20]的结果作了对比，FJKF的估计值（FJKF-OCVe）相对DEKF的估计值（DEKF-OCVe）更加稳定，DEKF-OCVe在数值上偏小于FJKF-OCVe，基于3.2节中的OCV的对比分析，FJKF-OCVe更接近OCV真值，因此DEKF-OCVe必然偏小于OCV真值。而DEKF-OCVe在电池处于静置的状态时，会出现升高并且逐渐接近OCV真值的现象，当再次对电池加载波动的电流激励之后，DEKF-OCVe则又逐渐地偏离OCV真值，该现象的原因是一阶RC模型不能准确地反映电池和工况的动态特性。

图8 算法模型参数估计值值稳定性对比Fig.8 Comparison of the model parameter stability

通过1.1节电动汽车运行工况分析可知，当工况存在波动的电流激励时，电流激励的频率成分非常丰富。（类似图1中FTP75-Urban-a的频谱分布情况），当电池处于静置工况后，电流激励的主要频率成分将逐渐向极低频区域移动，当工况电流恒定为零时，工况的主频率成分也接近为零。然而，一阶RC模型只能在一段频率范围内接近于阻抗谱的真值，因此，DEKF算法在自适应参数调整过程中，波动电流工况与静置工况中对应的模型参数OCVe、Ro、Rp、Tau（RC并联电路的时间常数）存在差异或波动，而无法得到稳定的参数值。而FJKF计算得到的OCVe、Ro、XW没有出现明显的波动现象。由此看出简化阻抗谱模型可以较准确地反映磷酸铁锂电池的动态特性，该模型结合FJKF算法估计得到的参数值稳定性优于一阶RC模型及其参数估计方法。

3.4 参数估计工况适应性分析

为了验证算法的工况适应性，除了FUDS工况测试之外，下文采用FTP75市区和市郊的混合工况测试算法的工况适应性，FTP75市区工况包括冷起动、稳态、热静置和热起动四部分，市郊工况为高速工况。数据系统采集的电池端电压UL和负载电流IL数据以及算法的计算结果如图9、图10所示。

在两种测试工况下，电池模型参数能够迅速跟踪真值，测试工况在热静置、热起动、高速等状态转换时，模型参数值没有出现明显差异或波动，可以稳定反映电池的动态特性。

图9 FTP75工况电压和电流数据Fig.9 FTP75ULandILdata

图10 FJKF算法状态和参数估计值Fig.10 State and parameter estimation result based on FJKF

4 结论

根据动力电池使用工况特性分析、磷酸铁锂电池的电化学阻抗谱特征与等效电路模型对比，本文建立了磷酸铁锂电池的简化电化学阻抗谱等效电路模型，该模型采用分数阶元件——韦伯阻抗元件描述电池的扩散极化特性。

根据已建立的电池简化电化学阻抗谱模型和Grünwald-Letnikov分数阶微分定义，列写了该电池模型离散化形式的状态方程和系统观测方程，采用分数阶联合卡尔曼滤波算法，估算得到磷酸铁锂电池的扩散极化电压、开路电压、欧姆内阻以及扩散极化参数，这些参数可以较准确地反映电池动态特性。

该方法与一阶RC模型和DEKF参数估计方法相比，参数的稳定性高，并且物理意义明确。另外，通过FTP75工况试验可以看出，该方法具有较好的工况适应性。

本文提出的模型参数估计方法有望用于磷酸铁锂动力电池SOC估计、SOP预测、SOH估计等技术中，进而提高电池系统工作过程的安全性、可靠性及有效性。该方法是否能够适用于其他类型锂离子动力电池还需要进一步验证。

[1] 马玲玲, 杨军, 付聪, 等. 电动汽车充放电对电网影响研究综述[J]. 电力系统保护与控制, 2013, 41(3): 140-148. Ma Lingling, Yang Jun, Fu Cong, et al. Review on impact of electric car charging and discharging on power grid[J]. Power System Protection and Control, 2013, 41(3): 140-148.

[2] 高明煜, 何志伟, 徐杰. 基于采样点卡尔曼滤波的动力电池SOC估计[J]. 电工技术学报, 2011, 26(11): 161-167. Gao Mingyu, He Zhiwei, Xu Jie. Sigma point Kalman filter based SOC estimation for power supply battery[J]. Transactions of China Electrotechnical Society, 2011, 26(11): 161-167.

[3] 于海芳, 逯仁贵, 朱春波, 等. 基于安时法的镍氢电池SOC估计误差校正[J]. 电工技术学报, 2012, 27(6): 12-18. Yu Haifang, Lu Rengui, Zhu Chunbo, et al. State of charge estimation calibration for Ni-MH battery based on ampere-hour method[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 12-18.

[4] 刘艳莉, 戴胜, 程泽, 等. 基于有限差分扩展卡尔曼滤波的锂离子电池SOC估计[J]. 电工技术学报，2014, 29(1): 221-228. Liu Yanli, Dai Sheng, Cheng Ze, et al. Estimation of state of charge of lithium-ion battery based on finite difference extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 221-228.

[5] Xiong R, Sun F, He H, et al. A data-driven adaptive state of charge and power capability joint estimator of lithium-ion polymer battery used in electric vehicles[J]. Energy, 2013, 63(12): 295-308.

[6] Andre D, Appel C, Soczka-Guth T, et al. Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries[J]. Journal of Power Sources, 2013, 224(2): 20-27.

[7] 马泽宇, 姜久春, 张维戈, 等. 锂离子动力电池热老化的路径依赖性研究[J]. 电工技术学报, 2014, 29(5): 221-227. Ma Zeyu, Jiang Jiuchun, Zhang Weige, et al. Research on path dependence of large format LiMn2O4battery degradation in thermal aging[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 221-227.

[8] 陈大分, 姜久春, 王占国, 等. 动力锂离子电池分布参数等效电路模型研究[J]. 电工技术学报, 2013, 28(7): 169-176. Chen Dafen, Jiang Jiuchun, Wang Zhanguo, et al. Research on distribution parameters equivalent circuit model of power lithium-ion batteries[J]. Transactions of China Electrotechnical Society, 2013, 28(7): 169-176.

[9] 李国杰, 唐志伟, 聂宏展, 等. 钒液流储能电池建模及其平抑风电波动研究[J]. 电力系统保护与控制, 2010, 38(22): 115-120. Li Guojie, Tang Zhiwei, Nie Hongzhan, et al. Modelling and controlling of vanadium redox flow battery to smooth wind power fluctuations[J]. Power System Protection and Control, 2010, 38(22): 115-120.

[10] 高金辉, 唐静, 贾利锋. 太阳能电池参数求解新算法[J]. 电力系统保护与控制, 2012, 40(9): 133-136. Gao Jinhui, Tang Jing, Jia Lifeng. A novel parameter extraction method for solar cells[J]. Power System Protection and Control, 2012, 40(9): 133-136.

[11] 娄素华, 易林, 吴耀武, 等. 基于可变寿命模型的电池储能容量优化配置[J]. 电工技术学报, 2015, 30(4): 265-271. Lou Suhua, Yi Lin, Wu Yaowu, et al. Optimizing deployment of battery energy storage based on lifetime predication[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 265-271.

[12] Zhang L, Wang L, Hinds G, et al. Multi-objective optimization of lithium-ion battery model using genetic algorithm approach[J]. Journal of Power Sources, 2014, 270(12): 367-378.

[13] Yoon S, Hwang I, Lee C, et al. Power capability analysis in lithium ion batteries using electrochemical impedance spectroscopy[J]. Journal of Electroanalytical Chemistry, 2011, 655(1): 32-38.

[14] Xu J, Mi C, Cao B, et al. A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model[J]. Journal of PowerSources, 2013, 233(1): 277-284.

[15] Fleischer C, Waag W, Heyn H, et al. On-line adaptive battery impedance parameter and state estimation considering physical principles in reduced order equivalent circuit battery models part 1[J]. Journal of Power Sources, 2014, 260(8): 276-291.

[16] Fleischer C, Waag W, Heyn H, et al. On-line adaptive battery impedance parameter and state estimation considering physical principles in reduced order equivalent circuit battery models part 2[J]. Journal of Power Sources, 2014, 262(9): 457-482.

[17] Waag W, Fleischer C, Sauer D. Adaptive on-line prediction of the available power of lithium-ion batteries[J]. Journal of Power Sources, 2013, 242(11): 548-559.

[18] Sierociuk D, Dzielinski A. Fractional Kalman filter algorithm for the states, parameters and order of fractional system estimation[J]. International Journal of Applied Mathematics & Computer Science, 2006, 16(1): 129-140.

[19] Sabatier J, Aoun M, Oustaloup A, et al. Fractional system identification for lead acid battery state of charge estimation[J]. Singal Processing, 2006, 86(10): 2647-2657.

[20] Pei L, Zhu C, Wang T, et al. Online peak power prediction based on a parameter and state estimation for lithium-ion batteries in electric vehicles[J]. Energy, 2014, 66(3): 766-778.

Online Parameter Estimation of a Simplified Impedance Spectroscopy Model Based on the Fractional Joint Kalman Filter for LiFe PO4Battery

Li Xiaoyu Zhu Chunbo Wei Guo Lu Rengui
（School of Electrical Engineering and Automation Harbin Institute of Technology Harbin 150001 China）

Battery modeling and online battery model parameter estimation are the key technologies of EV battery management system. Based on the battery simplified electrochemical impedance spectroscopy which contains a fractional component, this paper establishes the state transition and systematic observation equations for the nonlinear system of LiFePO4secondary battery. Then, the diffusion polarization voltage and model parameters are estimated online with the fractional joint Kalman filter (FJKF). The experimental results show that, this model can reflect the dynamic characteristics very well, and FJKF parameter estimation algorithm can maintain good accuracy. Meanwhile, the method is suitable for a variety of load conditions. The model parameters obtained by this algorithm have good stability.

LiFePO4battery, fractional battery model, electrochemical impedance spectroscopy, fractional joint Kalman filter

TM912

李晓宇 男，1988年生，博士，研究方向为储能系统综合测试与管理技术，电池梯级利用技术。

E-mail: xiaoyu070220202@126.com

朱春波 男，1964年生，教授，博士生导师，研究方向为储能系统综合测试与管理技术、无线电能传输技术。

E-mail: zhuchunbo@hit.edu.cn （通信作者）

国家高技术研究发展计划（863计划）（2012AA111003），国家自然科学基金（51277037）和黑龙江省应用技术研究与开发计划项目（GA13A202）资助。

2014-10-17 改稿日期2015-03-02