涡流式电磁声发射检测声波响应特性

蔡智超刘素贞张 闯杨庆新,2

（1. 河北工业大学电磁场与电器可靠性省部共建重点实验室 天津 300130 2. 天津工业大学电工电能新技术天津市重点实验室 天津 300387）

涡流式电磁声发射检测声波响应特性

蔡智超1刘素贞1张 闯1杨庆新1,2

（1. 河北工业大学电磁场与电器可靠性省部共建重点实验室 天津 300130 2. 天津工业大学电工电能新技术天津市重点实验室 天津 300387）

涡流式电磁声发射检测由于其局部非接触式加载方式，适用于恶劣环境下对金属构件损伤在线检测，同时也是对传统声发射技术的有利补充。针对不同电磁载荷条件下电磁声发射产生的声波响应问题进行深入研究。通过引入电致塑性理论和自由电子运动理论，分析涡流加载下裂纹尖端位错滑移速率变化及声发射能量释放机理，探究不同磁场方向加载下电子的定向移动对声发射响应影响，利用希尔伯特黄变换方法实现对声发射信号的特性分析。实验结果表明：电磁声发射过程中应力波特征与电磁加载条件密切相关。因此，电磁声发射过程为定向移动电子越过障碍势垒产生的特定声波响应。

电磁声发射 电致塑性 自由电子理论 希尔伯特黄变换

0 引言

相比其他无损检测方法，声发射检测方法需对已损构件施加一定的载荷以增加已有缺陷处的活动性，利用缺陷微扩展快速释放的瞬态应力波现象对结构损伤的实际有害程度进行评估。然而对未知损伤构件的在线整体加载而言，目前还存在一定的技术困难及随之而来的经济成本问题，且传统的机械载荷方式还会带来额外损伤。非接触式涡流局部载荷可对构件进行在线检测，且不必对表面进行预处理，定量载荷控制也不会造成额外损伤，是一种经济、安全、可靠的新型声发射检测加载方法[1]。

电磁声发射（Electromagnetic Acoustic Emission, EMAE）技术是传统声发射检测方法的补充，该技术利用电磁激励在缺陷处产生一定的塑性变形，实时对金属裂纹尖端部位快速释放能量所产生的瞬态弹性波进行拾取分析。目前在电磁激励弹性波效应取得了一定的进展：使用脉冲电流、交变涡流等电磁载荷作用于微细裂纹并产生声发射应力波；高频涡流加载下闭合裂纹的非线性动态响应并伴随非线性超声的产生；电磁超声信号检测系统中电磁干扰的消除设计等[1-3]。

本文针对电磁声发射微观机制及微弱声信号特征分析等亟须解决的问题，采用电致塑性及自由电子运动理论深入分析EMAE机理，通过希尔伯特黄变换分析其非线性、非平稳声发射信号等微弱信号特征，为实现电磁声发射技术定量分析及工程探伤应用提供重要的理论及实验基础。

1 电磁声发射机理

1.1 涡流加载电磁声发射特性

涡流的引入是电磁声发射过程的先决条件，给金属材料施加一定条件的电磁激励，将对其流变应力、延伸率、应力松弛、蠕变、裂纹和疲劳产生一定的影响，并促使更多位错出现脱钉、运动及湮灭等现象[4-7]。

1.1.1 涡流加载特性

瞬时高密度电流作为一种附加能量的注入对原子的随机运动产生影响，促进原子的扩散能力，推动位错的运动（滑移、攀移）。这与金属的变形机制有着密切的联系。

高密度电流将增强单位体积自由电子运动动能，从而促使自由电子与其他粒子不规则的碰撞并实现能量传递，进而将产生一系列的位错及增殖[5]，美国学者H. Conrad将定向运动电子与不规则原子排列产生的位错作用定义为电子风力，并将该过程用于解释电致塑性及电致成型加工技术[8-10]。电子风力σew为

式中，σew为单位位错长度下的电子风力；ξew为电子风力系数，由材料的导电特性决定；J为引入的外加电流密度。式（1）表明电子风力与电流密度成正比关系。

除了电子风力，实际上电流激励的引入还包括多物理场问题：电磁、结构和温度之间能量会发生相互转化[11]，该过程将额外引入包括热效应在内的诸多附加因素。由于电磁声发射激励过程所通过的电流时间约为100μs，因温度场引发的热压力远小于电子风力，可忽略该过程的附加效应，微观动应力以电子风力为主。

一般情况下，材料的塑性应变率可表示为

式中，b为伯格矢量的模；为指前因子；σ*为有效应力；σ为流变应力；A*为激活面积，指在单位时间内位错线依靠载荷激活越过障碍所扫过的面积；ΔH0为激活能。当通以电流载荷时，、、σ*、A*和ΔH0将发生改变。进一步可得经过电流加载后塑性应变率ε˙e为[12-14]

式中，下标e表示加载电流载荷之后的变量。

结合式（2）、式（3）可得

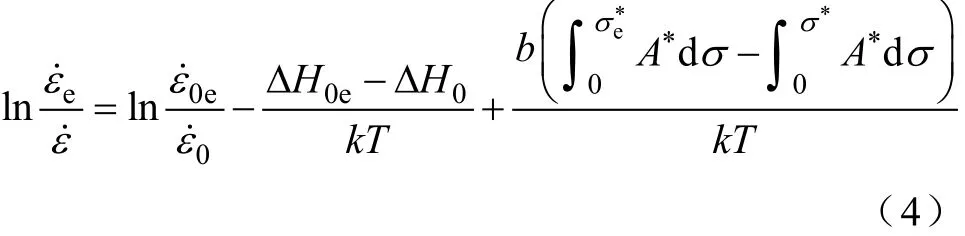
假定残余应力σ*在极小范围内变动，同时引入激活能函数ΔH(σ*)，ΔH(σ*)=ΔH0*-v*σ*，其由激活能、残余应力及激活量v*（v*=kT/(σm)）等受电磁载荷影响的变量组成，m为流变应力对应变速率敏感系数。电磁加载后，ΔHe(σ*)=ΔH*0e-v*e(σ*+σew)，将激活能函数代入式（4），可得

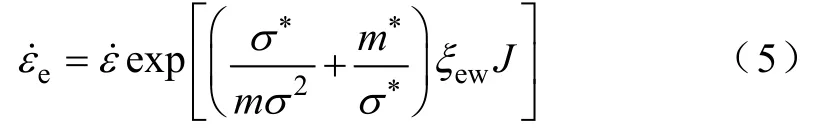
式中，m*为位错滑移速率对应力的敏感系数。

1.1.2 声发射应力波释放

表征材料屈服特性的流变应力可表示为[15]

式中，K为强度系数；n为应变硬化指数。上述方程由Fields-Backofen提出，适用于绝大部分金属材料。由文献[16]知，整体位错密度ρ与流变应力的关系式为[16]

式中，km=μb/(2παs)，μ为剪切模量，对于螺旋位错αs=1，刃形位错αs=1-ν，ν为泊松比。联立式（6）和式（7）可得ρ与ε、ε˙之间的关系为

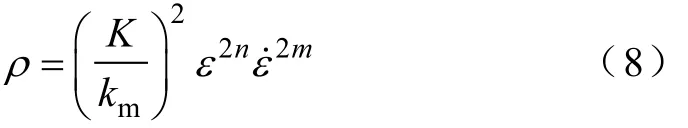
伴随电流激活情况，可动位错密度ρm与整体位错密度比值系数γm将增加，进而可求得可动位错密度与ε、之间的关系为

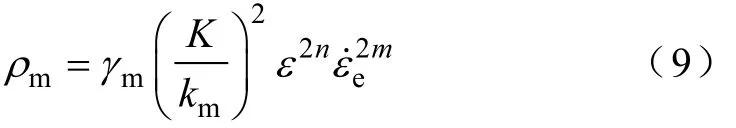
声发射过程中能量的释放是通过可动位错运动产生的，单位体积中单位位错密度运动产生的瞬时能量为

式中，产生声发射效应的应力σe以电子风力为主，在不同构件加载过程中，σe将包含构件中的残余应力。考虑到电流加载的瞬时突发性，在电流持续过程中近似将位错速度ve保持恒定。因此，可动螺旋位错、刃形位错产生的金属声发射过程释放的总能量分别为

其中

式中，ct为金属材料中的横波波速；cl为金属材料中的纵波波速；Se为电流与位错作用的有效面积；δ为趋肤深度。该能量辐射过程始于位错运动的起始时刻t1（并非电流激励的瞬间时刻），结束于电流加载峰值时刻t2（基于声发射凯瑟效应）。

联立式（9）、式（11）和式（12）可看出，大量定向移动的自由电子运动克服位错间的势垒过程，释放一定的能量并伴随声发射应力波的产生。该过程主要受电流密度的影响，随着电流密度的增大，该过程效应逐渐增强。此外，电磁声发射的产生还与电流路径、位错重叠情况及趋肤深度等因素有关。

电磁声发射检测原理如图1所示。通常情况下，裂纹尖端位错密度显著，同时，流经尖端的电流也将重新分配在边界处呈现出显著的集中效应。同等条件下，裂纹尖端比其他区域更易产生声发射效应，因此电磁声发射信号主要依赖于材料已有的位错。

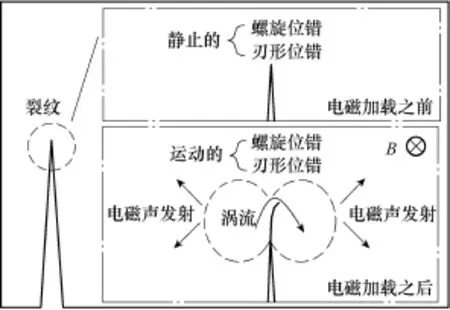
图1 电磁声发射检测原理Fig.1 Principle of electromagnetic acoustic emission detection

1.2 磁场电磁声发射特性

对于引入的磁场，可在晶体中周期场的本征态基础上进一步讨论。通常有两种方法进行演算，即求解含有外加势场的波动方程或把自由电子运动近似当作经典粒子来处理。由于电磁声发射过程中外加磁场为匀强磁场，可选择经典粒子方式处理。

定向移动的自由电子与其他粒子碰撞过程中伴随散射。所获得的场能及时与碰撞的原子交换，即在导体内受电场力作用的自由电子虽保持定向移动但不会保持加速，这与传统真空环境下研究电子的运动规律有所区别。固定方向电场促使导体中电子以定向稳定速度前进。当再引入匀强磁场，可把问题简化为匀速带电粒子在匀强磁场中的运动情况。

当电子的平均速度与磁场方向成任意角度时，该速度可分解为平行于磁场方向速度径向分量及垂直于磁场方向的速度轴向分量。径向速度使电子作圆周运动，而轴向分量使电子平移。在两个速度分量的综合作用下，电子将按螺旋形轨迹前进。预设漂移电子的速度方向与磁场方向夹角为θ，粒子作螺旋形轨迹运动的半径为

式中，me为电子质量；ve为电子速度；e为电荷量；B为磁场强度。

自由电子所做螺旋形轨迹的螺间距为

图2是不同磁场方向下的自由电子轨迹。假定自由电子运动方向为x方向，施加不同方向的磁场（箭头方向表示），将直接影响电子螺旋形运动的半径及螺间距。因此，磁场的加载情况将影响自由电子与运动轨迹上障碍势垒的碰撞过程。

图2 不同磁场方向下的自由电子轨迹Fig.2 Electron trajectories under different directional magnetic field

由于运动轨迹的变化直接影响自由电子与位错之间的碰撞过程，式（1）中电子风力在实际作用过程需考虑伯格矢量与电子运动矢量的相对角度，基于虚功原理，仅当两者存在一定角度时（非直角）才存在有效作用。因此，该过程使得电致塑性中所传递能量产生差异，从而影响声发射应力波的释放。

2 电磁声发射实验

本文设计两种电磁声发射激励探头：其中一种为提供垂直静磁场的矩形永磁体及螺旋线圈，另一种为提供平行静磁场的U形永磁体及螺旋线圈。试件为0.3m×0.06m×0.001 3m的3A21薄型铝板。其中，薄板边缘通过线切割制作3mm预制裂纹，并采用高频疲劳实验机在5kN、77.7Hz交变载荷条件下经17 500次循环周期制作成长约2.45mm的疲劳拉伸裂纹。

激发系统采用RITEC公司RPR-4000功放、高频阻抗匹配激励及电磁声发射换能器。采集系统采用美国物理声学公司PCI-2采集卡、宽频（0～1MHz）WSA压电传感器。电磁声发射实验系统如图3所示。传统薄铝板声发射频带在0～600kHz之间，为区分电磁加载过程中产生的超声弹性波，通过施加（＞600kHz）激励电流，并设定接收系统模拟滤波器为0～600kHz，以确保仅接收声发射信号。

图3 电磁声发射实验系统Fig.3 High-current pulse of EMAE experiment system

电磁声发射螺旋状激励线圈采用柔性印制电路板制备，EMAE探头激励示意图如图4所示。螺旋激励线圈产生的涡流场分布均匀且不受裂纹指向的影响，更易在裂纹尖端产生电流集中现象。分别采用U形永磁体提供水平方向的磁场，如图4a所示；矩形状磁体提供垂直方向的磁场，如图4b所示；而无外加磁场作用，仅剩螺旋线圈交变磁场作用如图4c所示。

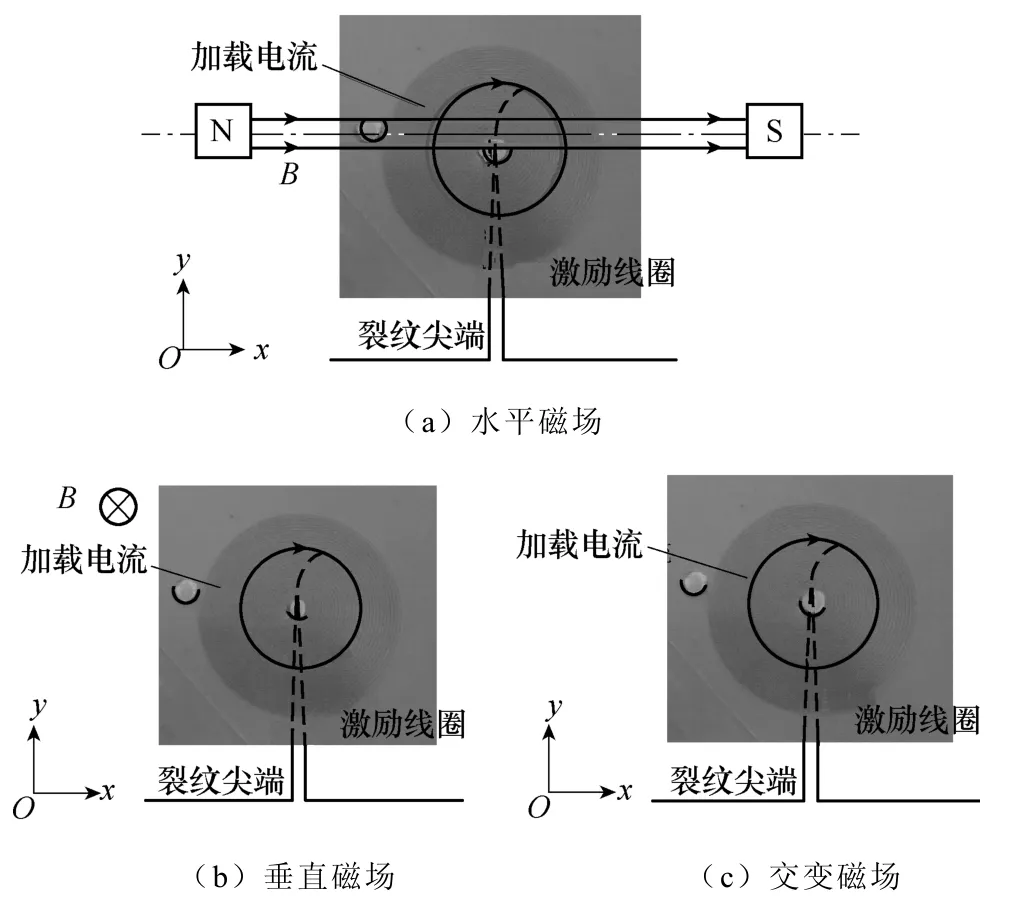
图4 EMAE探头激励示意图Fig.4 Schematic diagrams of EMAE transducer

3 实验

3.1 涡流加载条件

实验加载电流频率范围为700kHz～1MHz，步长为50kHz，电流幅值范围为10～80A，步长为10A。对比分析不同磁场加载条件下的声发射情况。利用声发射信号特征参数进行与加载条件的联立分析，选用能反映声发射相对能量和强度的能量计数，两者关系如图5～图7所示。

图5为交变磁场加载EMAE能量计数，该过程仅有正弦电流激励，无外加静磁场影响，声发射能量计数随电流的增大呈现明显的上升趋势。在相同电流加载条件下随着频率的增大，对应的涡流分布更集中，因此，趋肤深度上层自由电子内越过单向障碍势垒的几率更大。而同样激励幅值的低频载荷，由于涡流相比更为分散，其单向越过障碍势垒的几率更小且产生的声发射效应无前者显著。

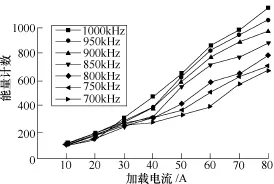
图5 交变磁场加载EMAE能量计数Fig.5 Energy count of EMAE signal under alternating magnetic field

图6、图7分别为垂直和水平静磁场加载EMAE能量计数，可见电流幅值与能量计数成正比。与交变磁场加载相比，垂直磁场加载使自由电子在整个趋肤深度内螺旋运动，趋肤深度越深将有助于增强电子与趋肤深度内障碍势垒的碰撞，产生的能量计数可弥补电流密度分散导致的单向越过障碍势垒几率的减小。因此，垂直磁场加载时，电磁声发射能量计数在低频下产生的能量更高。

水平磁场加载时，由于磁场方向与裂纹指向垂直，因此裂纹尖端两侧的电流与水平静磁场方向垂直，该区域电子将作螺旋运动。而裂纹尖端处产生的绕流方向将于水平静磁场方向保持一致，即在该处电子移动将不受影响。因此，水平磁场加载综合汇聚了交变磁场及垂直磁场加载下EMAE能量计数的特点，其将不受电流频率加载的影响。

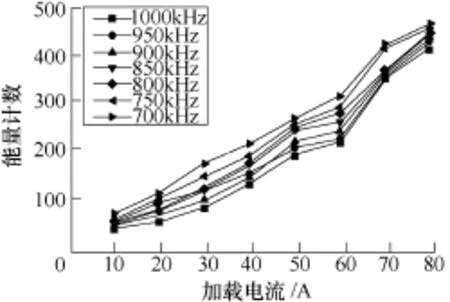
图6 垂直磁场加载EMAE能量计数Fig.6 Energy count of EMAE signal under vertical magnetic field

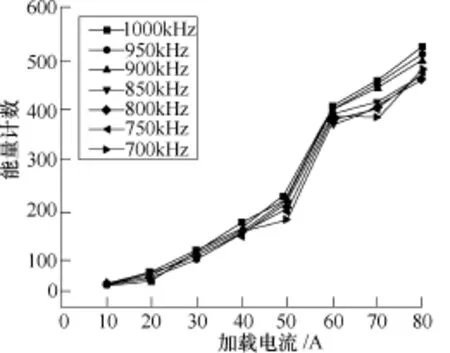
图7 水平磁场加载EMAE能量计数Fig.7 Energy count of EMAE signal under horizontal magnetic field

3.2 电磁声发射信号时域分析

希尔伯特黄变换（Hilbert-Huang Transform, HHT）适于非线性、非平稳瞬态电磁声发射信号的时频分析，增强时频集聚性、降低频谱能量泄漏的同时提高了时频分辨率。HHT方法首先对声发射信号进行经验模式分解，进而将信号表示为有限个本征模态函数及一个残余分量，最后通过HHT对各分解进行瞬态频率的求解。

运用HHT对同电流、不同方向磁场加载条件下电磁声发射信号进行分析，信号中95%以上的能量集中于本征模态函数（Intrinsic Mode Function, IMF）IMF1～IMF5分量，所以着重考察该5个分量。实验不同磁场加载下，电磁声发射信号前5个IMF分量能量比值对比，如图8所示。不同磁场加载下IMF分量的能量比值差异显著，尤其是中心频段为220kHz的IMF1分量与中心频段为100kHz的IMF3分量最显著。

图8 不同磁场加载下IMF1～IMF5分量的能量比值Fig.8 Energy percentage of IMF1～IMF5components under different magnetic field

磁场加载方向除影响主频段分量的能量外，还影响低频段能量分布。以频段在5～50kHz范围内IMF5分量为例，IMF5分量HHT时域图如图9所示。从图9中可以看出，电子与低频段势垒碰撞的声响应瞬时频率在时间轴上离散显著，呈现出特征势垒被作用下频率能谱分散特点，因此其并不具有弹性波时频图中瞬时频率保持连续的特点；所克服势垒瞬时频率都主要集中在0～1ms范围内，符合铝制试件突发性声发射信号持续时间特征；不同的电磁加载其瞬时频谱有较大的区别，环境磁场作为唯一变量，影响自由电子运动轨迹并改变其与障碍势垒碰撞作用，克服障碍势垒所释放的能量将发生一定的改变。据此进一步说明电磁声发射能量、信号特征与磁场加载条件密切相关。

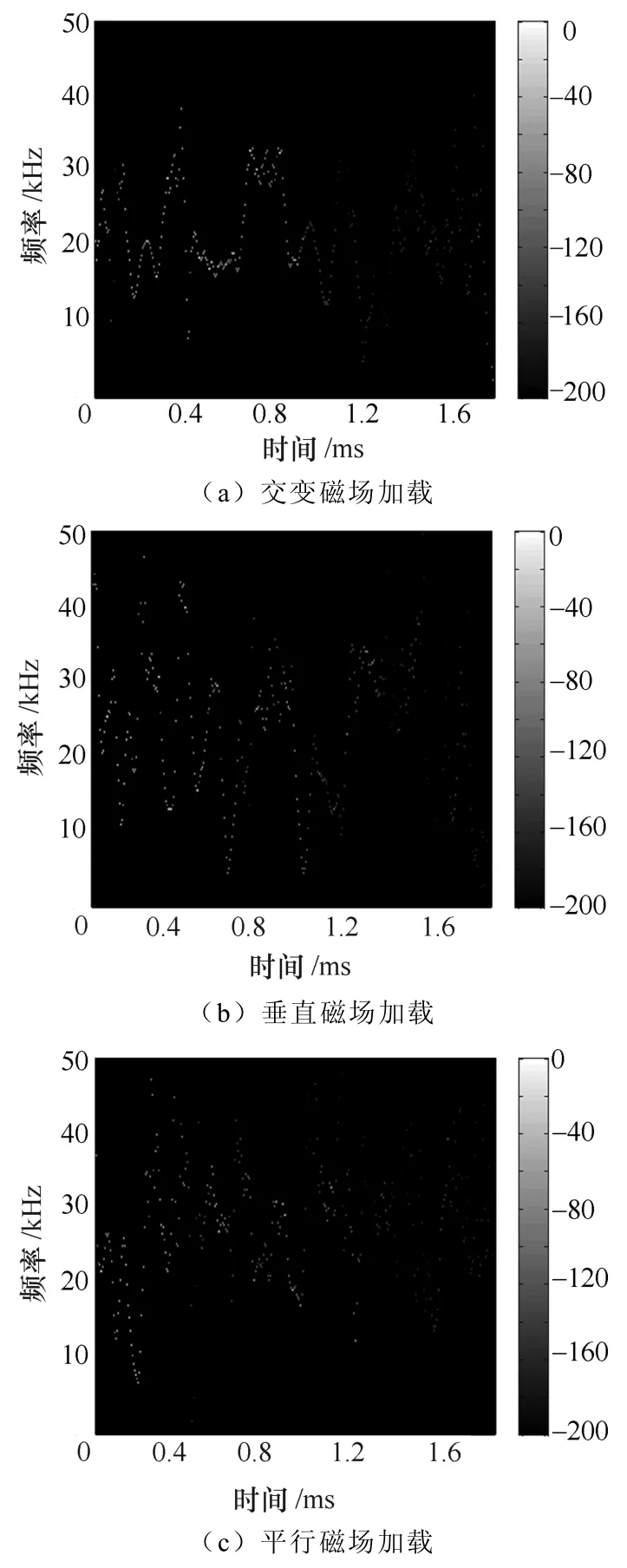
图9 IMF5分量HHT时域图Fig.9 Waves in time domain of IMF5using HHT algorithm

4 结论

本文分析了电磁声发射的产生机制，通过位错滑移动力学推导出考虑金属电子风力效应的位错滑移速率及能量释放方程，基于自由电子理论探究了磁场方向对于电磁声发射能量的影响，从电致塑性、塑性能量释放、磁致轨迹等分析电磁载荷下声发射应力波释放情况，并利用希尔伯特黄方法对不同电磁载荷声发射信号特征进行分析。主要结论如下：

1）涡流式电磁声发射是由注入了改变金属构件塑性应变率的电磁能，产生了电子风力，进而增强可动位错数量，实现自由电子下位错运动并伴随能量释放，进而以声发射声波响应效应完成能量分配的过程。

2）不同方向磁场主导着自由电子的定向移动，改变大量漂移电子推动已有位错越过障碍势垒的方向，从而产生不同的声响应效应。

3）定向漂移电子与位错之间的能量转换是产生电磁声发射效应的必要条件，可通过HHT方式对电磁声发射微小信号进行提取分析，磁场载荷还影响声发射的时频特征。后续工作是利用该方法与机理模型结合以实现裂纹指向性评价。

[1] 张闯, 刘素贞, 金亮, 等. 基于大电流直接加载的电磁声发射试验[J]. 电工技术学报, 2013, 28(1): 101-105. Zhang Chuang, Liu Suzhen, Jin Liang, et al. Experimental study of electromagnetically induced acoustic emission based on high current loading directly[J]. Transactions of China Electrotechnical Society, 2013, 28(1): 101-105.

[2] 刘素贞, 庄东超, 商士博, 等. 高频涡流加载下闭合裂纹的动态响应特征[J]. 电工技术学报, 2015, 30(18): 246-252. Liu Suzhen, Zhuang Dongchao, Shang Shibo, et al. Dynamic response characteristics of closed crack with the high frequency eddy current loading[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 246-252.

[3] 刘素贞, 李丽滨, 蔡智超, 等. 电磁超声检测系统中消除电磁干扰电路的设计[J]. 电工技术学报, 2016, 31(1): 80-84. Liu Suzhen, Li Libin, Cai Zhichao, et al. The design for electromagnetic interference eliminating circuitsin electromagnetic ultrasonic testing systems[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 80-84.

[4] Lei G, Tang G, Paul K C. Recent advances and challenges in electroplastic manufacturing processing of metals[J]. Journal of Materials Research, 2010, 25(7): 1215-1224.

[5] Molotskii M I. Theoretical basis for electro- and magnetoplasticity[J]. Materials Science and Engineering, 2000, 287(2): 248-258.

[6] Golovin Y I. Magnetoplastic effects in solids[J]. Physics of the Solid State, 2004, 46(5): 769-803.

[7] Alshits V I, Darinskaya E V, Koldaeva M V, et al. Magnetoplastic effect in nonmagnetic crystals[M]. North Holland: Elsevier, 2008.

[8] Sprecher A F, Mannan S L, Conrad H. Overview no. 49: on the mechanisms for the electroplastic effect in metals[J]. Acta Metallurgica, 1986, 34(7): 1145-1162.

[9] Conrad H. Thermally activated plastic flow of metals and ceramics with an electric field or current[J]. Materials Science and Engineering A, 2002, 322(1-2): 100-107.

[10] Antolovich S D, Conrad H. The effects of electric currents and fields on deformation in metals, ceramics, and ionic materials: an interpretive survey[J]. Materials and Manufacturing Processes, 2004, 19(4): 587-610.

[11] 付宇明, 王俊丽, 郑丽娟. 含埋藏裂纹构件脉冲放电相变应力分析[J]. 中国机械工程, 2014, 25(8): 1117-1121. Fu Yuming, Wang Junli, Zheng Lijuan. Analysis on phase transformation stress after pulse current discharging of metal component with buried crack[J]. China Mechanical Engineering, 2014, 25(8): 1117-1121.

[12] Li D, Yu E, Liu Z. Microscopic mechanism and numerical calculation of electroplastic effect on metal's flow stress[J]. Materials Science and Engineering A, 2013, 580: 410-413.

[13] Li D, Yu E. Computation method of metal's flow stress for electroplastic effect[J]. Materials Science and Engineering A, 2009, 505(1): 62-64.

[14] Chandra B P, Anubha S G, Chandra V K, et al. Dislocation unpinning model of acoustic emission from alkali halide crystals[J]. Indian Academy of Sciences, 2004, 62(6): 1281-1292.

[15] Gronostajski Z. The constitutive equations for FEM analysis[J]. Journal of Materials Processing Technology, 2000, 106(1): 40-44.

[16] Chung J B, Asibu E K. Acoustic emission from plastic deformation of a pure single crystal[J]. Journal of Applied Physics, 1992, 72(5): 1812-1820.

Acoustic Response Characteristics of Acoustic Emission Induced by Eddy Current Exciting

Cai Zhichao1Liu Suzhen1Zhang Chuang1Yang Qingxin1,2
（1. Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China 2. Key Laboratory of Advanced Electrical Engineering and Energy Technology Tianjin Polytechnic University Tianjin 300387 China）

Due to the contactless local loading of electromagnectic acoustic emission, this paper provides a method for the damage online inspection under severe working conditions, which is a beneficial supplement of traditional acoustic emission technology. This paper studies the acoustic response characteristics arising from electromagnetic acoustic emission under various electromagnetic loads. According to the electroplastic theory and free-electron theory, the mechanism of acoustic emission energy release and the rate variations of the crack tip dislocation slip are analyzed. Thus, the various acosutic responses of the electronic directional movement under different magnetic field directions can be obtained. The electromagnetic acoustic emission signal analysis based on Hilbert-Huang transform (HHT) is an effective tool to extract the features. The experimental results show the stress wave characteristics are closely related to electromagnetic loading. Therefore, this process is the specific acoustic response between the directional mobile electronic and obstacle barrier.

Electromagnetically induced acoustic emission, electroplastic, free-electron theory, Hilbert-Huang transform

TM153

蔡智超 男，1989年生，博士，研究方向为电磁无损检测技术。

E-mail: czchebut@foxmail.com

刘素贞 女，1969年生，教授，博士生导师，研究方向为工程电磁场与磁技术。

E-mail: szliu@hebut.edu.cn（通信作者）

国家自然科学基金（51307043），河北省自然科学基金（E2016202260）和天津市自然科学基金（16JCYBJC19000）资助项目。

2015-07-30 改稿日期 2016-01-23