基于分形理论的SF6/N2混合气体放电仿真

李 敏汪 沨许松枝陈晓林黄墀志谢望君

（1. 湖南大学电气与信息工程学院 长沙 410082 2. 长沙供电公司 长沙 410000）

基于分形理论的SF6/N2混合气体放电仿真

李 敏1,2汪 沨1许松枝1陈晓林1黄墀志1谢望君1

（1. 湖南大学电气与信息工程学院 长沙 410082 2. 长沙供电公司 长沙 410000）

为了研究SF6/N2混合气体电介质击穿现象，利用编写的Matlab程序对放电通道发展过程进行数值模拟，并结合分形几何原理计算放电树枝的分形维数。基于分形理论，建立了考虑空间电荷分布和引入物理时间的棒-板分形放电仿真模型，通过有限元方法（FEM）计算空间电场，并首次结合通量校正传输（FCT）法求解带电粒子连续性方程，研究了不同发展概率指数、不同放电阈值和SF6含量变化下分形放电特性。结果表明：概率指数越大，SF6含量越高，则分形维数越小，放电树枝分叉也越少；体积含量50%/50%的SF6/N2混合气体放电分形维数D=1.219 2，整个放电过程流注发展平均速度为1.15Mm/s，并得到了不同时刻空间电荷及轴向电场与电子浓度的分布。

放电 分形维数 SF6/N2混合气体 有限元方法 通量校正传输法 概率指数

0 引言

目前，关于SF6/N2混合气体流注放电的仿真研究比较多，其放电机理、绝缘性能和电晕放电特性成为研究热点[1-3]。现有的放电模型主要是针对放电后电晕形成和流注发展，没有从微观上很好地解释流注放电通道的形成过程。分形的概念最早由B. B. Mandelbrot[4]于1975年提出，它是一种用于研究和处理自然界与工程应用中不规则图形的强有力工具。SF6气体放电击穿现象非常复杂，放电过程会产生一些细小的放电通道，且放电通道明显呈现出树枝状的特征，有一定的随机特性和自相似特性[5]。因此可以采用分形几何的方法来研究SF6气体放电发展过程[6,7]。

研究绝缘介质分形放电特征的模型主要有两种，即NPW模型[8]和WZ模型[9]。NPW模型中只考虑电场强度E和发展概率分布函数中的概率指数η，放电树枝的发展只沿着电场最大的方向发展，即发展方向很固定。而WZ模型在NPW模型基础上引入放电阈值EC和放电通道电压降ΔU，其发展结果更接近实际情况。无论是NPW模型还是WZ模型均未考虑空间电荷和局部放电对放电通道的影响，而实际中空间电荷对放电通道有明显影响。俄罗斯学者D. I. Karpov和A. L. Kupershtokh在NPW模型基础上引入空间电荷，并考虑杂质对放电结构的影响，提出了一种不均匀绝缘体系中放电生长的NKL模型[10]，完善了分形电介质放电仿真。2005年，H. Z. Ding和 B. R. Varlow提出了一种同时考虑电场和机械应力的电树生长热动力学模型[11]，使得分形放电的研究进入到一个更深入的阶段。贺恒鑫等建立了结合传统流注放电理论和分形生长理论的正极性流注生长概率模型[12]，研究了棒-板长间隙正极性流注放电过程。2012年，山东大学的谭震宇结合分形理论构建了考虑气泡生长过程的水中流注放电仿真模型[13]，并对不同电压幅值和溶液电导率下的放电特性进行仿真。2013年，重庆大学的陈伟根基于多重分形特征研究了绝缘子污秽放电过程，得出泄漏电流波形的广义分形维数和多重分形谱宽能有效预测污秽放电的发展趋势[14]。

本文在总结现有分形电介质放电模型的基础上，考虑了空间电荷对放电通道的影响（即在放电初始时刻先在棒头部释放一定种子电子，电子在电场力的作用下向极板运动，同时与中性混合气体发生碰撞电离，产生新的电子、正离子和负离子，从而使放电间隙逐渐分布空间电荷），引入阈值电场、物理时间（每一步平均发展时间Δt）和通道电压降落ΔU等参数，并结合泊松方程和带电粒子连续性方程描述放电通道内部的电荷转移。阐述了如何结合分形计算SF6/N2混合气体；说明了分形放电初始条件的设置。本文首次采用有限元通量校正传输算法对不同浓度SF6/N2混合气体分形放电过程进行仿真分析。通过有限元方法（Finite Element Method, FEM）准确求解泊松方程，通量校正传输法（Flux Corrected Transport, FCT）计算空间带电粒子浓度的变化。该模型不仅可以直接给出分形放电发展的动态演化，还可以给出放电分形维数、流注发展速度等微观参数。

1 分形放电的数学模型

1.1 放电树枝的分形维数计算

由于气体放电通道的发展呈树枝状，并且放电树枝在一定尺度内具有很强的自相似，定量分析放电树枝时需用到分形的概念。图1为SF6气体分形放电图像[8]。根据分形几何学，放电树枝总长度与放电单位长度的关系满足[7]

式中，D为分形维数；N(r)为放电树枝总长度；r为单位长度，r=1/R，R为放电半径。由式（1）得

当R与r相比足够大时，由式（2）可得到放电树枝的分形维数。

1.2 空间电场和带电粒子连续性方程离散求解

气体放电过程的产生和发展是一个非常复杂的过程，包括分子、电子、正负离子的电离、复合、附着、迁移、扩散、光电离等过程，可以采用带电粒子连续性方程与泊松方程式（3）～式（5）描述[15,16]。空间各点的电位φ通过求解泊松耦合方程给出，即

式中，ρ为空间电荷密度；εr和ε0分别为混合气体介质相对和真空介电常数；E为电场强度；e为基本电荷；Nx为带电粒子浓度（其中包括电子浓度Ne、正离子浓度N+和负离子浓度N-）；νx、Dx和Sx分别为粒子迁移速率、扩散系数和粒子源项（包括电离、吸附及复合过程），它们都是电场强度与中性混合气体浓度比值（E/N）的函数[3]。

为了提高计算精度，本文采用FEM求解式（3），准确地给出各个节点的电位。并通过式（4）计算出空间各点的场强。在放电通道内存在大量带电粒子的迁移运动，粒子浓度变化非常快，对式（5）先采用两步泰勒-迦辽金格式[17]，每发展一步在时间上进行离散得到式（6），再对式（6）利用经典的迦辽金加权余量法[18]得到矩阵方程（7）。

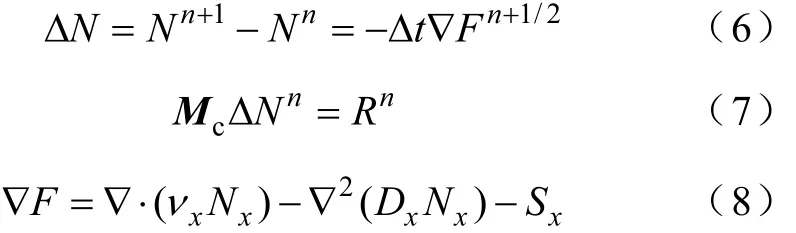
式中，Mc为单元贡献一致质量矩阵[19]；Rn为单元对节点的贡献量；ΔN为节点粒子浓度增量；Δt为时间步长。式（7）采用高精度的FCT进行求解[20,21]，可以有效地抑制仿真过程出现的数值扩散问题。

1.3 分形放电树枝发展机制

为了更好地对SF6/N2混合气体放电进行模拟，本文结合分形理论，从分形放电的角度研究其放电特性及流注发展机理。不同混合气体比例SF6/N2，其耐电强度（即击穿场强）不同，主要通过放电阈值Ec决定。只有当放电通道内场强高于放电起始场强时，才能产生有效电离，并保证放电往前发展。SF6/N2混合气体中粒子的迁移率、电离率、吸附率、复合率等参数都是场强与中性混合气体浓度比值（E/N）的函数。而概率指数选择和每一步发展时间Δt都与空间电场E有关。放电树枝各方向发展的概率由各方向的有效碰撞电离系数决定，本文采用WZ模型的发展概率函数[9]，即

式中，η为放电发展的概率指数；Ei为待发展节点i处的场强。η和Ei分别表示随机因素和确定性因素对放电发展的影响。从式（9）可以看出放电树枝沿各个方向发展的概率最终是由树枝端部的局部场强和放电阈值决定的。在分形介质击穿模型中，放电通道的发展是由确定的概率分布决定的，因此考虑通过概率分布转换得到“物理时间”[22]，本文采用文献[23]中的方法，根据式（9）确定的概率函数，放电通道某一点的生长率函数为。由于放电通道内各个发展点在统计上是独立的，故总生长率G是所有可能发展方向上的生长率总和，则每一步平均发展时间Δt为G的倒数，即

式中，θ为时间转移系数，其值与气体介质放电特性和具体的放电发展过程有关；Δt为时间步长，取值与此处的每一步平均发展时间相同，即分形放电在每一步发展过程中都是与发展概率函数和放电阈值相关。考虑放电通道内部的电压降落，树枝端部的电位为

式中，φ0为棒头部施加的电压；Li为端部新发展的树枝长度；φi为树枝端部电位。

2 仿真

2.1 分形放电过程

仿真过程：①通过给定初始边界条件，采用FEM求解泊松方程，获得各节点的电位和场强；②利用FCT求解带电粒子连续性方程给出空间各点的粒子浓度；③计算各个待发展点的发展概率，采用累积概率的方法选择待发展点，并将新发展点与已发展点连接；④每发展一步，利用式（11）计算树枝端部电位，并把新发展点的电位计入边界条件中；⑤判断树枝是否发展到极板，若没有返回①步；⑥计算该放电图形的分形维数，放电过程结束。

本文采用如图2所示的棒-板结构电极，对整个区域采用三角元剖分，剖出3 871个节点和7 498个三角单元，黑色实线为已发展的放电树枝。仿真中棒-板间距d=5mm，棒的半径r=0.125mm，棒头部施加电压φ0=-20kV，极板电位φ1=0，棒-板间隙充满标准大气压下的体积含量50%/50% SF6/N2混合气体，温度取300K，混合气体浓度为2.467×1025/m3，放电场强阈值为Ec=343Td（1Td=10-21V·m2），概率指数η=1.0。在t=0ns时，在棒头部附近处释放一定量的初始种子电子，电子的分布为高斯分布[24]，即

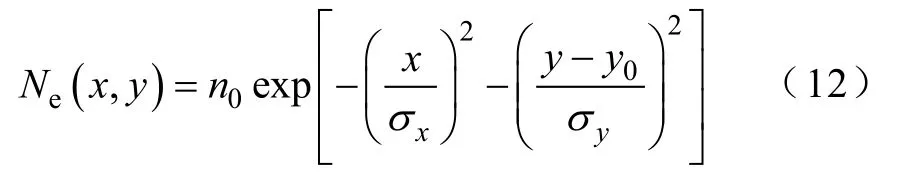
式中，n0=106/cm3；σx=0.1mm；σy=0.05mm；y0=r。

初始电子受电场力作用开始向极板快速运动，电子与中性气体分子发生碰撞电离产生新的电子和正离子，同时电子被SF6气体分子吸附形成负离子。当有效电离系数时，其中，α为电子碰撞电离系数，β为电子吸附系数，才有可能保证分形放电向前发展，流注发展条件为[5]

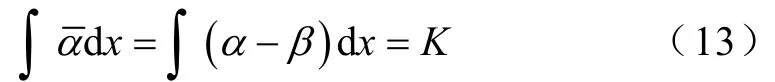
式中，K为常数。

故放电产生和发展的条件为放电通道内场强高于放电起始场强阈值Ec。

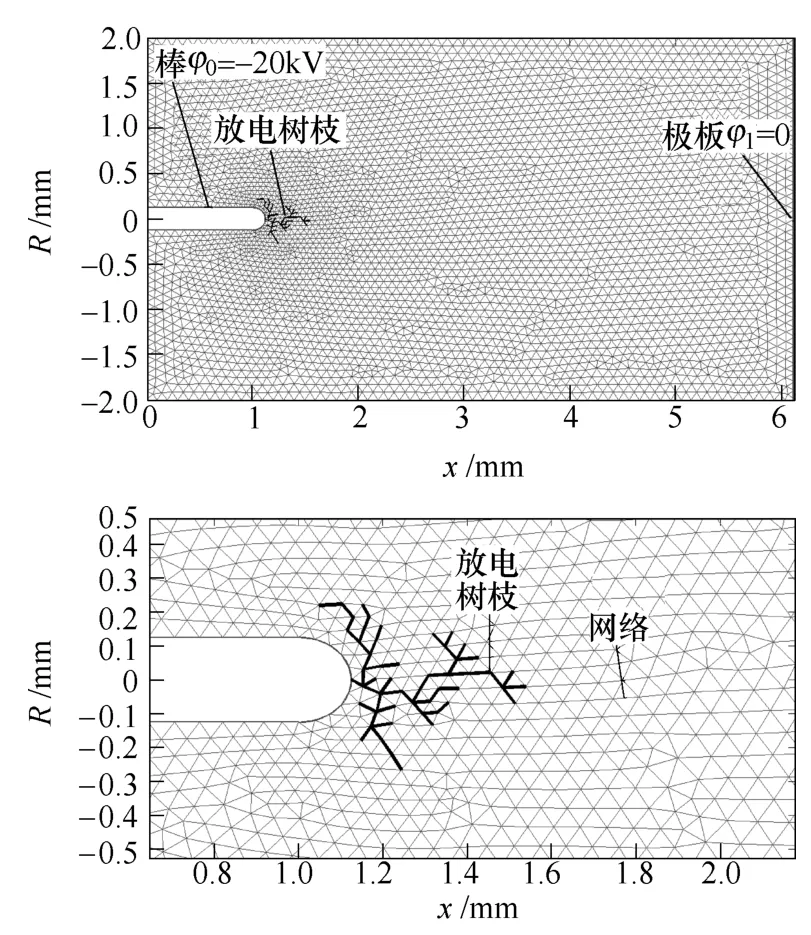
图2 棒-板电极结构剖分及放电树枝Fig.2 Split and discharge branches rod-plane electrode

放电过程采用步进式方式，每一个已发展点可以向周围若干个非树枝点发展，具体发展哪一个点由发展概率函数决定。仿真得到了一次放电过程四个不同时刻的放电图像，如图3所示。空间电荷在放电通道内的主要分布如图4所示。从仿真结果可知，放电开始阶段，流注的发展速度很慢，电树枝在棒头部周围缓慢生长，但棒头部附近起始场强较大，电子与中性粒子发生剧烈的碰撞电离，产生大量新的电子和正离子。同时SF6气体具有较强的吸附作用，一部分电子被其吸附形成负离子，从而空间电荷主要分布在棒头部和流注头部附近。当电树枝发展到一半间隙时，由于放电通道内电离出足够的电子、正离子和负离子，使流注迅速发展，主放电树枝向极板快速发展，直至达到极板，流注发展速度最终达到2.12Mm/s，放电过程结束。整个放电过程流注发展平均速度为1.15Mm/s，得到放电图像的分形维数D=1.219 2。

图3 不同时刻的仿真放电图像Fig.3 Simulation discharge images at different times

图4 不同时刻的仿真空间电荷密度分布Fig.4 Simulation charge density distribution in space at different times

图5为相同条件下，只改变放电发展概率指数得到的仿真结果，图5a、图5b分别为η=0.5、η=1.5时的分形图像。比较分形图像可以看出，放电概率指数越大，放电图像的侧向树枝分叉越少，有明显的主放电树枝。这也表明，当η较大时，放电树枝的发展基本趋向于场强最大的方向，阈值电场对放电树枝影响减小，导致两种情况下得到的分形维数差值增大。

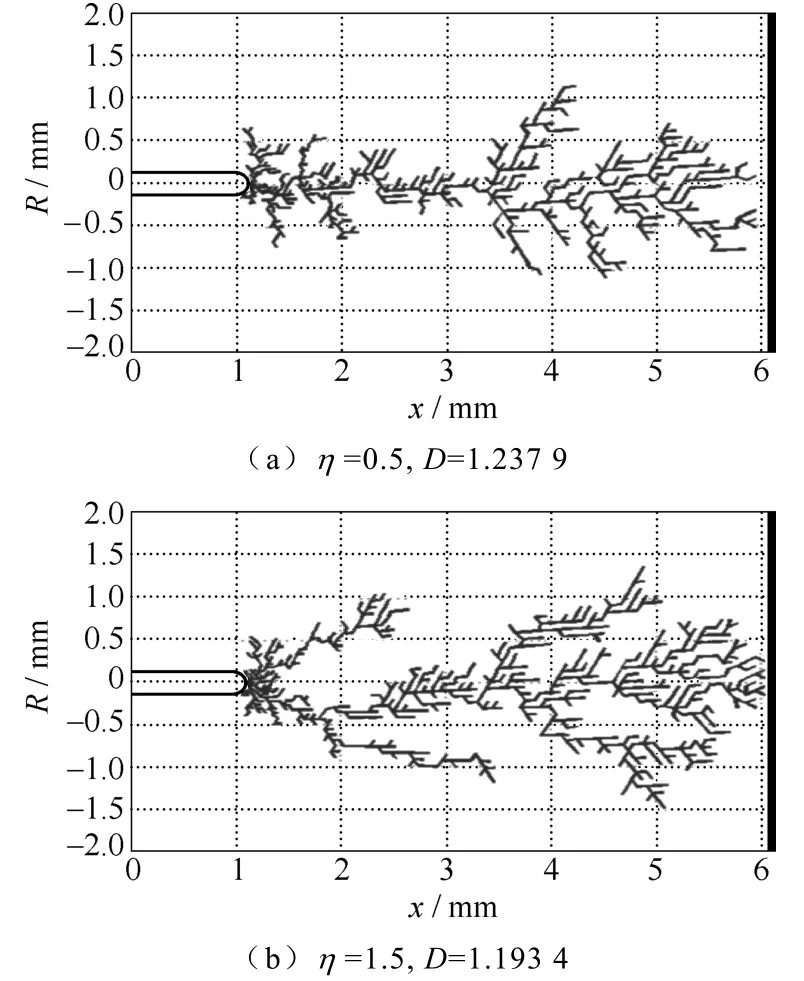
图5 不同放电发展概率指数下的仿真分形图像Fig.5 Fractal images at differentη

图6为相同条件下，通过设置不同放电阈值仿真计算得到的分形维数。由图可知分形维数与放电阈值呈非线性下降关系。放电阈值越大，放电树枝侧向发展概率越小，分形维数也越小；当放电阈值小于343Td时，分形维数增大很快。从式（9）分析可知，放电阈值越小，可供新发展的节点越多，故侧向树枝发展增多，从而使分形维数增大。

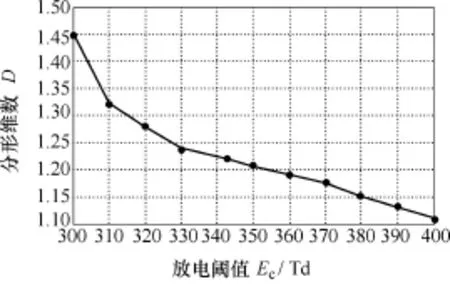
图6 分形维数与放电阈值的关系Fig.6 The relationship between fractal dimension and discharge threshold

图7和图8分别为相同条件下的不同时刻的轴向电场和轴向电子浓度分布。由图7可知，随着放电的发展，轴向场强的峰值逐渐往前移动，这与图3中出现明显的主放电树枝相吻合。另外棒头部附近场强始终较大，是因为头部曲率较大，电场畸变大，一直能产生有效电离。由图8可见，电子浓度峰值随着放电进行，不断迁移且峰值逐渐增大，在放电结束时达到最大值。结合图7可知分形流注头部场强畸变严重，往往是电离最剧烈的区域，因此电子浓度在不断增大。

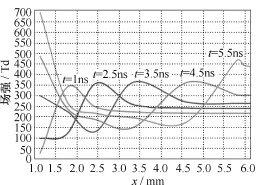
图7 轴向场强分布Fig.7 Electric field distribution along axis

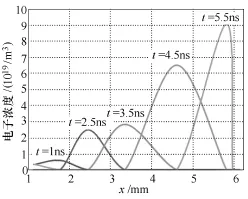
图8 轴向电子浓度分布Fig.8 Electronics density distribution along axis

2.2 分形维数与SF6浓度的关系

保持其他条件不变的情况下，改变混合气体中SF6比例，对SF6/N2中SF6体积含量分别为10%和100%两种情况的放电过程进行仿真分析。放电阈值根据气体间隙耐电强度峰值（即混合气体放电产生有效电离率所需最小场强值）来确定[25]。其中低含量SF6的分形放电过程，放电场强阈值Ec=273Td；纯SF6的分形放电过程，放电场强阈值Ec=377Td。图9a为低含量SF6时的分形图像，D=1.294 5；图9b为纯SF6时的分形图像，D=1.132 2。对比结果发现SF6含量越高，放电树枝侧向分叉越少，分形维数越小，出现明显的主放电树枝。这是由于SF6含量越高吸附系数越大，产生碰撞电离所需场强也越大，同时产生有效放电的场强阈值也提高。并且SF6气体分子具有较强的吸附作用，通道中的电子很容易被SF6气体分子吸附变成负离子，使主放电通道内离子数量增加，导致流注头部场强畸变很大，故放电树枝不易往两侧发展。

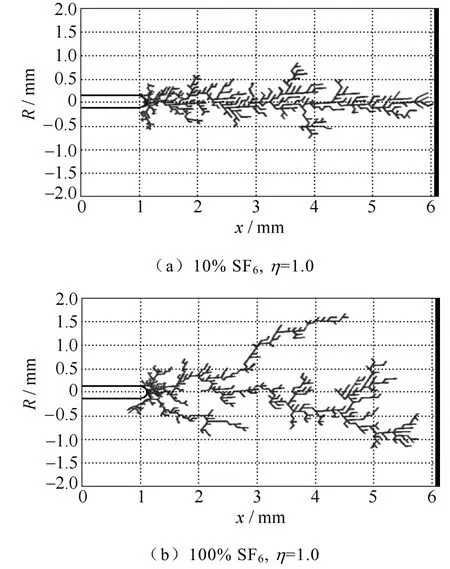
图9 不同SF6含量下的分形图像Fig.9 Fractal images at different percentages of SF6

3 结论

1）本文提出的模型能够很好地模拟SF6/N2混合气体分形放电过程，得到了完整的分形图像、分形维数和流注发展速度。

2）仿真结果表明，概率指数和SF6气体比例越大，放电侧向树枝分叉越少，有明显的主放电树枝；概率指数越大的一侧向放电树枝的发展概率越小，而SF6浓度越高吸附作用越强。

3）仿真也得到了不同时刻空间电荷分布、轴向电场分布及轴向电子浓度分布等微观参数，可以更好地从微观角度理解SF6/N2混合气体的放电机理。

[1] 汪沨, 肖晓林, 张宪标, 等. 基于PIC法SF6/N2混合气体中绝缘子沿面放电特性研究[J]. 电工技术学报, 2011, 26(8): 220-226. Wang Feng, Xiao Xiaolin, Zhang Xianbiao, et al. Research on the insulator surface discharge characte-ristics in SF6/N2gas mixture using PIC method[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 220-226.

[2] 赵虎, 李兴文, 贾申利. SF6及其混合气体临界击穿场强计算与特性分析[J]. 西安交通大学学报, 2013, 47(2): 109-115. Zhao Hu, Li Xingwen, Jia Shenli. Calculation and characteristic analysis of critical breakdown field strength of SF6and the mixtures[J]. Transactions of China Electrotechnical Society, 2013, 47(2): 109-115.

[3] 汪沨, 李锰, 潘雄峰, 等. 基于FEM-FCT算法的SF6/N2混合气体中棒-板间隙电晕放电特性的仿真研究[J]. 电工技术学报, 2013, 28(9): 261-267. Wang Feng, Li Meng, Pan Xiongfeng, et al. Corona discharge simulations of rod-plate gap in SF6/N2gas mixtures using FEM-FCT method[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 261-267.

[4] Mandelbrot B B. The fractal geometry of nature[M]. New York, USA: W. H. Freeman and Company, 1982.

[5] 陈庆国, 张乔根, 邱毓昌, 等. SF6气体放电通道的分形特征及计算机模拟[J].西安交通大学学报, 2000, 34(4): 1-4. Chen Qingguo, Zhang Qiaogen, Qiu Yuchang, et al. Fractal characteristics and computer simulation of the discharge channel in SF6gas[J]. Journal of Xi’an Jiaotong University, 2000, 34(4): 1-4.

[6] 贾志东, 乐波, 蒋雄伟, 等. 分形几何在电介质科学中的应用[J]. 高电压技术, 1999, 25(3): 1-3. Jia Zhidong, Le Bo, Jiang Xiongwei, et al. Fractal geometry and its application in the science of dielectrics[J]. High Voltage Engineering, 1999, 25(3): 1-3.

[7] Cisse H T, Ablart G. The frequency response of a fractal photolithographic structure[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1997, 4(3): 321-326.

[8] Niemeyer L, Pietronero L, Wiesmann H J. Fractal dimension of dielectric breakdown[J]. Physical Review Letters, 1984, 52(12): 1033-1036.

[9] Wiesmann H J, Zeller H R. A fractal model of dielectric breakdown and prebreakdown in solid dielectrics[J]. Journal of Applied Physics, 1986, 60(5): 1770-1773.

[10] Karpov D I, Kupershtokh. A L. Models of streamers growth with "physical" time and fractal characterics of streamer structures[C]//Conference Record of the 1998 IEEE International Symposium on Electrical Insulation, Arlington, VA, 1998: 607-610.

[11] Ding H Z, Varlow B R. Thermodynamic model for electrical tree propagation kinetics in combined electrical and mechanical stresses[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2005, 12(1): 81-89.

[12] 贺恒鑫, 何俊佳, 钱冠军, 等. 棒-板长间隙正极性流注生长概率模型及应用[J]. 高电压技术, 2008, 34(10): 2047-2053. He Hengxin, He Junjia, Qian Guanjun, et al. Stochastic model of streamer growth in air for a rod-plate gap and its application[J]. High Voltage Engineering, 2008, 34(10): 2047-2053.

[13] 谭震宇, 万基磊, 李清泉. 基于分形理论的水中流注放电仿真[J]. 高电压技术, 2012, 38(7): 1556-1561. Tan Zhenyu, Wan Jilei, Li Qingquan. Fractal simulation of streamer discharge in liquid water[J]. High Voltage Engineering, 2012, 38(7): 1556-1561.

[14] 陈伟根, 汪万平, 夏青. 绝缘子污秽放电泄漏电流的多重分形特征研究[J]. 电工技术学报, 2013, 28(1): 50-56. Chen Weigen, Wang Wanping, Xia Qing. Research on multi-fractal characteristics of leakage current for contamination discharge of insulators[J]. Transactions of China Electrotechnical Society, 2013, 28(1): 50-56.

[15] Morrow R, Lowke J J. Streamer propagation in air[J] . Journal of Physics D: Applied Physics, 1997, 30(4): 614-627.

[16] 庄池杰, 曾嵘. 短间隙流注放电数值仿真方法研究进展[J]. 中国电机工程学报, 2012, 32(22): 157-166. Zhuang Chijie, Zeng Rong. Research and development on short gap streamer discharge simulation methods[J]. Proceedings of the CSEE, 2012, 32(22): 157-166.

[17] Georghiou G E, Morrow R, Metaxas A C. A twodimensional, finite-element, flux-corrected transport algorithm for the solution of gas discharge pro-blems[J]. Journal of Physics D: Applied Physics, 2000, 33(19): 605-620.

[18] Lohner R, Morgan K, Peraire J, et al. Finite element flux-corrected transport (FEM-FCT) for the Euler and Navier-Stokes equation[J]. International Journal for Numerical Methods in Fluids, 1987, 10(7): 1093-1109.

[19] Georghiou G E, Morrow R, Metaxasan A C. An improved finite-element flux-corrected transport algorithm[J]. Journal of Computational Physics, 1999, 148(2): 605-620.

[20] 汪沨, 李敏, 李锰, 等. 基于ETG-通量校正传输法的短间隙SF6/N2混合气体流注放电数值仿真[J].电工技术学报, 2016, 31(6): 234-241. Wang Feng, Li Min, Li Meng, et al. Numerical simulation of short gap streamer discharge in SF6/N2gas mixtures based on Euler-Taylor-Galerkin-flux corrected transport method[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 234-241.

[21] Georghiou G E, Morrow R, Metaxas A C. Twodimensional simulation of streamers using the FEFCT algorithm[J]. Journal of Physics D: Applied Physics, 2000, 33(3): 27-32.

[22] Biller P. Fractal streamer models with physical time[C]//Proceedings of IEEE 11th International Conference on Conduction and Breakdown in Dielectric Liquids, Baden-Dattwil, Switzerland, 1993: 199-203.

[23] Noskov M D, Kuktha V R, Lopatin V V. Simulation of the electrical discharge development in inhomogeneous insulators[J]. Journal of Physics D: Applied Physics, 1995, 28(6): 1187-1194.

[24] Pancheshnyi S V, Starikovskaia S M, Yu Starikovskii A. Role of photoionization processes in propagation of cathode-directed streamer[J]. Journal of Physics D: Applied Physics, 2001, 34(1): 105-115.

[25] 孙鹏程, 王帮田, 洪文芳, 等. SF6/N2混合气体绝缘特性的实验研究[J]. 中国电力, 2012, 45(12): 71-75. Sun Pengcheng, Wang Bangtian, Hong Wenfang, et al. Experimental studies on electrical insulation performances of SF6/N2gas mixtures[J]. Electric Power, 2012, 45(12): 71-75.

Simulation of Discharge in SF6/N2Gas Mixtures Based on Fractal Theory

Li Min1,2Wang Feng1Xu Songzhi1Chen Xiaolin1Huang Chizhi1Xie Wangjun1
（1. School of Electrical and Information Engineering Hunan University Changsha 410082 China 2. Changsha Power Supply Company Changsha 410000 China）

In this paper, the model of dielectric breakdown in SF6/N2mixed gas is simulated by using the Matlab programs. This rod-plane model is established considering the distribution of space charge and introducing physical time, based on the fractal theory. The finite element method (FEM) is used to solve the electric field, and particle continuity equations are solved by the flux corrected transport (FCT) algorithm. Moreover, the characteristics of fractal discharge under various scenarios are analyzed, such as different probability exponents, different discharge thresholds, and different percentages of SF6and so on. The simulation results show that the number of branches and fractal dimension decrease with the increasing of probability exponent and the percentage of SF6. The discharge fractal dimensionDof 50%/50% SF6/N2gas mixture equals to 1.219 2, and the average velocity during the discharge process of streamer propagation is 1.15Mm/s. Moreover, the distributions of charge density in space, electric field alone the axis, and electrons density alone the axis are calculated.

Discharge, fractal dimension, SF6/N2mixed gas, finite element method, flux corrected transport, probability exponent

TM213

李 敏 男，1989年生，硕士研究生，研究方向为气体放电仿真。

E-mail: liminzhenqi@163.com（通信作者）

汪 沨 男，1972年生，博士，教授，博士生导师，研究方向为电力设备绝缘技术、气体放电及其应用技术等。

E-mail: Wangfeng55@263.net

教育部新世纪优秀人才支持计划基金（NCET-11-0130）和高等学校博士学科点专项科研基金（20120161110009）资助项目。

2015-10-29 改稿日期 2016-04-03