基于车轨耦合和扣件精细模型的弹条疲劳分析

辛涛，杨学敏，肖宏，张琦



基于车轨耦合和扣件精细模型的弹条疲劳分析

辛涛1, 2, 3，杨学敏1，肖宏1, 2, 3，张琦1

(1. 北京交通大学土木建筑工程学院，北京，100044；2. 轨道工程北京市重点实验室，北京，100044；3. 北京市轨道交通 线路工程与防灾工程技术研究中心，北京，100044)

针对扣件弹条的疲劳断裂问题，利用数值仿真手段对弹条疲劳寿命进行分析。首先，建立车辆−轨道耦合动力分析模型，通过仿真得到轨底垂向位移时程曲线；然后，建立扣件精细分析模型，将轨底垂向位移时程曲线作为输入荷载，计算得到扣件弹条的应力和应变时程曲线；最后，结合疲劳分析方法和累积损伤理论，对弹条的疲劳寿命进行分析。研究结果表明：弹条小圆弧处疲劳寿命最低，最易发生损坏，与现场调查结果一致；弹条疲劳寿命与安装弹程密切相关，随着弹条安装弹程的增大，弹条疲劳寿命急剧降低；为了延长扣件使用寿命，线路运营中应避免弹条的安装弹程过高。

扣件弹条；疲劳寿命；车轨耦合；精细模型；仿真分析

扣件作为轨道结构重要组成部分之一，对城市轨道交通的安全性和舒适性起着重要的影响。随着列车运行密度和速度的提高，扣件在列车循环荷载的作用下容易发生疲劳破坏，导致扣件失效，进而对列车运行安全造成不利影响。近年来，国内外学者针对扣件失效问题进行了针对性研究。对于扣件失效因素，杜茂金[1]对南京地铁用DTⅥ2型扣件进行分析，指出小半径曲线地段钢轨波磨是导致弹条提早失效的主要原因；王文秀等[2]从宏微观角度对SKI15型弹条裂纹及断口进行观察，发现弹条表面存在脱碳层和局部缺陷，容易形成裂纹；郭和平等[3]通过对弹条断口进行化学成分检测，发现弹条表面质量差是弹条断裂的主要原因。在数值仿真方面，朱胜阳等[4]基于有限元理论研究了高铁行车过程中的振动响应，指出钢轨磨耗会加剧弹条振动；肖新标等[5]通过假定失效因子分析了扣件失效程度对行车脱轨的影响；ZHOU等[6]分析了半径7 km曲线段不同扣件失效程度对列车速度的影响；尚红霞等[7]建立扣件系统模型，分析了Ⅲ型弹条不同安装状态对其扣压力和应力的影响。疲劳评价方面，余自若等[8]计算了X2型弹条的应力最大位置，并且估算了疲劳荷载作用下的疲劳寿命；MOHAMMADZADEH等[9−10]通过数值仿真结果和实测数据，分析了不同列车荷载作用下弹条的疲劳可靠度；徐庆元等[11]分析了纵连板式无砟轨道在温度梯度作用下的疲劳应力谱。既有研究大多是从静力角度对弹条的安装状态进行分析，或是将扣件作为影响因素研究其对行车安全的影响，较少见到针对扣件弹条精细模型的动力分析和疲劳寿命估算方面的研究成果。本文作者针对扣件弹条的疲劳问题，选取地铁DTⅥ2型扣件为研究对象，对其疲劳寿命进行估算，以便为延长扣件使用寿命和降低养护维修成本提供参考。

1 计算模型

疲劳破坏是指在连续循环荷载作用下，应力低于极限抗拉强度甚至低于屈服强度时发生的脆性断裂现象[12]。弹条在列车循环荷载作用下发生的破坏属于疲劳破坏。为此，本文建立车辆−轨道耦合动力分析模型和扣件精细分析模型，对扣件弹条在列车荷载下的动力响应进行仿真计算，获得弹条的应力应变时程曲线；然后，对时程曲线进行雨流计数[13]，结合疲劳分析理论分析弹条的疲劳寿命，并探讨不同安装弹程下疲劳寿命的变化规律。分析流程如图1所示。

1.1 车轨耦合分析模型

基于车辆−轨道耦合动力学理论[14]，建立车辆−轨道耦合动力分析模型，获取轨底垂向位移时程曲线。首先，基于多体动力学理论建立车辆模型，基于有限元理论建立轨道模型；然后，通过轮轨接触模型将车辆、轨道耦合起来，形成车辆−轨道耦合动力分析 模型。

车辆模型包括车体、转向架和轮对，如图2所示，在建模过程中将其假定为刚体，彼此之间通过一系、二系弹簧以及阻尼器连接。车体和转向架各有沉浮、点头、横移、侧滚和摇头这5个自由度；每个轮对具有沉浮、横移、侧滚和摇头4个自由度。不考虑车轮转速不均匀产生的回转，总计有31个自由度。

轨道结构建模时，为了获取更加真实的轨底垂向位移时程曲线，轨道采用实体单元建模，还考虑实测轨道不平顺的影响。扣件系统简化为弹簧−阻尼单元，与钢轨及轨道板单元节点连接[15]，轨道模型如图3 所示。

轮轨相互作用时对轮轨法向力和轮轨切向力进行计算，根据Hertz非线性弹性接触理论计算轮轨法向力；车轮与钢轨之间的滑动将产生两者之间的速度差会造成摩擦，车轮与钢轨之间会产生切向力，本文根据罚函数接触算法计算轮轨切向力[16]。

1.2 扣件精细分析模型

为确定弹条受力最不利位置，弹条采用实体单元进行仿真模拟。在车轨耦合模型中，通过计算分别得到轨底和轨道板的动位移。由于轨道板位移较小，轨底动位移与扣件系统的变形量近似相等。扣件系统的变形实际包含弹条、铁垫板和胶垫的位移，在精细化分析模型中，没有对轨道板、胶垫进行建模，计算时保证轨底位移与车轨耦合计算得到的扣件系统变形量一致，这样可实现计算工况的一致性。

首先，建立扣件精细分析模型，并进行装配，如图4所示；然后，对轨底施加强制位移，使扣件达到设定的安装状态；最后，将轨底垂向位移时程曲线作为位移荷载，计算弹条的应力和应变时程曲线。

扣件具有良好的跟随性，可以随着钢轨的振动而振动。弹条与铁垫板、弹条与轨距块之间均存在接触，接触包含法向接触和切向接触。其中，法向接触通过拉格朗日法实施“硬”接触，以此计算法向接触力；切向接触力采用罚函数进行计算。扣件精细分析模型主要分析弹条的应力应变情况，所以，对弹条的网格划分有一定的精度要求。弹条采用六面体单元进行模拟，经过比较单元精度选为2 mm，如图5所示。

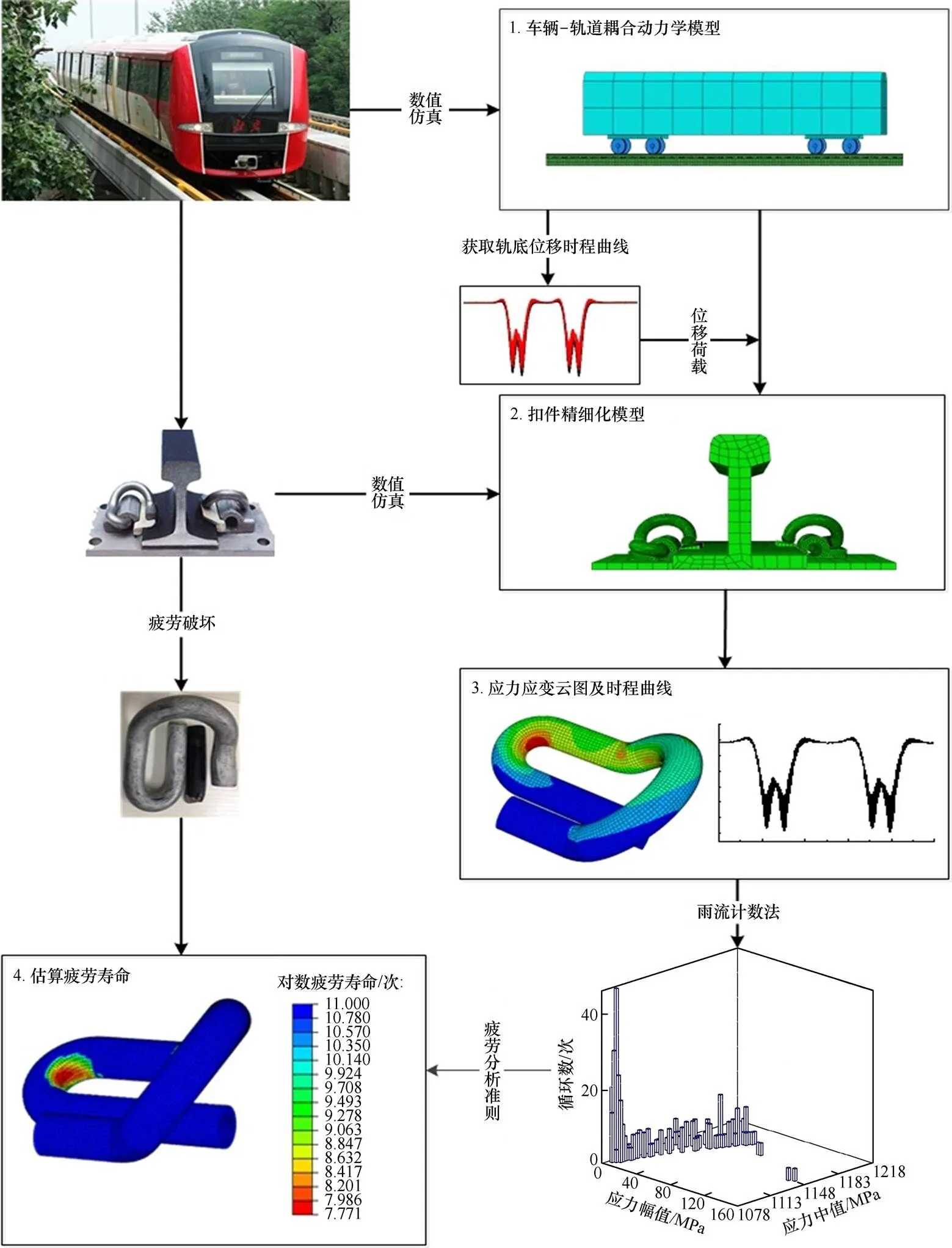
图1 分析流程

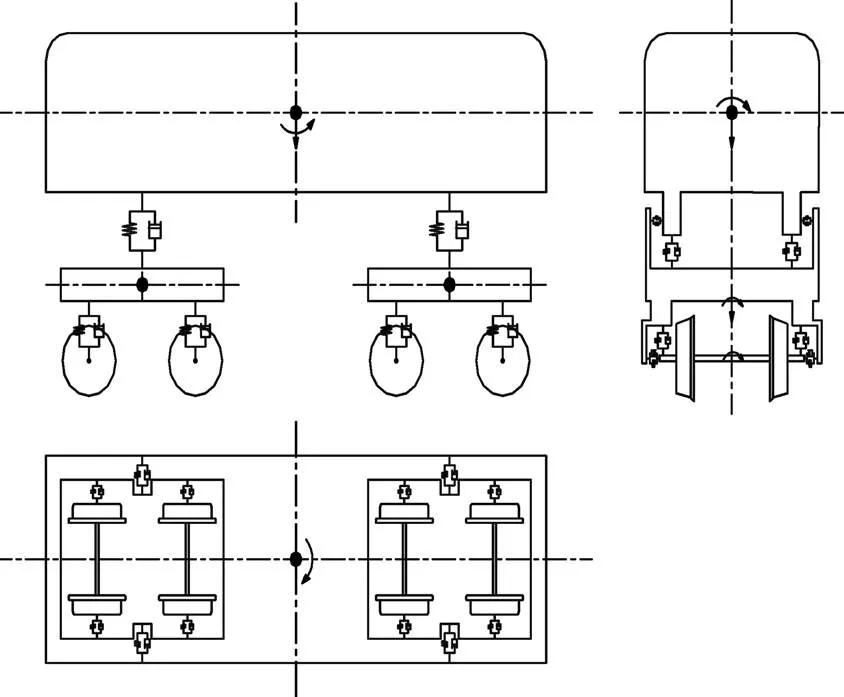
图2 车辆模型示意图

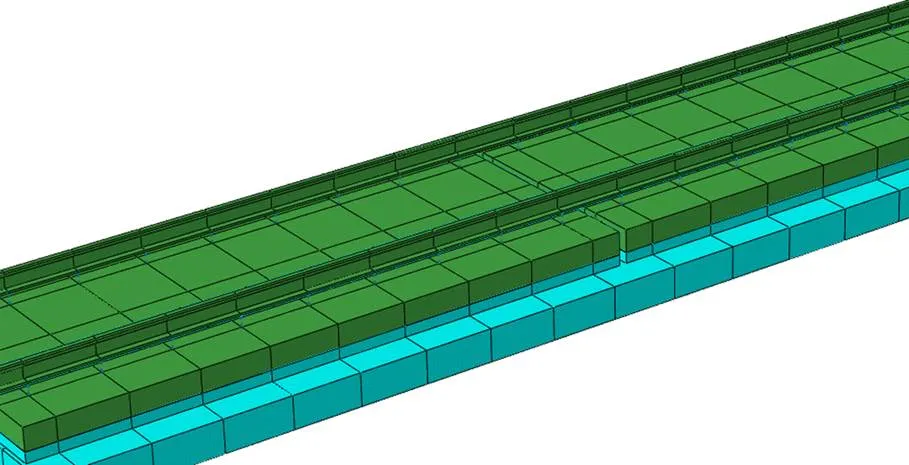
图3 轨道模型

图4 实物安装图与仿真模型

图5 弹条模型

2 计算参数

2.1 车轨耦合模型参数

本文主要模拟列车在直线地段的运行情况，车轨耦合模型按照我国地铁B型车参数进行设置[17]，主要参数如表1所示。

2.2 扣件精细分析参数

根据DTⅥ2型扣件的相关设计图纸，其设计安装弹程为8.0~9.5 mm，主要材料参数如表2所示。

根据文献[18]，弹条由60Si2Mn弹簧钢制成，其屈服强度s=1.480 GPa，抗拉强度b=1.625 GPa。

2.3 疲劳分析参数

采用名义应力法和Brown Miller组合应变法 (简称BM法)，并基于Miner线性累积损伤理论[19]，对弹条进行疲劳寿命分析。其中，名义应力法依据−曲线进行寿命估算，BM法依据−曲线进行寿命估算。

表1 车轨耦合模型主要参数

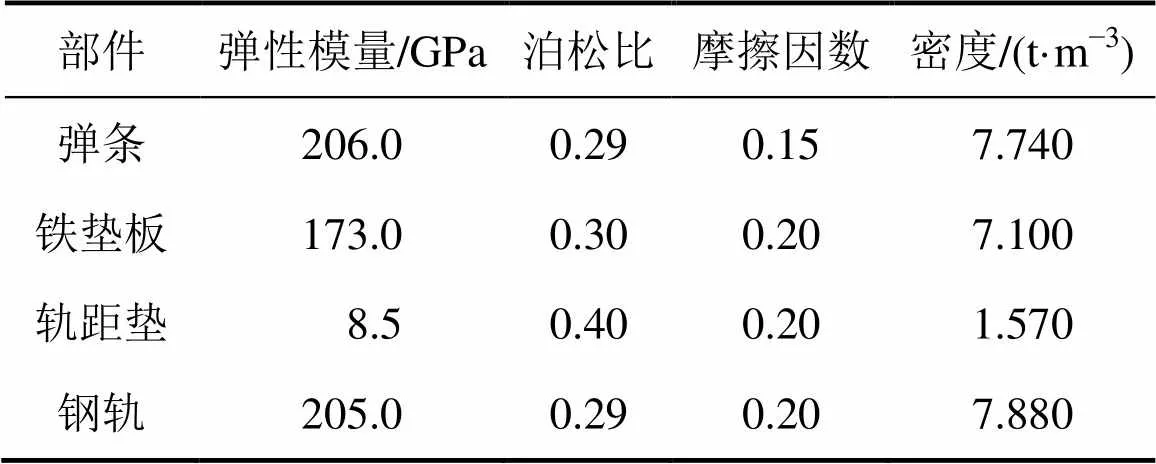
表2 扣件主要参数

2.3.1−曲线的选取

扣件弹条采用60Si2Mn弹簧钢制成，其95%存活率时的−曲线公式为[20]

Seeger算法根据材料弹性模量=205 GPa，泊松比=0.29，抗拉强度b=1. 625 GPa。预测−曲线公式为

式中：为疲劳寿命，次；为应力幅值，MPa；为存活率95%时的对数疲劳寿命；为基于Seeger算法的对数疲劳寿命。根据式(1)和(2)绘制的−曲线如图6所示。

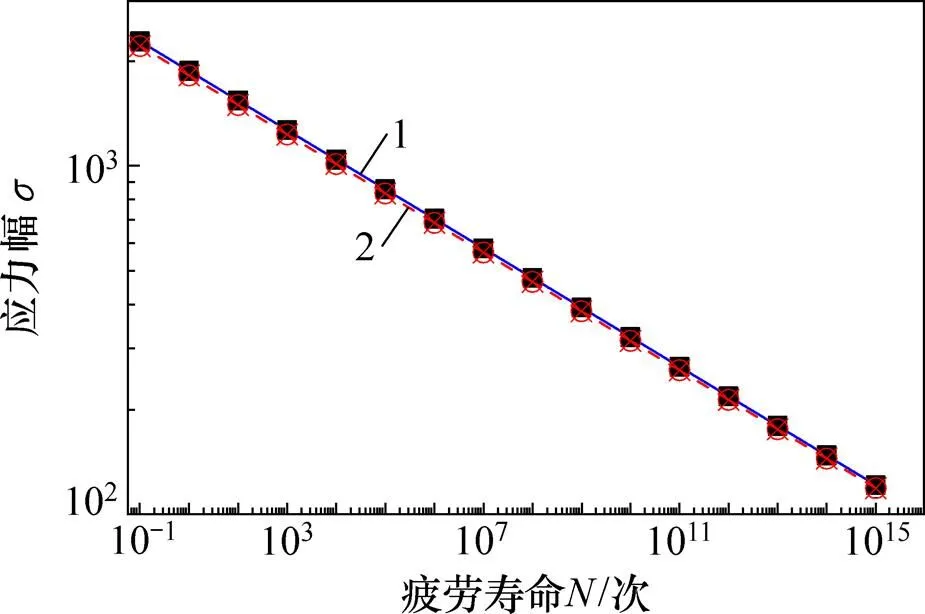
1—Seeger算法；2—95%存活率下的−曲线公式(即式(1))。

图6 不同算法所得的−曲线

Fig. 6−curves obtained by different algorithms

由图6可知：Seeger算法与95%存活率下的−曲线公式(即式(1))所得曲线基本一致，故本文采用95%存活率下的−曲线进行疲劳寿命分析。

2.3.2−曲线的选取

应变疲劳方法又称局部应变法或者局部应力−应变方法，主要用于对承受应力水平较高的构件进行寿命估算。本文根据BM法对弹条的应变−寿命进行分析，其公式如下：

根据通用斜率法得：=−0.12；=−0.6；′=1.75= 2 844 MPa；。式中：0为静拉试验中试件初始横截面积；f为静拉试验中试件断裂时的颈缩面积。本文假设f=0.70，Seeger算法根据材料属性得出的疲劳参数为：=−0.087；=−0.58；；。

根据以上2种算法可得其−曲线如图7所示。

由图7可得：在低周疲劳区，Seeger算法和通用斜率法这2种算法所得曲线基本一致。本文采取Seeger算法得到的−曲线进行寿命估算。

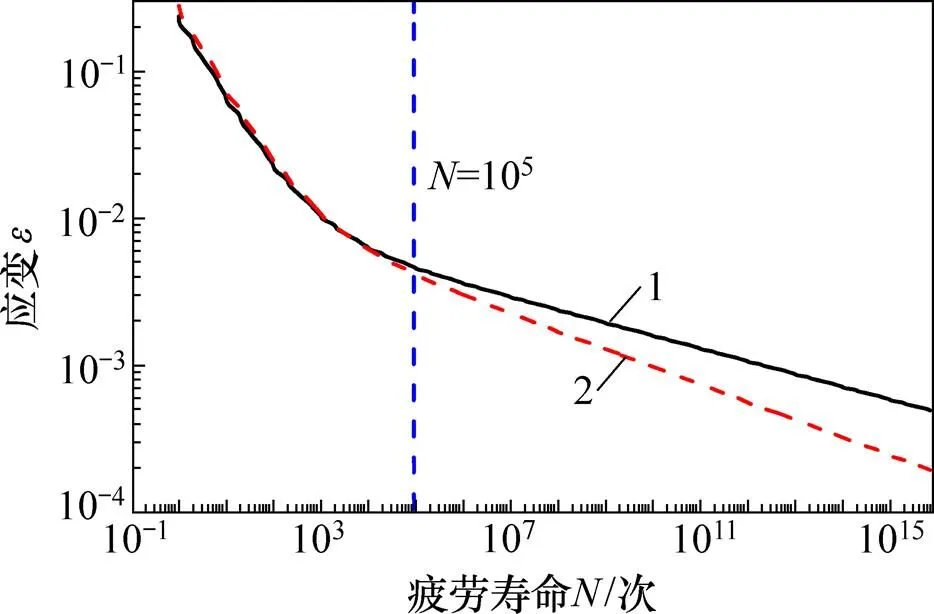
1—Seeger算法；2—通用斜率法。

图7 不同算法所得的−曲线

Fig. 7−curves obtained by different algorithms

3 计算结果

3.1 轨底垂向位移时程曲线的获取

通过车轨耦合模型，获得列车在直线段以100 km/h的速度运行时的轨底垂向位移时程曲线，如图8所示。

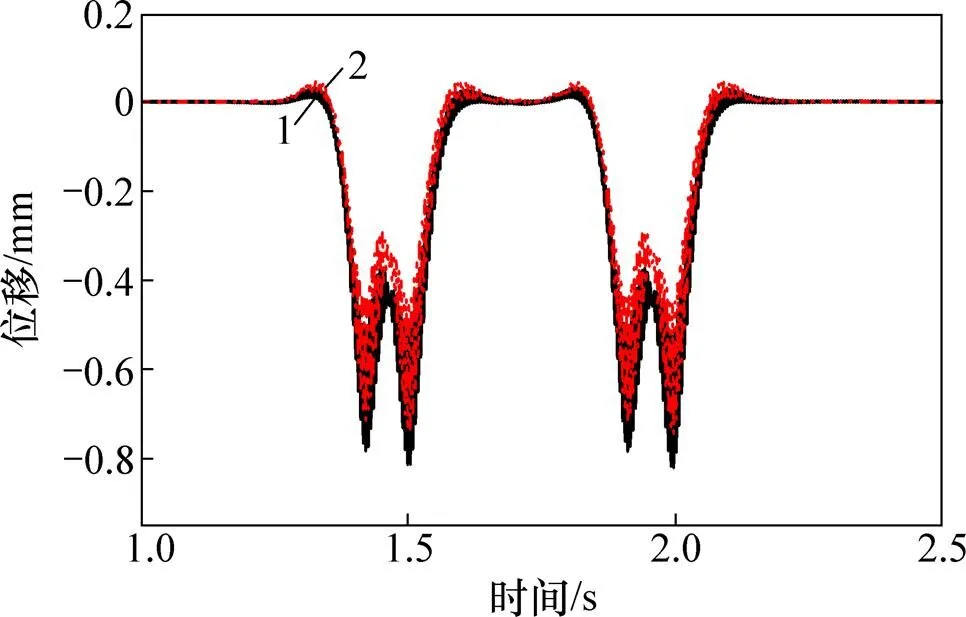
1—内侧位移；2—外侧位移。

图8 轨底垂向位移时程曲线

Fig. 8 Time history curves of rail foot vertical displacement

由图8可知：内侧轨底垂向位移最大值为0.82 mm，外侧轨底垂向位移最大值为0.75 mm，内侧较外侧位移大9.3%。考虑最不利荷载情况，本文采用位移较大的内侧垂向位移时程曲线作为激励。

3.2 弹条受力分析

线路正常运营中，扣件通过与轨距垫紧密接触来提供扣压力，不同安装弹程下的受力情况不同。安装弹程为8 mm时的应力云图如图9所示。

由图9可得：弹条最大应力为1.286 GPa，发生于弹条小圆弧处；沿着小圆弧到大圆弧的路径，其应力逐渐降低；弹条中肢和趾端应力较小。

当列车通过时，应力、应变均随着时间急剧变化，应力最大节点处的应力时程曲线如图10所示，应变时程曲线与此类似。

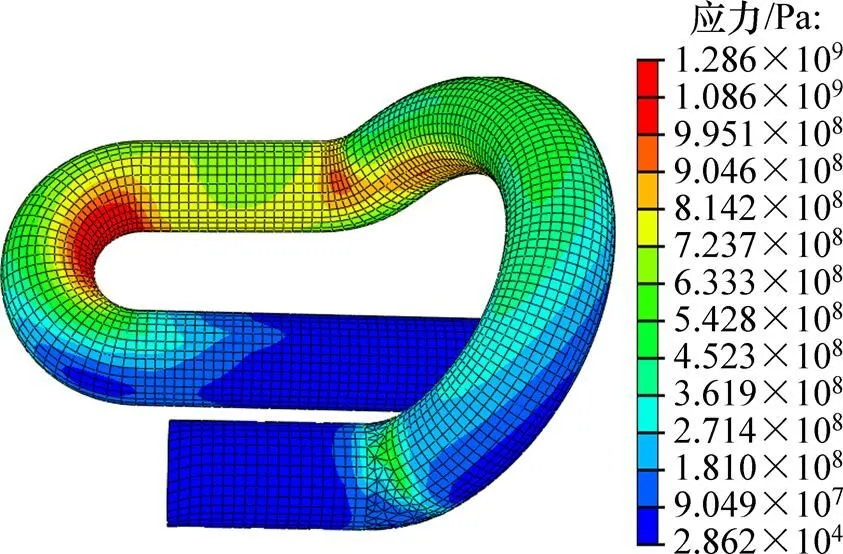
图9 应力云图

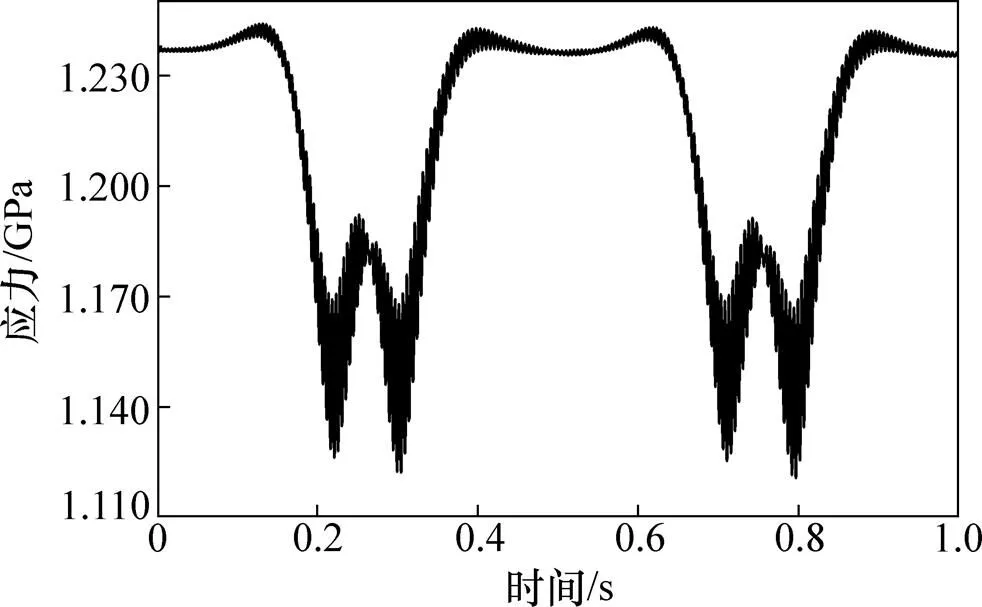
图10 应力时程曲线

3.3 疲劳寿命分析

除了列车荷载引起的动应力外，扣件应力状态与安装弹程密切相关，本文重点研究安装弹程变化对弹条疲劳寿命的影响。安装弹程为8 mm时的疲劳寿命云图如图11所示。

由图11可得：弹条的疲劳破坏位置处于弹条小圆弧处，与现场统计的断裂频发位置相符合；不同安装弹程下的寿命云图与图11类似，疲劳寿命最不利位置均处于弹条小圆弧处。本文研究不同安装弹程时弹条疲劳寿命的变化规律，基于名义应力法和BM法计算得到的疲劳寿命结果如图12所示。

由图12可得：随着安装弹程增大，其疲劳寿命逐渐下降，且其下降趋势越来越大。整体来看，当安装弹程在7.0~10.0 mm之间时，采用BM法较名义应力法估算得到的疲劳寿命更低，BM法计算结果更保守；当安装弹程达到10.0 mm以后，这2种算法计算所得疲劳寿命基本相同。

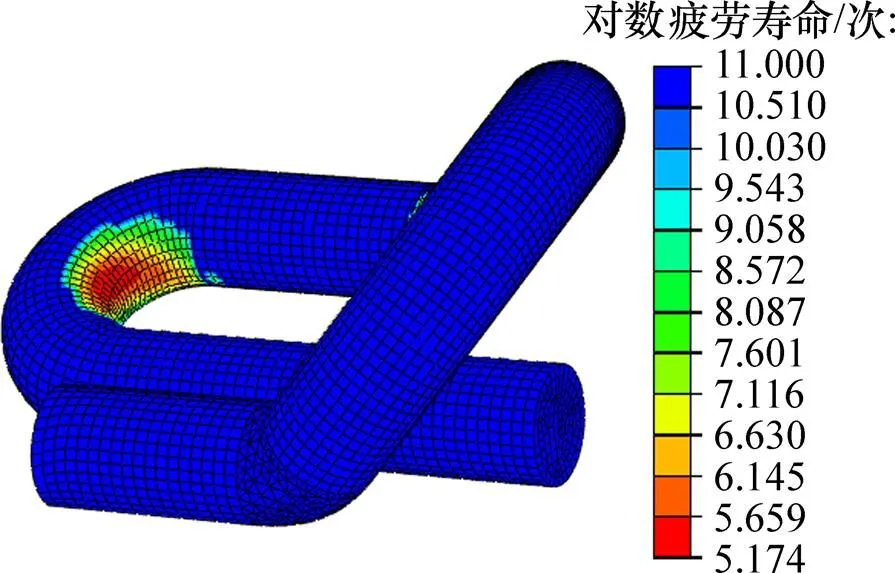
图11 疲劳寿命云图

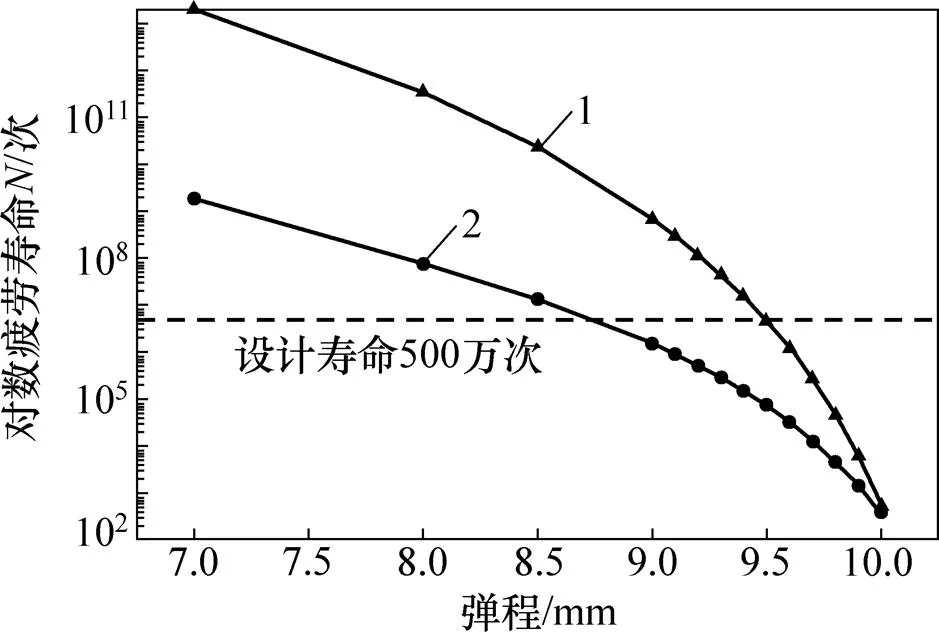
1—应力−寿命(名义应力法)；2—应变−寿命(BM法)。

图12 不同安装弹程下的疲劳寿命

Fig. 12 Fatigue life under different installation heights

假定弹条的疲劳寿命期望不低于500万次，为了满足疲劳寿命要求，若采用名义应力法，则安装弹程应该不高于9.5 mm；若采用BM法，则安装弹程应该不高于8.8 mm。

在现场运营中，提高扣件的安装弹程可以增大扣压力，这是保持扣件阻力的重要措施。本文计算结果表明：扣件安装弹程过大，会导致弹条疲劳寿命显著降低。因此，从延长扣件使用寿命角度，建议合理控制扣件的安装弹程。在本文所选计算条件下，DTⅥ2型扣件的合理安装弹程为7~9 mm，这样既可以满足扣压力的要求，又能保证扣件具有较长使用寿命。

4 结论

1) 弹条小圆弧处应力、应变最大，疲劳寿命最低，是疲劳破坏易发区，与实际弹条断裂位置相同。

2) 安装弹程对弹条的疲劳寿命影响显著。随着安装弹程的增加，疲劳寿命随之下降，且下降趋势逐渐增大。

3) 安装弹程过低会导致扣压力不足，而过高则会明显降低扣件使用寿命。在本文计算条件下， DTVI2型扣件的安装弹程建议控制在7~9 mm之间。

[1] 杜茂金. 南京地铁DTⅥ2型扣件弹条折断原因分析[J]. 城市轨道交通, 2009, 12(7): 40−42. DU Maojin. Analysis of DTVI2 type fastener broken shells in Nanjing metro[J]. Urban Mass Transit, 2009, 12(7): 40−42.

[2] 王文秀, 王振, 赵磊, 等. 高速铁路用SKl15型弹条失效分析[J]. 金属热处理, 2013, 38(12): 108−112. WANG Wenxiu, WANG Zhen, ZHAO Lei, et al. Failure analysis of SKI15 spring fasteners for high-speed railway[J]. Heat Treatment of Metals, 2013, 38(12): 108−112.

[3] 郭和平, 李彪, 李玉生. 60Si2MnA弹条断裂分析[J]. 失效分析与预防, 2011, 6(2): 90−95. GUO Heping, LI Biao, LI Yusheng. Fracture analysis of 60Si2MnA spring rod[J]. Failure Analysis and Prevention, 2011, 6(2): 90−95.

[4] 朱胜阳, 蔡成标, 尹镪, 等. 高速铁路扣件弹条动力学分析[J]. 工程力学, 2013, 30(6): 254−258. ZHU Shenyang, CAI Chengbiao, YIN Qiang, et al. Dynamic analysis of rail fastening clip in high-speed railway[J]. Engineering Mechanics, 2013, 30(6): 254−258.

[5] 肖新标, 金学松, 温泽峰. 钢轨扣件失效对列车动态脱轨的影响[J]. 交通运输工程学报, 2006, 6(1): 10−15. XIAO Xinbiao, JIN Xuesong, WEN Zefeng. Influence of rail fastener failure on vehicle dynamic derailment[J]. Journal of Traffic and Transportation Engineering, 2006, 6(1): 10−15.

[6] ZHOU Li, SHEN Zhiyun. Dynamic analysis of a high-speed train operating on a curved track with failed fasteners[J]. Journal of Zhejiang University Science A, 2013, 14(6): 447−458.

[7] 尚红霞, 温泽峰, 吴磊, 等. 地铁扣件Ⅲ型弹条失效有限元分析[J]. 工程力学, 2015, 32(9): 210−215. SHANG Hongxia, WEN Zefeng, WU Lei, et al. Finite element analysis of type III rail fastening clip failure in metro lines[J]. Engineering Mechanics, 2015, 32(9): 210−215.

[8] 余自若, 袁媛, 张远庆, 等. 高速铁路扣件系统弹条疲劳性能研究[J]. 铁道学报, 2014, 36(7): 90−95. YU Ziruo, YUAN Yuan, ZHANG Yuanqing, et al. Fatigue properties of elastic bars of fastening systems installed with high-speed railways[J]. Journal of the China Railway Society, 2014, 36(7): 90−95.

[9] MOHAMMADZADEH S, AHADI S, NOURI M. Stress-based fatigue reliability analysis of the rail fastening spring clip under traffic loads[J]. Latin American Journal of Solids and Structures, 2014, 11(6): 993−1011.

[10] MOHAMMADZADEH S, AHADI S, KESHAVARZIAN H. Assessment of fracture reliability analysis of crack growth in spring clip type Vossloh SKL14[J]. Proceedings of the Institution of Mechanical Engineers. Part O: Journal of Risk and Reliability, 2014, 228(5): 461−468.

[11] 徐庆元, 孟亚军, 李斌, 等. 温度梯度作用下纵连板式无砟轨道疲劳应力谱[J]. 中南大学学报(自然科学版), 2015, 46(2): 737−741.XU Qingyuan, MENG Yajun, LI Bin, et al. Fatigue stress spectrum of longitudinally connected ballastless track under temperature gradient[J]. Journal of Central South University (Science and Technology), 2015, 46(2): 737−741.

[12] 姚卫星. 结构疲劳寿命分析[M]. 北京: 国防工业出版社, 2004: 25−78. YAO Weixing. Fatigue life prediction of structures[M]. Beijing: National Defense Industry Press, 2004: 25−78.

[13] 王宏伟, 邢波, 骆红云. 雨流计数法及其在疲劳寿命估算中的应用[J]. 矿山机械, 2006, 34(3): 95−97.WANG Hongwei, XING Bo, LUO Hongyun. Rain-flow count method and application on fatigue life estimation[J]. Mining & Processing Equipment, 2006, 34(3): 95−97.

[14] 翟婉明. 车辆−轨道耦合动力学[M]. 3版. 北京: 中国铁道出版社, 2007: 12−78. ZHAI Wanming. Vehicle−track coupling dynamics[M]. 3rd ed. Beijing: China Railway Press, 2007: 12−78.

[15] 徐庆元, 李斌, 周小林. 高速列车作用下路基上板式无砟轨道动力系数[J]. 中南大学学报(自然科学版), 2011, 42(9): 2831−2836. XU Qingyuan, LI Bin, ZHOU Xiaolin. Dynamic coefficient of slab track system on subgrade under high-speed trains[J]. Journal of Central South University(Science and Technology), 2011, 42(9): 2831−2836.

[16] 常崇义. 有限元轮轨滚动接触理论及其应用研究[D]. 北京: 中国铁道科学研究院, 2010: 19−42. CHANG Chongyi. A study on wheel/rail rolling contact theory based on finite element method and its applying[D]. Beijing: China Academy of Railway Sciences, 2010: 19−42.

[17] 魏一夫. 地铁列车荷载作用下单元板式无砟轨道和隧道的动力分析[D]. 长沙: 中南大学土木工程学院, 2013: 28−30. WEI Yifu. Dynamic analysis of unit plate track and tunnel under train loading[D]. Changsha: Central South University. College of Civil Engineering, 2013: 28−30.

[18] 程尔泽. 60Si2Mn弹簧钢热处理工艺与性能的关系[J]. 理化检验(物理分册), 1997, 33(3): 24−30. CHENG Erze. The relationship between heat treatment technology and property of 60Si2Mn spring steel[J]. Physical Testing and Chemical Analysis (Physical Testing), 1997, 33(3): 24−30.

[19] 杨晓华, 姚卫星, 段成美. 确定性疲劳累积损伤理论进展[J]. 中国工程科学, 2003, 5(4): 80−87. YANG Xiaohua, YAO Weixing, DUAN Chengmei. The review of ascertainable fatigue cumulative damage rule[J]. Engineering Sciences, 2003, 5(4): 80−87.

[20] 赵永翔, 杨冰, 彭佳纯. 寿命服从对数正态分布、有置信度时概率疲劳曲线的合理重构[J]. 应用数学和力学, 2007, 28(4): 413−418. ZHAO Yongxiang, YANG Bing, PENG Jiachun. Rebuilding of the probabilistic S-N curves under fatigue life following lognormal distribution with a given confidence[J]. Applied Mathematics and Mechanics, 2007, 28(4): 413−418.

(编辑 陈灿华)

Fatigue analysis of spring clip based on vehicle-track coupled model and detailed fastener model

XIN Tao1, 2, 3, YANG Xuemin1, XIAO Hong1, 2, 3, ZHANG Qi1

(1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;2. Beijing Key Laboratory of Track Engineering, Beijing 100044, China;3. Beijing Engineering Research Center of Rail Traffic Line Safety and Disaster Prevention, Beijing 100044, China)

Aiming at the fatigue fracture problem of rail fastening spring clip, a numerical simulation method was used to estimate its fatigue life. Firstly, a vehicle-track coupled model was established and the time history curve of rail foot vertical displacement was obtained. Secondly, a detailed fastener model was established, which uses the rail foot displacement curve as input loads. Then, the time history curves of spring clip stress and strain were obtained. Finally, the fatigue life of spring clip was analyzed according to the fatigue analysis method and cumulative damage theory. The results show that the small curve area of spring clip has the lowest fatigue life and is the most prone to damage, which is consistent with the field survey results. In addition, the fatigue life is closely related to the installation height. With the increase of the installation height, the life is sharply reduced. In order to extend the fastener service life, the excessive installation of the spring clip during operation should be avoided.

rail fastening spring clip; fatigue life; vehicle-track coupling; detailed model; simulation analysis

10.11817/j.issn.1672-7207.2016.12.040

U213.5+31

A

1672−7207(2016)12−4270−07

2016−02−20；

2016−04−18

国家自然科学基金资助项目(51208034，51578055)；中央高校基本科研业务费专项资金资助项目(2015JBZ012)；中国铁路总公司科技研究开发计划项目(2015G001)(Projects(51208034, 51578055) supported by the National Natural Science Foundation of China; Project(2015JBZ012) supported by the Fundamental Research Funds for the Central Universities; Project(2015G001) supported by the Research & Development Program of China Railway Corporation)

辛涛，博士，讲师，从事轨道动力学研究；E-mail: xint@bjtu.edu.cn