通道高度对竖通道内旋转火焰热流场的影响

霍岩，黄德香，邹高万，李树声



通道高度对竖通道内旋转火焰热流场的影响

霍岩，黄德香，邹高万，李树声

(哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨，150001)

以一底面边长0.32 m的方形竖通道为研究对象，利用数值方法对通道高度为0.8~2.0 m的旋转火焰热流场进行模拟。研究通道高度对温度、切向旋转速度、竖直向上运动速度的影响。研究结果表明：通道高度增加会加强通道内火焰的旋转，增加由通道侧开缝引射空气进入通道的能力。然而，通道高度对旋转较为剧烈区域顶端和可见火焰顶端的螺旋线角度影响较小，两者角度平均值分别为44.7°和60.9°。

旋转火焰；通道高度；热流场

城市建筑火灾中，火焰在有侧开缝的竖通道型结构空间内容易发生旋转，从而表现出更快的燃烧速度和更高的火焰高度，会加剧火灾的破坏力，并加大火灾的扑救难度[1]。此类受限空间内的旋转火焰(internal fire whirls)特性受通道结构边界等条件的影响较大。以往人们对旋转火焰的研究多是在固定高度通道内进行，竖通道与边界开口等仅作为形成切向流速从而引发火焰旋转的必要条件。例如CHOW等[1−2]在底面边长0.35 m，高度1.45 m(通道高度与底面边长之比约为4.2)的竖通道内进行了旋转火焰实验研究；LEI等[3−4]均在底面边长2 m，高度15 m(通道高度与底面边长之比为7.5)的竖通道内进行了旋转火焰实验和数值模拟研究；HUO等[5−7]在底面边长2.1 m，高度9 m(通道高度与底面边长之比约为4.3)的竖通道内进行了实验和数值模拟研究；霍岩等[8−9]在底面边长0.32 m，高度2 m(通道高度与底面边长之比约为6.25)的竖通道内进行了实验和数值模拟研究；CHUAH等[10]在1.2 m高的竖通道内进行了倾斜状态下的旋转火焰实验研究。然而在可形成旋转火焰的竖通道内，由于通道高度的不同而对其内部旋转火焰热流场所带来的影响却鲜有研究。鉴于通道高度也可能是影响其内旋转热流场的重要因素之一，本文作者以一竖通道内旋转火焰实验为基础，利用数值模拟方法对改变竖通道高度后的流场变化进行了比较分析。

1 模拟条件与数学物理模型

文献[8]中曾在两侧壁面斜对侧开缝的竖通道内进行旋转火焰实验和数值模拟，结果表明可形成较强烈的旋转火焰。参考其实验通道尺寸和结构以及可形成较强烈的旋转火焰时的开口条件，以底面边长×边长为0.32 m×0.32 m的竖通道为研究对象，通道顶部开口开放，通道两侧壁面各有宽度为0.035 m的斜对开缝。竖通道底面中心放置直径为0.1 m的圆形液体正庚烷燃料池。有侧开缝的竖通道模型示意图如图1所示。

竖通道四周侧壁面沿高度方向的最大值，即通道的整体高度分别为0.8，1.0，1.2，1.4，1.6，1.8和2.0 m，通道高度与底面边长之比*分别为2.500，3.125，3.750，4.375，5.000，5.625，6.250。由于侧开缝是由通道最底端延伸至最顶端，所以在通道高度改变的同时，通道两侧壁面上的侧开缝长度也随之改变。

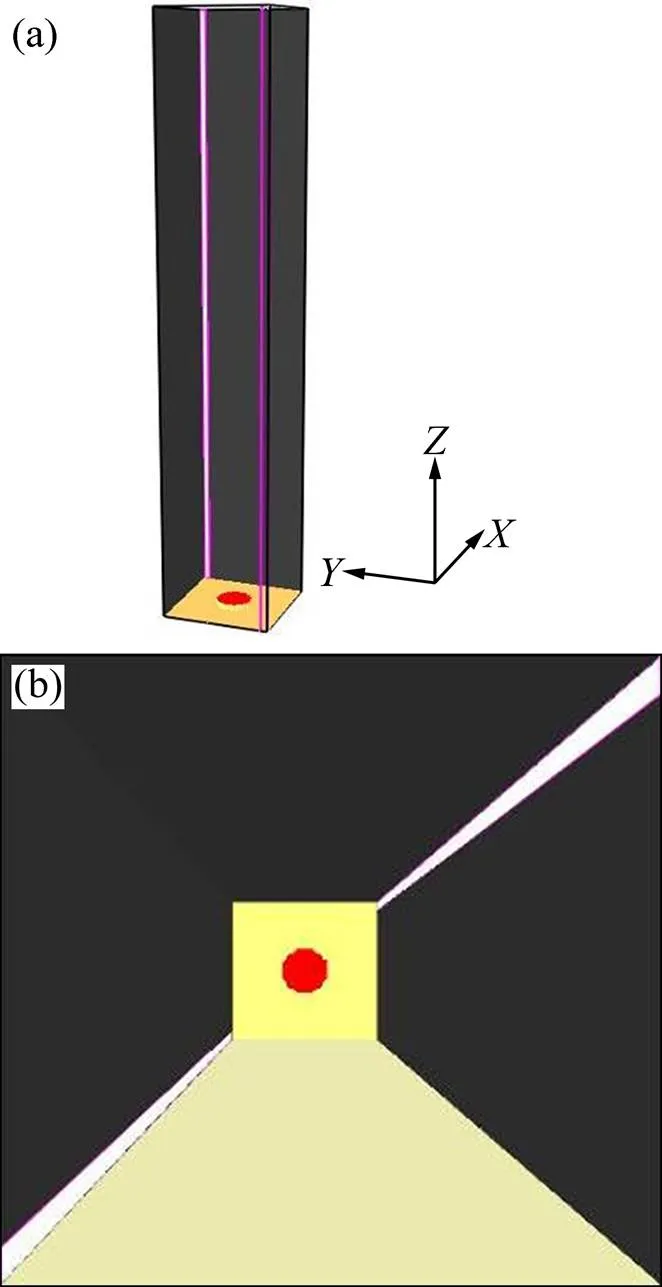
(a) 侧视图；(b) 俯视图

图1 竖通道模型示意图

Fig. 1 Schematic diagram of vertical shaft model

由通道侧开缝引射空气所形成的非受迫旋转火焰流场基本动力学方程组、为加快计算速度和结果收敛所进行的公式简化等见文献[8]。

数值计算时将液体燃料的燃烧简化为单步不可逆反应，采用混合分数燃烧模型，可燃物燃烧消耗单位质量氧气所释放的能量取1.31 kJ/g[11]。决定液体燃料燃烧速度的燃料池表面蒸汽压力cc由Clausius− Clapeyron公式[12]来限制：

式中：为气体常数；cc为液体燃料表面温度；为液体燃料的汽化热，对于实验所使用的正庚烷燃料，取值为480 J/g；boil为燃料沸点温度，取值为98.4 ℃；0为大气压力，取值为101.325kPa。燃料属性参照实验用正庚烷燃料属性[13]，流场中的辐射热传递采用有限体积法来求解。边界层速度与黏性应力基于Werne与Wengle边界层模型[14]来计算。具体设置见文献[8]。

在采用大涡模拟对通道内流场进行计算时，为了精确地捕捉到细节特征，要求特征直径*至少能覆盖10个网格[15]。特征直径*的表达式为

数值计算过程使用美国国家标准与技术研究院(NIST)开发的数值模拟软件FDS(fire dynamics simulator)来实现，该软件对于竖通道内旋转火焰热流场模拟的有效性已在文献[8]中利用Euclidean函数分析法[16]得到了验证。

2 结果与分析

不同高度通道内，液体燃料燃烧稳定时所形成的热释放速率如图2所示。随着通道高度增加，火源热释放率略有上升，变化斜率为0.293，说明通道高度增加后会对火源燃烧起到一定程度的增强作用。

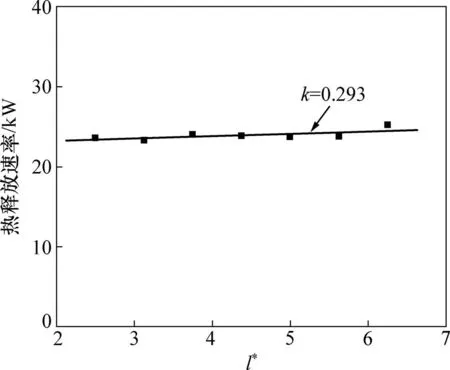
图2 不同高度通道内的热释放率

不同高度通道内，稳定时中轴线上最高温度所在高度和通道整体高度之比H*、竖直向上运动的最大轴向速度所在高度与通道整体高度之比H*如图3所示。由图3可以看出：随着通道高度增加，H*近似线性下降，下降曲线斜率接近通道高度增加的变化率，这说明通道高度增加后，温度最高值所在的高度近似保持不变。同时，随着通道高度增加，H*整体趋势虽略有小幅度下降，但基本维持在0.5附近，说明尽管通道高度不同，但竖直方向向上运动的流速最大值所在高度基本都保持在通道中部附近区域。

图4所示为随着*的变化，通道内热流场稳定时中轴线气流上升速度最大值c-max分布。由图4可知：随着*的增大，c-max近似线性增大，斜率为0.63，说明竖通道内向上的抽拉作用随着通道高度增加而增强，并且促进通道内热气流竖直向上运动的速度加快的作用也更明显。

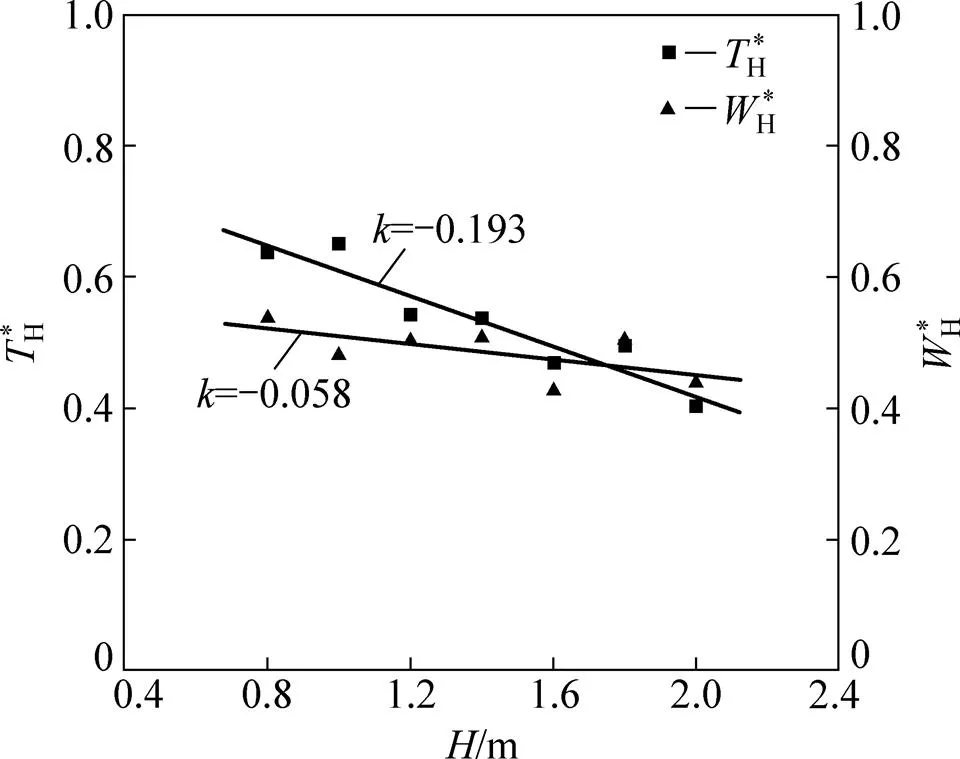
图3 通道内最高温度位置与通道高度之比

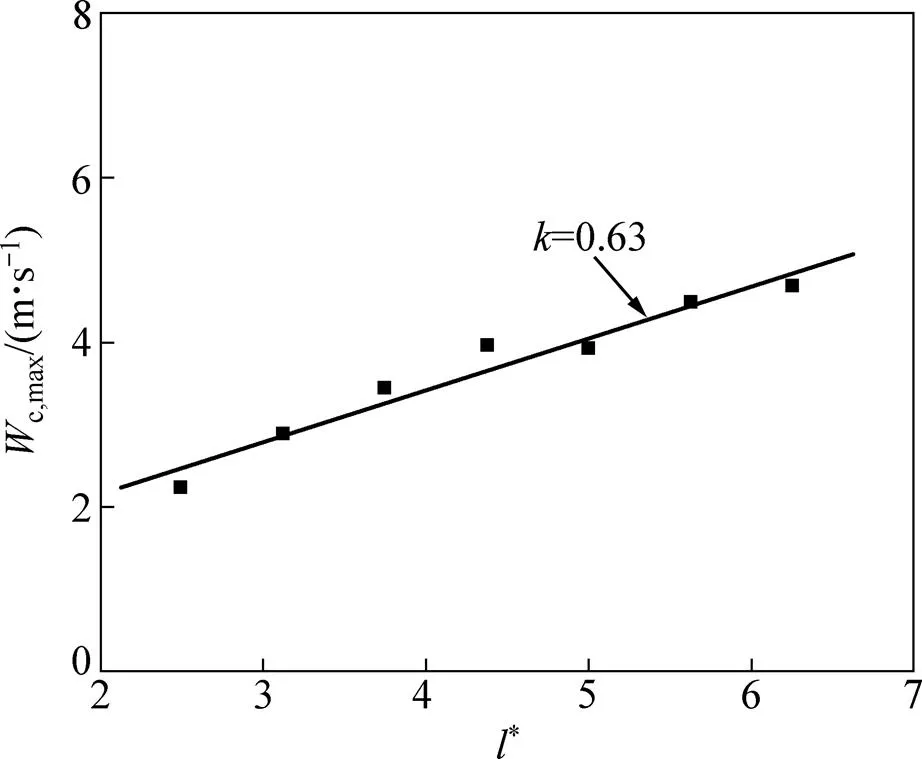
图4 不同高度的通道内中轴线气流上升速度最大值

图5所示为通道内流场稳定时，距燃料池圆心0.05 m旋转气流的切向速度沿高度的变化曲线。由图5可以看出：在竖通道下部空间较大而在上部空间较小，而且随着高度增大，先以很小幅度的增高，之后达到最大值附近比较平缓的阶段，最后逐渐减小即旋转程度逐渐减弱。不同竖通道高度最顶端区域的气流切向速度均降至0.2~0.3 m/s。

图6所示为不同高度通道内距燃料池圆心0.05 m处气流上升速度最大值up,max和切向速度最大值max的分布。由图6可知：随着*增大，up,max和max均近似线性增大，说明通道高度增加也使通道内流场的旋转加剧。up,max的上升斜率明显大于max的上升斜率，说明竖通道高度增加后，使通道内空气所受浮升力与剪切力均有所增大，浮升力增大的幅度约为横向剪切力增大幅度的1.5倍。

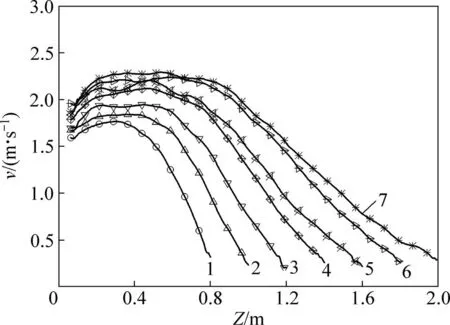
/m：1—0.8；2—1.0；3—1.2；4—1.4；5—1.6；6—1.8；7—2.0。

图5 切向速度沿高度变化

Fig. 5 Tangential velocity variation along height

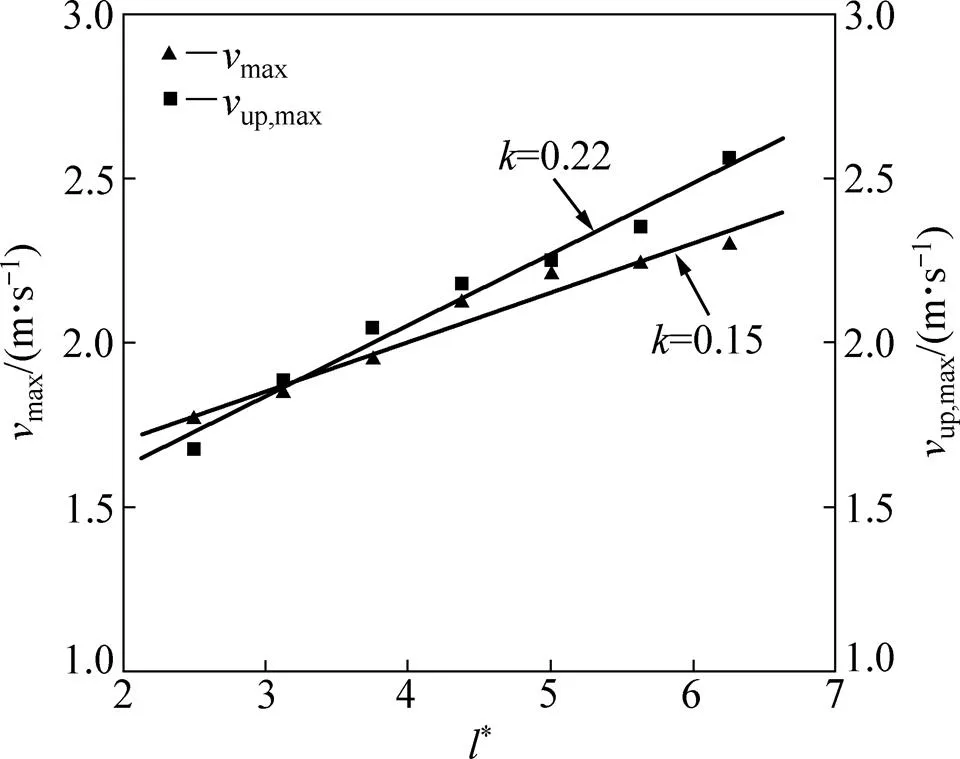
图6 不同高度通道内切向速度和气流上升速度最大值

不同通道高度时，距燃料池圆心0.05 m处最大切向速度所在高度和通道整体高度的比值H*如图7所示。由图7可以看出：随着通道高度增加，比值H*呈缓慢下降趋势，在研究的通道高度范围内，比值H*由0.38降至0.25，最大切向速度所在位置由通道的下部1/3高度附近区域降至通道1/4高度附近。说明通道高度增加后，最大切向速度的所在高度虽有所升高，但其升高的幅度相对于通道高度增加的幅度小。

图8所示为通道侧开缝不同高度处引射进通道内的气体流速的变化曲线。由图8可以看出：流速的变化曲线与图5作用于火焰边沿附近的切向速度变化曲线规律相似，均为在竖通道下部较大而在上部附近迅速降低，这说明在竖通道外部流入的空气主要由侧开缝下部进入，在接近通道顶部附近区域流速可为负值，表明在此处有气流由通道内经侧开缝流出通道。对于不同的通道高度，由侧开缝流入通道的流速随着通道高度的增大而逐渐增加，说明通道高度越高由侧开缝向通道内引射空气的能力越强。

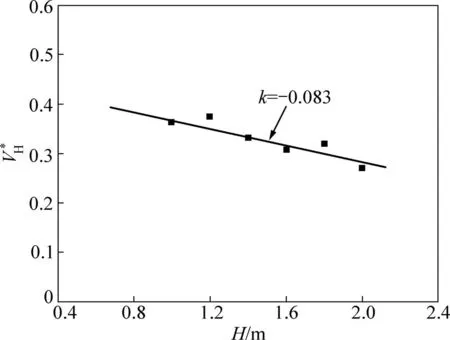
图7 最大切向速度所在高度和通道高度之比

图9所示为由竖通道侧开缝引射进入通道内部的流速最大值max随着竖通道高度的变化。从图9可以看出：随着通道高度的增大，max以斜率为0.06近似线性增大。说明通道高度增加会加强对通道外部空气的引射能力，使流经侧开缝的引射流速度增大，但其增大的幅度要小于通道高度增加的幅度。

/m：1—0.8；2—1.0；3—1.2；4—1.4；5—1.6；6—1.8；7—2.0。

图8 通道侧开缝处气体流速沿高度变化

Fig. 8 Velocity of gas at shaft gap along height

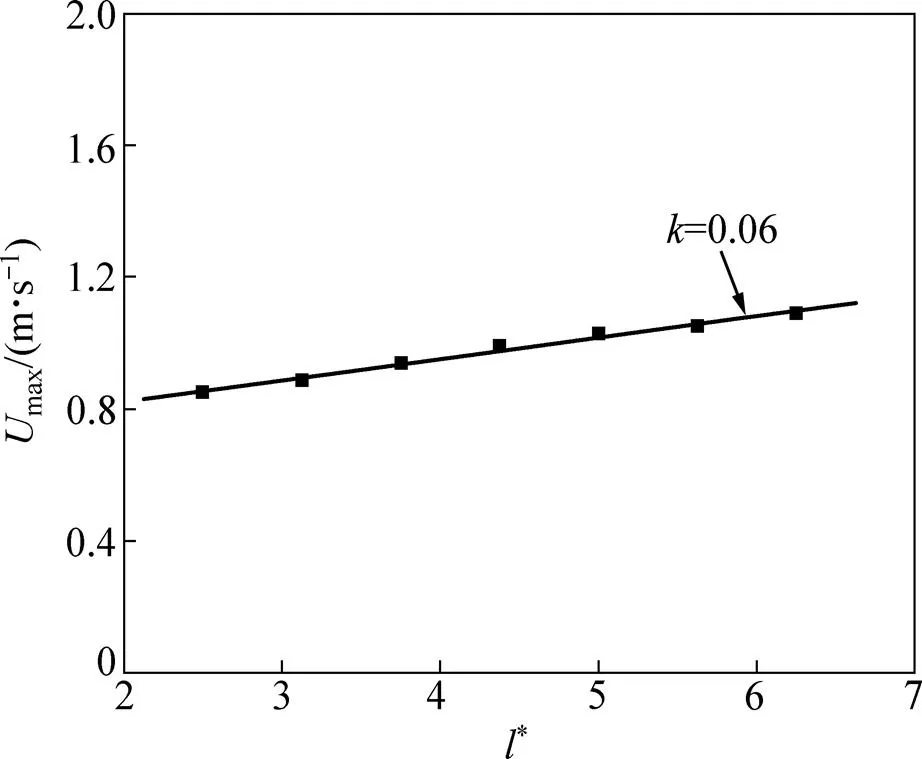
图9 不同高度竖通道侧开缝处最大引射速度

对于气流切向速度和上升速度up，若令，则通道高度为1.0~2.0 m时，和沿高度的变化曲线如图10所示。由图10可以看出：各通道高度时的和变化曲线都是先上升，经历一个波峰后下降；曲线的波峰所在高度位置较曲线的低，说明通道由下至上切向速度先达到最大值随后达到竖直运动的速度最大值。和相比，的波峰比较陡峭，而的波峰更平缓，说明切向速度在较大值附近持续的高度范围较大。由图10还可以看出：尽管通道高度不同，但均满足曲线波峰结束的位置与变化曲线波峰开始的位置大致相同，即通道内高度升高到旋转速度开始降低后随即火焰浮升速度增大到最大值稳定段，这间接反映出流场在竖向高度上旋转切向力为主导运动的区域和浮力为主导的竖直向上运动区域的分区特性。

竖通道内旋转热流场中，火焰高温产生的浮力和旋转切向力是流场的主要受力，若将火焰外边沿区域的气流速度简化为浮力导致的竖向速度up和旋转切向力导致的切向速度的两者合成，则流场螺旋线角度即可简化为气流速度方向与水平面之间的夹角。根据反正切公式可求得螺旋线角度：

图12所示为不同高度竖通道中的螺旋线角度随着高度的变化曲线。由图12可知：在竖通道底部附近，旋转较剧烈，螺旋线角度比较小，均约为20°；随着的增大快速增大，在通道上半部分可达60°以上。流场的螺旋线角度越小，说明流场中浮升力相对于横向剪切力越小，反之，则说明流场中浮力的作用强于剪切力。同时，在相同高度上，通道整体高度越高则螺旋线夹角越小，尤其是高度大于0.4 m时更为明显，这说明通道高度增加后，使相同位置处流场的螺旋程度加强。

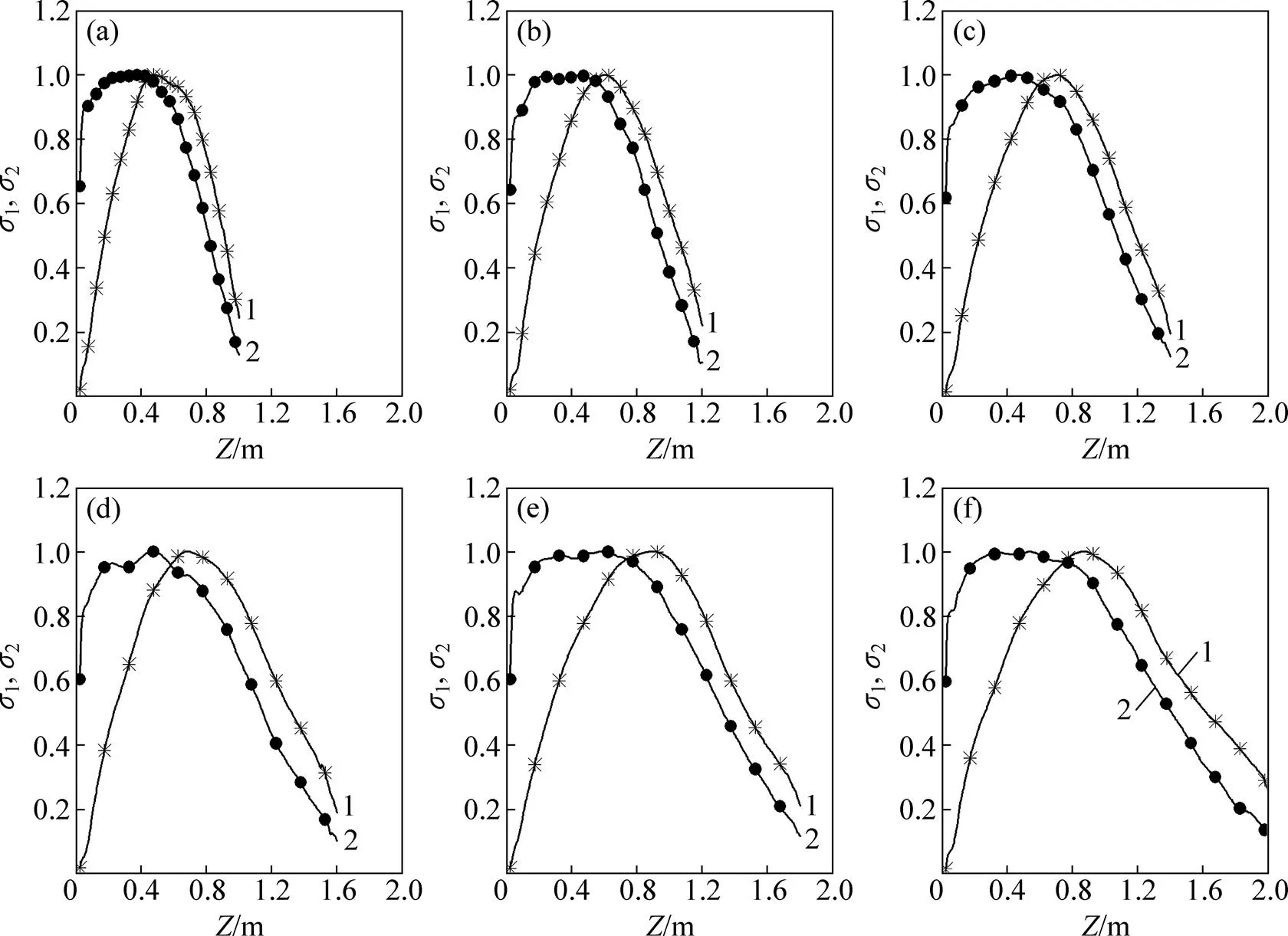
/m：(a) 1.0；(b) 1.2；(c) 1.4；(d) 1.6；(e) 1.8；(f) 2.0 1—1；2—2。

图10 速度比1和2随着高度的变化

Fig. 10 Change of1and2along with height

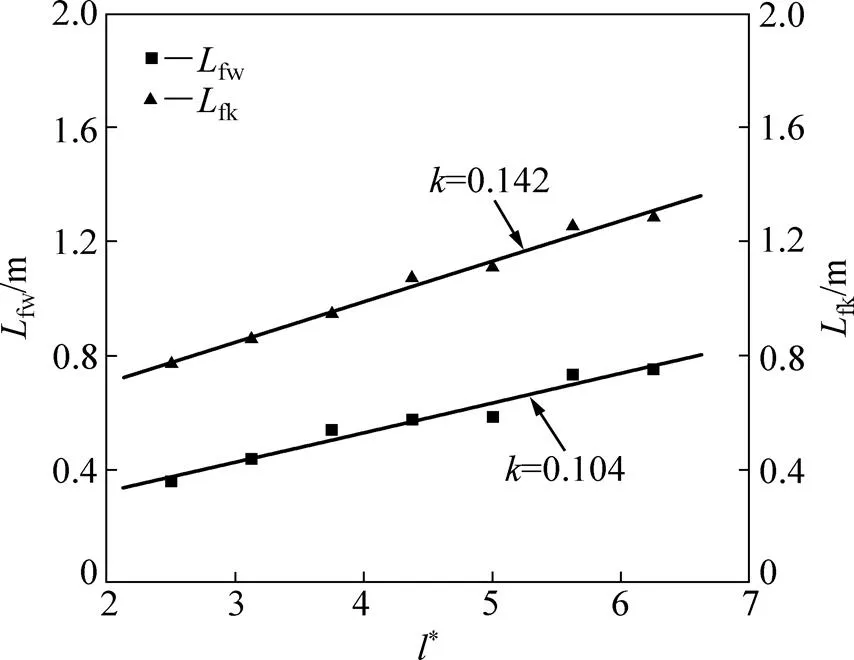
图11 不同高度通道中的Lfw和Lfk变化

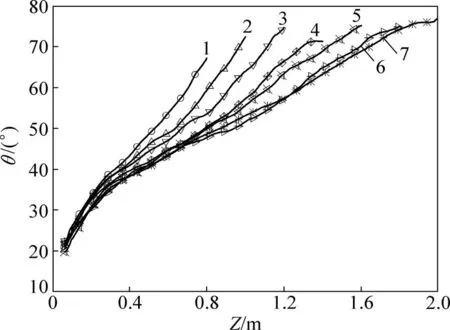
/m：1—0.8；2—1.0；3—1.2；4—1.4；5—1.6；6—1.8；7—2.0。

图12 螺旋线角度沿高度的变化

Fig. 12 Angle of spiral line variation with heights

不同高度通道内，火焰旋转较剧烈的区域高度fw和可见火焰高度fk分别对应的螺旋线角度w和k如图13所示。由图13可知：w的变化范围为41.4°~47.1°，平均值为44.7°。k的变化范围为57.5°~65.8°，平均值为60.9°。尽管通道高度不同，但w和k的变化不明显，尤其是当*大于3后。由此可以推测，在一定条件下能够利用螺旋线角度来确定旋转火焰的火焰旋转较为剧烈的区域高度及可见火焰高度。

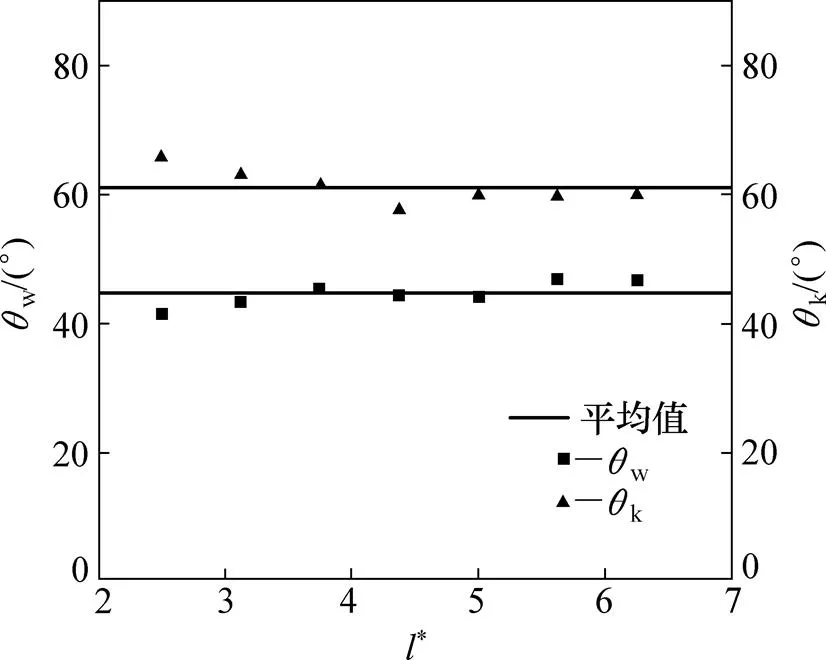
图13 不同高度通道中θw和θk的分布

3 结论

1) 竖通道高度对旋转火焰中轴线上最高温度的高度影响不大。

2) 竖通道高度增加后，中轴线上竖直向上运动的最大轴向速度和流场最大切向速度所在高度也相应升高，最大轴向速度所在高度基本都保持在通道中部附近区域，最大切向速度所在高度由通道的下部1/3高度附近区域变化至1/4高度附近区域。

3) 通道高度增加后，对流场竖直向上的轴向运动速度和流场旋转的切向速度均起到增大的作用，竖直向上运动速度增加相对更明显，竖直向上运动速度的最大值随通道高度上升的增加幅度约为最大切向速度增加幅度的1.5倍。

4) 通道高度增加后会加强通道内的旋转，提高由侧开缝向通道内引射空气的能力，但其增大的幅度要小于通道高度增加的幅度。

5) 通道高度增加后，旋转较剧烈区域高度和可见火焰高度值均有所增大，但是对可见火焰平均高度增大的作用较旋转较强烈区域更明显。

6) 不同通道高度时，旋转较为剧烈区域顶端和可见火焰顶端区域的螺旋线角度变化幅度都较小，旋转较为剧烈的区域顶端螺旋线角度平均值为44.7°，可见火焰顶端螺旋线角度平均值为60.9°。

[1] CHOW W K, HAN S S. Experimental investigation on onsetting internal fire whirls in a vertical shaft[J]. Journal of Fire Sciences, 2009, 27(6): 529−543.

[2] CHOW W K, HAN S S. Experimental data on scale modeling studies on internal fire whirls[J]. International Journal on Engineering Performance-Based Fire Codes, 2011, 10(3): 6374.

[3] LEI Jiao, LIU Naian, ZHANG Linhe, et al. Experimental research on combustion dynamics of medium-scale fire whirl[J]. Proceedings of the Combustion Institute, 2011, 33(2): 24072415.

[4] CHOW W K, HE Z, GAO Y. Internal fire whirls in a vertical shaft[J]. Journal of Fire Science, 2011, 29: 7192.

[5] HUO Y, CHOW W K, GAO Y. Internal fire whirls induced by pool fire in a vertical shaft[C]//ASME/JSME 2011 8th Thermal Engineering Joint Conference (AJTEC2011). Honolulu, Hawaii, USA, 2011: T20034-1-T20034-6.

[6] HUO Y, GAO Y, HUANG D X. Numerical simulation of internal fire whirls in an inclined shaft[J]. Advanced Materials Research, 2013, 732/733: 254257.

[7] 霍岩, 邹高万, 李树声, 等. 单侧有限宽度开缝竖通道内的旋转热流体特性[J]. 哈尔滨工程大学学报, 2014, 35(3): 320324. HUO Yan, ZOU Gaowan, LI Shusheng, et al. Characteristics of rotating thermal fluid in a vertical shaft with a confined single coner gap[J]. Journal of Harbin Engineering University, 2014, 35(3): 320324.

[8] 霍岩, 邹高万, 李树声, 等. 竖通道内液体燃料燃烧形成的旋转火焰特性[J]. 哈尔滨工业大学学报, 2014, 46(1): 7782. HUO Yan, ZOU Gaowan, LI Shusheng, et al. Characteristics of fire whirls induced by liquid fuel in a vertical shaft[J]. Journal of Harbin Institute of Technology, 2014, 46(1): 7782.

[9] 霍岩. 有限开口空间热驱动流大涡模拟和实验研究[D]. 哈尔滨: 哈尔滨工程大学航天与建筑工程学院, 2010: 815.HUO Yan. Research on thermal fluid in partially open enclosure by large eddy simulation and experiments[D]. Harbin: Harbin Engineering University. College of Aerospace and Civil Engineering, 2010: 815.

[10] CHUAH K H, KUWANA K, SAITO K, et al. Inclined fire whirls[J]. Proceedings of the Combustion Institute, 2011, 33: 24172424.

[11] HUGGETT C. Estimation of rate of heat release by means of oxygen consumption measurements[J]. Fire and Materials, 1980, 4(2): 6165.

[12] PRASAD K, LI C, KAILASANATH K, et al. Numerical modelling of methanol liquid pool fires[J]. Combustion Theory and Modelling, 1999, 3(4): 743768.

[13] MILAN Z, VLASTIMILR R. Heat capacity of liquid-heptane converted to the international temperature scale of 1990[J]. Journal of Physical and Chemical Reference Data, 1994, 23(1): 5561.

[14] WERNER H, WENGLE H. Large-eddy simulation of turbulent flow over and around a cube in a plate channel[C]//8th Symposium on Turbulent Shear Flows. Munich, Germany, 1993: 155168.

[15] WANG Huiying. Numerical study of under-ventilated fire in medium-scale enclosure[J]. Building and Environment, 2009, 44(6): 12151227.

[16] PEACOCK R D, RENEKE P A, DAVIS W D, et al. Quantifying fire model evaluation using functional analysis[J]. Fire Safety Journal, 1999, 33: 167184.

(编辑 赵俊)

Effects of shaft height on heat flow field of fire whirls in vertical shaft

HUO Yan, HUANG Dexiang, ZOU Gaowan, LI Shusheng

(College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China)

Taking a square vertical shaft with bottom side length of 0.32 m as research object, the swirling flames heat field of a shaft with height of 0.8−2.0 m was simulated. The effects of shaft height on the temperature, the tangential rotational velocity and the vertical velocity of the upward movement were studied. The results show that increasing the height of the shaft is to strengthen the rotation of the inner passage of the flame and increase the capacity of the injection of air to the shaft through the corner gaps. However, the angle of spiral line at the top of intense rotational zone and the tip of visible flame are less affected by the height of shaft, and the mean angles are 44.7° and 60.9°, respectively.

fire whirls; vertical shaft height; heat flow field

10.11817/j.issn.1672-7207.2016.12.034

TU998.1；X932

A

1672−7207(2016)12−4224−07

2015−12−24；

2016−04−07

国家自然科学基金资助项目(51676051，11402061)；黑龙江省博士后科研启动基金资助项目(LBH-Q13043)；中央高校基本科研业务费专项基金资助项目(HEUCF160201)(Projects(51676051, 11402061) supported by the National Natural Science Foundation of China; Project(LBH-Q13043) supported by Heilongjiang Postdoctoral Funds for Scientific Research Initiation; Project(HEUCF160201) supported by Fundamental Research Funds for the Central Universities)

霍岩，副教授，从事火灾动力学研究；E-mail：huoyan205@126.com