采用分段法研究含镁球团等温还原过程动力学

青格勒，吴铿，员晓，刘起航，杜瑞岭，闫广



采用分段法研究含镁球团等温还原过程动力学

青格勒1, 2，吴铿1，员晓1，刘起航3，杜瑞岭1，闫广1

(1. 北京科技大学钢铁冶金新技术国家重点实验室，北京，100083；2. 首钢技术研究院，北京，100041；3. 西安建筑科技大学冶金工程学院，陕西西安，710055)

为了研究MgO添加剂对球团矿还原行为的影响以及确定还原反应过程动力学机理，采用球团矿的等温还原标准检验方法，测定3种不同含镁球团的还原性能，考察还原度与还原速率的变化情况。采用分段法对其还原反应过程动力学进行分析，确定反应过程前期和后期不同的动力学机理函数积分式，进而通过建立动力学模型，计算不同阶段的反应速率常数。研究结果表明：前期还原过程反应速率常数受镁含量影响较大，而后期浮氏体还原过程的反应速率常数则受镁含量的影响不大。

分段法；球团矿；还原动力学；反应速率常数

酸性球团在高炉的使用量逐年增加，但国内球团矿的SiO2含量普遍较高，这不仅影响球团矿的还原性，而且会提高燃料比[1]。国内外研究表明低硅球团添加高镁精矿可以改善球团矿的高温冶金性能，鲜有学者对其还原反应过程动力学机理进行分析[2−6]。球团矿的还原过程可以看成是由气体的扩散和化学反应等不同控速步骤组成，研究其动力学常采用稳态处理 法[7−8]，而且其还原过程的前期主要为Fe2O3→FeO的还原，反应后期则以FeO→Fe的还原过程为主，因此，采用单一的模型机理并不能准确地反映铁氧化物的还原过程[9]。分段尝试法为冶金反应工程学研究反应过程动力学的新方法，以“三传一反”为基础理论，采用分段尝试法来确定反应过程动力学的机理、动力学参数以及不同控制环节[10−12]。本文作者采用分段尝试法，在不同阶段采用不同的反应机理对含镁球团矿还原试验结果进行拟合，确定出不同阶段的反应机理，并以此为依据，从冶金传输原理的质量传输和化学反应的基本原理出发，针对还原过程中不同阶段建立反应动力学模型，计算得到不同阶段的动力学参数，分析镁含量变化对还原特性的影响。

1 还原试验

1.1 试验原料

本试验所用3种不同镁含量的球团在为实验室条件下制取，利用化学分析对球团矿进行检测，其化学成分见表1。

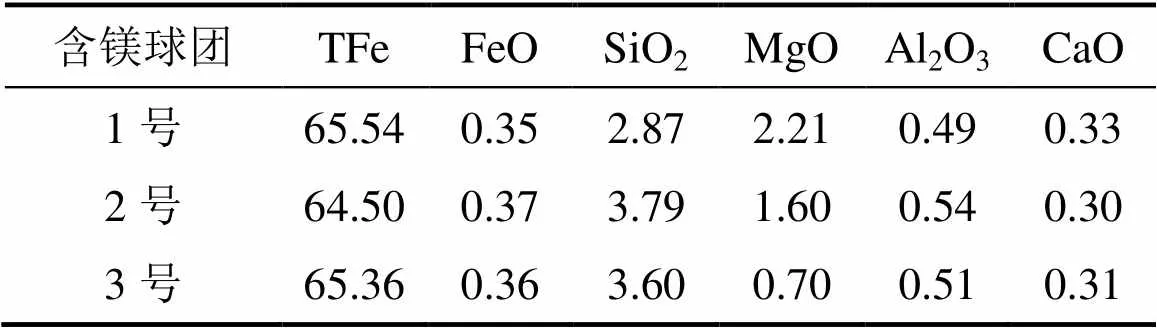
表1 3种球团矿的主要化学成分(质量分数)

1.2 实验方法

3种含镁球团矿是用高品位、SiO2质量分数低的磁铁矿粉添加不同比例含镁添加剂黏结剂，在直径为800 mm的圆盘造球机上进行造球。造球时间为10 min，造球后选择直径为10~12.5 mm的生球进行焙烧试验。生球团烘干后放入升温至800 ℃管式电炉，按规定的焙烧温度梯度升温至1 280 ℃进行焙烧，并在该温度下焙烧时间20 min，成品球抗压强度分别为 3 267，3 305和3 212 N/个。

实验采用球团矿还原性标准检验(GB 13241—91)方法。以3价铁状态为基准，即假设铁矿石的铁全部以Fe2O3形式存在，并把这些Fe2O3中的氧含量(质量分数)算作100%，以还原180 min的失氧量与全氧量比值来计算铁矿石还原度，进一步将还原度对时间求导数得到还原速率d/d。

将随机选取的500 g粒度范围为10~12.5 mm的球团矿试样装入反应容器中，并置于还原炉内。在温度从室温升到反应温度过程中，通入保护气N2，流量为6 L/min。当还原炉内温度达到指定的温度时，将保护气改为配好的由CO和N2组成的还原气体，CO和N2体积比为3:7，流量为15 L/min，然后开始等温还原180 min，由计算机连续记录试样的质量损失变化。

2 试验结果与分析

在1 173 K时，实验条件下3种球团矿的还原度与时间的关系曲线见图1。从图1可见：在试验所涉及的温度范围内，随着恒温时间增加，球团矿的还原度也逐渐增加，但反应前期还原度迅速增加，随后还原度增幅逐渐变小，在反应后期趋于平稳。在还原180 min后，3种含镁球团的还原度分别为67%，63%和51%。

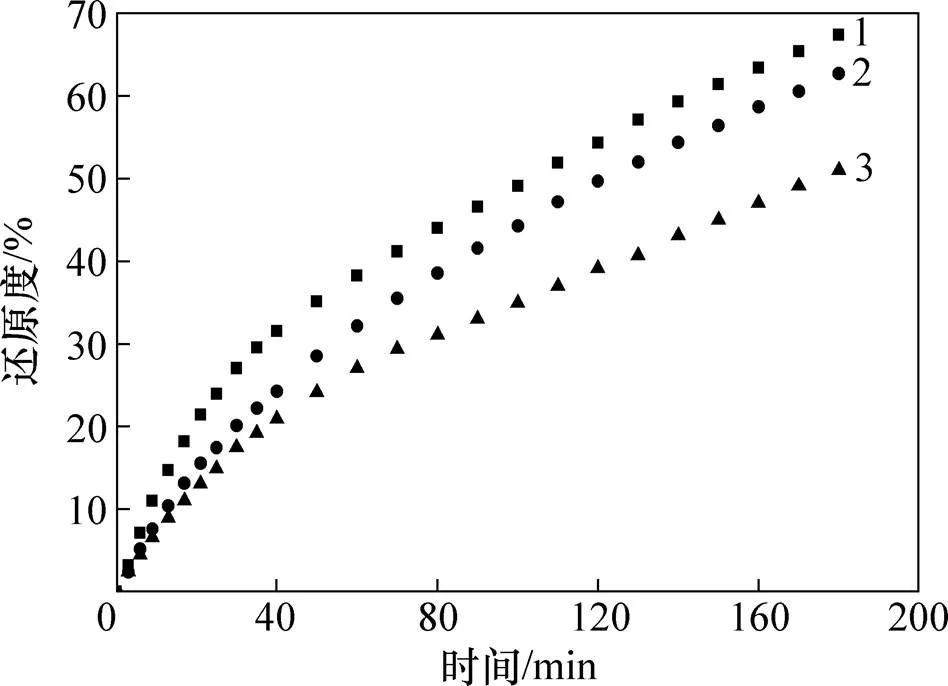
1—1号含镁球团；2—2号含镁球团；3—3号含镁球团。

图1 3种球团矿还原度与时间的关系曲线

Fig. 1 Relation curves of reduction degree and time of three kinds of pellets

3种不同含镁球团还原速率随时间变化关系见图2。由图2可以看出：3种球团矿还原速率曲线随时间的变化趋势一致；反应刚开始，还原速率迅速增加，当反应进行到6 min左右后还原速率达到最大，之后又急剧减小，随后，反应进行到后期还原速率变化缓慢。分析原因可知，还原刚开始完全为Fe2O3的还原过程，随着还原进行，球团体积不断膨胀，气体可以扩散深入到球团内部，能够进行反应的内部小颗粒也不断增加，使得反应速率提高。反应进行到6 min左右后，随着反应进行，颗粒反应面积不断减小，反应速度随之降低。当反应进行到后期，大部分Fe3O4反应消失，此时主体反应物为FeO与MgO形成的无限互溶固溶体，此时还原最难进行，反应速率较慢，需要较长还原时间。

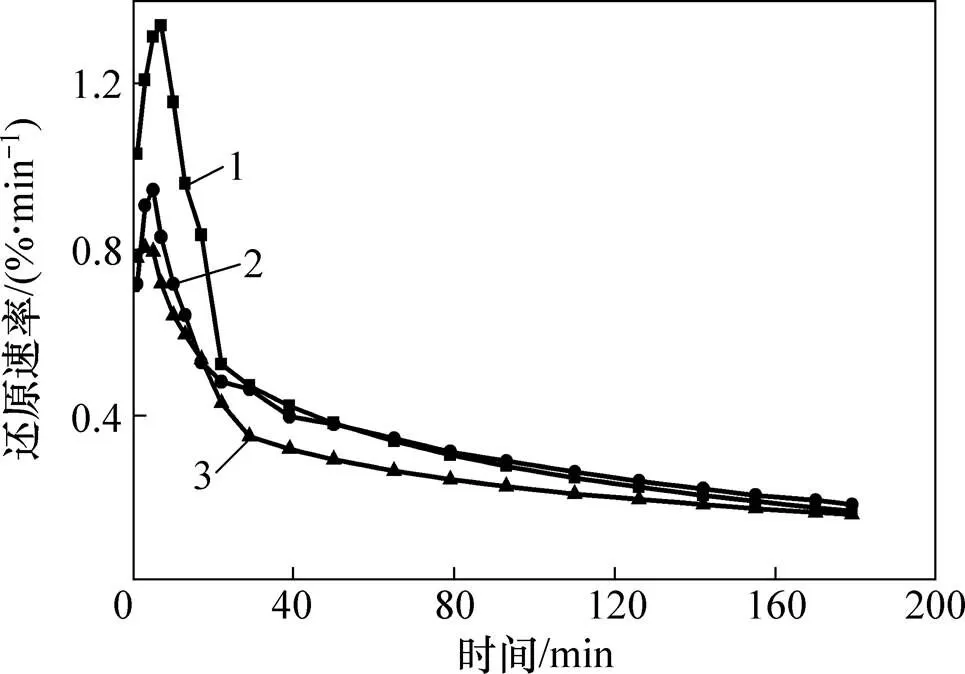
1—1号含镁球团；2—2号含镁球团；3—3号含镁球团。

图2 3种球团矿的还原速率与时间的关系曲线

Fig. 2 Relation curves of reduction rate and time of three kinds of pellets

根据铁矿石还原热力学分析，Fe3O2的还原是分级进行的，而浮氏体的还原阶段是阻力最大的环节，所以，以往大量研究Fe2O3还原只考虑最后一步FeO的还原过程。但对于含镁球团还原过程，由于大量铁酸镁的存在导致其还原性能与反应前期还原动力学密切相关，所以，需要考虑还原前、后期还原过程动力学。根据还原速率变化曲线可知：1号和2号含镁球团的还原速率在22 min后开始变化缓慢，因此，将22 min作为反应前后期分界点；而3号含镁球团的还原速率在27 min后才开始变化缓慢，因此，将27 min作为其反应前后期的分界点。实际球团矿的还原在不同还原阶段内的反应是不一样的，反应前期主要为Fe2O3还原生成浮氏体过程，此时还原速率较快，进入反应后期，则以浮氏体的还原过程为主，此时还原速率 较低。

3 含镁球团还原过程不同阶段动力学模型

基于热分析动力学，在等温条件下，动力学方 程[13]为

()=(1)

式中：()为反应机理函数的积分形式；为反应速率常数，s−1；为时间，s。

等温法中，对于某一简单反应来说，速率常数(T)是一常数，通过代入不同的机理函数积分式，对其进行拟合，选取能令直线线性最佳的()，即为最合适的机理函数。从球团矿还原特点出发，选取6种常用的机理函数积分式，采取逐一尝试的方法，对反应前、后期数据代入反应模型机理函数积分形式进行计算，然后拟合()−直线，选取拟合直线线性度最大的机理函数为这一阶段的控制模型函数。此实验中以还原度代替动力学方程的转化率，拟合结果见表2。

3.1 反应过程前期动力学模型

由表2拟合结果可知：此阶段的最佳反应机理函数积分式()=(1−)−2/3−1，即为多颗粒的一级球状化学反应模型控速。添加MgO球团经焙烧后，其总孔隙度、孔径随MgO含量升高而增加[14]，使得多孔球团反应前期气体扩散阻力减小，并且固相产物层还较薄，相对来说化学反应的阻力比其他步骤大，此时反应最可能由化学反应控制。

此阶段反应动力学模型推导如下。

对于一级球状化学反应，转化率的表达式为

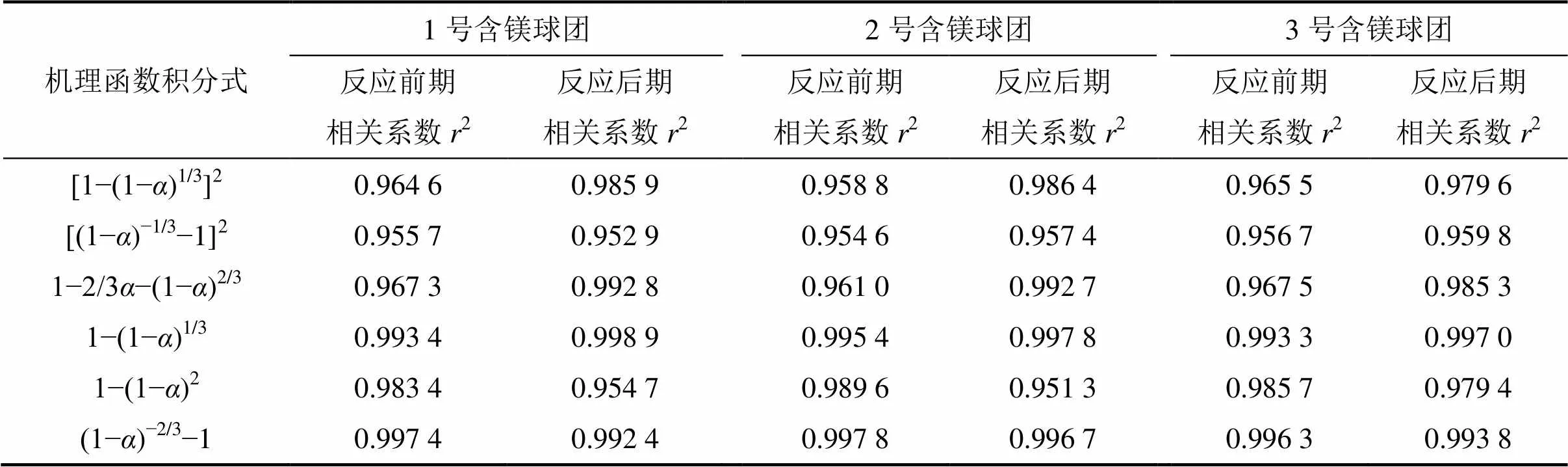
表2 常用机理函数拟合参数

其中：0为颗粒初始半径，m；R为某一还原转化率下的半径，m。

单一颗粒的反应截面积为

体系内单位质量的颗粒数为

总的反应面积为

由此可知：

其中：ρ为球团矿的密度，kg/m3；rea为反应速率常数，kg/(m2·s­)。

当=0时，=0，积分得：

可得化学反应速率常数与斜率的关系为

通过对(1−)−2/3−1与时间进行拟合可以得到拟合直线斜率，代入式(8)即可计算出化学反应速率 常数。

3.2 反应过程后期动力学模型

由表2拟合结果可知：此阶段的最佳反应机理函数积分式()=1−(1−)1/3，即采用收缩核界面化学反应控速模型来拟合实验数据可以较好地描述后期的反应机理。分析还原过程可知，随着反应进行，后期则进入浮氏体的还原阶段，由热力学分析可知浮氏体较难还原，所以此时化学反应最有可能成为该反应过程的控速环节。

反应后期只考虑FeO还原为Fe的反应，即

CO+FeO=Fe+CO2

ΔΘ=−13 160+17.21(9)

球形颗粒反应速率为

未反应核体积内反应物的反应速率为

据式(10)与式(11)，分离变量积分可得

式中：FeO为FeO的密度，kg/m3，0为反应物原始半径，m；FeO为FeO的摩尔质量，kg/mol；CO为CO的浓度，mol/m3。

由ΔΘ=−lnΘ可得平衡常数，再根据Θ=CO2/CO得出CO，由=得CO。将数据代入可计算出不同温度下的化学反应常数。

4 不同阶段动力学参数计算与分析

还原前期，根据3.1节中对反应模型推导结果，将前期数据代入式(7)进行线性拟合得到拟合直线斜率，将球团密度ρ=4.93×103kg/m3，颗粒半径0=5.5×10−3 m代入式(8)可计算出不同球团矿的反应前期化学反应速度常数。同理，根据还原后期动力学模型，拟合得到直线斜率，将相关动力学参数代入式(12)可计算得到还原后期的反应速率常数。生球经过高温氧化焙烧后，主要成分为Fe2O3和铁酸镁(Fe2O3·MgO)，可以看出前期反应多且复合进行，不同反应物以及中间产物的还原特性也不同，本文将前期还原过程认为是Fe2O3→FeO的总反应，根据模型拟合计算出的反应速率常数为整个还原前期的综合反应速率常数。3种球团还原前后反应速率常数计算结果见表3。

从表3可以发现：反应前期随着镁质量分数增加(即从3号含镁球团至1号含镁球团)，反应速率常数升高，前期反应速率常数受镁含量影响较大，而后期反应速率则受镁含量的影响不大，其中MgO质量分数为0.7%的3号含镁球团的反应速率常数比前2种球团的稍低。从成分上看，这是由于MgO质量分数的提高，使得焙烧后球团含有较多的铁酸镁且铁酸镁的还原性能较好，而难还原的铁橄榄石则较少，从而改善了球团矿前期还原特性。根据前面结果可知：前期还原反应由多颗粒一级界面化学反应控速，后期浮氏体还原由收缩核界面化学反应控速。从整个球团矿还原过程来看，反应前期还原速率较快，限制其还原速率的是反应后期浮氏体的界面化学反应控速。

表3 CO还原球团矿过程中反应动力学的相关参数

5 结论

1) 根据球团矿还原特点，由分段尝试法确定了反应前后期的反应动力学机理。前期反应主要为Fe2O3的还原生成浮氏体，采用多颗粒一级球状化学反应模型来描述这个过程，后期反应主要为浮氏体的还原，采用收缩核界面化学反应模型。

2) 前期Fe2O3→FeO这一还原过程的反应速率常数受镁含量影响较大，而后期浮氏体还原过程的反应速率常数则受镁含量的影响不大。

3) 采用分段法研究MgO含量对球团矿前后期还原行为的影响，对研究其他金属氧化物还原性能有一定借鉴意义。

[1] MATSUMURA M, HOSHI M, KAWAGUCHI T. Improve of sinter softening property and reducibility by controlling chemical compositions[J]. ISIJ International, 2005, 45(4): 598−607.

[2] 姜涛, 何国强, 李光辉, 等. 脉石成分对铁矿球团还原膨胀性能的影响[J]. 钢铁, 2007, 42(5): 7−11.JIANG Tao, HE Guoqiang, LI Guanghui, et al. Effect of gangue composition on reduction swelling of iron ore pellets[J]. Iron and Steel, 2007, 42(5): 7−11.

[3] 陈铁军, 张一敏. 镁橄榄石用于铁矿球团的试验研究[J]. 矿产保护和利用, 2005(3): 43−48. CHEN Tiejun, ZHANG Yimin. Experimental study on application of forsterite to pelletization[J]. Conservation and Utilization of Mineral Resources, 2005(3): 43−48.

[4] 范晓慧, 甘敏, 陈许铃, 等. 低碱度镁质氧化球团的试验研究[J]. 钢铁, 2009, 44(3): 6−10. FAN Xiaohui, GAN Min, CHEN Xuling, et al. Experiments of low-basicity magnesian oxided pellets[J]. Iron and Steel, 2009,44(3): 6−10.

[5] 吴钢生. 碱性含镁球团矿的应用及合理炉料结构研究[J].钢铁, 2006, 41(12): 19−26. WU Gangsheng. Use of magnesium-bearing basic pellet and reasonable burden design[J]. Iron and Steel, 2006, 41(12): 19−26.

[6] 高强健, 沈峰满, 郑海燕, 等. MgO对铁矿球还原冶金性能的影响[J]. 东北大学学报(自然科学版), 2014, 35(12): 1742−1745.GAO Qiangjian, SHEN Fengman, ZHENG Haiyan, et al. Investigation on effect of MgO on reduction metallurgical properties of iron ore pellet[J]. Journal of Northeastern University(Natural Science), 2014, 35(12): 1742−1745.

[7] 吴铿, 张家志, 赵勇, 等. 冶金反应工程学中反应过程动力学的研究方法探究[J]. 有色金属科学与工程, 2014, 5(4): 1−6. WU Keng, ZHANG Jiazhi, ZHAO Yong, et al. Research methods on the reaction kinetics of metallurgical reaction engineering[J].Nonferrous Metals Science and Engineering, 2014, 5(4): 1−6.

[8] 张建良, 王振阳, 邢相栋, 等. 基于Energiron的球团矿气体还原动力学及其机理[J]. 中南大学学报(自然科学版), 2015, 46(1): 41−48. ZHANG Jianliang, WANG Zhenyang, XING Xiangdong, et al. Kinetics and mechanism of gas-based reduction of pellets based on Energiron[J]. Journal of Central South University(Science and Technology), 2015, 46(1): 41−48.

[9] 程红伟, 鲁雄刚, 李谦. 含碳球团还原动力学机理[J]. 中国稀土学报, 2008, 26(8): 103−107. CHENG Hongwei, LU Xionggang, LI Qian, et al. Reduction kinetics mechanism of iron ore pellets containing graphite[J]. Journal of the Chinese Rare Earth Society, 2008, 26(8): 103−107.

[10] 潘文, 吴铿, 赵霞, 等. 首钢烧结矿还原动力学[J]. 北京科技大学学报, 2013, 35(1): 35−40.PAN Wen, WU Keng, ZHAO Xia, et al. Reduction kinetics of Shougang iron ore sinter[J]. Journal of University of Science and Technology Beijing, 2013, 35(1): 35−40.

[11] 吴铿, 折媛, 朱利, 等. 对建立冶金反应工程学科体系的思考[J]. 钢铁研究学报, 2014, 26(12): 1−8. WU Keng, SHE Yuan, ZHU Li, et al. Consideration on the subject system of metallurgical reaction engineering[J]. Journal of Iron and Steel Research, 2014, 26(12): 1−8.

[12] 吴铿, 刘起航, 湛文龙, 等. 分段法研究焦油析出动力学过程的探索[J]. 中国高校化工学报, 2014, 28(5): 33−39.WU Keng, LIU Qihang, ZHAN Wenlong, et al. Research on tar precipitation kinetics using phasewise analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2014, 28(5): 33−39.

[13] 胡荣祖. 热分析动力学[M]. 北京: 科学出版社, 2001: 8−11. HU Rongzu. Thermal analysis kinetics[M]. Beijing: Science Press, 2001: 8−11.

[14] EL-GEASSY A A. Gaseous Reduction of MgO-doped Fe2O3compacts with carbon-monoxide at 1 173−1 473 K[J]. ISIJ International, 1996, 36(11): 1328−1337.

(编辑 杨幼平)

Isothermal reduction kinetics of magnesium containing pellets by sectioning method

QING Gele1, 2, WU Keng1, YUN Xiao1, LIU Qihang3, DU Ruiling1, YAN Guang1

(1. State Key Laboratory of Advanced Metallurgy, University of Science and Technology Beijing, Beijing 100083, China;2. Shougang Institute of Technology, Beijing 100041, China;3. School of Metallurgical Engineering, Xi'an University of Architecture &Technology, Xian 710055, China)

In order to study the influence of MgO on reduction behavior of pellets and find the kinetic mechanisms, isothermal reduction experiment of three kinds of magnesium-containing pellets was done to research the reduction performance by weight loss method. Furthermore, the change of reduction degree and reduction rate was examined. The kinetics of reduction was analyzed by sectioning method, and two different kinetic mechanisms were found respectively at initial stage and later stage. Based on this, the dynamic models of different reaction stages were established, and the reaction rate constants were obtained. The results show that the reaction rate constant at initial stage is influenced significantly by the content of MgO. However, the content of MgO has less influence on the reaction rate of FeO reduction at later stage.

sectioning method, pellets, reduction kinetics, reaction rate constant

10.11817/j.issn.1672-7207.2016.12.002

TF512

A

1672−7207(2016)12−3977−05

2015−12−16；

2016−03−30

国家自然科学基金资助项目(51274026, 51474022)；钢铁冶金新技术国家重点实验室自主研发项目(41603003)；国家高技术研究发展计划(863计划)项目(2009AA06Z105)(Projects(51274026, 51474022) supported by the National Natural Science Foundation of China; Project(41603003) supported by the Independent Research Project of State Key Laboratory of Advanced Metallurgy; Project (2009AA06Z105) supported by the National High Technology Research and Development Program (863 Program) of China)

吴铿，博士，教授，从事高炉炼铁研究；E-mail：wukeng1030@sina.com