关于图值随机元序列的强极限定理
2017-01-19汪忠志李文喜
汪忠志,李文喜
(安徽工业大学数理科学与工程学院,安徽马鞍山243002)
关于图值随机元序列的强极限定理
汪忠志,李文喜
(安徽工业大学数理科学与工程学院,安徽马鞍山243002)
本文研究在局部连通图中取值的随机元的r-阶均值集、r-阶广义样本均值集的基本性质及其极限性质.利用关于随机元的分离引理以及随机游动的常返性,得到了关于图值随机元序列广义强大数定理.推广了已有的结果.
强大数定律;图;r-阶权函数;r-阶均值集;r-阶广义样本均值;随机游动
1 引言
概率极限理论是概率论的重要分支之一.经典的极限理论曾经是概率论研究的中心课题,近现代极限理论的研究至今方兴未艾.自上世纪30年代以来,许多学者致力于将概率论推广到各种数学结构中.著名概率学家Love在阐述概率论的基本特征时曾指出“到今天,概率论在数学上已经发展的充分成熟,于是就呈现出来这样一种预兆,即要摆脱这些限制而考虑从测度空间到愈益抽象的空间的更一般的函数族······”.关于抽象空间上的概率理论的研究,可以上溯到1935年Kolmogorov[1]关于Banach空间上的概率分布的特征泛函以及1948年Frchet[2]关于Banach空间上的Gauss分布的工作.
关于抽象空间上的随机元的定义,有多种不同的方式.在一般情况下,它们还确实是彼此不同的概念.不同的定义有各自的优缺点,分别适应研究不同问题的需要.对取值于抽象空间上的随机元的随机过程的合理解释与深刻的应用激发了许多学者对一般拓扑空间上的概率的研究,而研究的关键是给出随机元“均值”(平均)的合理定义以及相应的收敛性概念.
Banach空间上的随机元x1,x2,···,xn的均值可以自然地定义为n-1(x1+x2+···+xn),利用Galfand-Pettis积分可以定义随机元的均值(期望)(参见文[3]).与线性空间不同,在一般(非线性)拓扑空间中,必须寻找合适的途径来定义随机元的“均值”以及相应的收敛性概念.Frchet在文[2]中讨论了一般度量空间上的概率,并且给出了完备度量空间(X,d)上关于概率测度µ的均值(亦称Frchet均值)的定义.即设ξ:Ω→X是定义在概率空间(Ω,F,P),在(X,d)中取值的随机元.令
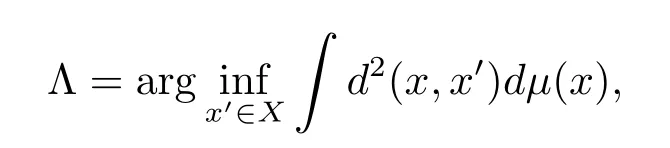
称Λ为随机元ξ的均值集(Frechet均值).
可以看出这个定义显然是包含了最小二乘法的基本思想.最早获得度量空间上随机元的极限定理的是Ziezold,他(她)在文[4]中讨论了可分拟度量空间上的随机元的强大数定律,随后Sverdrup–Yhygeson[5]讨论了取值于连通紧空间上的随机元的强大数定律, Bhattacharya和Patrangenaru[6]给出了有界子集均为紧子集的度量空间上的随机元的极限定理,推广了Ziezold[4]的结果.最近,Natalia Mosina[7,8]等给出了在图与群上取值的随机元的一个新的概率框架,讨论了随机元均值集(期望)的若干性质及大数定律,并用在辫群(Braid group)上取值的随机元的均值集和大数定律,破解了一个基于辫群上共轭元的难解问题的零知识证明协议,这在密码学上具有十分重要的意义.
本文在文献[7]的基础上,提出了在局部有限图上取值的随机元的r-阶权函数、r-阶均值集以及r-阶广义样本均值集等概念,讨论了其基本性质,并且就随机元的均值集是单点集和两点集情形,获得了关于图值随机元序列的广义强大数定理.
2 预备知识
设(Ω,F,P)是固定的概率空间,Γ=(V(Γ),E(Γ))是局部有限图.考虑定义在可测空间(Ω,F)上且在Γ的顶点集中取值的随机元ξ:Ω→V(Γ).
假设µ是由随机元ξ在V(Γ)的原子上诱导出的概率测度
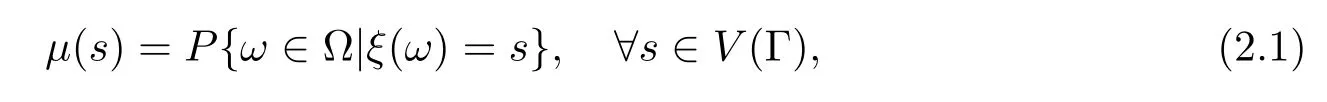
记为µξ(·).
现在在新的概率空间(V(Γ),S,µ)上来研究随机元ξ:Ω→V(Γ).
定义2.1设∀v∈V(Γ).令
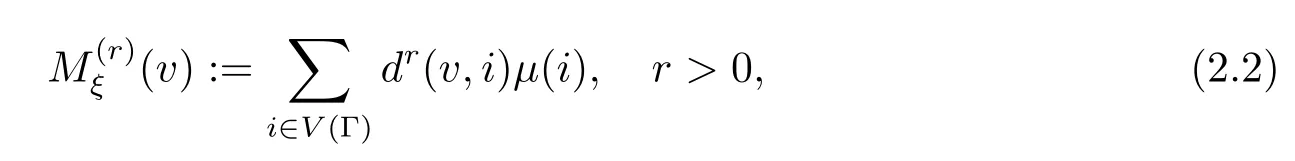
称之为v关于测度µ的r-阶权函数,其中d(v,i)表示v与i在Γ中的距离.
注一般来说,权函数并不总是有限的.本文中如无特别说明,总假设M(r)(·)<∞(r>0),即M(r)(·)在V(Γ)的每一点都有定义.
定义2.2设(V(Γ),S,µ)为所考虑的概率空间,ξ:Ω→V(Γ)是随机元,r>0.令
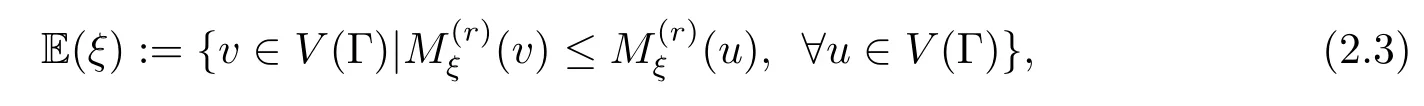
并称之为随机元ξ的r-阶均值集.
注值得注意的是,如果在(2.3)式中分别令r=2,r=1,r→0以及r→∞,上述定义的均值集(期望)可以导出对应于Euclidean空间中随机变量的均值、中位数、众数以及中列数.

令
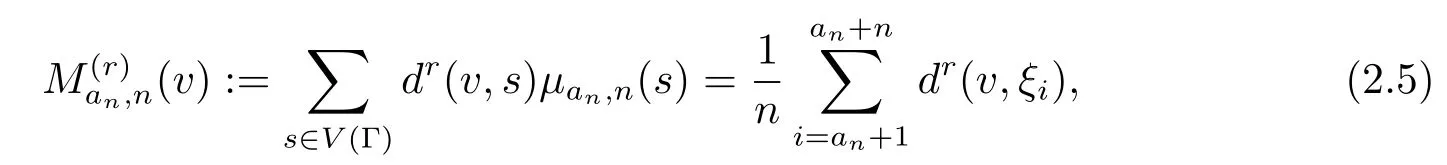
定义2.3集

为了以下证明的需要,给出几个基本引理.
引理2.1设Γ是连通图,u,v∈V(Γ).如果M(r)(u)<∞,则M(r)(v)<∞.
证令d(u,v)=d,由三角形不等式
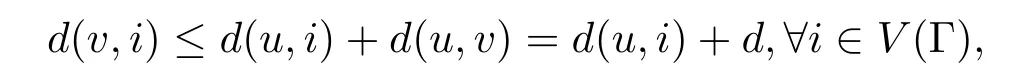
有
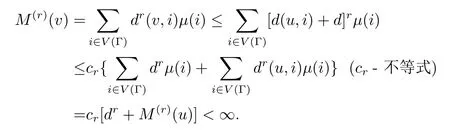
推论2.1设(V(Γ),S,µ)是所考虑的概率空间,Γ是连通图,ξ:Ω→V(Γ)是Γ上的随机元,则

或domain(M)=φ.
引理2.2设ξ:Ω→V(Γ)是Γ-值随机元,其中Γ是局部有限的连通图且r-阶权函数<∞,则均值集E(ξ)非空且有限.
证对任意固定的顶点v∈Γ,其权函数
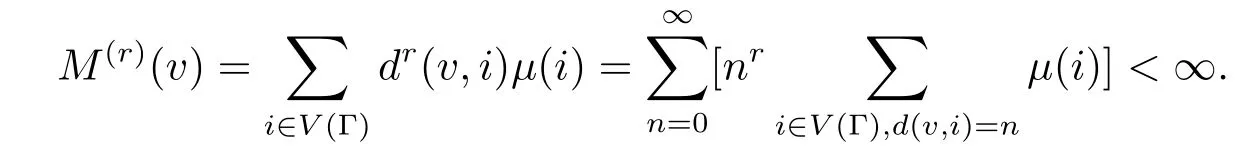
选取R∈N,使得
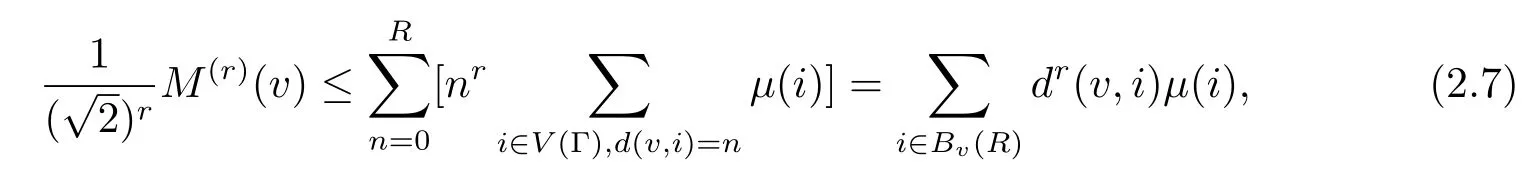
其中

是Γ中以v为中心R为半径的球.
选取u∈V(Γ),使得d(u,v)≥3R.利用三角形不等式及(2.7)式,有
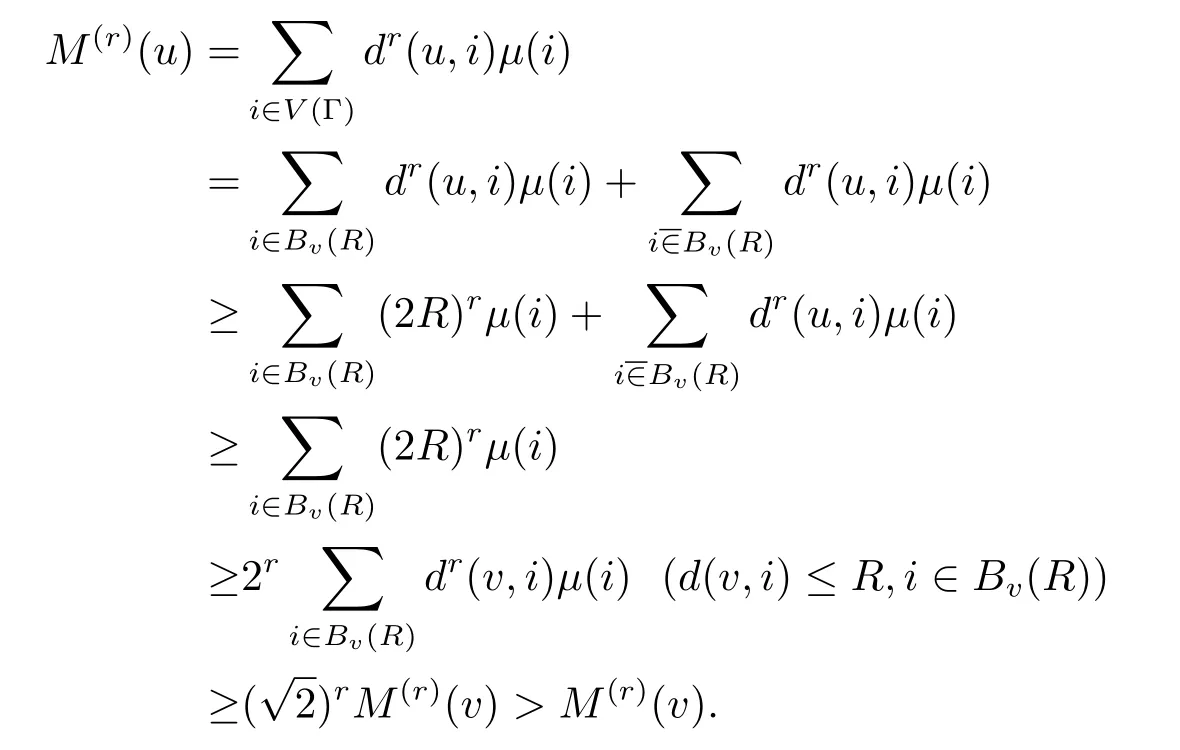
引理2.3[9]设是i.i.d.随机序列,且E(ξ1)<∞,是一列正整数,则
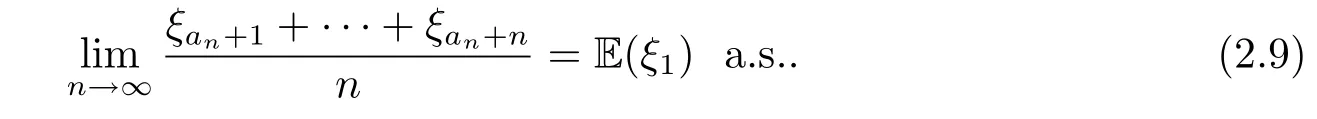
引理2.4设Γ是局部有限的连通图,v∈V(Γ),是一列i.i.d.Γ值随机元,即 ξi:Ω→V(Γ),i=1,2,···,并且<∞.则
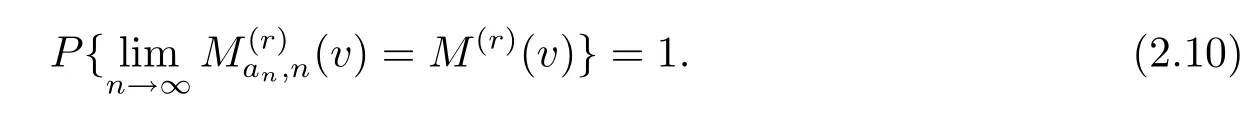
证对∀v∈V(Γ),M(r)(v)==Edr(v,ξ1).注意到由引理2.3即得结论成立.
值得注意的是引理2.4中的收敛并不是一致地成立,即对局部有限(或无限)图上的分布µ,及某些ε>0,可能有

引理2.5[10,11]设是一列i.i.d.随机变量,且Eξ1=0,E|ξ1|<∞.令R(n)=n=1,2,···,则随机游动是常返的.
引理2.6(分离引理)设Γ是局部有限的连通图,v∈V(Γ),是一列i.i.d.Γ值随机元,即ξi:Ω→V(Γ),i=1,2,···.如果<∞,则
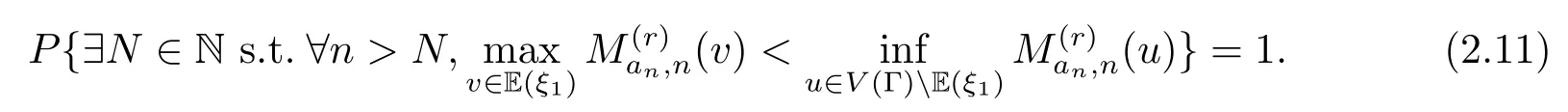
证欲证(2.11)式,只须证存在δ>0,使得
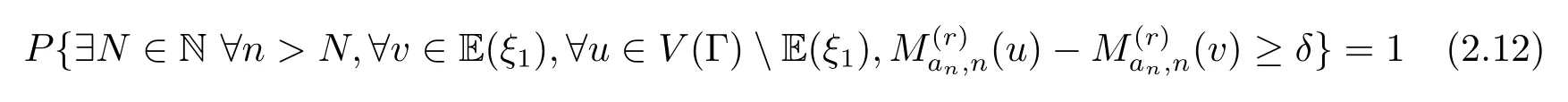
成立即可.
本文分两步来完成.首先证对固定的v0∈E(ξ1)以及充分大的m>0,有
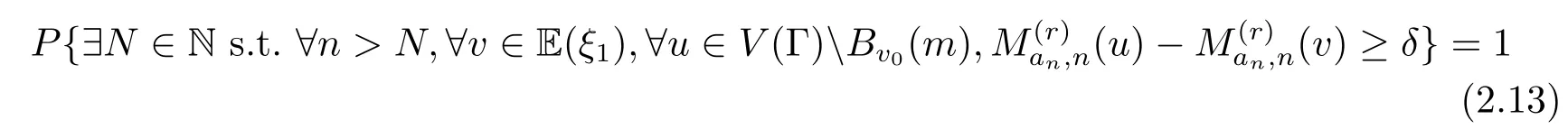
成立.其次证明
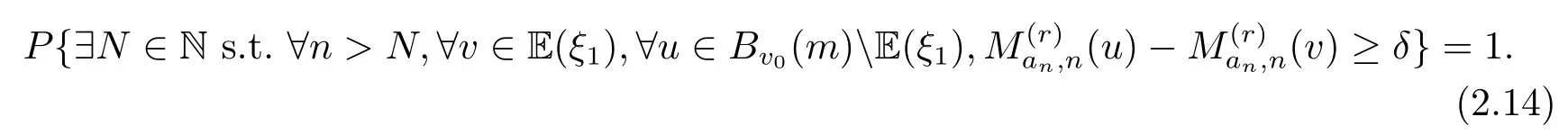
由测度的σ-可加性即得(2.11)式成立.
设v0∈E(ξ1).因M(r)(v0)<∞,如引理2.2中的做法选取R∈R,使得令m=3R.由引理2.2的证明过程可知,如果u满足d(u,v0)≥3R,则
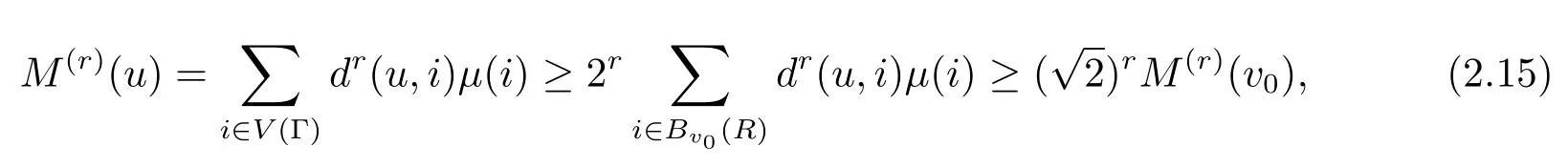
由此可知E(ξ1)⊆Bv0(3R).
因为Γ是局部有限的,所以Bv0(R)是有限的.∀ε>0,令
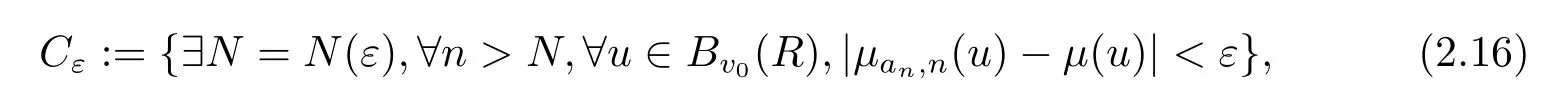
由关于随机变量µan,n(u)=的强极限定理可知,当n→∞时,µan,n(u)→ µ(u)a.s.,因而P(Cε)=1.特别的,取

而且事件Cε∗是集
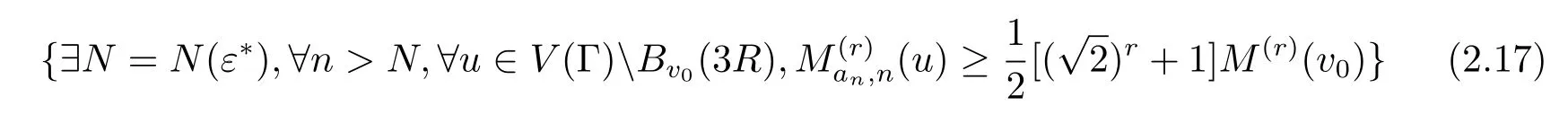
的子集.事实上,在(2.16)式定义的集合Cε∗上有利用上述结论以及(2.15)式,有
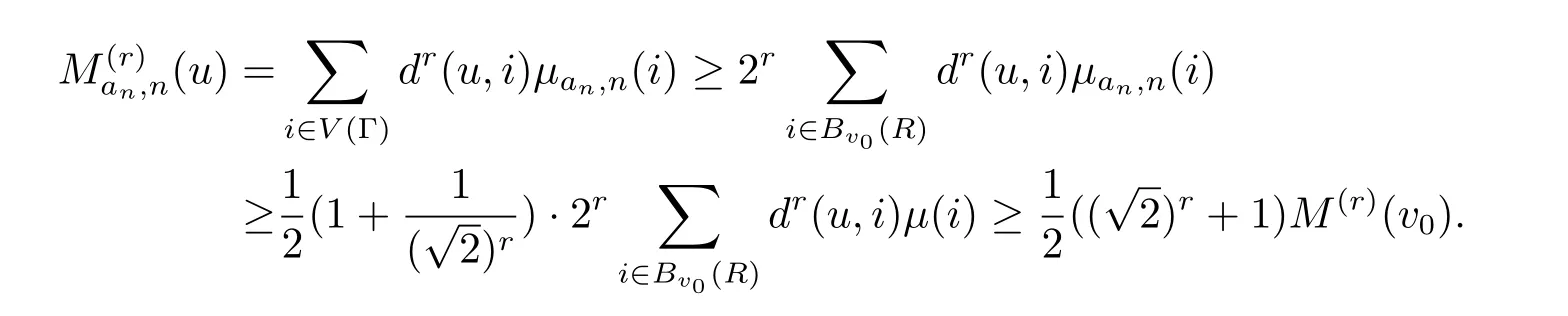
于是
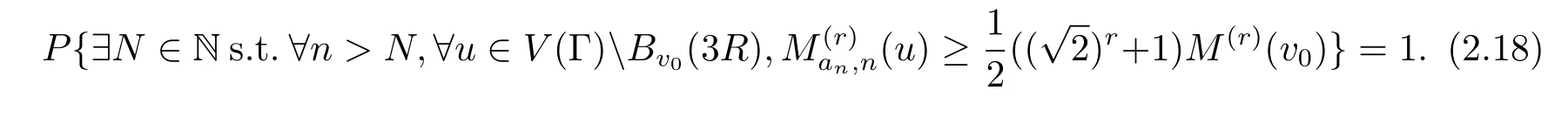
由引理2.4,∀v∈V(Γ)以及∀ε>0,有
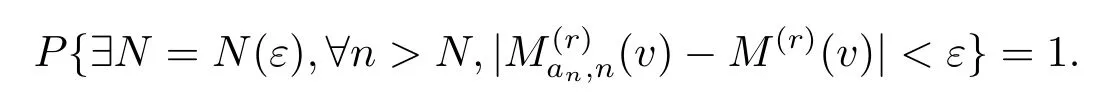
因为Bv0(3R)是有限集,可知上述收敛在Bv0(3R)上一致成立,即
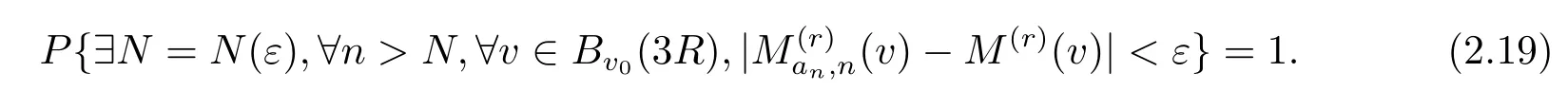
特别地,注意到E(ξ1)⊆Bv0(3R),取

最后,在(2.18)和(2.20)式给出的集合的交集上,由M(r)(v0)=M(r)(v)(因v0,v∈E(ξ1))以及(2.13)式,对满足条件的δ有
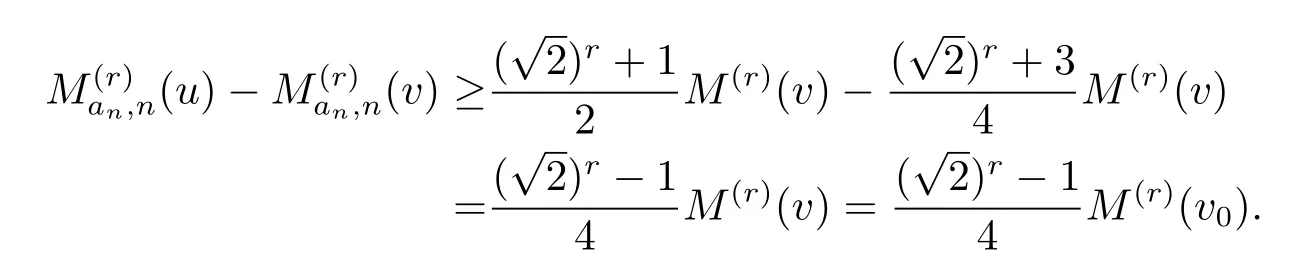
第二步,利用(2.15)式,取
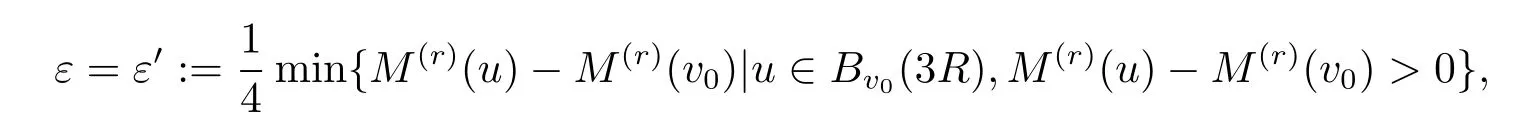
即以概率1,存在N=N(ε′)使得对∀n>N和u∈Bv0(3R),有ε′.由于E(ξ1)⊆Bv0(3R),因此,当v∈E(ξ1)时,有注意到M(r)(u)-M(r)(v0)>0,知存在N=N(ε′),使得当n>N时,∀u∈Bv0(3R)E(ξ1),有

且有
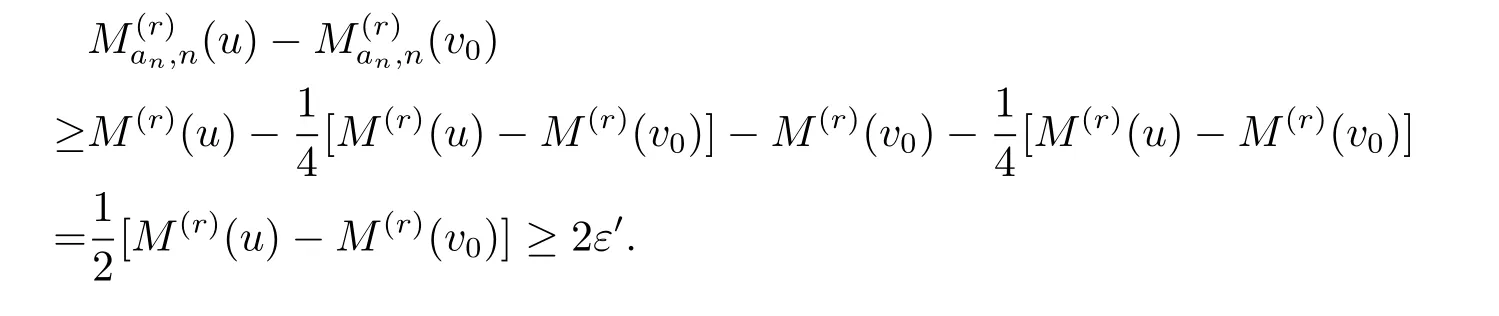
即
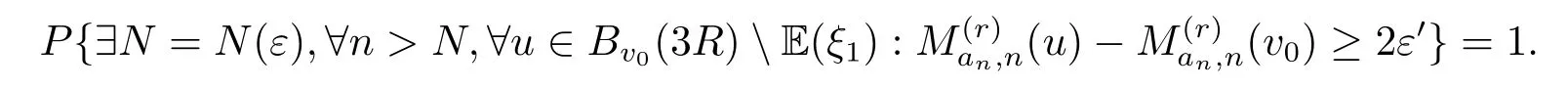
因此(2.14)式对δ≤2ε′成立.取δ=即可得引理成立.
3 强极限定理
经典的强大数定律表明,如果独立同分布随机变量的期望存在,则样本均值几乎处处收敛到随机变量的数学期望.然而,下面的例子可以看出,对在图上取值的随机元的广义样本均值在普通意义下并不一定收敛.
例3.1考虑图Γ=(V,E),其中V={v1,v2},E={(v1,v2)}.µ是由随机元ξ1:Ω→V诱导的V(Γ)上的概率测度,且此时有M(r)(v1)=M(r)(v2)=1/2, E(ξ)={v1,v2}.
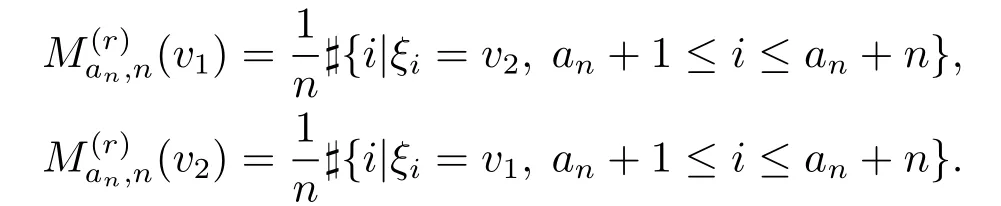
由定义2.3,有
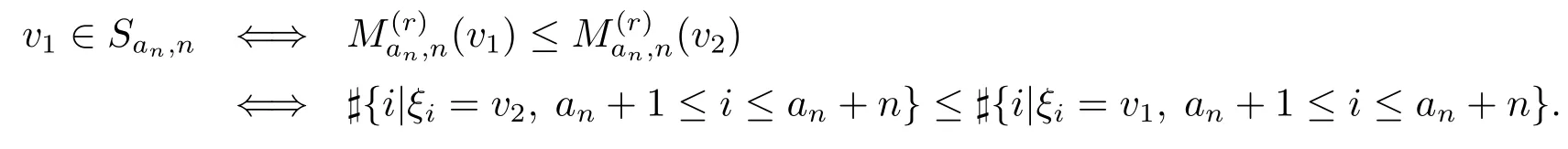
同理

令
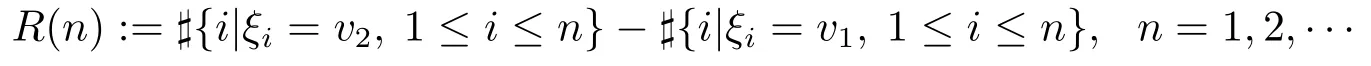
和
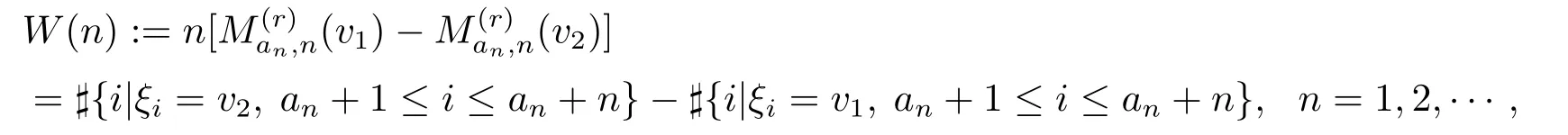
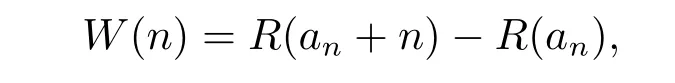
于是有

及
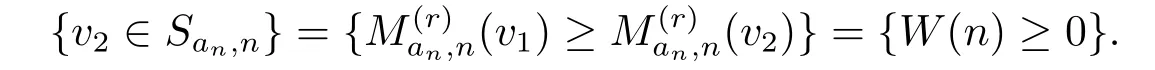
显然,W(n)与R(n)同分布.由于Z上的对称随机游动是常返的,从而有P{vi∈San,n,i.o.}= 1,i=1,2.因此

定理3.1设Γ是局部有限图,是定义在概率空间(Ω,F,P)上在V(Γ)中取值的一列i.i.d.随机元,µ是定义在Γ上由ξ1诱导出的概率测度.假设M(r)(u)<∞,∀u∈V(Γ).则
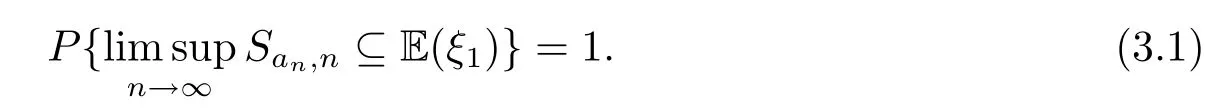
证由引理2.6,有
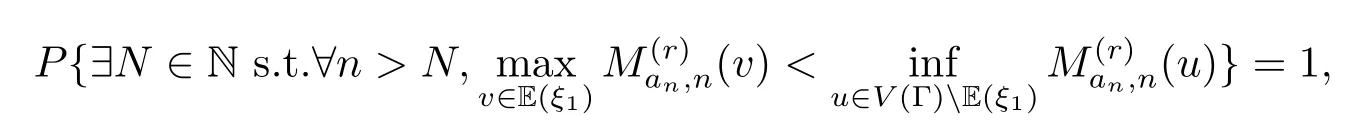
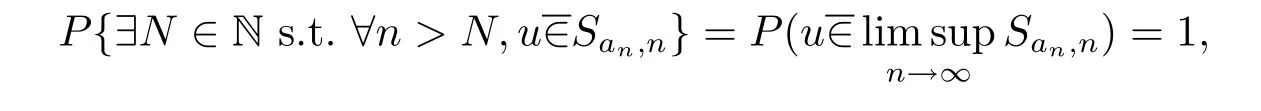
由测度的σ-可加性,有
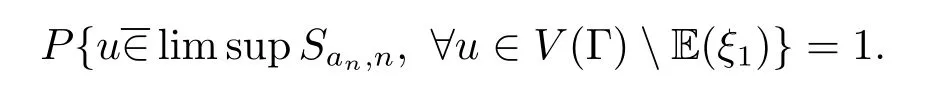
前面分别就Eξ1是单点与两点集这两种情况来证明强大数定理,关于Eξ1是多点集的情形的证明比较复杂,将在另文中讨论.
1.Eξ1是单点集情形.
定理3.2设Γ是局部有限连通图,是一列i.i.d.Γ-值随机元序列,ξi:Ω→V(Γ).如果<∞且E(ξ1)={v},v∈V(Γ),即E(ξ1)是单点集,则
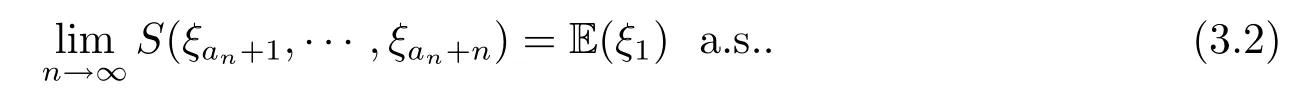
证(3.2)式可以表述为

或等价地
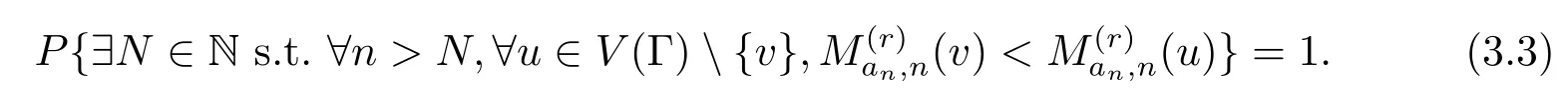
由引理2.6,有

于是
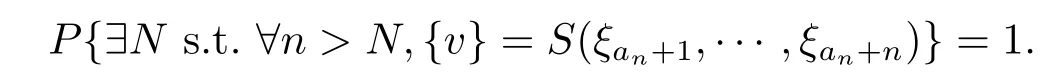
2.Eξ1是两点集的情形.
定理3.3设Γ是局部有限连通图,是一列i.i.d.Γ-值随机元,ξi:Ω→V(Γ).如果<∞且E(ξ1)={v1,v2},vi∈V(Γ),i=1,2,即#E(ξ1)=2,则
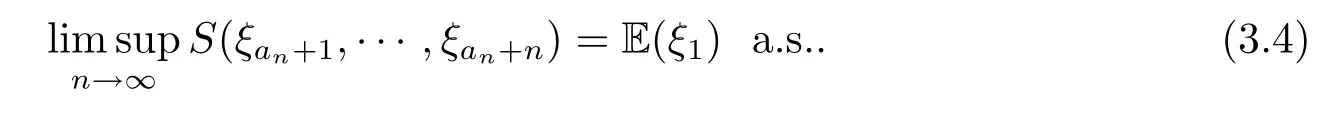
证由定理3.1知⊆E(ξ1).欲证(3.4)式,只须证明相反的包含关系.注意到E(ξ1)={v1,v2},即只在点v1和v2上取到最小值,即

由权函数的定义,有
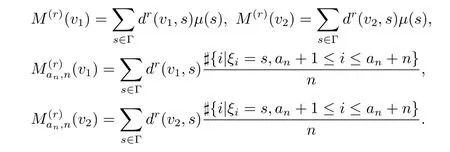
由引理2.4,有

由引理2.6知,存在数N∈N,当n>N,几乎处处有
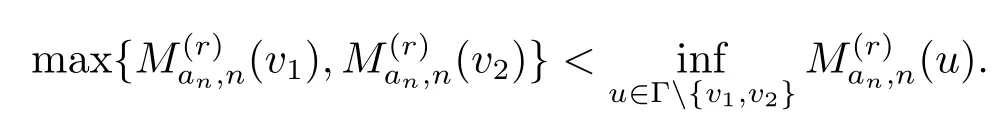
因此当n>N,

当且仅当

同理
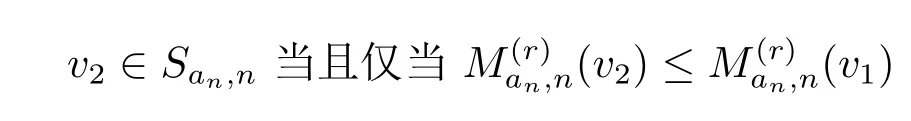
当且仅当
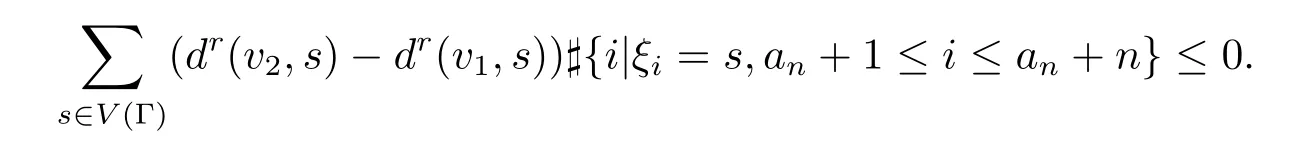
欲证{v1,v2}⊆只须证明无穷多次取正值和负值.令
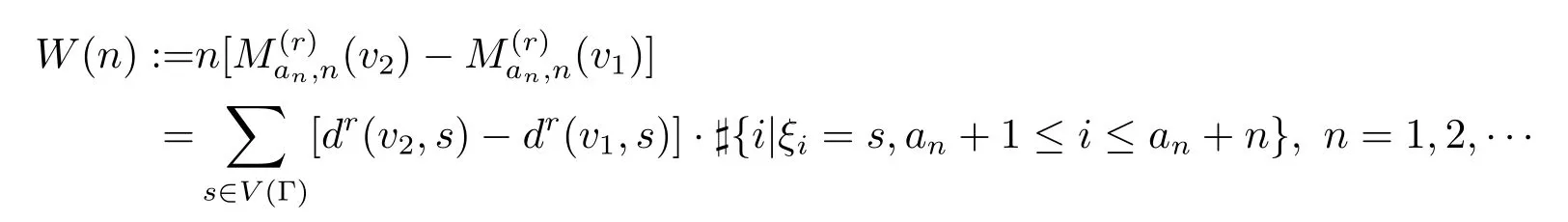
和
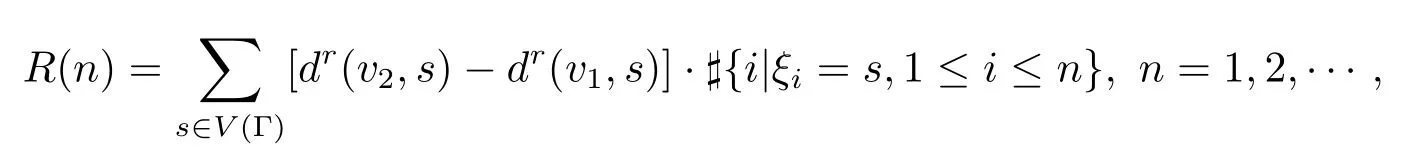
注意到,W(n)=R(an+n)-R(an)且W(n)与R(n)同分布,
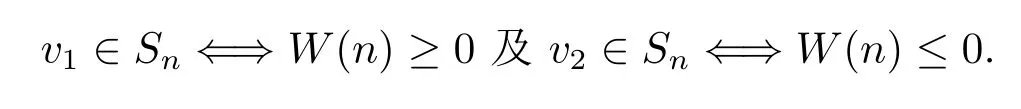
因为
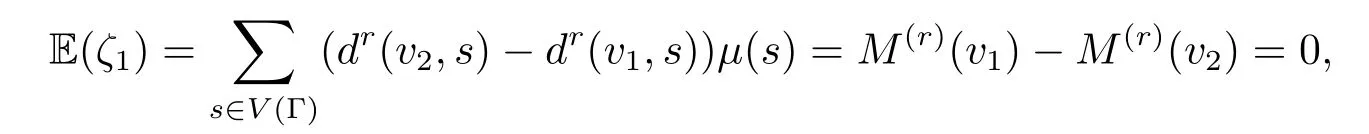
且

故
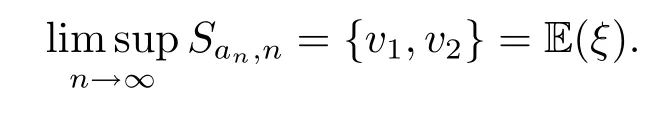
[1]Kolmogorov A N.La transformation de Laplace dans les espaces lineaires[J].CD.Acad.Sci.Paris, 1935,200:1717–1718.
[3]吴智泉,王向忱.巴氏空间上的概率论[M].吉林:吉林大学出版社,1990.
[4]Ziezold H.Expected figures and a strong law of large numbers for random elements in quasi-metric spaces[J].Trans.7th Prague Conf.Inf.Theory,Stat.Dec.Func.,Random Processes A,1977,591–602.
[5]Sverdrup H,Thygeson.Strong law of large numbers for measures of central tendency and dispersion of random variables in compact metric spaces[J].Ann.Stat.,1981,9:141–145.
[6]Bhattacharya R N,Patrangenaru V.Large sample theory of intrinsic and extrinsic sample means on manifolds-I[J].Ann.Stat.,2003,31:1–29.
[7]Mosina N,Ushakov A.Strong law of large numbers on graphs and groups[J].arXiv:0904.1005v2 [Math.PR]29 Jun 2010.
[8]Mosina N,Ushakov A.Mean set attack:cryptanalysis of Sibert et al.authentication protocol[J].J. Math.Crypt.,2010:4(2):149–174.
[9]Gaposhkin V F.The law of large numbers for moving averags of independent random variabls[J]. Math.Zametki,1987,42(1):124–131.
[10]Spitzer F.Priciples of random walk(2nd ed.)[M].New York,Berlin,Heidelberg:Springer-Verlag, 2001.
[11]Feller W.An Introduction to probability theory and its applications,Vol.II(2nd ed.)[M].New York: John Wiley,1971.
[12]张丽娜.任意B值随机变量的强收敛性[J].数学杂志,2002,22(3):297–300.
ON SOME LIMIT THEOREMS FOR GRAPH-VALUED RANDOM ELEMENTS
WANG Zhong-zhi,LI Wen-xi
(School of Mathematics&Physics Science and Engineering,Anhui University of Technology, Maanshan 243002,China)
In this paper,the authors discuss the basic properties of the general rth order mean set and rth order sample mean set of random elements,which take values on a locally connected graph,and the limit properties of them.By applying the separation lemma of random elements and the recurrence of random walk,we obtain the general strong law of large numbers for graph-valued random elements.Moreover,we generalize the existing results.
general strong law of large numbers;graph;r-th order weight function;r-th order mean set;r-th order sample mean set;random walk
tion:60F15
O211.4
A
0255-7797(2017)01-0118-11
2014-08-22接收日期:2015-03-19
国家自然科学基金(11071104);国家社会科学基金(13BJY011);安徽省自然科学基金(1308085QF113;1408085MA04);安徽工业大学研究生创新基金(2012090)资助.
汪忠志,男,安徽安庆,教授,主要研究方向:概率论及其应用.
猜你喜欢
杂志排行
数学杂志的其它文章
- INTERCHANGE BETWEEN WEAK ORLICE-HARDY SPACES WITH CONCAVE FUNCTIONS THROUGH MARTINGALE TRANSFORMS
- GLOBAL EXISTENCE AND BLOW-UP OF SOLUTIONS FOR NEWTONIAN FILTRATION EQUATIONS COUPLED WITH BOUNDARY CONDITIONS
- A MASCHKE TYPE THEOREM FOR PARTIAL π-COMODULES
- A NOTE ON HOMOGENIZATION OF THE HYPERBOLIC PROBLEMS WITH IMPERFECT INTERFACES
- OPTIMAL DIVIDEND STRATEGY IN THE BROWNIAN MOTION MODEL WITH INTEREST AND RANDOMIZED OBSERVATION TIME
- MAJORIZATION OF THE GENERALIZED MARTIN FUNCTIONS FOR THE STATIONARY SCHRDINGER OPERATOR AT INFINITY IN A CONE
