基于层次分析法与模糊数学的采矿方法优选

陶 明，罗福友

(江西国泰五洲爆破工程有限公司， 江西南昌 330038)

基于层次分析法与模糊数学的采矿方法优选

陶 明，罗福友

(江西国泰五洲爆破工程有限公司， 江西南昌 330038)

根据层次分析与模糊数学综合评价法，完成了采矿方法的选择，科学决策出千家坪钒矿最优采矿方法。在优选过程中，综合考虑影响采矿方案的各项指标，构造隶属度矩阵，并通过层次分析法对各指标进行权重计算和比较；根据模糊数学原理，建立模糊综合评价模型，综合各因素组合权重和隶属度矩阵得出3种采矿方法的最终评判向量B＝(0.9792，0.5058，0.2595)，合理优选出方案Ⅰ，即水平扇形深孔阶段矿房法为该矿最佳采矿方法。

采矿方案；层次分析；模糊数学；模糊综合评判

0 引 言

采矿方法的选择是否合理对矿山采切及回采工艺、回采效率、劳动生产率、采矿安全程度、矿石成本及矿山效益等产生重大影响，是否能正确选择合理的采矿方法关乎着矿山的命脉，因此科学合理的选择采矿方法是至关重要的。传统的做法是分别进行采矿方法初选、技术经济比较、综合技术经济比较进行选择[1]。但由于采矿方法选择受很多因素影响，难于确定各影响因素之间的关系，也无法解决各因素优越性交叉的问题。因此怎样衡量各个因素之间的相对权重关系是选择采矿方法的关键。以往的采矿选择方法要么无法处理多因素之间的权重关系，要么仅对单个因素进行分析，存在很大的片面性[2]。

随着近现代数学和计算科学的快速发展，层次分析法[3-4]、模糊数学[5]、灰色理论[6]、神经网络[7]等近现代数学理论被引入采矿方法的选择，取得了一定的成就。其中模糊数学可以将定性描述的指标进行无量纲化，从而进行模糊评价，但是模糊数学无法衡量多个因素之间的权重；层次分析法能建立将有关因素按不同属性分层的结构模型，并能科学合理的确定各个因素的权重。该文综合层次分析法与模糊数学原理，将其应用于采矿方法优选这一复杂的、多个影响因素的系统。

1 综合评判模型的构建

1.1 评价指标体系的的建立

首先建立因素集A＝{a1，a2，a3，a4，a5，…，an}，方案集X＝{方案1，方案2，方案3，…，方案n}，并构造相应的结构模型(见图1)，具有向下隶属性的方案影响因素作为准则层，而隶属于准则层的因素作为次准则层排在其下相应的位置，最顶端为目标层，即要优选出的最佳方案。

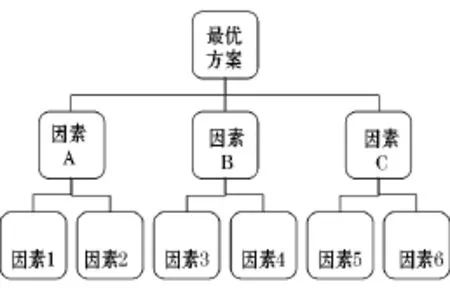
图1 层次结构模型

1.2 构造判断矩阵

从模型的第二层起，对隶属于上层同一元素的同层各因素相对重要性进行两两比较，如图1所示结构模型中，因素A、B、C需进行两两比较，隶属于A的因素1和2需进行比较等，比较直到最后一层，由此得到的矩阵称为判断矩阵[8]。比较同一层各因素有关上一层对应因素的相对重要性时，使用数值对权重来描述，aij的取值在1～9之间，它的赋值可参考表1[9]。

其中对比矩阵(判断矩阵)表达式为:

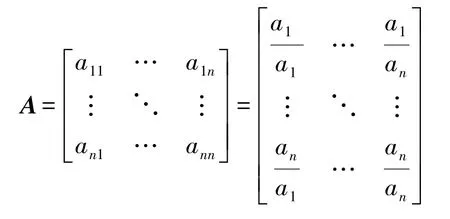
表1 判断矩阵标度值及含义

1.3 计算权向量并做一致性检验

从理论上分析，如果判断矩阵满足完全一致性，则有aijajk＝aik，aij＞0，aii＝1，aji＝1/aji成立。但实际上，由于事物的复杂性和不确定性，矩阵完全满足上述条件是不可能的，因而只要求判断矩阵在一定程度上满足一致性，也就是满足上述部分条件。利用Matlab软件计算各判断矩阵的权值向量，并检验一致性，若不通过，需重新构造判断矩阵，直到检验通过为止。检验步骤如下:

(1)计算不一致程度的指标CI:

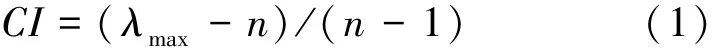
式中，λmax为矩阵最大特征值

(2)查看矩阵一致性标准RI:RI是平均随机一致性指标，它的大小只与矩阵维数有关，RI的取值见表2。

表2 平均随机一致性指标取值

(3)计算随机一致性比率CR:

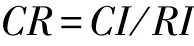
判断方法:当CR＜0.1时，认为判断矩阵具有满意的一致性，否则调整矩阵A直到满足上式。

根据以上所求每个判断矩阵的权向量确定因素a1，a2，…，an相对于目标层的权向量(组合向量)，构造层次总排序表，并检验一致性，若不通过，重新构造判断矩阵或调整一致性比率较大的判断矩阵，直到一致性满足条件为止。

1.4 隶属度矩阵的建立

由于不同指标单位不同，没有可比性，需进行无量纲化，因此必须构造隶属度矩阵，其中定量指标的隶属度由隶属函数确定，定性指标可通过相对二元比较法进行确定。

(1)定量指标。定量指标可分为2种:收益性指标，对于收益性指标，越大越好，以式(2)作为隶属度函数；消耗性指标，对于消耗性指标，越小越好，以式(3)作为隶属度函数[10]。

xij为收益性指标时:

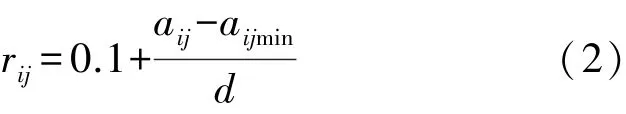
xij为消耗性性指标时:

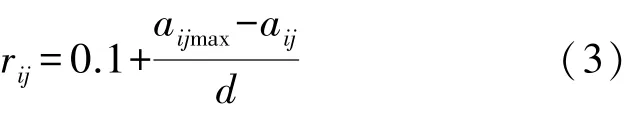
式中，aij为j方案i指标的评判；aimin为i指标的下限值；ximax为i指标的上限值；d为极差，d＝(ximaxximin)/(1-0.1)。

(2)非定量指标。设有非定量因素集X＝{X1，X2，X3，…，Xn}，利用二元比较法对各因素进行重要性比较，并进行相应排序，得到的二元比较矩阵E如式(4)，其中ekl的值由因素集中Xl与Xk的重要性决定，其取值如表3所示[11-12]。

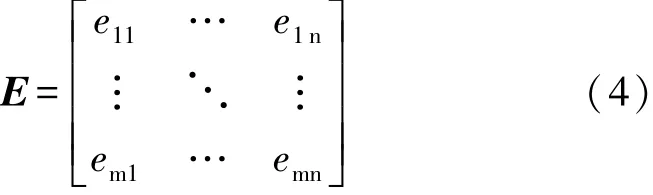
表3ekl的取值

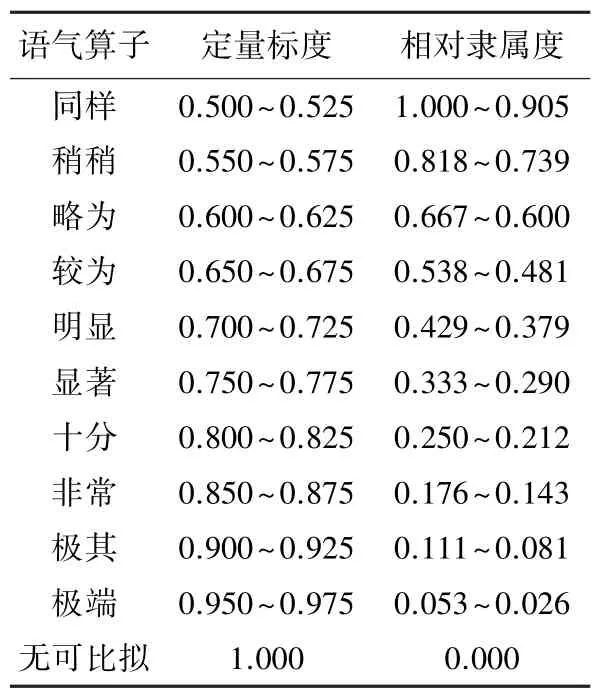
表4 语气算子与定量标度相对隶属度关系表

1.5 综合评判

由上文所求组合权向量W(归一化)及隶属度矩阵R确定综合评判向量B。

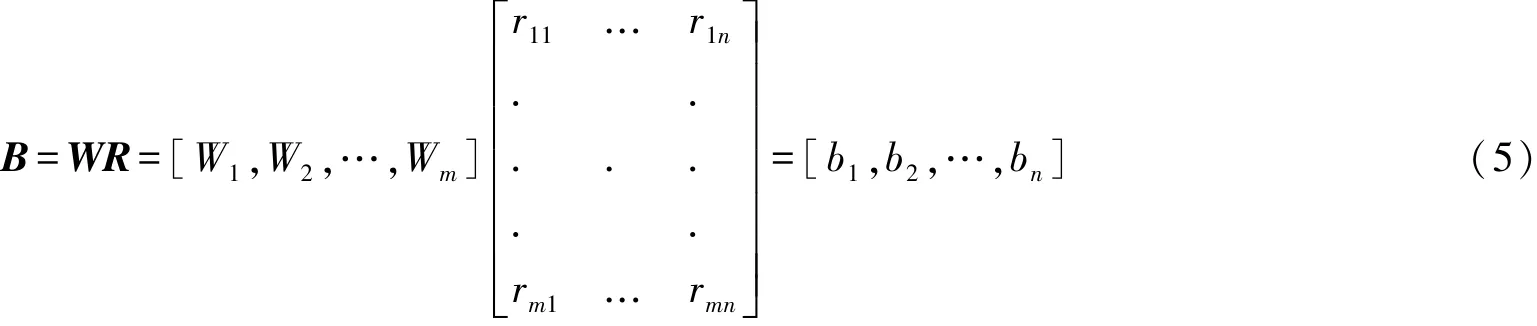
式中，bi为方案X的综合优越度。

2 工程实例应用

某矿山矿体呈层状结构，矿体厚11 m，矿体倾角60°～75°，开采技术条件一般，矿床为石英脉型，钨矿为黑钨矿石，矿脉延伸较长，属于急倾斜薄矿脉，脉群之间相邻矿脉间距一般达1～10 m，有的多达几十米，矿脉形态变化稳定且脉幅较为均匀，围岩主要为变质砂岩，矿岩是石英岩伴生，围岩岩性主要表现出坚硬至半坚硬，普氏系数8～12左右，因该矿山采矿作业正处于初期，暂时未形成统一的采矿方法，经过对矿山前期现场安全及生产情况分析，并结合理论综合分析，初选出水平扇形深孔阶段矿房法、分段空场采矿法和无底柱分段崩落法3种采矿方法，为提高采矿效益，保证采矿安全，需优选出最佳采矿方法。

2.1 评价指标体系

本次分析影响因素诸多，根据《采矿手册》并结合采矿现场经验，仅以9个因素作为评价指标，技术指标为出矿工效，凿岩工效，采切比，矿石回收率，矿石贫化率，炸药单耗，工艺过程的复杂程度；经济指标为采矿直接成本；安全指标为方案的安全程度。

确定因素集{a1，a2，a3，a4，a5，a6，a7，a8，a9}＝{出矿工效，凿岩工效，采切比，矿石回收率，贫化率，炸药单耗，工艺过程的复杂程度，采矿直接成本，方案的安全程度}。

根据前文分析，以3个方案为评价对象，即X＝{X1，X2，X3}＝{方案Ⅰ，方案Ⅱ，方案Ⅲ}。

2.2 判断矩阵及指标权重的确定

构建一级指标层(准则层)对应于目标层的判断矩阵(见表5)，其中CR＝0.0462＜0.1，检验通过。构建二级指标层(子准则层)对应于一级指标层的判断矩阵(见表6)，其中CR＝0.00572＜0.1，检验通过。

综合各单排序表，计算各因素的组合权重，见表7。根据表7，CR＜0.1，检验通过。

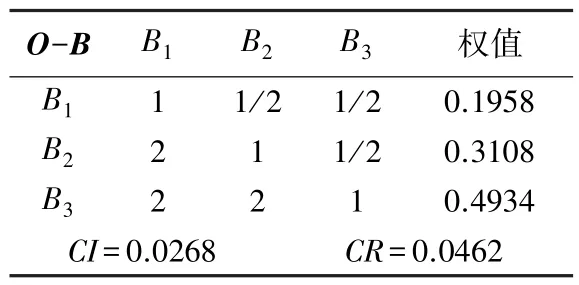
表5O－B判断矩阵

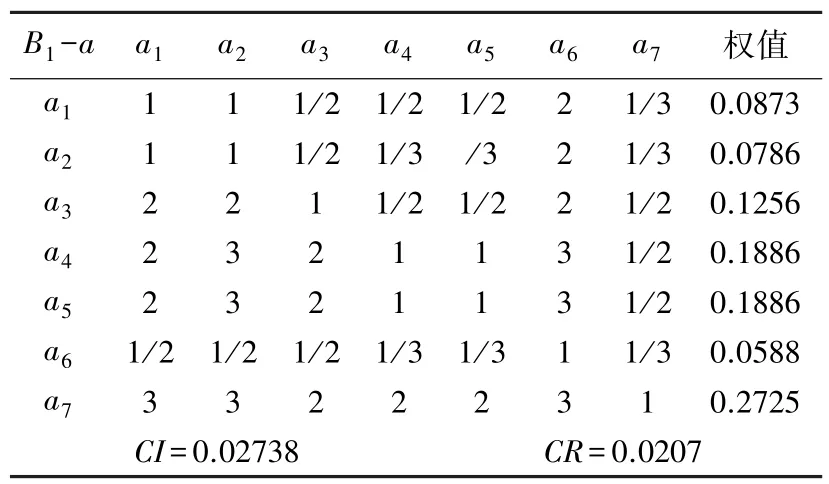
表6B1－a判断矩阵

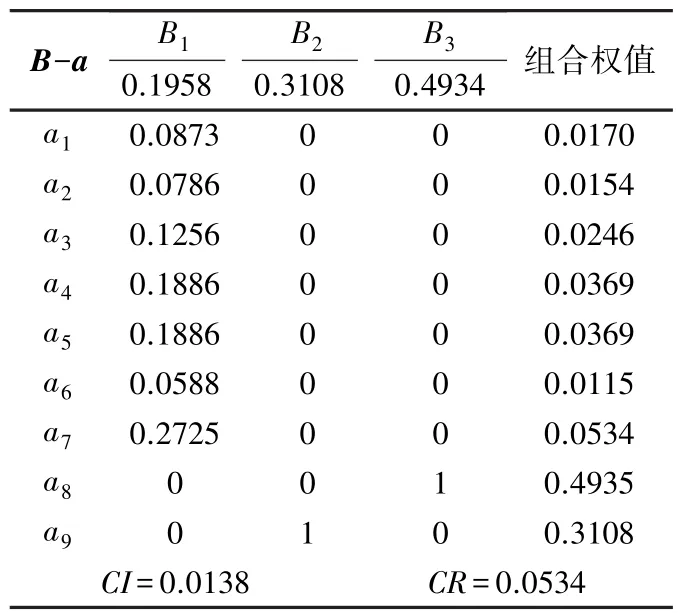
表7 各因素权重

2.3 构造隶属度矩阵

(1)3个采矿方案的综合评价指标见表8，根据收益性与消耗性定量指标的隶属度计算函数，得出7个定量指标的隶属度矩阵:

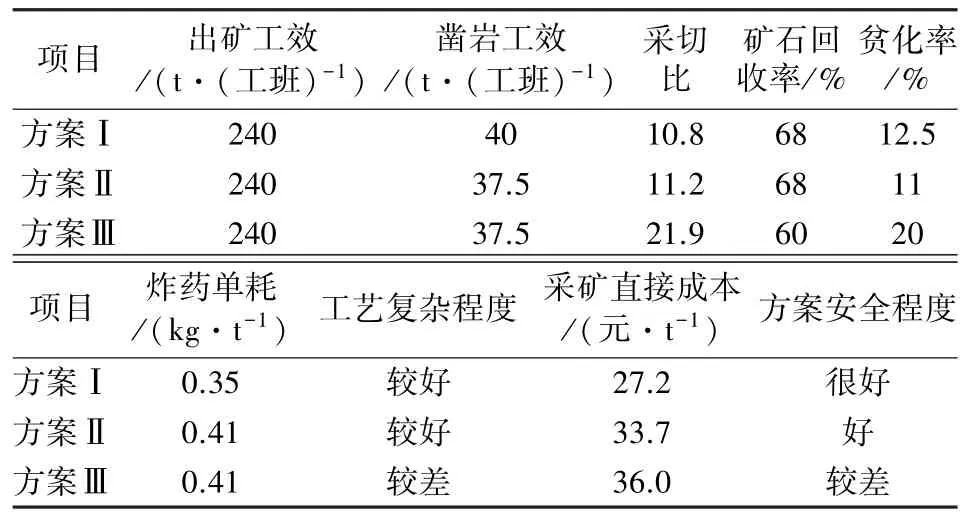
表8 综合评价指标

规格化特征向量矩阵得:

比较各方案的工艺复杂程度，可得特征向量矩阵:

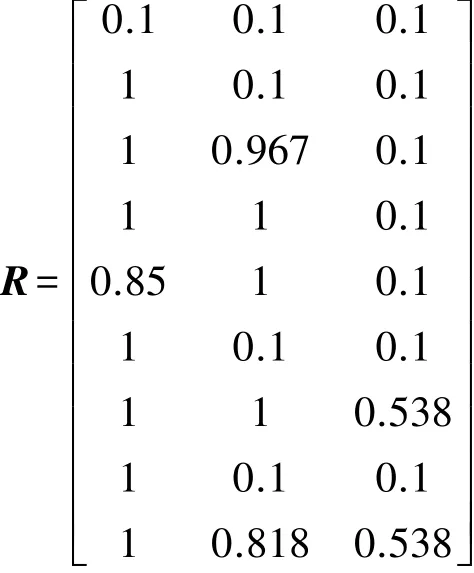
则隶属度矩阵R7＝[1 1 0.538]。

比较各方案的安全程度，可得特征向量矩阵:

则隶属度矩阵R9＝[1 0.818 0.538]。

综上所述得总的隶属度矩阵:

2.4 综合评判

综合以上计算出的权重向量W及隶属度矩阵R可得出综合评判向量B:

B＝W·R＝(0.9792，0.5058，0.2595)，由此可得3种方案的优劣次序:方案Ⅰ→方案Ⅱ→方案Ⅲ，方案Ⅰ最优，即水平扇形深孔阶段矿房法为该矿最佳采矿方法。

3 结 论

(1)利用层次分析法分配各因素权重，并结合矿山实例，根据模糊数学原理建立模糊评价模型，最终通过层次分析与模糊数学综合法得出各方案优越度为0.9792，0.5058，0.2595，即方案Ⅰ为最佳方案。

(2)层次分析与模糊数学综合法是一种科学合理的分析方法，该方法首先通过层次分析法确定各个因素之间的权重，避免了各方案多个影响因素优越性交叉，解决了多个影响因素而难于确定权重的难题；其次根据模糊数学原理确定隶属度矩阵，建立模糊评价模型，避免了人们因主观认识而产生的弊端。

[1]刘华生，王洪海.层次分析在采矿方法选择中的应用[J].有色金属，1991，43(3):17-21.

[2]王新民，赵 彬，张钦礼.基于层次分析和模糊数学的采矿方法选择[J].中南大学学报(自然科学版)，2008，39(5):875-880.

[3]杨 扬，冯乃琦，余珍友，等.基于层次分析和模糊数学的采空区稳定性综合评价[J].有色金属(矿山部分)，2008，60 (5):37-39，42.

[4]刘玉龙，丁德馨，李广悦，等.层次分析法在铀矿山采矿方法优化选择中的应用[J].矿业研究与开发，2011，31(6):8-10，112.

[5]肖木恩.模糊数学在采矿方法选择中的应用[J].矿业研究与开发，2003，23(01):15-17.

[6]Liu zhi-xiang，etc.Laws of strata energy release and corresponding safety warning system in metal mine[J].Transactions of Nonferrous Metals Society of China，2011，21(11):2508-2512.

[7]陈建宏，刘 浪，周智勇，等.基于主成分分析与神经网络的采矿方法优选[J].中南大学学报(自然科学版)，2010，41 (5):1967-1972.

[8]张永达，明世祥，明 建，等.模糊聚类及层次分析法在采矿方案优选中的应用[J].矿业研究与开发，2015，35(06):1-4.

[9]高 阳，余建伟.判断矩阵标度扩展法在不同标度下的比较[J].统计与决策，2007(20):152-154.

[10]邓 飞，胡龙飞，朱 明，等.千家坪钒矿采矿方法优化研究[J].中国矿业，2014(02):96-101.

[11]徐 飞，褚洪涛，刘晓亮.基于模糊评判的杨家湾铁锌矿开采方案优选[J].采矿技术，2013，13(01):4-5，32.

[12]柳小胜.基于粗糙模糊集理论的采矿方法优选[J].采矿技术，2008，8(04):1-3.

2015-12-17)