鱼眼图像径向畸变校正的一种新方法

师 平

(江苏航空职业技术学院，江苏 镇江 212134)

鱼眼图像径向畸变校正的一种新方法

师 平

(江苏航空职业技术学院，江苏 镇江 212134)

由于鱼眼相机视场广阔在很多领域都得到了广泛应用，但其图像存在着明显的径向畸变，需要在应用之前加以校正。为此分析了径向畸变模型解析解的非唯一性；根据径向畸变的对称性，得出了畸变直线与理想直线之间的关系，即畸变校正的解析表达式；提出了一种鱼眼图像径向畸变校正的新方法。实验证明，该方法计算简单，能有效校正包含直线特征的场景。

径向畸变；鱼眼图像；几何校正；畸变校正

鱼眼镜头因其宽视场的特点广泛应用于区域监控、机器导航和智能交通等领域。但是鱼眼镜头拍摄的图像存在较大程度的失真，为了后续处理的方便，必须对失真图像进行处理，即畸变图像校正[1]。目前，畸变图像校正大体可分为2种途径：①将畸变模型代入小孔成像模型中，然后通过标定摄像机的内外参数求出的畸变模型将图像校正，常见的标定方法有基于特征点的标定[2]、基于相机扭曲系数的标定[3]。②不标定摄像机内外参数，仅利用单幅图像的几何特征建立统一的畸变模型，再通过数值方法优化出最优解进行校正，常见的方法有根据畸变曲线的弯曲特点[4]、用椭球面模型[5]、球面坐标投影模型[6]和弧面映射模型[7]等去逼近和拟合；还有利用直线畸变后形成的曲线的圆心共线约束[8]、利用直线畸变特征[9]和利用直线投影几何不变性[10]等许多思路。文献[11]提出了一种不预先设定模型，通过像点之间的约束来解算模型的新算法。文献[12]提出了畸变能量的定义方法，可用于评价畸变的程度。该方法的优势在于不设定畸变模型首先减少了模型误差对标定的影响。

本文通过分析径向畸变的对称性，得出畸变曲线与理想直线之间的关系，即曲线畸变校正的解析表达式；进而提出一种基于径向畸变模型的几何校正方法。采用鱼眼图像进行实验，对不同阶次的模型进行对比。

1 径向畸变模型

畸变可分为径向畸变和切向畸变，由于切向畸变较小，本文仅对径向畸变进行建模。径向畸变根据镜头的不同可以大致分为桶形畸变和枕形畸变两种[13]。一般来说，径向畸变模型可以表述为[14]

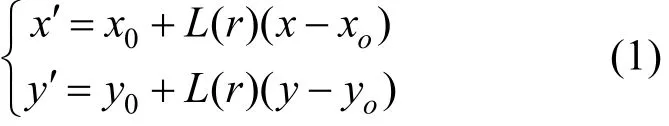
如列向量 (x, y,1)T为图像点 P测量的坐标，(x', y',1)T为矫正后的理想像点 P'的坐标，而(x,y ,1)T为径向失真中心P0的坐标，r为实际像oo点到径向失真中心的距离，即。L(r)是径向失真因子，仅是半径r的函数。

其中，只有 r为已知量，r'与 L（ r）均是未知的，对于一个多元方程，其解析解并不是唯一的。下面通过分析将说明径向畸变模型的最优解是一组线性相关的解。

假设物点 Pi在摄像机坐标系下的坐标为(Xi, Yi, Zi)，其对应的实际像点为 pi( xi, yi)，采用基于重投影最小准则的标定方法，得到畸变因子为L( ri)，焦距为f。证明畸变因子 L'( ri) = L( ri)×λ，焦距f'=f×λ，也可以使重投影达到最小。

重投影公式为

其中，内参数(f, L( r))与(f',L'( r))在代数上等价，都可以使重投影最小，说明其解都是最优解，即径向畸变模型的最优解是一组线性相关的解。

因此，本文用的径向畸变模型有不唯一的解析解，其数值最优解是一组线性相关的解。

2 径向畸变模型的对称性分析

2.1 畸变的对称性

根据式(2)，发现当实际像点矢径 r相同时，其畸变量也是一致的，即与主点距离相同的点其畸变量也相同，称这种规律为畸变的对称性，用公式表述则为：

(1) 主点距离相同的 2个像点为 P1( x1, y1)、P2( x2,y2)，即

此规律体现了畸变图像中各像点之间的联系与制约关系，且直线畸变后形成的曲线也不是相互独立的，下面探讨畸变直线之间的量化关系，进而据此得出畸变曲线对应的理想直线的参数。

2.2 畸变曲线校正

假设像点P1、P2分别在畸变曲线C1、C2上，其对应的理想直线分别用列向量表示为 l1T=(a1, b1,1)， l2T=(a2, b2,1)，则有分别在l1、l2，即

将式(4)～(7)转化为代数表达式则为

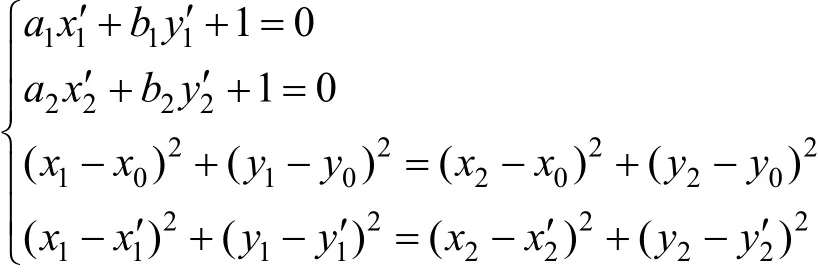
经过整理得

当取主点为原点，则有

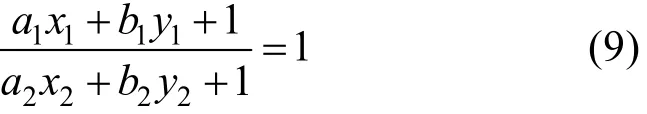
根据式(9)，可以得出以下2个结论：

结论1. 当l1=l2时，

利用该结论，可以直接求解出畸变曲线对应的理想直线的斜率。

利用该结论可以进一步求解出两条理想直线第2个参数之间的关系。

至此可以得出畸变点和理想直线参数之间的关系，只要找到主点，就可以直接求出畸变曲线对应的理想直线的参数。

3 畸变校正算法

到主点就可以找到畸变曲线和理想直线之间的关系，即可以将畸变曲线还原为其本来的理想直线，进而可以求出畸变模型。具体的畸变校正算法流程如图1所示。

3.1 主点拟合

拟合主点的方式有很多，本文采用畸变曲线对称轴交汇的方法进行求解，具体方法见图2。

图2中，P0为畸变中心；曲线C1、C2为直线畸变后形成的曲线；T1、T2为曲线C1、C2上部分点拟合形成的二次曲线。根据畸变对称性原理，畸变曲线是轴对称图形，并且主点必过对称轴，则有二次曲线对称轴就是畸变曲线的对称轴，多条对称轴的交点即为主点。

3.2 直线参数求解

如图3所示，以曲线C1为例，说明其理想直线的参数求解过程，以 P0( x0,y0)为圆心，以rk1为半径做圆交曲线C1于 (xk11,yk11)、( xk12,yk12)两点，根据式(9)，则有

依照此方法，可以求出 k2, k3,… ,kn等。

根据2.2节的结论2求解直线的第2个参数。假设b1=1(根据第一节证明的径向畸变模型的解不唯一性，这样的假设是有效的)，以 (x0,y0)为圆心，以rb1为半径做圆交曲线C1、C2于 (xb11,yb11)、(xb12,yb12)两点以此方法，可以依次求出 b2, b3,…,bn等。

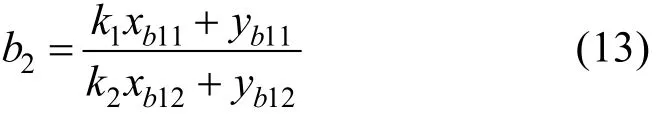
3.3 求解畸变模型

同文献[15]所提方法类似，根据理想直线和畸变曲线的对应关系，可以计算得出一组点的矢径r1, r2,… ,rn，对应的理想像点的矢径 r1', r2' ,… ,rn' ，然后可以选择模型去拟合畸变因子函数L( r)。本文选择多项式模型进行拟合，模型的阶次需要根据校正效果进行选择，即参数 n是一个经验值，需要通过实验进行设置。事实上，本文通过实验证明，取 n=3时，校正的效果就已经不错了。进一步提高阶数，大大增加了计算量，效果改善却并不明显。

得到畸变模型后，畸变校正就是畸变模型的反变换。利用式(1)，根据拟合模型求得的最优模型可以将原图像上的像素点进行映射，即可得到校正后的图像。

4 实验与分析

本文实验采用鱼眼镜头实际拍摄棋盘格图像，图像大小为720×480。如图4所示，任意选取6条直线，在每条直线上选取15个点，根据式(11)拟合出各条直线，对应如下式的二次曲线

进一步根据该二次曲线的对称轴求其交点，可以得出主点坐标为(340.0868 202.6049)。据式(12)和(13)，求出6条直线的2个参数如表1所示。

图4 鱼眼镜头畸变后的图像

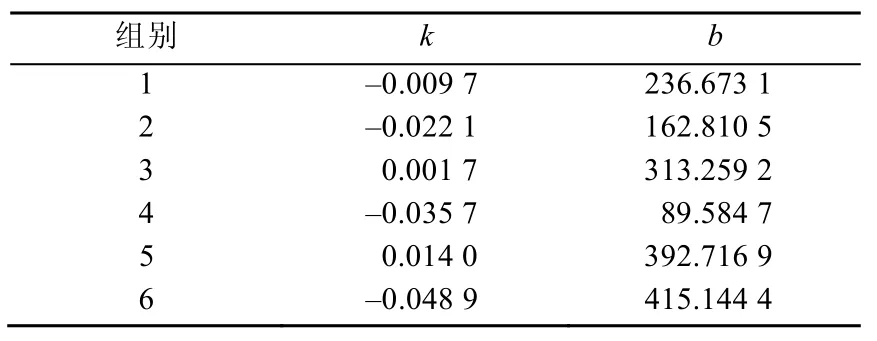
表1 拟合直线参数表

在求得的主点坐标和理想直线的基础上，可以用畸变因子表征直线不同位置点的畸变程度，即不同矢径对应不同的畸变因子，其关系可用图5所示。其中横坐标为径矢r，单位为像素；纵坐标为畸变因子，单位是无量纲。

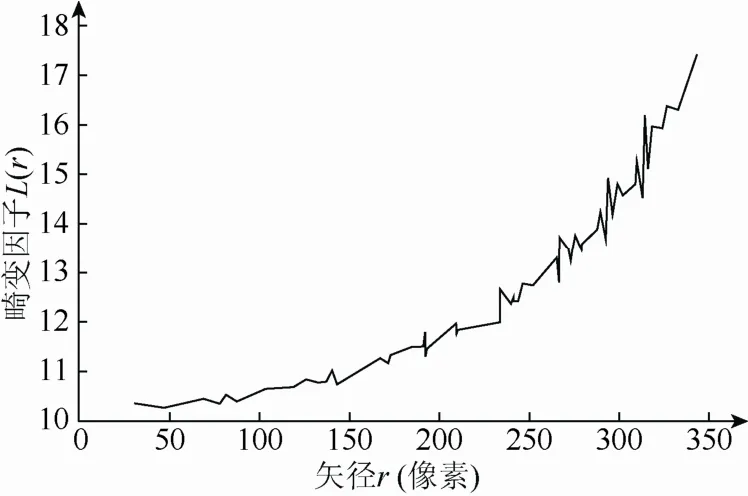
图5 矢径与畸变因子对应的关系图

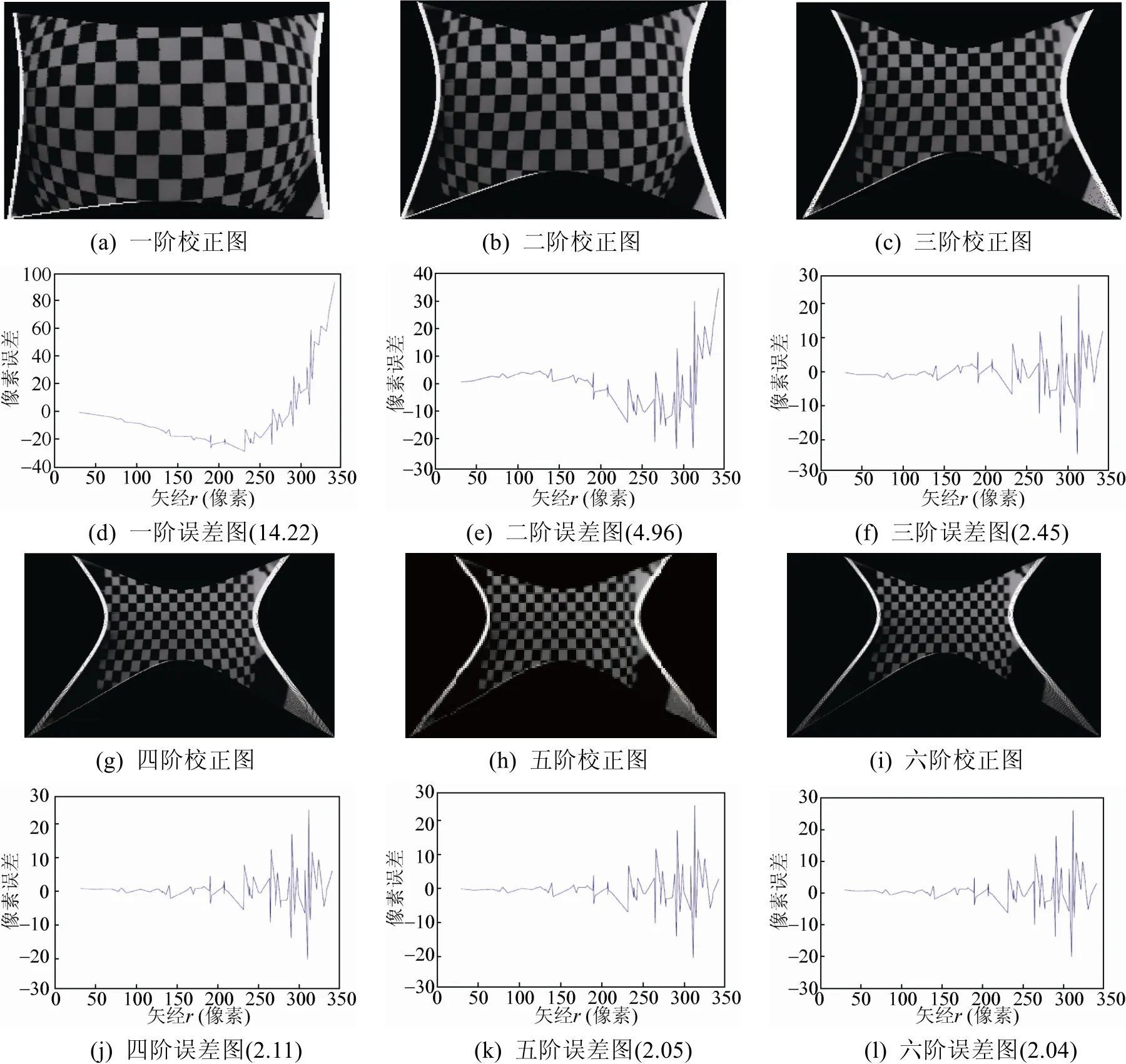
图6 各阶畸变误差及校正图

如图 6所示，采用一、二阶模型时，校正误差较大，三阶以上误差变化不明显。而三阶模型的计算量更少，因此畸变模型一般采用三阶就可以了。

与文献[13]相比，本文方法计算简单，原理清晰，可以用较少的数据量得到比较精确的结果。

5 结论与展望

随着鱼眼相机的广泛应用，鱼眼图几何畸变校正已经成为当前重要的研究热点。本文研究了径向畸变模型，证明其解析解不唯一，且最优解是一组线性相关的解；分析了径向畸变的对称性，得出畸变曲线与理想直线之间的关系，即曲线畸变校正的解析表达式；提出了一种基于径向畸变模型的几何校正方法。实验证明，该方法计算简单，能有效校正包含直线特征的场景。且对于该模型，并不是阶次越高越好：三阶以前拟合误差随着阶次的升高而降低，三阶以后下降的不太明显。因此，通常选择三阶模型。

下一步工作主要关注 2个方面：①多项式拟合中存在龙格现象，文章没有考虑；②畸变模型中没有考虑切向畸变。

[1] Faisal B, Matthew N. Automatic radial distortion estimation from a single image [J]. Journal of Mathematical Imaging and Vision, 2013, 25(1): 31-45.

[2] 刘 艳, 李腾飞. 对张正友相机标定法的改进研究[J].光学技术, 2014, 40(6): 565-570.

[3] 黄 淼, 周志光, 陶煜波, 等. 基于数码相机参数还原的多屏拼接几何校正技术[J]. 计算机辅助设计与图形学学报, 2010, 22(10): 1803-1809.

[4] Dunne A K, Mallon J, Whelan P F. Efficient generic calibration method for general cameras with single centre of projection [C]//IEEE 11th International Conference on Computer Vision. New York: IEEE Press, 2007: 1-8.

[5] 杨中伟, 杨 鸣. 基于椭球面模型的鱼眼图像校正方法[J]. 光学仪器, 2015, 37(2): 127-131.

[6] Xiao S Z, Wang F W. Generation of panoramic view from 360 degree fisheye images based on angular fisheye projection [C/OL]//Distributed Computing and Applications to Business, Engineering and Science (DCABES), 2011 Tenth International Symposium on. [2015-08-10]. https://www.computer.org/csdl/proceedings/ dcabes/2011/4415/00/4415a187.pdf.

[7] Formea R T, Tahri O, Chaumette F. Distance-based and orientation-based visual servoing from three points [J]. IEEE Transactions on Robotics, 2011, 27(2): 256-267.

[8] 朱云芳, 杜 歆. 基于圆心共线约束的鱼眼镜头径向畸变估计[J]. 光电工程, 2014, 41(11): 36-43.

[9] Ricardo G, Agustin O, Ricaro F, et al. Uncertainty analysis of the DLT-Lines calibration algorithm for cameras with radial distortion [J]. Computer Vision and Image Understanding, 2015, 40(3): 115-126.

[10] 傅 丹, 周 剑, 邱志强, 等. 基于直线的几何不变性标定摄像机参数[J]. 中国图象图形学报, 2009, 14(6): 1058-1063.

[11] Hartley R I, Kang S B. Parameter-free radial distortion correction with centre of distortion estimation [J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2007, 29(8): 1309-1321.

[12] Shi J, Zhao X Y, Zhang C M, et al. An evaluation method for distortion energy parameterization of triangular meshes [J]. Computer Aided Drafting, Design and Manufacturing, 2013, 23(3): 13-17.

[13] Zuzana K, Martin B, Klas J. et al. Fast and robust numerical solutions to minimal problems for cameras with radial distortion [J]. Computer Vision and Image Understanding, 2010, 114(2): 234-244.

[14] Wu Y H, Hu Z Y, Li Y F. Radial distortion invariants and lens evaluation under a single-optical-axis omnidirectional camera [J]. Computer Vision and Image Understanding, 2014, 126(9): 11-27.

[15] 张海彬, 余 烨, 李 琳, 等. 基于视点纠正的鱼眼图像场景化漫游方法[J]. 图学学报, 2014, 35(3): 435-441.

A Novel Method for Fish-Eye Image Radial Distortion Correction

Shi Ping
(Jiangsu Aviation Technical College, Zhen jiang Jiangsu 212134, China)

Since the fish-eye camera has wide view field, it has been used widely in many fields. However, there is seriously radial distortion, needed to be corrected before any application. Fish-eye image geometric correction is a hot and difficult problem in current industrial applications and theoretical research. This paper presents a radial distortion model, and point out its analytical solution is not unique. According the symmetry of the radial distortion, reveals the relationship between a distortion curve and its ideal straight line, called the analytical expression of the curve distortion correction. Based on the previous analysis, this paper proposes a geometric correction method. Experiments show that this method is simple, can effectively corrects the scene which containing line features.

radial distortion; fish-eye image; geometric correction; distortion correction

TP 37

10.11996/JG.j.2095-302X.2016060805

A

2095-302X(2016)06-0805-05

2016-05-09；定稿日期：2016-05-29

师 平(1969-)，男，江苏镇江人，副教授，硕士。主要研究方向为智能制造。E-mail：zj2119663@126.com