希尔伯特-黄变换在微弱被动瞬态鱼声信号中的检测

2017-01-18王平波鲍玉军许清泉陈宗涛

海洋科学 2016年10期

陈功, 王平波, 鲍玉军, 许清泉, 杨辉, 陈宗涛

陈功1, 2, 王平波3, 鲍玉军1, 许清泉1, 杨辉1, 陈宗涛1

(1. 常州工学院, 江苏常州 213022; 2. 厦门大学, 福建厦门 361005; 3. 海军工程大学, 湖北武汉 430033)

为了在海洋环境中准确获取鱼类在摄食、产卵和争斗过程中发出的短促、瞬时的信号, 采用希尔伯特-黄变换算法实现微弱被动瞬态鱼声信号的检测。该算法首先将瞬态鱼声信号实现固有模态信号的分解, 其次将经验值高阶阶数的固有模态信号求和重构即可实现信号能量幅度检测; 在固有模态信号的分解的基础上, 计算求和重构信号的希尔伯特能量谱, 即可实现瞬时能量密度级的检测。通过不同信噪比和检测器的比较研究, 结果表明基于希尔伯特-黄变换算法的两种检测方法能有效提高微弱被动瞬态鱼声信号的检测性能。

被动瞬态鱼声; 希尔伯特-黄变换; 信噪比; 检测器

鱼类在水下环境中发出的噪声可以分为两种, 一种是在交配季节连续性重复地发出的求偶声信号, 另一种是在摄食、产卵和争斗过程中, 所发出的短促、瞬态的被动鱼声信号。连续发出的鱼声信号可以采用常规的信号处理方法用于检测和识别, 这些信号处理技术通常包括带通滤波技术、时频变换以及混合神经网络算法[1-9]。由于瞬态信号维持时间短, 一般都在毫秒级, 产生频率较少, 时域中通常表现为一两个尖刺, 且不具备重复性, 如果信噪比太小的话很难从被测信号中直接检测; 此外海洋背景比较复杂, 环境噪声影响严重, 因此被动瞬态鱼声信号的检测比较困难。考虑到信号频率成分多样且时变, 不适用于传统的傅里叶变换方法; 而短时傅里叶变换、Wignner-Ville分布和小波变换可用于处理瞬态信号, 其中短时傅里叶变换适合研究平稳信号, 而瞬态信号具有强烈的非平稳性且频率变换快, 因此该方法不可能在时、频域同时获得较高分辨率。Wignner-Ville分布在分析瞬时信号时会产生“交叉项”[10]。小波变换在处理非平稳信号领域具有优越性, 但分析结果取决于小波基函数的选取。

希尔伯特-黄变换(Hilbert-Huang Transform, HHT)[11-12]适合处理非平稳、非线性信号, 其不受傅立叶分析的局限, 能够精确地表达信号的时域和频域分布, 是一种更具有自适应性的时频局部分析方法。本文利用HHT的滤波特性, 提出了一种基于HHT信号重构思想的被动瞬态鱼声信号检测方法。该算法首先将瞬态鱼声信号实现固有模态信号的分解, 其次将经验值高阶阶数的固有模态信号求和重构即可实现信号能量幅度检测; 在固有模态信号的分解的基础上, 计算求和重构信号的希尔伯特能量谱, 实现瞬时能量密度级的检测。

实验结果表明, 基于信号重构的信号瞬态能量幅度检测方法, 提高了信号的信噪比、检测概率和准确度, 说明基于 Hilbert 黄变换经验模态分解的瞬态信号检测性能优于传统能量检测算法; 采用Hilbert能量谱和能量密度级的瞬态信号检测同样也可以大幅度提高瞬态信号的检测性能, 但是该方法相对于经验模态分解检测算法, 其复杂度和执行时间较高。

1 瞬态被动鱼声信号

图1和图2为食蚊鱼()和食人鱼()的求偶时发出的连续性重复被动鱼声信号以及岩豆娘鱼()和似鲤异吻象鼻鱼()摄食时发出的瞬态被动鱼声信号(鱼声数据来自于https: // www.soundeffects.ch), 图中幅值进行了归一化, 其采样频率为44.1 kHz, 图中可以看出连续性重复信号持续时间分布从100到400 ms, 而瞬态信号则表现为几毫秒时间的1~2个尖刺脉冲信号, 即周期性地发出声信号, 间隔时间长且短促, 非平稳性非常强。

2 Hilbert-Huang 变换分析方法

2.1 经验模态分解

针对信号局部均值和时间特征尺度与瞬时频率关系的研究, Huang引入了经验模态分解法(Empirical Mode Decomposition, EMD), 该法将一个瞬态信号分解成一系列固有模态信号(Intrinsic Mode Function, IMF)。

EMD分解的主要步骤为:

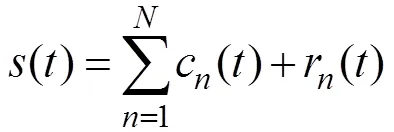
EMD的分解和重构实质上是筛分过程, 该方法其从特征时间尺度开始, 将瞬态信号中分离特征时间尺度逐渐增加的模态逐渐分离。

2.2 EMD 信号重构瞬态信号检测原理

相对于所采集的含噪的瞬态被动鱼声信号, 背景噪声呈现高频特性, 而EMD分解是根据时间尺度, 将局部时间尺度小的高频分量分解在低阶IMF中, 将局部时间尺度大的低频信号分量分解在高阶IMF中。根据EMD的这一特性, 对采样信号进行EMD分解, 然后对经验值的高阶IMF求和重构得到, 计算即可实现信号能量的检测。

2.3 基于能量密度级的瞬态信号检测

瞬时能量密度级是时间的函数, 是用来考察能量波动程度的量度。当有信号到达时, 样本会有很明显的能量波动, 因此将 Hilbert 谱的能量特性应用于瞬态信号检测, 其具体过程为对采样信号进行EMD分解, 对经验值的高阶IMF求和重构得到, 然后计算Hilbert 能量谱, 求瞬时能量密度级做能量密度级检测。

3 实验仿真

3.1 瞬时鱼声信号的EMD分解的时频域图

下面给出–10 dB信噪比条件下基于HHT的瞬态信号检测实例。瞬态信号模型的EMD分解结果, 如图3 所示, 共分解出9阶IMF和一个表示趋势的残余项, 图中给出前9阶。

通过仿真实验发现, 重构的阶数与信号长度有关, 本文中一般在第3~4阶时, IMF开始出现信号, 以下采用第4阶至最后一阶的IMF实现信号重构, 即得重构信号。

重构信号如图4所示, 将其与图中加噪声后的信号比较, 图中的原始信号几乎完全淹没在噪声背景中, 而图中的重构信号中, 被动瞬态鱼声信号比较清晰。经试验研究发现基于EMD分解的重构信号可以提高信号的信噪比, 且能提高瞬态信号的检测性能。

将前9阶IMF分别作傅里叶变换, 研究其频谱分布。图5中, IMF1 类似高通滤波器, 且频带较宽, 大部分噪声能量被滤到这一阶内。IMF2 到 IMF9 都是带通滤波器, 通带相互有重叠。因此该变换类似于多种滤波器的叠加滤波。

3.2 EMD检测被动鱼声瞬态信号

图6给出了不同信噪比瞬态信号和重构信号能量包络比较图。图中信噪比–20 dB时并未能检测到瞬时鱼声信号; –10 dB时噪声能量变化范围由原来的0.002下降到0.001左右, 减小了约50%, 含噪瞬态信号特征不明显, EMD重构后能检测到瞬时鱼声信号; 0dB时噪声能量变化范围由原来的0.001下降到几乎为0, 信号的能量同样有所下降, 由原来的0.003降至0.001, 减小了66%, 但是与噪声相比能量下降相对较小, 因此明显提高了瞬态信号的幅值。

仿真实验表明, 基于信号重构思想的瞬态信号检测, 提高了信号的信噪比, 检测概率和准确度都有明显改善, 基于Hilbert 黄变换的瞬态信号检测性能优于传统能量检测算法。

3.3 基于能量密度级的瞬态信号检测

仿真条件同上, 不同信噪比瞬态信号和重构信号比较图如图7所示。由图可见, 在 680~700点附近有较大的能量存在。沿着频率方向求积分, 得到能量密度级的时域图。

图7–10 dB瞬态信号组图中, 瞬时能量波动范围为0.023, 噪声为0.015, 信号与噪声相对值为1.53,图7(b)–10 dB重构信号组图中, 信号能量波动范围为0.011, 噪声能量为0.004, 信号与噪声相对值为2.75。因此, 基于Hilbert能量谱和能量密度级的瞬态信号检测也可以大大提高瞬态信号的检测性能, 但是该方法相对于EMD检测法来说算法的复杂度和执行时间有所提高。

4 结论

本文基于HHT的基本原理, 针对摄食、产卵和争斗过程中, 所发出的短促、瞬态的鱼声信号, 提出了基于HHT信号高阶重构和希尔伯特能量谱的被动瞬态鱼声信号检测方法。该方法利用 HHT 的不同阶数的滤波特性, 通过EMD分解出的IMF完成信号重构并由能量检测器实现鱼声瞬态信号检测, 此外通过将重构信号实现希尔伯特能量谱也可以实现瞬时能量密度级鱼声瞬态信号的检测。实验结果表明, 重构信号相比于原始信号相对于传统的能量检测器性能有所提高, EMD经验模态分解存在端点效应带来的误差, 有待进一步研究分析。

[1] Wood M L, Casaretto G, Horgan A D. Discriminating between fish sounds a wavelet approach[J]. Bioacoustics, 2002, 12: 337-339.

[2] Stolkin R, Radhakrishnan S, Sutin A, et al. Passive acoustic detection of modulated underwater sounds from biological and anthropogenic sources[C]//IEEE. Proceeding of Oceans. Vancouver: IEEE, 2007: 1-8.

[3] 任新敏, 高大治, 姚玉玲. 大黄鱼的发声及信号特性研究[J]. 大连水产学院学报, 2007, 22(2): 123-128. Ren Xinmin, Gao Dazhi, Yao Yuling. Occurrence and characteristic of sound in large yellow croaker[J]. Journal of Dalian Fisheries University, 2007, 22(2): 123-128.

[4] 王巍巍. 鱼类声信号的分析及特征提取研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. Wang Weiwei. Research of analysis and characteristics extraction on fish sound[D]. Harbin: Harbin Engineering University, 2008.

[5] 刘贞文, 许肖梅, 覃柳怀. 大黄鱼发声信号特性研

究[J]. 声学技术, 2010, 29(6): 342-343.Liu Zhenwen, Xu Xiaomei, Qin Liuhuai. Sound characteristics of the large yellow croaker[J]. Technical Acoustics, 2010, 29(6): 342-343.

[6] Rountree R A, Gilmore R G, Goudey C A, et al. Listening to Fish: Applications of passive acoustics to fisheries science[J]. Fisheries, 2006, 31(9): 433-446.

[7] 陈功, 常睿, 于海平, 等. 稀疏分解特征在鱼声端点检测中的应用[J]. 热带海洋学报, 2015, 34(4): 48-53. Chen Gong, Chang Rui, Yu Haiping, et al. Research on detection of weak passive fish acoustic by sparse decomposition feature[J]. Journal of Tropical Oceanography, 2015, 34(4): 48-53.

[8] 陈功, 常睿, 于海平, 等. 基于正弦函数基原子库微弱鱼声信号稀疏检测[J]. 中国测试, 2015, 41(6): 108- 112. Chen Gong, Chang Rui, Yu Haiping, et al. Sparse detection for weak passive fish acoustic signal based on sine wavelets[J]. China Measurement & Test, 2015, 41(6): 108-112.

[9] 陈功, 王平波, 庞韬, 等. 基于被动声学技术的海洋生物测量研究状况[J]. 渔业现代化, 2015, 41(6): 37- 42. Chen Gong, Wang Pingbo, Pang Tao, et al. Research progress of marine organisms based on passive acoustics technology[J]. Fishery Modernization, 2015, 41(6): 37-42.

[10] 薛飞. 基于希尔伯特黄变换的水声瞬态信号检测方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2009. Xue Fei. Research on the method of underwater acoustic transient signal detection based on Hilbert Huang Transform[D]. Harbin: Harbin Engineering University, 2009.

[11] Bouzid A, Ellouze N. Maximum error indiscrete EMD decomposition of periodic signals[C]//IEEE.15th International Conference on Digital Signal Processing.Cardiff: IEEE, 2007: 563-566.

[12] Kopsinis Y, Mclaughlin S. Enhanced empirical mode decomposition using a novel sifting-based interpolation points detection[C]. IEEE.14th Workshop on Statistical Signal Processing. Madison: IEEE. 2007: 725-729.

Research on the detection of weak transient passive fish acoustic signals based on Hilbert–Huang Transform

CHEN Gong1, 2, WANG Ping-bo2, BAO Yu-jun1, XU Qing-quan1, YANG Hui1, CHEN Zong-tao1

(1. Changzhou Institute of Technology, Changzhou 213022, China; 2. Xiamen University, Xiamen 361005, China; 3. Naval University of Engineering, Wuhan 430033, China)

To acquire transient passive fish acoustic signals during feeding and spawning, Hilbert–Huang Transform is introduced to detect weak signals. Firstly, Hilbert-Huang Transform analyzes the transient signals in the time-frequency domain by empirical mode decomposition. Energy detection is then realized by Hilbert–Huang Transform reconstruction from empirical high-level orders. In addition, Hilbert spectral analysis is proposed to detect transient signals and compared with a traditional energy method under a different signal-to-noise ratio (SNR). Finally, the feasibility and validity of the method are verified by processing experimental data.

passive transient fish acoustics; Hilbert–Huang Transform; signal-to-noise ratio (SNR); energy detector

(本文编辑: 刘珊珊)

Feb. 6, 2016

[National Natural Science Foundation of China, No.21305089; the Natural Science Foundation of Jiangsu Province, No.BK20130245; Key Laboratory of Underwater Acoustic Communication and Marine Information Technology (Xiamen University), Ministry of Education; Natural Science Foundation of Changzhou Institute of Technology, No.YN1513]

P756.6

1000-3096(2016)10-0091-06

10.11759/hykx20160106004

2016-01-06;

2016-07-09

国家自然科学基金(21305089); 江苏省自然科学基金青年基金(BK20130245); 水声通信与海洋信息技术教育部重点实验室(厦门大学); 常州工学院自然科学基金(YN1513)

陈功(1979-), 男, 江苏常州人, 博士, 副教授, 主要从事信号与信息处理的研究, E-mail: realchengong@sina.com