基于质子密度和弛豫时间的大脑MR图像分割新算法

周啸虎，高伟，张子齐

南京医科大学附属南京医院（南京市第一医院） 放射科，江苏 南京 210006

基于质子密度和弛豫时间的大脑MR图像分割新算法

周啸虎，高伟，张子齐

南京医科大学附属南京医院（南京市第一医院） 放射科，江苏 南京 210006

目的 本文提出一种基于聚类的无监督脑部MR图像分割新算法，有别于传统的基于灰度阈值和一维空间MR图像分割算法。方法 首先，估算输入图像的质子密度和弛豫时间； 然后，描述输入图像的概率分布；最后，采用基于空间关联决策准则识别最佳分类区域，达到图像分割的效果。结果 选用不同分割算法对人工合成图像和临床实例MR图像进行仿真实验。定性分析结果是本文算法的分割图像边缘和细节部分保存的完整清晰；定量评估结果显示基于 本文分割算法能获得探测率最大和误报率最小，且在15～30 dB信噪比范围内的戴斯相似性系数和杰卡德相似性系数均最大。结论 基于质子密度和弛豫时间的统计算法是一种可行的脑部MR分割算法，在噪声环境、图像灰度不均和临床实例等情况下均表现出强健性，具有较高的临床应用价值。

质子密度；弛豫时间；概率分布；空间关联准则；MR图像分割

0 引言

图像分割已广泛应用于图像引导介入、手术计划、放射治疗等方面[1-3]，其中脑部MR图像分割是评估脑白质病变的疗效和研究阿兹海默、精神分裂症等疾病随时间演变的一个基本定量工具，具体地说图像分割可以提供灰质、白质和脑脊液的容量分析，且能描述不同目标的形态学差异。

由于人工分割脑部MR图像伴随着主观差异大、耗时多等缺点，全自动分割技术能克服人工分割的不足，主要分为基于阈值、基于分类、基于区域、基于边缘等算法[4]。基于阈值的分割算法易于操作，但是很难确定一个合理的阈值。基于分类的基本分割算法有K均值聚类和高斯混合模型，但如果后处理方法选取不当，将会导致很差的分割效果。而且MR图像存在灰度不均、信噪比低等特点，同样增加了图像分割的难度。

本文提出一种基于分类的脑部MR分割新算法，主要利用质子密度（ρ）和弛豫时间（纵向弛豫时间T1和横向弛豫时间T2），而不是采集的灰度水平图像。利用弛豫时间改善分割性能的主要限制因素在于只是基于一维空间和后处理步骤的选取，本文提出的分割算法是基于ρ、T1和T2的3D空间，而不是加权图像，且引入一个新的距离判据作为分类度量标准。从几何角度讲，图像像素点投影到3D空间而不是一维线性能有效地增大每个类别之间的距离，提高分割和分类的精度[5]。在本文提出的分割算法中，分割区域的阈值是3D曲线，由ρ、T1、T2的联合统计分布函数自动确定，然后用于图像分割。

1 对象与方法

1.1 对象

为了定性、定量评估本文提出算法的可行性、强健性、降噪性和实用性，选用3组图像均在MATLAB平台上进行仿真实验。

（1）人工合成的大脑切片幻影图像，由4层组织构成，分别用蓝色、橙色、绿色和红色进行编码，且加入了均值为 30 dB的高斯噪声。

（2）选自BrainWeb数据库的4幅自旋图像，加入了均值为30 dB的高斯噪声和20%的灰度不均区域。

（3）来自30岁健康志愿者的四幅大脑自旋图像。3组图像尺寸均为512×512像素，具有512个灰阶。

1.2 方法

1.2.1 物理参数的计算

本文主要考虑采用自旋成像序列的MRI采集系统，成像过程中复杂信号的振幅可由2D傅里叶变换求得，信号振幅与组织参数ρ、T1和T2相关，此时单个像素（某层的单个体素）的振幅强度由公式（1）给出[6]。其中，TE和TR分别是MRI扫描中参数回波时间和脉冲重复间隔时间，θ = [ ρ T1T2]T是包含组织参数的一个向量。

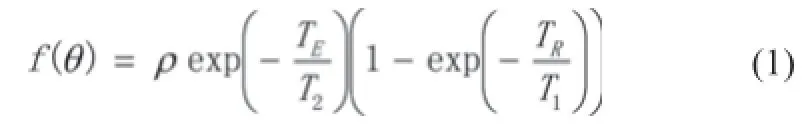
考虑到成像过程中伴随着噪声，MRI采集模型在复数域可由公式（2）给出。其中nR和nI代表噪声的实部和虚部，是独立分布的高斯变量，代表复数的角度。

θ采用最小二乘法估算，如公式（3）所示，M表示不同TE/TR组合所得的图像数目。

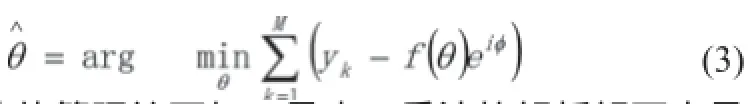
根据统计估算理论可知，最小二乘法的解析解可由最大似然估计和高斯分布求得[7-8]。当M足够大时，估算量具有无偏性和有效性，据此可推断出估计量、和满足已知均值和方差 的高斯分布，且均值μρ、μT1和μT2等于估计量参数值，方差和符合Cramer-Rao下界，主要取决于采集方式和噪声类型。由此可得随机变量、和的统计分布函数，公式（4）给出了的概率分布函数，和的概率分布函数同理可得。本文提出的分割算法在于利用公式（4）在3D空间上发现最佳的决策区域[9-10]。

1.2.2 距离决策准则

基于3个估计量之间在统计学上两两独立的假设，引入蒙特卡洛模拟方法[11]。在每一个周期内，质子密度和自旋弛豫时间均被估算，计算结果见图1。观察（p，T2）散点图，容易看出存在一个非最小相关性，和的相关系数为-0.844，由此相关性可知存在统计相关性。在此种情况下，多元高斯统计分布的协方差矩阵Σ是完全填充的，因此推导出基于统计相关性的决策准则，如公式（5）所示，式中Cov（i，j）表示估计量i和j的协方差。

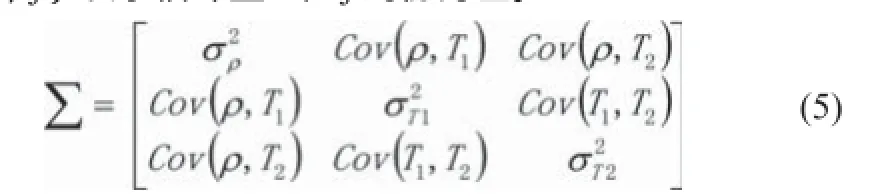
图1 ( ρ，T2) 的估算值

分割结果由公式（6）的最小值计算所得，运用公式（6）后决策区域的变化，见图2。4个参考组织由不同的（ρ，T2）组合构成，根据空间中每个点到4个参考组织中心点（图中星号）的距离进行图像聚类分割。

为了提高分割性能，在基于统计相关性的基础上，提出基于空间相关性的概率正则化准则。主要包含4个步骤：① 定义单个像素的领域空间，本文采用8邻域；② 定义每个像素点到中心像素点的最小距离为d0，p(n)是第n层像素在8邻域空间内的比重，p(n)∈[0,1]；③ 如果邻域内绝大多数像素属于同一个类别，将缩短此类别的距离来调整结果，减少量不能超过事先设定的阈值d0；④ 运用公式（7）求得分割结果。

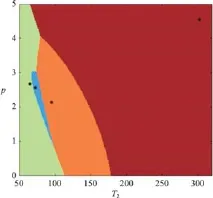
图2 基于统计相关性的决策区域

2 结果与分析

基于分类思想的分割算法是无监督的，分类决策准则起关键作用。将本文提出的基于空间相关性准则（Spatial Correlation Based Criterion，SpCC）与基于最小欧氏距离（Minimum Euclidean Distance Approach，MED）、基于加权距离(Weighted Distance Based Criterion，WDC)、基于统计相关性（Statistical Correlation Based Criterion，StCC）等进行比较，并与经典的K均值聚类算法（K-means）进行比较。脑MR图像分割性能由探测率、误报率、戴斯相似性系数和杰卡德相似性系数进行定量评估。

2.1 第一组合成图像分割效果比较

为了验证本文分割算法的优越性，首先人工合成一幅大脑皮层幻影作为参考图像，图中包含的4种组织分别用蓝色、橙色、绿色和红色进行编码。应用公式（3）最小二乘法即可求得参考图像对应的ρ、T1和T2参数图，见图3；基于不同算法的图像分类分割结果，见图4；不同算法对4种组织分割性能的定量评估，见图5；对不同信噪比情况下算法稳定性进行了测试，见图6。

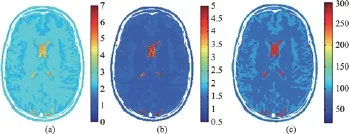
图3 估算的质子密度图（a）、T1图（b）、T2图（c）

图4 不同算法的分类分割结果

图5 大脑幻影中不同组织的分类性能比较

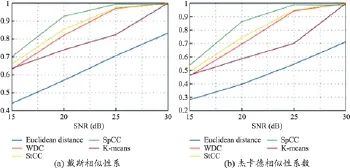
图6 不同信噪比对应的相似性系数变化

从定性角度看图4（e）边缘轮廓清晰，小细节部分保存完整，所有的区域均被准确分割，分割效果最优；图4（b）～（d）和（f）中均出现蓝色和橙色误分类现象，且K均值聚类算法对红色和绿色组织具有良好的分割效果，这是由于分类决策准则无法精确分离相邻区域（图2）；图5从定量角度再次证明本文算法优良的分割性能，不同组织的探测率、误报率、戴斯相似性系数和杰卡德相似性系数均最佳。观察图6可知，不同算法的戴斯相似性系数和杰卡德相似性系数均和信噪比成正相关，在15～20 dB区间内，基于本文算法的增长率最大，到达25 dB时趋于稳定，K均值算法虽然在30 dB时达到最大，但是对噪声非常敏感，由此可验证本文算法具有很强的强健性。统计分布越多，图像分类分割的效果越佳。

2.2 第二组人工合成图像分割效果比较

第二组人工合成图像选自BrainWeb网站，图像中包含20%灰度不均的区域，主要位于图像左下角，仿真实验结果,见图7。其中K均值算法所受影响最大，灰度不均匀区域中的绿色部分几乎全部丢失，然而本文的分类分割算法仍然优越。

图7 对BrainWeb幻影图像的分类分割结果

2.3 临床实例结果

实例图像来自一位30岁健康男性的大脑自旋MR图像，图像分割为脑白质、脑灰质和脑脊液3个区域，此处仅用本文提出的分类算法与K均值算法进行比较，实验结果见图8。其中K均值算法获得低正则化的分割区域，对脑灰质和脑脊液区域分割精确度很差；然而基于本文算法的脑灰质和脑脊液分割性能明显提高。两种算法都存在将脑白质误划分为脑灰质的现象，若使用更精确的正则化规则，则可以获得更佳的分割性能，提示本文基于多维距离决策准则是有前景的。

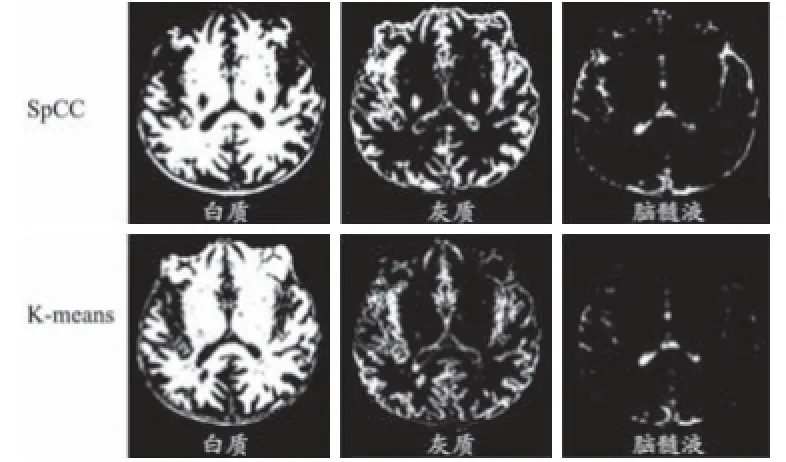
图8 临床实例图像分割结果

3 结论

本文提出了一种无监督分类算法，用于脑部MR图像分割，主要特点在于将探测准则应用于估算质子密度图和弛豫时间图，而不是采集到的灰度水平图像；并且尝试采用基于质子密度和弛豫时间的三维距离作为分类判别准则，而不是一维距离。人工合成图像和临床实例仿真实验结果表明基于本文提出的分类分割算法分割精度高、稳定性强，能获得优质的分割图像，满足临床诊断需求。

[1] Baselice F,Ferraioli G,Pascazio V.A Novel Statistical Approach for Brain MR Images Segmentation Based on Relaxation Times[J]. Biomed Res Int 2015,2015(1):154614.

[2] Akhondi-Asl A,Warf eld SK.Estimation of the Prior Distribution of Ground Truth in the STAPLE Algorithm: An Empirical Bayesian Approach[A].Medical image computing and computer-assisted intervention:MICCAI[C]. Berlin:Springer,2012:593-600.

[3] 刘建磊,隋青美,朱文兴,等.结合概率密度函数和主动轮廓模型的磁共振图像分割[J].光学精密工程,2014,22(12):3435-3443.

[4] Serag A,Blesa M,Moore EJ,et al.Accurate Learning with Few Atlases (ALFA): an algorithm for MRI neonatal brain extraction and comparison with 11 publicly available methods[J].Sci Rep,2016,6:23470.

[5] 张建伟,杨红,陈允杰,等.结合非局部信息的脑MR图像分割与偏移场恢复耦合模型[J].计算机辅助设计与图形学学报, 2013,25(4):526-532,540.

[6] 贺振华,黄英,刘林,等.一种改进的分水岭算法在医学图像分割中的应用研究[J].工业控制计算机,2013,26(5):99-100,103.

[7] 李杰,陈国栋.基于改进区域生长算法的肝脏管道图像分割方法[J].中国医疗设备,2014,29(10):19-23.

[8] 彭莹莹,张书旭,余辉,等.PET/CT图像分割技术在肺癌放疗计划中的应用[J].中国医疗设备,2014,29(6):160-163.

[9] 李强.医学图像分割进展[J].中国医疗设备,2010,25(5):121-124,120.

[10] 伍强,陈赛明,涂蓉,等.FCM和Level Set在医学影像分割中的应用[J].中国医疗设备,2012,27(9):38-41.

[11] Tian Z,Liu L,Fei B.A supervoxel-based segmentation method for prostate MR images[J].SPIE Med Imaging,2015,9413:941318.

A Novel Approach for Brain MR Image Segmentation Based on Proton Density and Relaxation Time

ZHOU Xiao-hu, GAO Wei, ZHANG Zi-qi
Department of Radiology, Nanjing First Hospital, Nanjing Medical University, Nanjing Jiangsu 210006, China

Objective This paper proposed a brain joint segmentation and classif cation algorithm based on proton density (ρ) and relaxation time (T1) and (T2), instead of the acquired gray level image. Methods Estimation of proton density and relaxation time was made, then the approach exploited the statistical distribution of the involved signals in the complex domain; at last a novel method for identifying the optimal decision regions was proposed, which could achieve the ideal segmentation results. Results Both simulated and real datasets were evaluated by using different methods. Qualitative analysis showed that edges were well retrieved and small structures were preserved and completely clear. Quantitative evaluation results showed that the proposed segmentation algorithm in this paper could provide the best detection probability and false alarm probability. And it could acquire the maximal Dice coeff cient and Jaccard similarity indexes in case of different SNR (15～30 dB). Conclusion The proposed method based on ρ, T1and T2maps was a feasible segmentation algorithm. And it could provide better robustness in the noise environment, intensity inhomogeneity and clinical applications, which was of great value in clinical popularization.

proton density; relaxation time; statistical distribution; spatial correlation; MR image segmentation

R318；TP391

A

10.3969/j.issn.1674-1633.2016.10.008

1674-1633(2016)10-0025-04

2016-06-07

2016-06-19

张子齐，副主任技师，主要研究方向为医学影像图像采集与PACS网络及图像存储。

通讯作者邮箱：zhangziqi2001@aliyun.com