可变几何通道控制执行装置动态特性研究
2017-01-18张伟周振华邹品文韩小曼吕宇
张伟,周振华,邹品文,韩小曼,吕宇
(贵州红林机械有限公司,贵阳550009)
可变几何通道控制执行装置动态特性研究
张伟,周振华,邹品文,韩小曼,吕宇
(贵州红林机械有限公司,贵阳550009)
可变几何通道控制执行装置的动态特性,直接影响到航空发动机的进气和排气性能。以一几何通道控制执行装置为研究对象,阐述了其基本结构和工作原理;建立了可变几何通道控制系统数学模型,并运用AMESim建立其仿真模型,重点分析了油嘴Ⅰ直径、油嘴Ⅱ直径、作动筒活塞杆直径、作动筒活塞直径、负载等参数,对可变几何通道控制执行装置动态特性的影响,为同类产品的设计、改进、改型和性能优化提供了理论依据。
航空发动机;控制系统;几何通道控制执行装置;动态特性;作动筒;活塞杆全程移动时间
1 引言
航空发动机可变几何通道控制系统是发动机控制系统中非常重要的组成部分,可实现对进口导向叶片、喷口喉道面积的控制和调节,对叶尖间隙的主动补偿和调节等。
某型发动机几何通道用3个作动筒控制,对几何通道的控制要求为两级控制,对应作动筒活塞杆的位置为完全伸出或完全回缩两个状态。最大负载下,作动筒活塞杆从完全回缩位置到完全伸出位置或由完全伸出位置到完全回缩位置的动作时间要求为1.5±0.2 s,对应几何通道从最小状态到最大状态或由最大状态到最小状态的时间要求为1.5±0.2 s。要求几何通道控制装置掉电时,作动筒处于伸出状态。根据被控制对象使用需要,本文开展并完成了可变几何通道控制执行装置的设计,并针对关键结构参数对其动态特性的影响进行了深入研究。
2 可变几何通道控制执行装置工作原理
可变几何通道控制执行装置原理见图1,主要由转换活门、弹簧、油嘴I、油嘴Ⅱ、油嘴Ⅲ、转换活门衬套、电磁阀组成。
电磁阀不工作(不通电)时,电磁阀的A口与B口沟通,转换活门左腔通过电磁阀与低压燃油系统沟通,转换活门在弹簧力的作用下工作于左极限位置。此时,高压燃油经高压油进口,沿图1中红色箭头标示方向通过转换活门衬套左端控制窗口、油嘴Ⅱ流进作动筒无杆腔,作动筒有杆腔沿图1中蓝色箭头标示方向经过油嘴I、转换活门右端控制窗口流道与低压燃油系统沟通,作动筒活塞杆在液压力的作用下处于伸出位置。该状态满足几何通道控制逻辑“几何通道控制装置掉电时,作动筒处于伸出状态”的要求。
电磁阀工作(通电)时,电磁阀的A口与B口被截断,转换活门左腔与低压燃油系统不沟通,高压燃油经高压油进口、油嘴Ⅲ进入转换活门左腔,转换活门在左腔液压力的作用下移动到右极限位置(图2)。此时,高压燃油经高压油进口沿图2中红色箭头标示方向通过转换活门衬套右端控制窗口、油嘴I进入作动筒有杆腔,作动筒无杆腔沿图2中蓝色箭头标示方向经过油嘴Ⅱ、转换活门衬套左端控制窗口流道与低压燃油系统沟通,作动筒活塞杆在液压力的作用下处于回缩位置。
通过控制电磁阀通电和断电,改变进入作动筒有杆腔和无杆腔控制油的流动方向,控制作动筒活塞杆的伸缩状态,实现对发动机几何通道的控制。
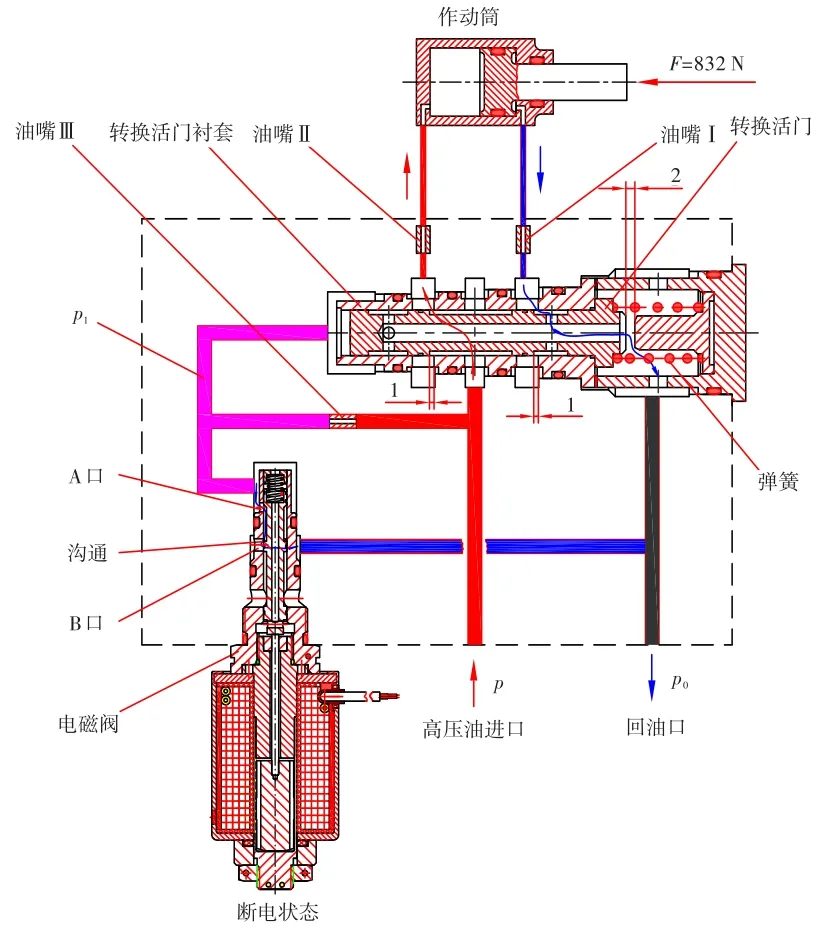
图1 可变几何通道控制执行装置原理图Fig.1 Schematic diagram of the variable geometry channel control executive device
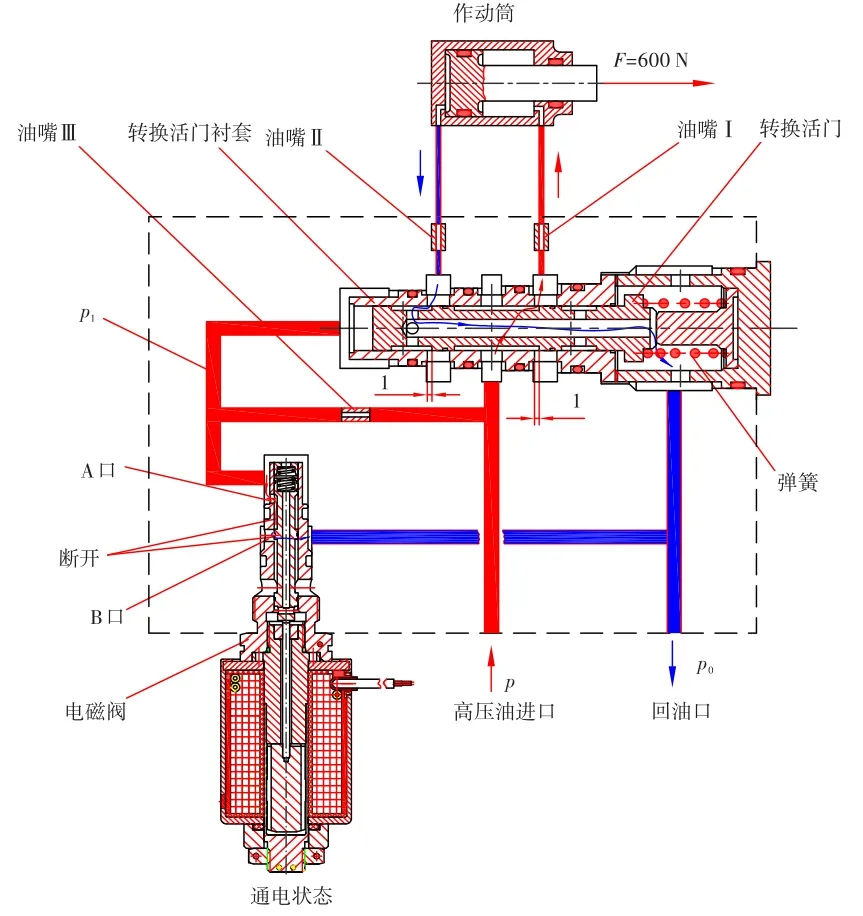
图2 转换活门在右极限位置原理图Fig.2 Schematic diagram of switch valve at the right limit position
3 可变几何通道控制系统数学模型的建立
在对可变几何控制执行装置的组成、功能和原理进行详细分析的基础上,以流量连续方程和力平衡方程为基础[1],建立该系统的数学模型。
3.1 主要零组件参数的确定
该装置工作介质为3号喷气燃料,工作介质(燃油)重度ρ=7 693 N/m3,高压油进口燃油压力p= 5.5 MPa,低压燃油系统(回油系统)燃油压力p0= 0.3 MPa。
作动筒活塞直径15.0 mm,活塞杆直径8.0 mm,活塞杆最大行程17.5 mm,活塞杆伸出时最大负载F伸=832.0 N,活塞杆回缩时最大负载F缩=600.0 N。
选用某成熟电磁阀的性能参数为:额定工作压力6.0 MPa,额定流量5 L/min,吸合和释放时间3~5 ms,工作电压27±3 VDC。
设计的转换活门(图3)直径10.0 mm,控制凸肩宽4.8 mm。转换活门衬套(图4)左、右端控制窗口数各2个,窗口纵向尺寸4.8 mm,窗口周向尺寸3.0 mm。
3.2 弹簧参数的确定
图1所示为该几何通道控制装置的初始状态,此时电磁阀断电,转换活门在弹簧力作用下处于最左端位置。设p1=2.0 MPa。为保证转换活门工作在最左端位置,弹簧预压力需大于Fmin。根据公式(1),Fmin=133.5 N。因此,初设弹簧预压力F=200.0 N,弹簧刚度K=50 N/mm。
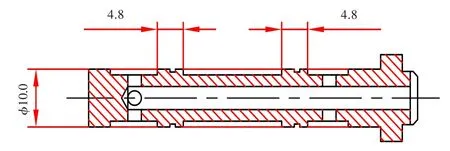
图3 转换活门尺寸Fig.3 Dimensions of the switch valve
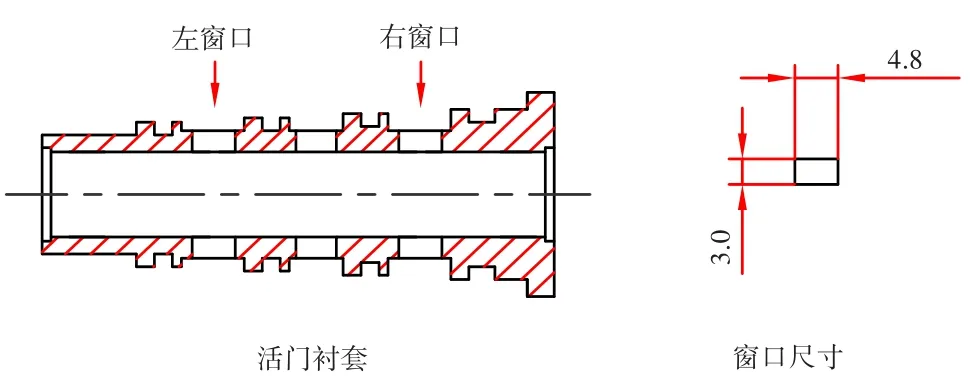
图4 转换活门衬套尺寸Fig.4 Dimensions of the switch valve bushing

式中:A为转换活门截面积,且A=78.5 mm2。
3.3 断电状态电磁阀的等效流通面积
电磁阀不通电(不工作)时A口与B口连通。设A口与B口连通时其等效流通面积为A3,根据流量公式可计算出A3:

式中:Q为6.0 MPa额定工作压力下的电磁阀流量,Q=5.0 L/min;μ为流量系数,与型孔形状、位移、型孔前后压差、液体粘度等因素有关[2-3],本文取0.7;g为重力加速度,取9.8 m/s2;Δp为电磁阀进出口(A口和B口)之间的压差,此处Δp=6.0 MPa。由此可得A3= 1.123 mm2。
3.4 油嘴Ⅲ的等效流通面积
在忽略转换活门和电磁阀泄漏的情况下,由高压油进口通过油嘴Ⅲ的燃油全部通过电磁阀流到低压燃油系统,即其相互关系可简化为图5所示。
根据通过油嘴Ⅲ和电磁阀的流量相等(式(3)),可得A4=0.780 mm2。
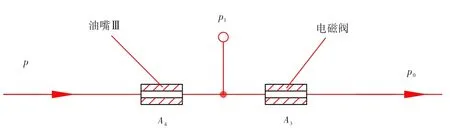
图5 油路关系图Fig.5 Relationship diagram of the oil line
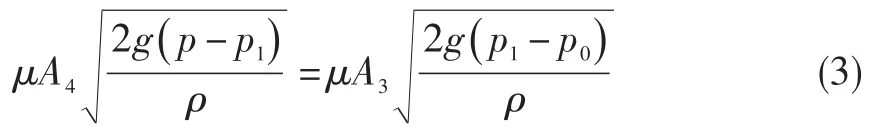
3.5 作动筒活塞杆回缩移动时间
在图2所示工作状态,电磁阀通电,电磁阀A口和B口之间断开,此时高压油经过油嘴Ⅲ进入转换活门左腔,推动转换活门向右移动。转换活门的移动量为2.0 mm,在移动前1.0 mm的过程中进入作动筒有杆腔和无杆腔的燃油流向不变,作动筒活塞不会移动。从转换活门移动到1.0 mm之后,进入作动筒有杆腔和无杆腔的燃油流向改变,作动筒活塞杆开始移动。如果从电磁阀收到电信号开始计算,理论上作动筒活塞杆从完全伸出状态到完全缩回状态的移动时间t回,等于转换活门从左极限工作位置移动到右极限工作位置所需时间t1,加上转换活门移动到右极限位置后燃油完全充满有杆腔时间t2。
3.5.1 转换活门移动时间
转换活门从左极限工作位置到右极限工作位置的移动距离为2.0 mm,在忽略泄漏的情况下,活门从左极限工作位置移动到右极限工作位置过程中,流入转换活门左腔的燃油体积VQ=0.157 cm3。电磁阀A、B口关闭后,p1压力迅速上升到p2(转换活门开始移动时左腔燃油压力)。由于燃油几乎不可压缩,p1上升到p2的时间也可忽略。当活门右端与限位块刚接触时,活门移动量为2.0 mm,此时p2压力上升到p3(转换活门右端移动至与限位块左端距离刚为0时)。通过式(4)、式(5)可得,p2=2.85 MPa,p3=4.12 MPa。
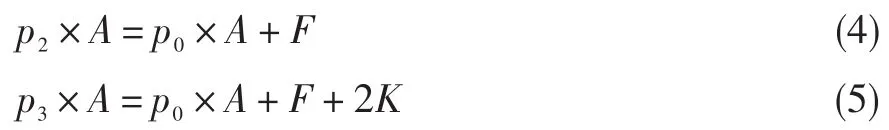
假设p2上升到p3的规律如图6所示,则转换活门左腔燃油压力变化方程为:

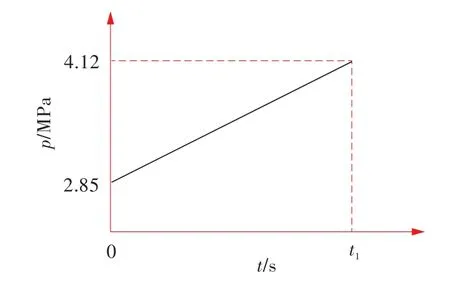
图6 p2上升到p3的曲线Fig.6 Curve fromp2top3
式中:t1为转换活门左腔燃油压力从2.85 MPa变化到4.12 MPa所需时间,也即转换活门从左极限工作位置移动到右极限工作位置所需时间。
根据t1时间内流经油嘴Ⅲ的燃油量等于VQ(式(7))计算,得到t1=4.7 ms。

式中:Δp=p-p左=2.65-1.27t/t1,A2为活塞杆面积且A2=50.26 mm2。
3.5.2 转换活门从左极限工作位置到刚移动1.0 mm的时间
根据3.5.1节计算结果,p左=270.2t+2.85。据此可得转换活门右移过程中经过油嘴Ⅲ的流量方程:
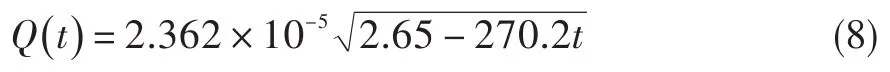
设t3时间内流过油嘴Ⅲ的燃油体积为Vt3,则有:
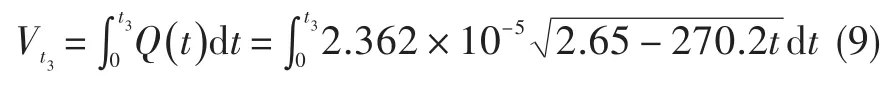
由Vt3=VQ/2,可得t3=2.165 ms。
3.5.3 燃油完全充满有杆腔的时间
由图2可知,转换活门从左极限位置移动到右极限位置的距离为2.0 mm,其中转换活门在移动第1个1.0 mm过程中进入作动筒有杆腔和无杆腔的燃油流向保持不变。从移动第2个1.0 mm开始,进入作动筒有杆腔和无杆腔的燃油流向反向,高压油经转换活门右控制窗口进入作动筒有杆腔,作动筒无杆腔经转换活门左控制窗口与低压燃油系统沟通。因此可以得到方程:

式中:p有、p无分别为作动筒有杆腔和无杆腔内的燃油压力,A1为活塞面积且A1=176.7 mm2。
因为作动筒有杆腔和无杆腔移动距离相等,由此可得:
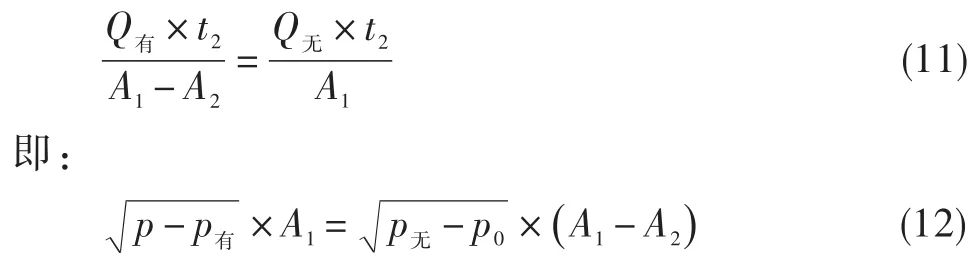
联立式(10)、式(12)可得,p有=5.409 MPa,p无= 0.475 MPa。
根据前文计算,转换活门从左向右移动第2个1.0 mm所花时间(t1-t3)=2.535 ms。为简化计算,假设转换活门从左向右移动第2个1.0 mm为匀速运动,则其运动速度为0.394 5 m/s。
根据转换活门移动速度、控制窗口的数量和尺寸,可列出活门移动过程中控制窗口面积随时间变化的方程:

由式(14)可得,转换活门移动完第2个1.0 mm位移后,流入作动筒有杆腔的燃油体积V=0.013 4cm3。

作动筒有杆腔的总容积为6.638 cm3。转换活门移动完第2个1.0 mm位移后,已经有0.013 4 cm3的燃油流进作动筒有杆腔,因此转换活门移动结束,即控制窗口开到最大后(此时窗口面积为6.0 mm2),还需6.624 6 cm3的燃油流进作动筒有杆腔,作动筒活塞杆才能完成全部回缩。控制窗口达到最大后,若不计燃油从进口到作动筒有杆腔的压力损失,根据式(15),可得到此时流入作动筒有杆腔的流量Q= 64.158 cm3/s。由此得到t2=0.103 3 s,t回=0.108 0 s。

由此可以看出,在没有油嘴I和油嘴Ⅱ的情况下,作动筒活塞杆的回缩速度很快,全程回缩时间远小于1.5±0.2 s。
另外,在图2工作状态,当电磁阀断电,电磁阀A口和B口之间沟通,此时转换活门左腔与低压燃油系统之间连通,转换活门左腔燃油压力由5.5 MPa下降到2.0 MPa。此过程中,当转换活门左腔燃油压力下降到p3时,活门开始左移。从电磁阀断电到转换活门移动到左极限位置,通过电磁阀流到低压燃油系统的燃油量为通过油嘴Ⅲ的燃油量与转换活门移动排出的燃油量之和,根据该关系及前述类似方法,可计算出转换活门移动时间、转换活门移动第2个1.0 mm过程中进入作动筒无杆腔的燃油量,最终计算出作动筒活塞杆从完全回缩状态到完全伸出状态移动时间。
4 可变几何通道控制执行装置动态特性研究
4.1 模型验证
采取仿真方法验证上述数学模型的正确性。运用AMESim软件建立了仿真模型[4-5],见图7。模型采用AMESim液压元件构造库中的元件,按照元件实际结构进行搭建,并依据元件设计图中的几何尺寸确定模型结构参数。图8和图9为仿真过程中得到的作动筒有杆腔压力曲线、作动筒无杆腔压力曲线、转换活门左腔压力曲线、作动筒回缩移动时间曲线、转换活门移动时间等,可见仿真结果与数学模型计算结果基本一致。
通过仿真模型计算,得到油嘴I直径为1.25 mm、油嘴Ⅱ直径为0.7 mm时,作动筒活塞杆正反向动作时间满足1.5±0.2 s的要求。作动筒移动时间曲线见图10,与产品工程试验结果一致。
4.2 结构参数对可变几何通道控制执行装置动态特性的影响
4.2.1 油嘴I直径的影响
油嘴I与作动筒的有杆腔相连,得到油嘴I直径对作动筒移动时间的影响曲线,见图11。可见,随着油嘴I直径的增大,作动筒正反向移动时间有减小的趋势,但变化较微小。
4.2.2 油嘴Ⅱ直径的影响
油嘴Ⅱ与作动筒的无杆腔相连,得到油嘴Ⅱ直径对作动筒移动时间的影响曲线,见图12。可见,随着油嘴Ⅱ直径的增大,作动筒正反向移动时间均变短。
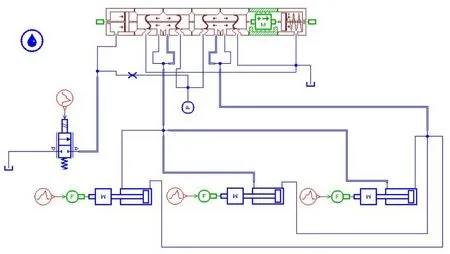
图7 可变几何通道控制执行装置仿真模型Fig.7 Simulation model of the variable geometry channel control executive device
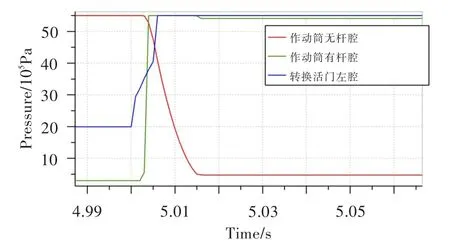
图8 仿真压力曲线Fig.8 Pressure curve

图9 仿真时间曲线Fig.9 Time curve
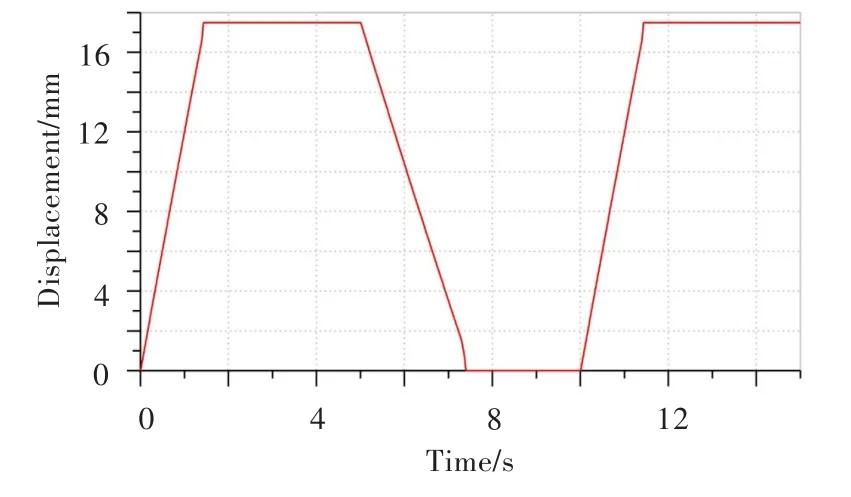
图10 作动筒正反向移动时间曲线Fig.10 Time curve of actuator forward and backward moving
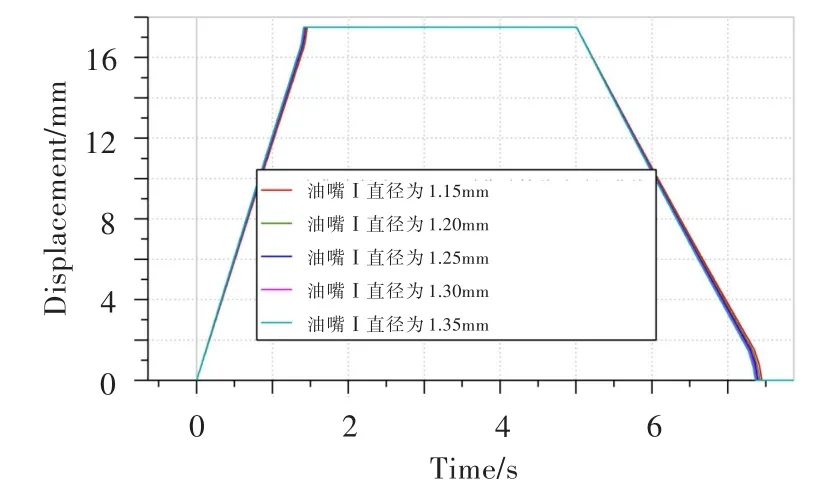
图11 油嘴Ⅰ直径对作动筒移动时间的影响Fig.11 The influence of nozzleⅠdiameter on actuator moving time
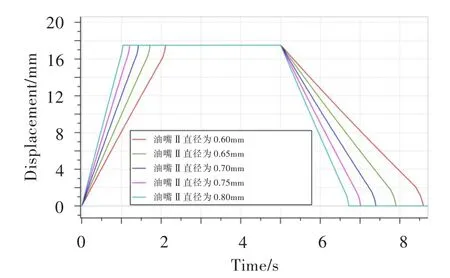
图12 油嘴Ⅱ直径对作动筒移动时间的影响Fig.12 the influence of nozzleⅡdiameter on actuator moving time
4.2.3 作动筒活塞杆直径的影响
作动筒活塞杆直径大小影响活塞受力,仿真得到作动筒活塞杆直径对作动筒移动时间的影响曲线,见图13。可见,随着作动筒活塞杆直径的增大,作动筒正向移动时间几乎不受影响,但反向移动时间不断增大。
4.2.4 作动筒活塞直径的影响
作动筒活塞直径大小影响活塞受力,仿真得到作动筒活塞直径对作动筒移动时间的影响曲线,见图14。可见,随着作动筒活塞直径的增大,作动筒正反向移动时间不断减小。
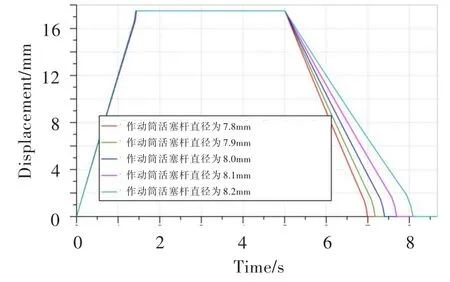
图13 作动筒活塞杆直径对作动筒移动时间的影响Fig.13 The influence of piston rod diameter on actuator moving time
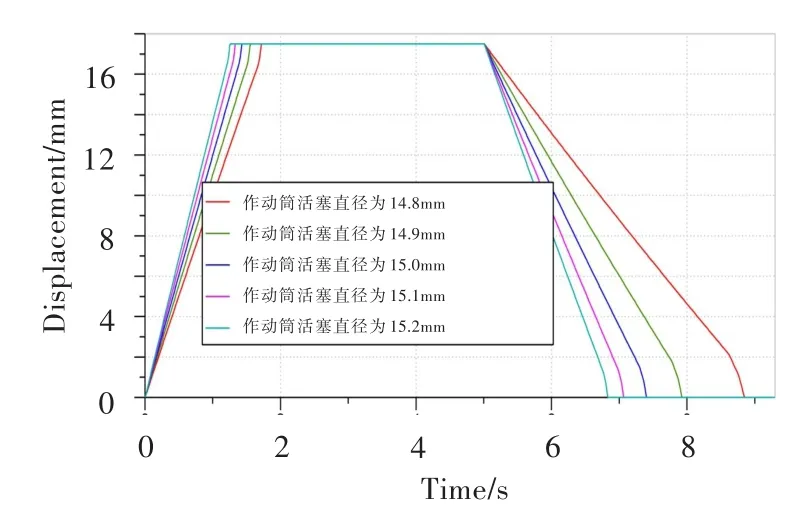
图14 作动筒活塞直径对作动筒移动时间的影响Fig.14 The influence of piston diameter on actuator moving time
4.2.5 负载的影响
仿真得到的负载对作动筒移动时间的影响曲线见图15。可见,随着作动筒伸出负载的增大,作动筒正向移动时间不断增大,反向移动时间不受影响;随着作动筒缩回负载的增大,作动筒正向移动时间不受影响,反向移动时间不断增大。
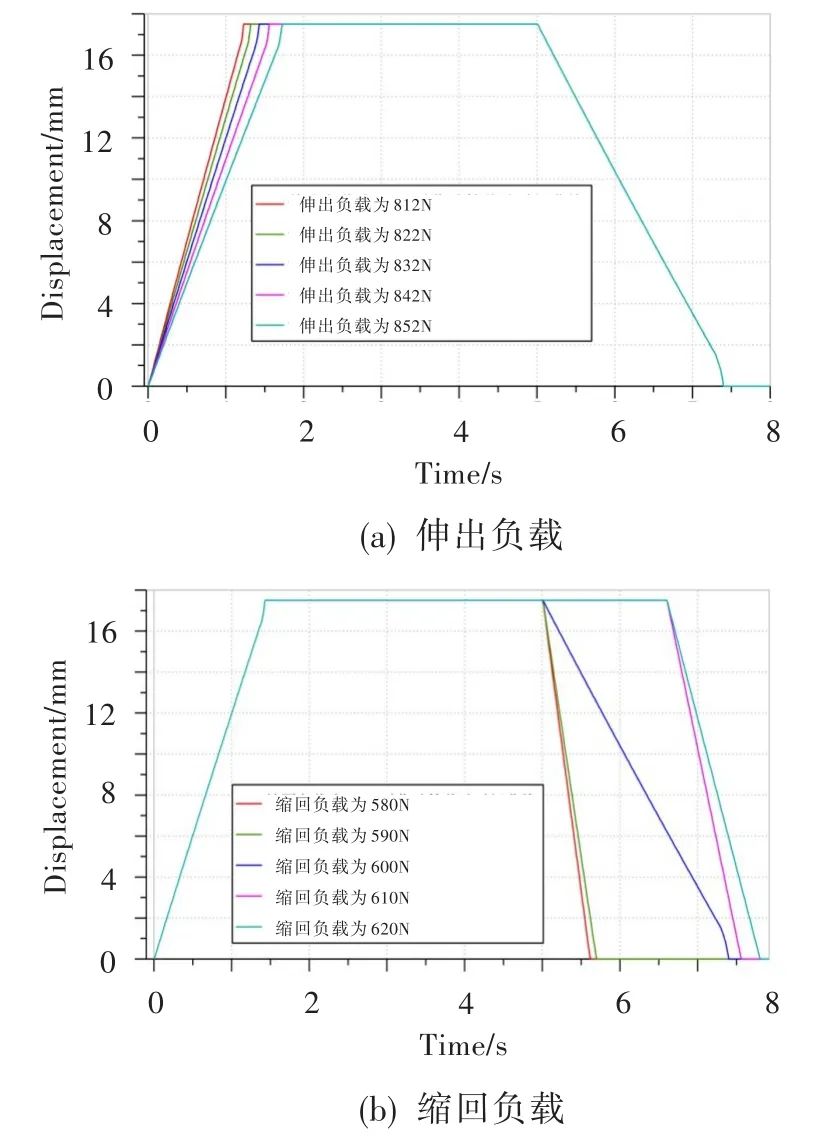
图15 作动筒负载对作动筒移动时间的影响Fig.15 The influence of retracted load on actuator moving time
5 结论
建立了可变几何通道控制系统的数学模型和仿真模型,针对油嘴I直径、油嘴Ⅱ直径、作动筒活塞杆直径、作动筒活塞杆直径、负载等参数,对可变几何通道控制系统动态特性的影响进行了研究,为工程实践中航空发动机可变几何通道控制执行装置的设计及故障分析提供了依据,可为同类产品的工程设计提供参考。主要研究结论为:
(1)作动筒正向移动时间随着油嘴I直径、油嘴II直径、活塞直径的增大而减小,其中油嘴I直径的影响较小;随着作动筒伸出负载的增大而增大。
(2)作动筒反向移动时间随着油嘴I直径、油嘴Ⅱ直径、活塞直径的增大而减小,其中油嘴I直径的影响较小;随着活塞杆直径、缩回负载的增大而增大。
(3)作动筒的移动时间主要通过油嘴Ⅱ直径大小来调节,可以通过油嘴I直径大小来微调;作动筒的移动时间与作动筒的活塞直径、活塞杆直径、负载均有关。
(4)正反方向移动时间之差无法通过油嘴I直径、油嘴Ⅱ直径来调节。确定设计参数时,应对正反向移动时间分别规定,规定正反方向移动时间之差要求时,应充分考虑作动筒参数和负载对正反方向移动时间之差的影响。
[1]马静,王镛根.某导弹燃油调节器的建模及仿真研究[J].计算机仿真,2003,20(9):35—38.
[2]葛树宏,樊丁,彭凯.某型航空发动机燃油调节器改型设计研究[J].计算机仿真.2012,8(29):81—84.
[3]樊思齐,李华聪,樊丁.航空发动机控制[M].西安:西北工业大学出版社,2008.
[4]付永领,祁晓野.AMESim系统建模和仿真——从入门到精通[M].北京:北京航空航天大学出版社,2006.
[5]陈宏亮.X-8航空发动机燃油调节系统建模仿真研究[D].西安:西北工业大学,2006.
Dynamic characteristics of variable geometry channel control executive device
ZHANG Wei,ZHOU Zhen-hua,ZOU Pin-wen,HAN Xiao-man,LV Yu
(Guizhou Honglin Mechinery Corporation Ltd.,Guiyang 550009,China)
The dynamic characteristics of variable geometry channel control executive device directly affect the intake and exhaust performance of aero-engine.Taking a geometry channel control executive device as the research object,the basic structure and working principle were elaborated;the mathematical modeling and simulation model were established by using the AMESim.The design parameter influences of nozzleⅠdiameter,nozzleⅡdiameter,actuator piston rod diameter,actuator piston diameter and load on variable geometry channel control executive device dynamic characteristics were analyzed to provide theoretical basis for same products design,improvement,retrofit and performance optimization.
aero-engine;control system;geometry channel control executive device;dynamic characteristic;actuator;full moving time of piston rod
V233.7
A
1672-2620(2016)06-0038-06
2015-10-29;
2016-12-15
张伟(1982-),贵州安顺人,工程师,主要从事航空发动机燃油控制系统液压机械附件设计研究。
