灰色神经网络在MBR曝气强度中的应用研究

史亚威+李春青

摘 要：曝气是MBR膜污染的操作条件影响因子中的一个重要参数，曝气强度过大易造成膜丝断裂，过小又不能减缓膜污染。针对该问题，本研究首先运用灰色模型对中空纤维膜不同使用阶段中的最佳曝气强度值进行粗略预测。再将影响膜过滤性能的三个因素作为BP神经网络的输入，不同膜清洗次数后的最佳曝气强度作为输出，进行曝气的BP网络模型预测。最后将灰色模型的预测值及影响膜过滤性能的三个因素作为灰色神经网络的输入，最佳曝气强度作为输出，进行曝气的灰色神经网络预测。通过对两个神经网络模型的预测结果对比分析，得出结论灰色神经网络模型优于BP神经网络模型。

关键词：MBR：膜污染：曝气强度：灰色系统：灰色神经网络

中图分类号：TP389.1 文献标识码：A

1 引言（Introduction）

MBR污水处理技术问世以来，膜污染问题一直是其发展的瓶颈，其导致膜通量下降，增加组件更换和清洗的频率，从而增加运行费用[1，2]。在MBR处理废水的实际生产过程中，膜组件的过滤性能会随着膜清洗次数的增加而逐渐衰减，随之也导致膜通量的下降。兼顾于膜通量与减缓膜污染的目的，在每次清洗之后的再使用过程中设置合适曝气的强度有利于延缓膜污染[3]。

针对曝气强度的预测研究，首先使用GM（1，1）灰色系统预测每个阶段最佳曝气强度的变化趋势。GM（1，1）作为灰色系统理论的重要内容，其突出特点是建模过程简单，模型表达简洁，便于求解，应用广泛[4]。BP神经网络在预测领域有着比较成熟的应用[5]，因此再建立输入为膜清洗的次数、膜清洗时长、膜清洗药剂浓度，输出为最佳曝气强度的BP预测模型。最后建立灰色系统与BP结合的灰色神经网络模型，并经过实验对比分析两个神经网络模型的预测识别正确率。

2 最佳曝气强度（Optimum aeration intensity）

浸没式MBR运行过程中，曝气量过大，易导致污泥破碎，影响混合液过滤特性，进而加剧膜污染，降低膜通量。曝气量过小又会导致溶解氧不足，必将对物生物的降解产生不利影响，增加膜的负荷，易造成膜污染，从而影响污水处理的效果[6]。因此确定最佳的曝气强度不仅利于减小膜污染还有利于保持较高的膜通量。

2.1 最佳曝气强度影响因素

为有效的控制膜污染，最佳曝气强度值会受到膜过滤性能的影响，而影响膜过滤性能的主要因素包括膜清洗的次数、每次膜清洗时长、膜清洗药剂浓度。其中由于膜的不可避免的污染趋势，其性能会随着膜清洗次数的增大而衰减，从而清洗过后的再使用阶段需要相应的增加曝气强度值。

2.2 最佳曝气强度值的实验确定

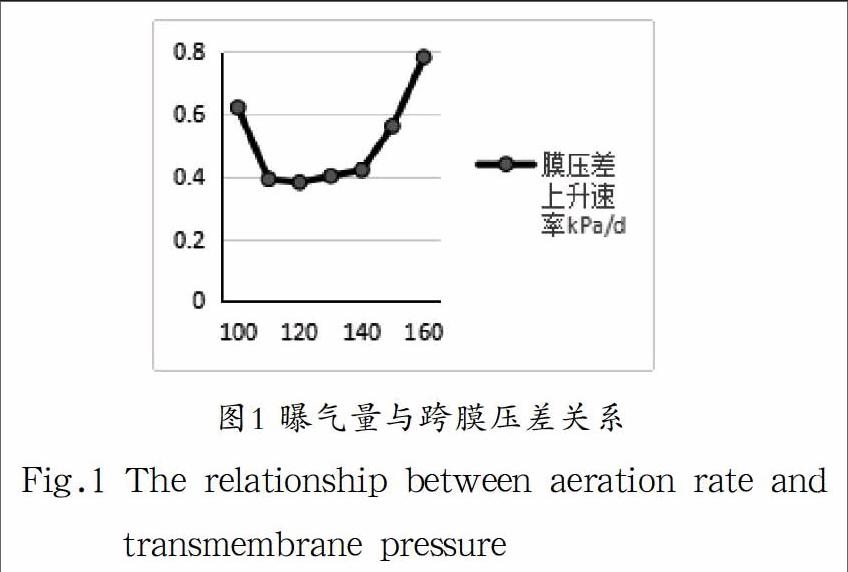
最佳曝气强度值的确定需要从生物需要量和控制膜污染两方面考虑，本研究主要从控制膜污染方面考虑。其中在保持MBR运行中恒膜通量出水的前提下以跨膜压差的变化率的大小反应膜污染的程度[7]。如在维持最佳污泥浓度操作压力为的条件下，采用中空纤维膜管式组件，首先检测放入MBR池中的新膜组件在不同的曝气量下，跨膜压差（TMP）的变化来确定最佳曝气量，曝气量试验分别选择90、110、120、130、140、150、160，以每平方米膜投影面积每小时需要的气量计算曝气量。对上述七组实验每天记录膜组件跨膜压差的值，当跨膜压差达到0.04MPa时停止试验，因为此时膜堵塞非常严重。在膜通量恒定的情况下，跨膜压差（TMP）的变化可以反映出膜污染的情况[8]。曝气量与跨膜压差上升速率的关系，如图1所示。

由图可见，曝气量强度过低或过高都会加速膜污染。因此实验中膜组件在第一个阶段最佳的曝气量强度应选择。相同的方法记录下清洗次数为0-10次后的最佳曝气强度值依次为：120、121、122、125、127、129、132、133、135、138、142 。

3 灰色系统和神经网络理论（Grey system and neural network theory）

3.1 GM（1，1）灰色系统的基本原理

GM（1，1）算法已广泛应用于社会、经济、生态、工程预测控制等领域。因适应贫信息，抗噪声能力强。显示出比传统预测方法更大的优越性。该算法的基本思想是：将原始信息数据序列通过一定的数学方法进行处理，通常采用累加或累减生成方法，转化为微分方程来描述系统的客观规律。灰色系统预测是一种通过原始数据的处理和灰色模型的建立，发现、掌握系统发展规律，对系统的未来状态做出科学的定量预测。能够较好的预测变化的总体趋势。

传统的灰预测模型GM（1，1）为等间距灰序列的预测算法。其反映了一个变量对时间的一阶微分函数，其相应的微分方程为

3.2 BP神经网络预测模型原理

BP网络是一种按误差逆向传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。能够学习和存储大量的输入—输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。

BP神经网络的学习状态是有导师的学习，其算法是将一组训练集（training set）送入网络，根据网络的实际输出与期望输出间的差别来调整连接权。有导师学习算法的主要步骤包括：

（1）从样本集合中取一个样本（Ai，Bi）。

（2）计算网络的实际输出O。

（3）求D=Bi-O。

（4）根据D调整权矩阵W。

（5）每个样本重复上述过程，直到对整个样本集来说，误差不超过规定范围。

BP网络算法的流程图，如图2所示。

3.3 灰色神经网络预测模型原理

灰色神经网络既是灰色理论与神经网络的组合，其组合方法有并联型灰色神经网络和串联型灰色神经网络两种模型。并联灰色神经网络是单项模型的线性加权和，没有考虑到单项模型预测结果之间的非线性关系。串联型灰色神经网络只将灰色预测模型的预测结果作为输入，忽略了其他影响因素对预测结果的影响。基于此，采用改进的串联灰色神经网络，如图3所示。将灰色模型的预测结果和影响曝气量的其他因素作为BP神经网络的输入，通过训练神经网络，实现预测值与实测值的最佳拟合。

4 最佳曝气预测模型的建立

把实验测得的最佳曝气强度值作为预测模型的初始数据输入，分别进行灰色系统预测和灰色神经网络预测。

4.1 最佳曝气GM（1，1）灰色预测的建立

灰色系统理论在建模过程中利用较少的数据就能得到一定精度的模拟数据，将膜清洗次数分别为0—2次所对应的最佳曝气强度的值作为GM（1，1）模型的初始输入值，进行预测膜清洗3—10次所对应的最佳曝气强度的值。如图4所示。

4.2 最佳曝气BP神经网络预测模型的建立

由于BP神经网络能够使得多元函数进行非线性的拟合并预测，本模型将影响膜过滤性能的因素膜清洗的次数、膜清洗时长、膜清洗药剂浓度作为输入，输出为最佳曝气强度值。简单的BP神经网络预测曝气强度值模型图，如图5所示。

4.3 最佳曝气灰色神经网络预测模型的建立

将实验获得的膜清洗次数大于两次的实验数据作为最佳曝气强度灰色神经网络组合预测模型的输入，其中数据包括灰色系统预测的结果值和影响膜过滤状态再而导致曝气强度值的膜清洗次数、膜清洗时长、膜清洗药剂浓度。此模型的结果输出为最佳曝气强度值。图6为最佳曝气强度灰色神经网络组合模型图。

5 结果分析（Result analysis）

我们将MBR实验获得的膜清洗次数、膜清洗时长、膜清洗药剂浓度、最佳曝气强度等数据用于上述灰色系统、BP神经网络模型、灰色神经网络模型进行计算机仿真预测。

5.1 GM（1，1）灰色预测结果分析

将MBR实验获得膜清洗0—2次所对应的最佳曝气强度值作为灰色系统的输入，通过MATLAB程序实现对膜清洗3—10次后所对应最佳曝气强度值。预测的结果，如图7所示。

通过此灰色系统模型预测的结果分析，可以看出预测的膜清洗3—10次后所对应的最佳曝气量的结果与实测结果存在较大的误差。主要原因是因为灰色系统预测模型的输入比较单一，没有考虑到膜的过滤性能恢复程度受到多种因素的影响。因此，GM（1，1）灰色系统预测模型只能是预测最佳曝气强度值随膜清洗次数的一个总的变化趋势。对于精准预测各个阶段的最佳曝气强度值存在较大的误差。

5.2 BP神经网络预测结果分析

通过MBR实验获得90组关于膜清洗次数、膜清洗时长、膜清洗药剂浓度、最佳曝气量的数据，随机选其中80组作为BP神经网络的输入，进行网络训练，建立网络模型，再将剩下的10组作为该模型的测试数据输入进行测试。通过MATALB程序实现结果，如图8所示。

通过BP神经网络模型预测结果分析，可知BP神经网络识别的正确率为80%。

5.3 灰色神经网络预测结果分析

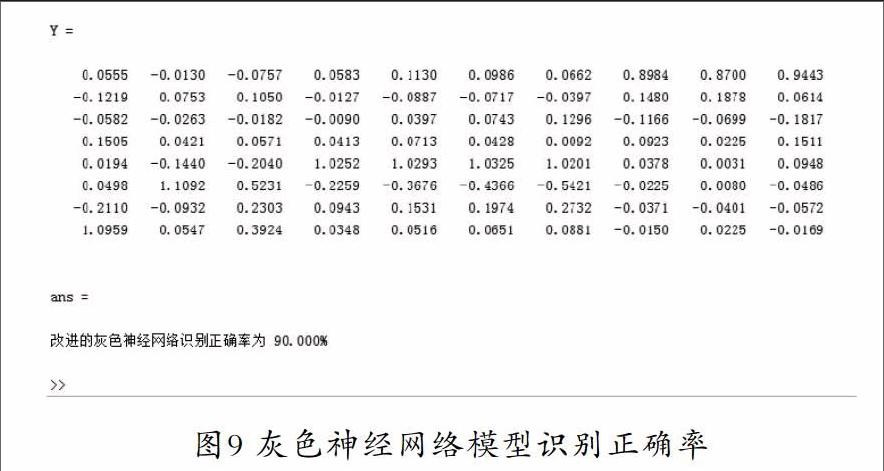
将MBR中获得的90组数据中，对应相应的膜清洗次数添加灰色系统预测的结果，从而也将灰色系统预测的结果作为灰色神经网络的输入，接着进行网络训练，建立灰色神经网络预测模型。使用同样的10组添加了灰色系统预测结果的数据作为该模型的测试数据，进行该灰色神经网络的测试。通过MATALB程序实现结果，如图9所示。

通过灰色神经网络模型预测结果分析，可知灰色神经网络模型识别正确率为90%。

6 结论（Conclusion）

本文在查阅了大量的关于MBR中膜污染相关的国内外文献后，先得出最佳曝气强度值受到膜清洗次数、膜清洗时长、膜清洗药剂等影响的理论知识，并进行相应的MBR实验研究得出相应的实验数据。再结合数学模型和计算机中的神经网络算法对求得的最佳曝气强度值进行模拟仿真。通过简单的BP神经预测模型和灰色神经网络组合预测模型的正确识别率进行对比分析，可知组合的灰色神经网络模型能够更加精确的预测出膜清洗后的下一使用阶段的最佳曝气强度值。

参考文献（References）

[1] Shibam Mitra，Naphtali Claude Daltrophe，Jack Gilron. A Novel Eductor-Based MBR for the Treatment of Domestic Wastewater[J].Water Research，2016，100：65-79.

[2] Shamim Ahmed Deowan，Francesco Galiano，Jan Hoinkis，Daniel Johnson，Sacide Alsoy Altinkaya，Bartolo Gabriele，Nidal Hilal，Enrico Drioli，Alberto Figoli.Novel Low-Fouling Membrane Bioreactor （MBR） for Industrial Wastewater Treatment[J].Journal of Membrane Science，2016，510：524-532.

[3] Young Suk Kim，Byoung Ho Lee.Fouling Reduction Effect in MBR System by Ozone Injection[J].KSCE Journal of Civil Engineering，2014，18（2）：462-469.

[4] 李朝阳，魏毅.基于MATLAB灰色GM（1，1）模型的大气污染物浓度预测[J].环境科学与管理，2012，01：48-53.

[5] 黄丽.BP神经网络算法改进及应用研究[D].重庆师范大学，2008.

[6] 王运超，等.MBR动态曝气及其在膜污染控制中的应用研究[J].水处理技术，2016，02：92-95；99.

[7] 孟凡刚.膜生物反应器膜污染行为的识别与表征[D].大连理工大学，2007.

[8] 刘晨光.膜生物反应器运行中膜污染控制对策的研究[D].天津大学，2005.

作者简介：

史亚威（1991-）， 男， 硕士生.研究领域：MBR计算机模拟仿真，大数据与云计算

李春青（1962-）， 男，博士， 教授.研究领域：MBR计算机模拟仿真，大数据与云计算.