设计-施工承包模式下单层球面网壳的优化

吴夏燕，肖建春，罗 杰，余金坤，马克俭

(贵州大学 空间结构研究中心，贵州 贵阳 550003)

设计-施工承包模式下单层球面网壳的优化

吴夏燕，肖建春*，罗 杰，余金坤，马克俭

(贵州大学 空间结构研究中心，贵州 贵阳 550003)

设计-施工承包模式下单层球面网壳的优化不只是一个降低用钢量的问题。采用均匀迭代设计法进行该模式下单层球面网壳的优化设计。采用杆件截面类型数近似代替项目工期、施工的设备条件、施工人员的素质、施工难度、管理费等因素。通过简化，以满足位移、应力、稳定性条件的网壳用钢量最轻和杆件截面类型数最少为目标。以60m跨凯威特型单层球面网壳的优化设计为算例说明该方法的运算过程。该方法减少了试验次数，收敛速度快。

DB模式；单层球面网壳；迭代均匀设计；结构优化

设计-施工(Design and Build，即DB)承包模式是由承包人提供设计和施工服务，对工程全过程的造价、工期、质量负责的一种项目承包模式。这种模式减少了业主的责任、义务和风险。

已有学者对单层球面网壳的优化做了大量工作。文[1]考虑了位移、应力和杆件稳定以及结构整体稳定性条件,对凯威特型单层球面网壳进行了截面优化设计。文[2]以位移和应力为约束，考虑结构几何非线性的影响，以杆件自重最轻为目标函数对单层网壳进行了优化。文[3]提出了一种改进的遗传算法，对某单层网壳进行了杆件截面优化设计。目前对于单层球面网壳的优化设计多为杆件截面优化设计，以杆件自重最轻为目标函数，没有考虑到项目工期、施工的设备条件、施工人员的素质、施工难度、管理费等因素的影响，不符合DB模式实际情况。

使用均匀迭代设计法进行DB模式下单层球面网壳的优化。通过因素关联分析，提出采用杆件截面类型数近似代替项目工期、施工的设备条件、施工人员的素质、施工难度、管理费等因素。在满足位移、应力、稳定性条件下，以网壳用钢量最轻和杆件截面类型数最少为目标进行DB模式下单层球面网壳的优化设计。

1 迭代均匀设计法

迭代均匀设计方法即在均匀试验设计方法的基础上增加迭代步骤的设计方法。文[4]等采用均匀设计法进行预应力局部单双层扁网壳结构的参数分析与近似优化，得到了比较理想的最优水平组合。均匀试验设计方法[5]具有试验点均匀分布的特点，但由于试验点数量有限，均匀设计不一定能实现凸集规划，往往第一次均匀设计的结果不能满足实际应用中的优化设计要求。在均匀试验设计的基础上，增加迭代步骤，能快速结果的收敛，实现凸集规划。具体叙述如下：

通过均匀试验设计以及回归分析即可得出目标与变量之间的函数关系，并能通过数学软件求解出一定约束条件下的第一次最优组合。以第1次最优组合为基础，定出新的水平数，确定均匀设计表进行试验，回归分析考虑前次试验的数据，使规划趋于凸集规划。第2次最优组合必定会比第1次最优组合更加接近全局最优组合。假定第2次最优组合就是全局最优组合，对第1、2最优组合进行比较，若小于给定的一个允许误差，就认为第2次最优组合是真正的全局最优组合；若大于给定的允许误差ε，就认为第2次最优组合不是真正的全局最优组合，需要继续进行迭代均匀设计，直到第n、n+1次最优组合间的误差小于ε，就可停止迭代。由于优化变量可能是离散变量，ε在迭代过程中会出现跳跃现象，此时若组合间的误差小于ε说明真正的全局最优解在两者之间，仍可以停止迭代，而以目标函数极值最小的一个为全局最优解，与之相对应的组合为全局最优组合。

2 DB模式下单层球面网壳的优化实例分析

2.1 目标函数

网壳结构中节点数量多，节点用钢量大，考虑杆件用钢量的同时也应考虑节点用钢量。一般来说，减少构件种类可以降低运输及管理成本。同时，杆件截面类型越少,则加工、安装越简便，运输费、管理费越低。加之减少杆件截面类型数对缩短工期也有利。这里为了简化，用杆件截面类型数近似代替项目工期、施工的设备条件、施工人员的素质、施工难度、管理费等指标。以总用钢量(包括杆件用钢量和节点用钢量)最低和杆件截面类型数最少优化目标更贴近实际。由于各目标之间量纲不同，通过各目标值与初始设计中对应值的比值最小作为新的子目标。最后以所有子目标的权函数作为优化模型的最终目标。

(1)总用钢量与初始设计总用钢量比值最小。

(1)

(2)杆件截面类型数与初始设计杆件截面类型数比值最小。

F2=min[N/N*]

(2)

总目标函数为：

F=min[αF1+βF2]

(3)

式中：Ai为第i根杆件的截面面积，li为第i根杆件的长度，ρi为第i根杆件的密度，Ci为第i个球

节点的重量，G*为初始设计中杆件用钢量与球节点用钢量重量之和。N为杆件截面类型数，N*为初始设计中杆件截面类型数。α、β分别为各子目标权重，根据不同项目和业主意向确定。

2.2 算例说明

以跨度L=60m的凯威特型单层球面网壳为例分析。选取网壳矢高h、环向网格数a、径向网格数b为分析变量。支承方式为周边铰接，支座对称布置。典型计算模型见图1。

荷载情况：恒荷载标准值1.0kN/m2,活荷载标准值0.5kN/m2,基本风压-0.5kN/m2,不考虑雪荷载和地震作用。考虑四种荷载组合情况：(1)1.2恒；(2)1.2恒+1.4风；(3)1.2恒+1.4活；(4)1.2恒+1.4活+0.8风。

采用专业设计软件MSTcad进行满应力设计，选取统一的杆件材料库，节点采用焊接球节点。本例球节点总用钢量取杆件总用钢量的15%[6]。极限承载力计算采用ANSYS进行弹性全过程分析，λ为极限承载力系数，单层球面网壳取4.2[7]，1.0恒载+1.0活载作用时λ=1。初始设计参数如表1，其中G为杆件用钢量，Wmax为网壳最大位移。

图1 凯威特型网壳示意图

h/mabG/tG∗/tWmax/mmN∗λ148631．3461．15∗31．34618．675．3767

2.3 迭代均匀设计优化过程

第一次均匀试验参数水平如表2，选取运行次数是设计水平数3倍的均匀设计表U15(53),其CD2偏差是0.013149。试验方案及结果见表3。

表2 第一次均匀试验设计参数水平表

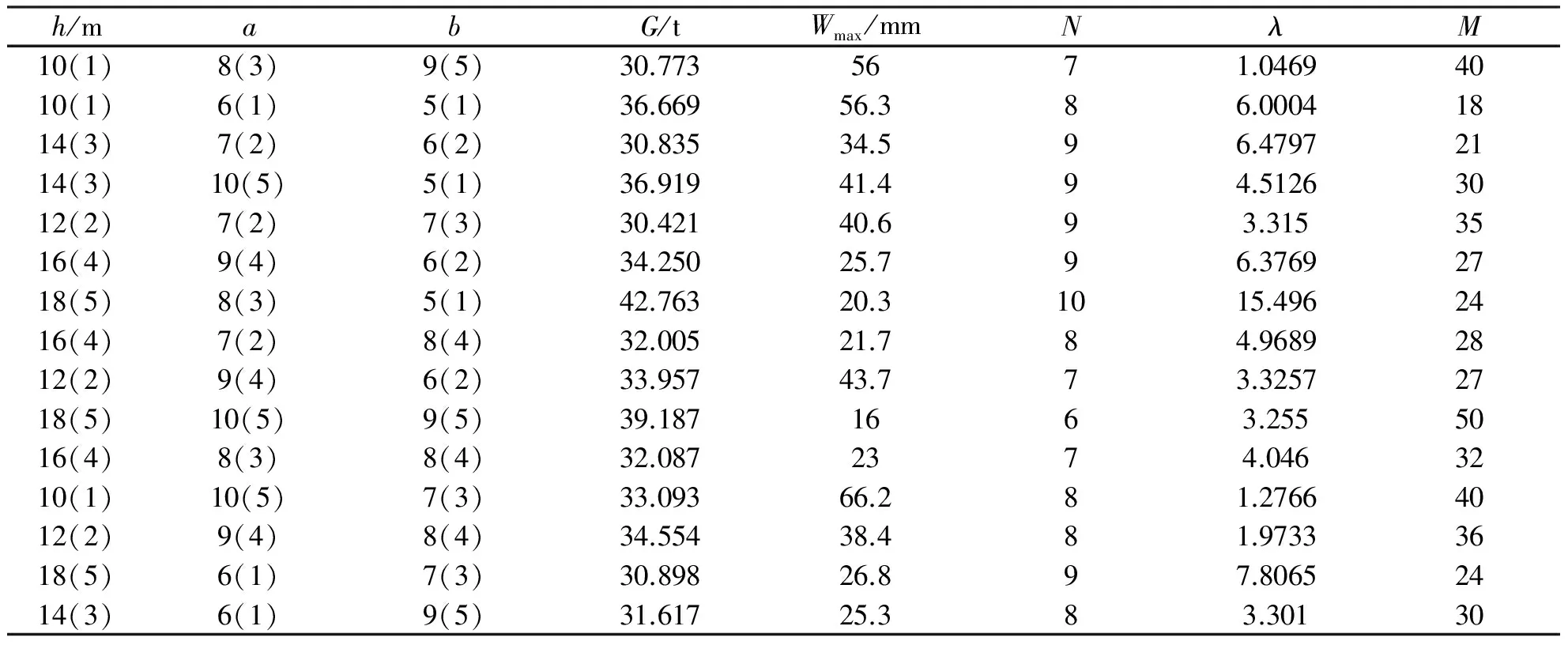
表3 第一次均匀试验方案及结果

利用Origin软件对表3数据进行回归分析，得到下列近似函数关系：

(1)杆件用钢量G，

G=231.58392+22.31929h-37.43227a-80.43151b

-1.75736h2+4.7069a2+10.40767b2+0.07652ha

+0.01594hb+0.15233ab+0.04417h3-0.1999a3

-0.44999b3

(5)

(2)杆件截面类型数N，

N=7.43741+2.16551h+3.81802a-8.55788b

-0.02689h2-1.26605a2+2.05912b2+0.11704ha

-0.28688hb+0.06742ab-0.00042631h3+0.07225a3

-0.11452b3

(6)

(3)网壳最大位移Wmax，

Wmax=-29.49558-53.85421h+103.59154a+49.9563b+3.4569h2-13.09809a2-7.32658b2-0.56272ha-0.08884hb+0.05373ab-0.07057h3+0.58544a3

+0.34239b3

(7)

λ=0.04143+6.93736h+7.18106a-17.94972b

-0.37519h2-0.8284a2+2.05912b2-0.07167ha-0.18994hb+0.23052ab+0.01032h3+0.02444a3

-0.07669b3

(8)

本例取各子目标权重为α=1，β=1，则近似目标函数为：

=8.214368425+0.952642146h-0.769939723a-3.516801352b-0.059051071h2+0.009487288a2+0.560816569b2+0.015445585ha-0.031367038hb

+0.012350742ab+0.001361743h3+0.001650569a3

-0.027080024b3

(9)

最优水平组合问题归结为下列数学条件极值问题：

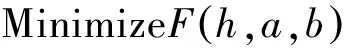
(10)

其中约束条件Wmax、λ根据《空间网格结构技术规程》(JGJ 7-2010)确定，L为网壳跨度。利用Matlab软件求解该极值问题得到第一次均匀试验近似最优解h=18.7427，a=7，b=9，F=1.47978。取允许误差ε为1%。

第一次迭代均匀试验设计方案见表4，计算给出4组试验结果，结合第一次均匀试验设计的数据共19组数据，拟合出新的回归方程，求解出近似最优解为h=22.3932，a=6，b=10，F=1.5309。与第一次均匀试验最优解比较，误差为3.45%，继续迭代。第二次迭代均匀试验设计方案见表5，结合前两次均匀试验共23组数据，拟合出新的方程，解得近似最优解为h=19.4804，a=8，b=11，F=1.55732。与第一次迭代均匀试验最优解比较，误差为1.73%，继续迭代。第三次迭代均匀试验设计方案见表6，结合前三次均匀试验共27组数据，拟合出新的方程，解得近似最优解为h=17.9463，a=8，b=12，F=1.54345。比较第三次迭代结果和第二次迭代结果，误差为0.89%，认为迭代收敛，取第三次迭代结果为最优组合即h=17.9463，a=8，b=12，F=1.54345。可以看出迭代均匀试验设计方法减少了试验点的设计和试验次数的进行，加快了结果收敛速度，高效快速地给出了理想的设计方案。

表4 第一次迭代均匀试验设计方案表

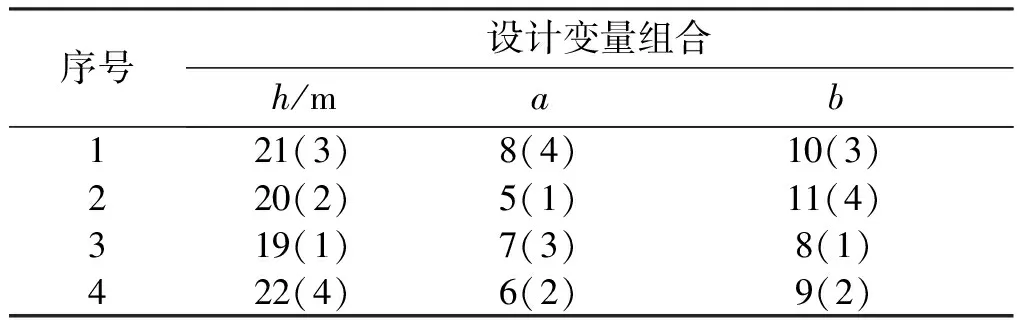
表5 第二次迭代均匀试验设计方案表

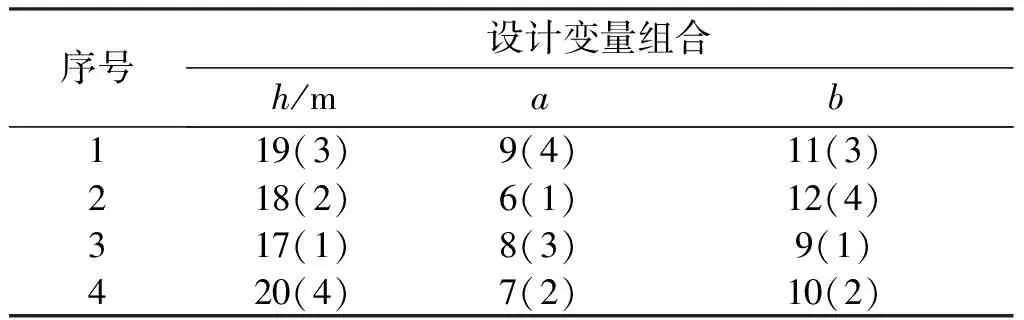
表6 第三次迭代均匀试验设计方案表

3 总结

DB模式下单层球面网壳的优化不只是一个降低用钢量的问题，还应该考虑项目工期、施工的设备条件、施工人员的素质、施工难度、管理费等因素的影响。提出更符合实际的用杆件截面类型数近似考虑项目工期、施工的设备条件、施工人员的素质、施工难度、管理费等指标，以网壳用钢量最低和杆件截面类型数最少为目标的迭代均匀试验设计方法进行网壳的优化。该方法将多量纲多目标优化问题转化为无量纲单目标优化问题，将各目标值与初始设计对应值之比作为子目标，最后根据各子目标权重得出最终目标。

以60m跨凯威特型单层球面网壳的优化设计为算例说明该方法的运算过程。该方法减少了试验次数，收敛速度快。

[1] 王法武，唐敢. 考虑整体稳定的单层网壳截面优化设计[J]. 空间结构. 2006, 12(3): 31-34.

[2] 张年文，董石磷，黄业飞等. 考虑几何非线性影响的单层网壳优化设计[J]. 空间结构. 2003, 9(1): 31-34.

[3] 牟在根，梁杰，隋军等. 基于小生境遗传算法的单层网壳结构优化设计研究[J]. 建筑结构学报. 2006, 27(2): 115-119.

[4] 肖建春，曹新明，马星等. 预应力局部单双层扁网壳的参数分析与近似优化[J]. 建筑结构学报. 2006, 27(1): 117-123.

[5] 方开泰. 均匀设计与均匀设计表[M]. 北京: 科学出版社, 1994.

[6] 徐菁，杨松森，刁延松. 单层球面网壳的优化设计[J]. 空间结构. 2006, 12(3): 35-37.

[7] JGJ 7-2010. 空间网格结构技术规程[S]. 北京: 中国建筑工业出版社，2010.

(责任编辑：王先桃)

Optimization Design Of Single-layer Spherical Reticulated Shell under Design-build Mode

WU Xiayan，XIAO Jianchun*，LUO Jie，YU Jingkun，MA Kejian

(Space Structures Research Center, Guizhou University, Guiyang 550003, China)

The optimization design of single layer spherical reticulated shell under DB mode is not only to reduce the amount of steel. The optimization of single layer spherical reticulated shell was carried out by the uniform iterative design method in this mode. The type number of bar cross section was used to approximate the project duration, the construction of equipment conditions, the quality of construction personnel, construction difficulty and management fees. By simplifying, the objective function is to satisfy the displacement, stress and stability conditions of the minimum number of bar cross section types and the minimum steel consumption. Taking the optimum design of a 60 m span Kiewitt single-layer spherical reticulated shell as an example the operation of the method was illustrated. This method reduces the number of tests, and the convergence rate is fast.

DB mode; single layer spherical reticulated shell; iterative uniform design; structure optimization

1000-5269(2016)06-0059-04

10.15958/j.cnki.gdxbzrb.2016.06.14

2016-06-25

国家自然科学基金(50978064/080502)

吴夏燕(1991-)，女，在读硕士，研究方向：空间钢结构及组合结构，Email：875911610@qq.com.

*通讯作者： 消建春，Email：jcxiou@gzu.edu.cn.

TU357

A