上下肋对蜂窝形钢筋混凝土空腹夹层板挠度影响分析
2017-01-17徐金涛马克俭王泽曦许文柳冯献慧
徐金涛,马克俭, 才 琪,王泽曦,许文柳,冯献慧
(贵州大学 空间结构研究中心,贵州 贵阳 550003)
上下肋对蜂窝形钢筋混凝土空腹夹层板挠度影响分析
徐金涛,马克俭*, 才 琪,王泽曦,许文柳,冯献慧
(贵州大学 空间结构研究中心,贵州 贵阳 550003)
为了研究蜂窝形钢筋混凝土空腹夹层板上下肋对其挠度的影响,运用有限元软件Midas建立了某大跨度楼盖模型, 计算出不同上下肋尺寸下楼盖的挠度,对挠度曲线进行拟合,得到了挠度与肋高、肋宽的关系式。研究结果表明,蜂窝形钢筋混凝土空腹夹层板的挠度与肋高、肋宽均呈指数关系,且随着肋高和肋宽的增大而减小。肋高比肋宽对结构的挠度影响更显著。
蜂窝型;空腹夹层板;上下肋;挠度
蜂窝形空腹夹层板是一种新型的大跨度楼盖结构形式,它造型美观,具有良好的空间力学性能,当作为大跨度楼盖时其单位面积用钢量大大低于网架和网壳结构,有利于资源的节约。文献[1]研究了钢筋混凝土蜂窝形空腹夹层板的基本力学性能,并将蜂窝形空腹夹层板与常规结构进行了对比,证明了空腹夹层板相比常规结构具有很好的经济性。文献[2]研究了蜂窝形空腹夹层板的自振性能,分析了表层混凝土板厚度等参数对结构自振频率的影响。文献[3]研究了蜂窝形空腹夹层板的刚度,对蜂窝形钢空腹夹层板的屈曲模态进行了分析。在这些研究的基础上,本文重点研究上下肋截面尺寸对蜂窝形钢筋混凝土空腹夹层板挠度的影响,分析了结构挠度随肋高和肋宽的变化规律。
1 蜂窝形钢筋混凝土空腹夹层板挠度影响因素
蜂窝形钢筋混凝土空腹夹层板由上层混凝土板、上肋、剪力键和下肋组成,节点构造如图1所示。上肋层布置如图3所示,在网格划分比较大的情况下,上肋层需加设分割梁,下肋层如图4所示,上下肋由剪力键连接。蜂窝型钢筋混凝土空腹夹层板的剪力键为Y字形,图2为宽度400mm的剪力键图,面积为0.37m2,常规的空腹夹层板同样肋宽时剪力键截面面积在0.16m2左右,在相同肋宽条件下Y字形剪力键宽度更大。空腹夹层板要求剪力键宽度大于高度,Y字形剪力键可以在更小的肋宽时满足该要求,因此,蜂窝形空腹夹层板肋宽构造宽度比常规空腹夹层板小。空腹夹层板的的挠度与上下表层的薄膜刚度以及夹心层的剪切刚度有关[6],取决于均布荷载、弹性模量、跨度、边界条件、泊松比、上层混凝土板厚度、上下肋和剪力键尺寸以及空腹夹层板总高度。工程实践中Y字形剪力键的肢宽与上下肋宽度取值相同,因此,本研究模型中肋宽和Y字形剪力键肢宽是同步变化的。

h-肋高;b-肋宽;1-上层混凝土板; 2-上肋;3-下肋;4-剪力键图1 蜂窝型空腹夹层板节点图
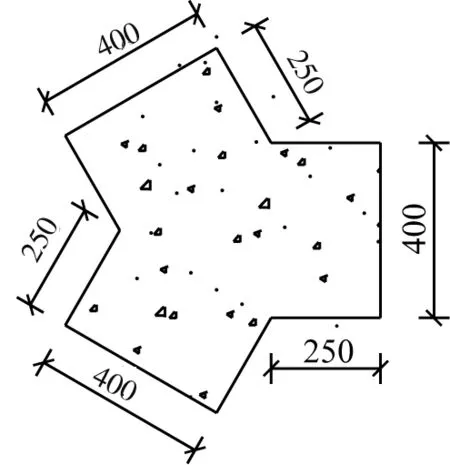
图2 剪力键图

图3 蜂窝型空腹夹层板上肋的布置
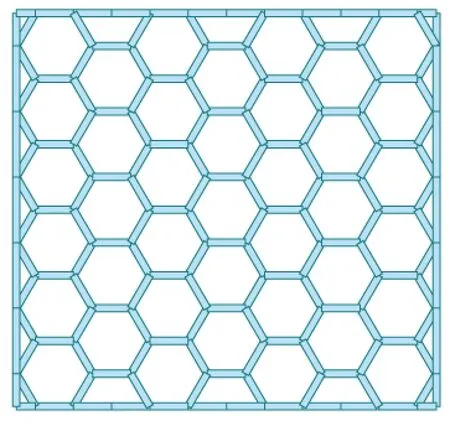
图4 蜂窝型空腹夹层板下肋布置
2 有限元模型
蜂窝形空腹夹层板模型平面尺寸为23.25m×21.96m,正六变形的边长为2.114m,现浇混凝土板厚为80mm,空腹夹层板的总高度为900mm,上层的分割梁尺寸为250mm×200mm,混凝土强度为C35,泊松比为0.2,密度2548kg/m3,Ec=31311MPa,楼面抹灰和吊顶荷载取2kN/m2,活荷载取3.5kN/m2,自重由软件计算。采用Midas 进行结构计算,本文的上下肋和剪力键采用的是梁单元,上层混凝土板采用三节点板单元,基本组成单元与周边交接处设置500mm×500mm的混凝土柱,形成支撑。
3 计算结果分析
3.1 肋宽对楼板挠度的影响
在分析肋宽对蜂窝形钢筋混凝土空腹夹层板挠度的影响时,首先将模型上下肋尺寸设置为400mm×250mm,计算得出模型的挠度为43.69mm,为板跨的1/503,满足规范小于1/300板跨的要求,然后将肋宽每次递减10mm,依次从400mm变化到300mm,计算出相应的楼板挠度。将肋高调整为240mm、230mm、220mm、210mm,计算不同宽度下的挠度值,结果如图5所示。
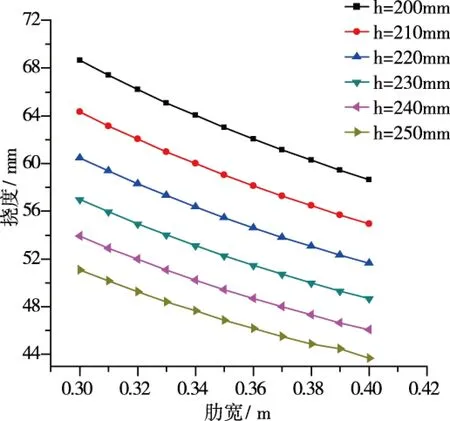
图5 肋宽—挠度曲线
3.2 肋宽—挠度曲线拟合
从肋宽-挠度曲线可以知道模型挠度随肋宽变化的规律相近,选择h=200mm的情况进行函数拟合,结果如图6所示。
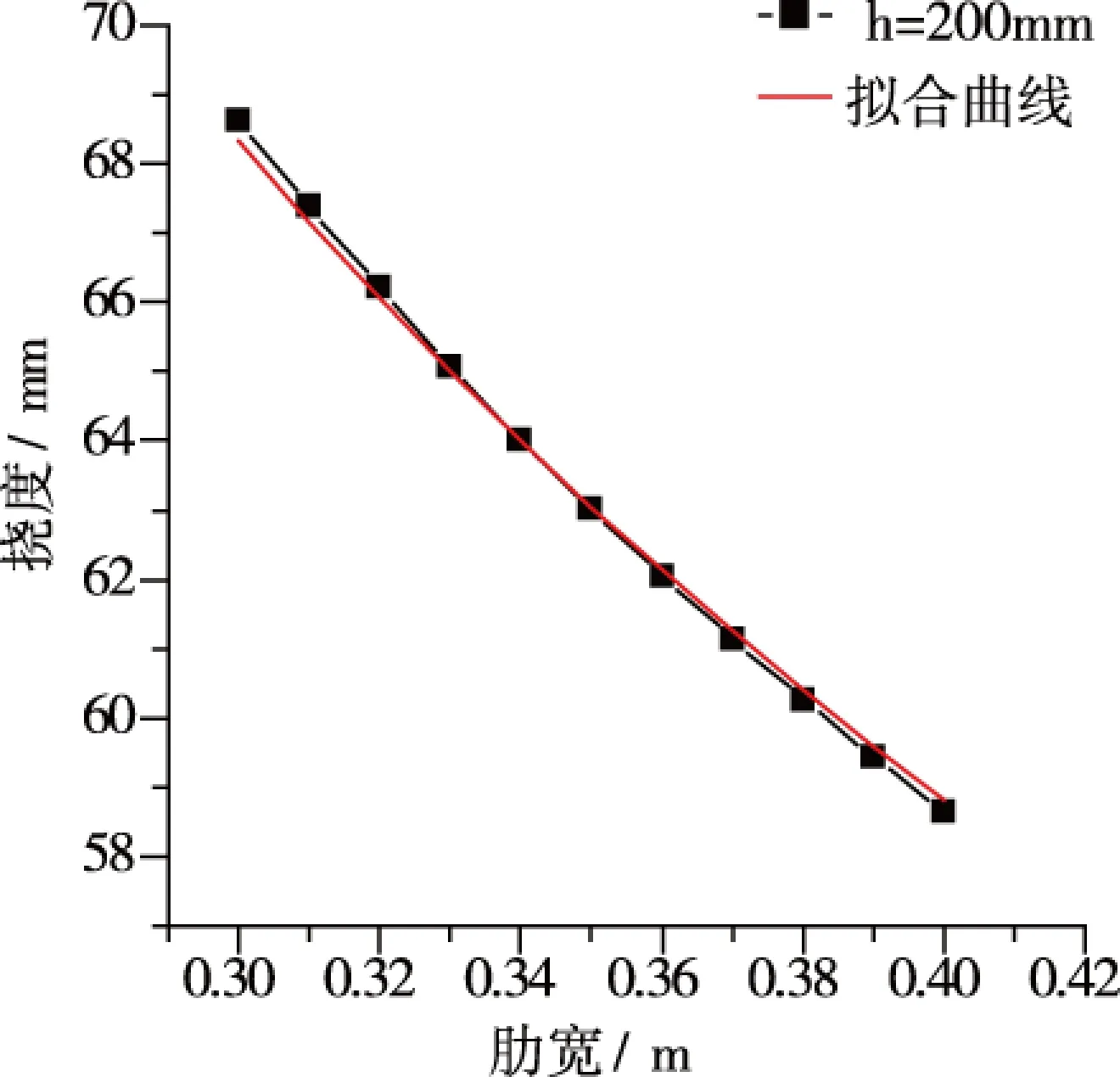
图6 肋宽—挠度拟合图
拟合的挠度计算公式为ω=34.07b-0.52,拟合公式计算挠度与软件计算挠度误差分析结果如表1所示。
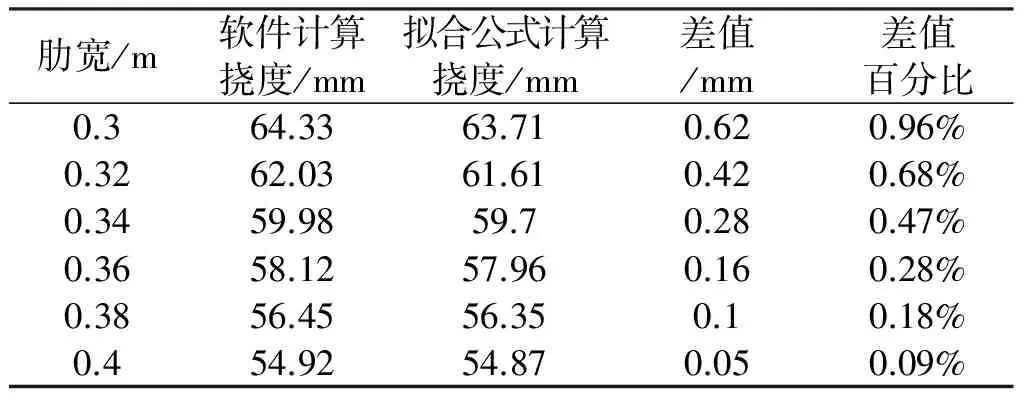
表1 肋宽—挠度拟合误差分析
从表1中可以看到,软件计算的挠度和公式计算出的挠度最大相差0.96%,这表明采用公式ω=34.07b-0.52计算的挠度与软件计算的挠度基本吻合,可以认为空腹夹层板的挠度与肋宽成指数关系,考虑到其它影响蜂窝形空腹夹层板挠度的因素,可以引进系数κ,那么蜂窝形钢筋混凝土空腹夹层板挠度和肋宽的关系可以表达为:
ω=κb-0.52
(1)
式中系数κ由肋宽以外的挠度影响因素决定。
3.3 肋宽挠度拟合公式的验证
在Midas中建立了平面尺寸为29.6m×25.62m的蜂窝形钢筋混凝土空腹夹层板模型,模型高度取1.05m,选取不同于原模型的高度,可以说明不同板高均适用肋宽与挠度的拟合关系式。在该跨度下250mm的肋高值比较合适,肋宽一次从300mm变为32mm、340mm、360mm、380mm、400mm,楼板挠度计算结果见表2。为了验证公式ω=κb-0.52,首先可以确定系数κ,将模型肋宽b=250mm该公式,可得κ=42.66,分别用Midas和公式ω=42.66b-0.52计算出不同肋宽时的楼板挠度值,并将两者进行比较,结果如表2所示。
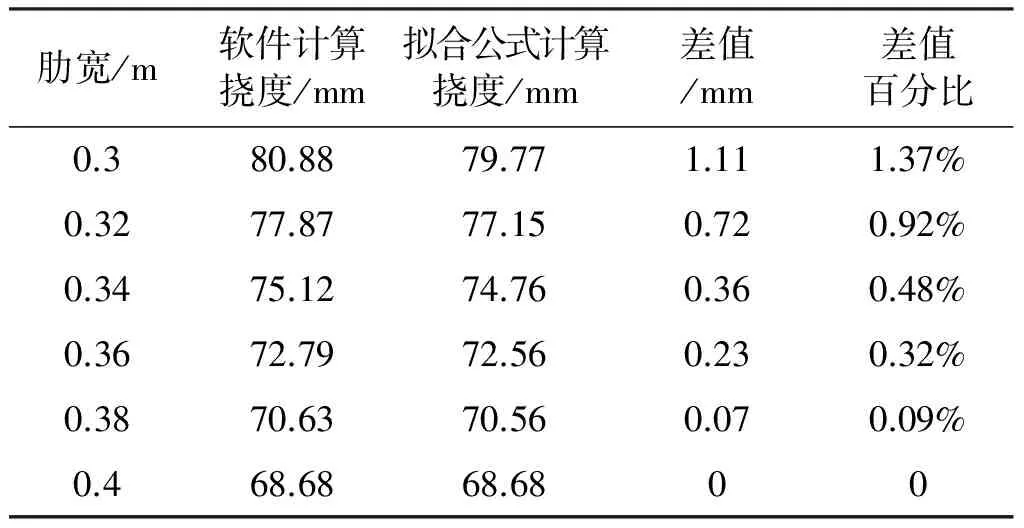
表2 肋宽—挠度拟合验证误差分析
从表2中可以看出,公式计算结果与软件计算结果最大差值1.1mm,最大差值百分比为1.37%,表明公式计算结果和有限元软件计算的挠度结果基本吻合,拟合计算公式可以认为能够正确表示挠度随肋宽变化的关系,而且该关系式在模型高度下同样适用。蜂窝形钢筋混凝土空腹夹层板的挠度与肋宽的-0.52次方成比例,这说明蜂窝形钢筋混凝土空腹夹层板的挠度与肋宽反方向变化,肋宽的增加使蜂窝形钢筋混凝土空腹夹层板挠度减小。由弹性薄板挠度方程可以知道,在荷载一定的情况下,板的挠度与板的竖向刚度反向相关,肋宽和挠度的关系式说明肋宽增大时蜂窝形钢筋混凝土空腹夹层板竖向刚度也随之增大,肋宽对竖向刚度的影响很显著。
3.4 肋高对楼板挠度的影响
为了分析肋高对钢筋混凝土空腹夹层板挠度的影响,首先将模型上下肋尺寸设置为400mm×200mm,计算出模型的挠度为58.64mm,为板跨的1/374,满足规范小于1/300板跨的要求,可以认为尺寸在合理范围,然后让肋高每次增大20mm,依次从200mm变化到300mm,分别算出相应的模型挠度,可以得到肋肋宽400mm条件下的一组楼板挠度值。用同样的方法得到390mm、380mm、370mm、360mm的肋宽条件下的楼板挠度值,结果如图7所示。
3.5 肋高—挠度曲线的拟合
各肋宽条件下的曲线变化规律相似,将b=400mm的曲线进行拟合,拟合的结果如图8所示。
拟合得到挠度计算公式,公式为ω=9.32h-1.12,拟合误差见表3。
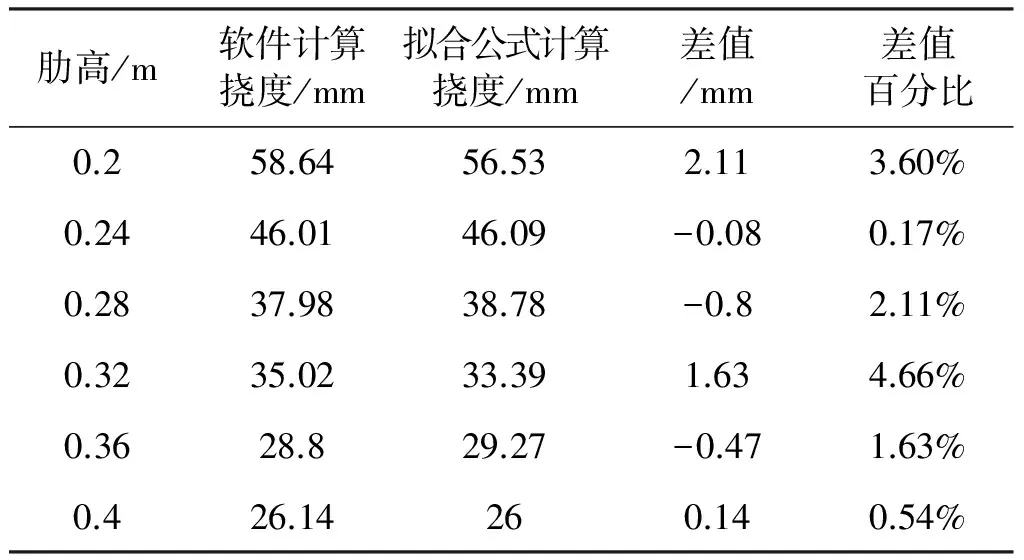
表3 肋高—挠度拟合误差分析
从拟合误差分析表中可以看到,软件计算的挠度和公式计算的挠度值最大相差4.66%,这表明采用公式ω=9.32h-1.12计算的挠度能够和软件的结果相吻合。拟合结果说明蜂窝型钢筋混凝土空腹夹层板挠度和肋高成指数关系:
ω=μh-1.12
(2)
式中μ由肋高以外的挠度影响因素决定。
3.6 肋高拟合公式的验证
模型与肋宽-挠度公式验证时相同,将肋宽设置为400mm,将肋高依次设置为260mm、280mm、300mm、320mm、340mm、360mm,将h=300mm带入公式ω=μh-1.12,求得系数值μ=14.54,分别用Midas个公式计算出各组肋高条件下的挠度值,并将两者进行比较,结果如表4所示。
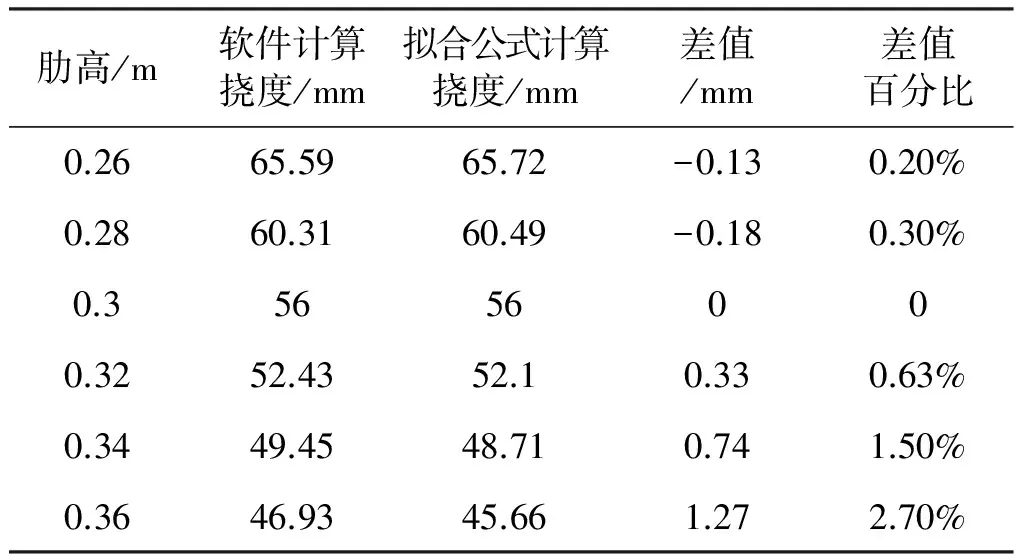
表4 肋高—挠度拟合验证误差分析
从表2中可以看出,采用拟合公式计算出的挠度和软件计算挠度最大相差1.27mm,差值的百分比不超过2.7%,表明拟合公式能够反应肋高和蜂窝形钢筋混凝土空腹夹层板挠度的关系。从拟合出的公式可以知道,蜂窝形钢筋混凝土空腹夹层板的挠度与肋高-1.12次方有关,肋高增大时蜂窝形空腹夹层板的挠度随之减小,肋高对竖向刚度的影响十分显著。
3.7 楼板挠度双参数公式验证
同时考虑肋宽和肋高对挠度的影响,可以得到以下公式:
ω=ψb-0.52h-1.12
(3)
式中b—肋宽
h—肋高
系数ψ由肋宽和肋高以外的挠度影响因素决定。为了说明肋高和肋宽同时作用时是否存在相互干扰,有必要对公式3进行验证。将上下肋尺寸设置为300mm×400mm,通过软件计算出挠度值56mm,将其公式3,可以求得ψ=9.03,验证模型的挠度计算公式为ω=9.03b-0.52h-1.12,选择280mm×380mm、300mm×360mm、320mm×400mm、340mm×380mm、360mm×400mm的上下肋截面尺寸,分别用软件和公式计算出挠度值,将两者的结果进行对比,结果如表5所示。
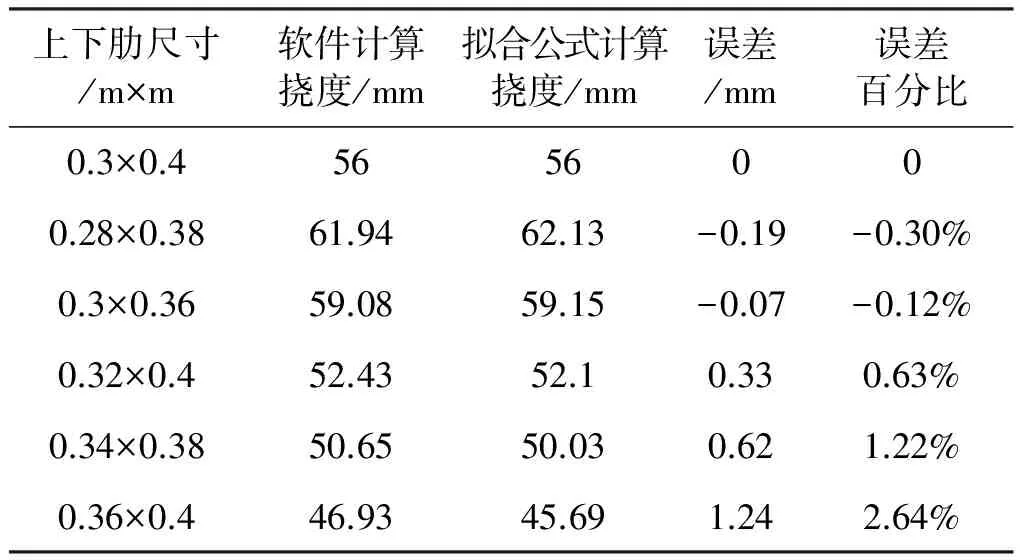
表5 楼板挠度双参数公式验证误差分析
两者最大的差值1.24mm,最大差值百分比为2.64%,这表明公式计算的挠度值和软件计算的挠度值基本一致,说明肋高和肋宽对挠度的影响互不干扰。
为了保证剪力键的力学特性,剪力键的高度大于宽度[6],选取的模型上下肋的尺寸均在构造要求的范围内,以原模型上下肋尺寸300mm×250mm为例,Y字形剪力的面积欲510mm正方形相等,剪力键高度为400mm,可以认为剪力键宽高比大于1,满足构造要求。因此公式3表明,在满足剪力键构造要求的前提下,肋高对挠度的影响比肋宽更加显著。由此可知肋高对蜂窝形钢筋混凝土的竖向刚度的影响比肋宽大,在实际工程中,可以根据构造要求确定肋宽,根据挠度要求确定肋高。
4 结论
(1)蜂窝形钢筋混凝土空腹夹层板的肋高和肋宽与挠度均呈指数关系,增大肋宽和肋高都能有效的减小蜂窝形钢筋混凝土空腹夹层板的挠度,
(2)肋宽和肋高对蜂窝形钢筋混凝土空腹夹层板挠度的影响相互独立。
(3)在满足构造要求时,肋高对蜂窝形钢筋混凝土空腹夹层板挠度的影响比肋宽更加显著,但工程实践中为保证连接上、下肋的剪力键为块体单元,即其净高与净宽之比小于或等于1,上下肋一般均采用肋宽大于肋高的截面形式。
[1] 王泽曦,马克俭,晁亚茹,等.钢筋混凝土网格蜂窝型盒式结构力学性能对比分析[J]. 贵州大学学报(自然科学版). 2016,33(2):97-101.
[2] 晁亚茹,马克俭,申波,等.蜂窝型空腹夹层板的自振特性研究[J]. 贵州大学学报(自然科学版). 2016,33(2):106-111.
[3] 才琪,马克俭,刘卓群.多层大跨度蜂窝形钢空腹夹层板楼盖刚度分析[J]. 贵州大学学报(自然科学版). 2016,33(3):106-109.
[4] 刘卓群,马克俭,肖建春,等.混凝土板对钢空腹夹层板楼盖静力性能影响分析[J]. 广西大学学报(自然科学版). 2016,41(1):1-10.
[5] 刘卓群,肖建春,陈靖,等.钢-混凝土组合空腹夹层板关键部位力学特性分析[J]. 贵州大学学报(自然科学版). 2015,32(3):119-122.
[6] 马克俭,张华刚,郑涛著.新型建筑空间网格结构理论与实践[M]. 人民交通出版社, 2006:76-119.
(责任编辑:王先桃)
Influence of Upper and Lower Ribs on the Deflection of the Honeycomb Shape Reinforced Concrete Open-web Sandwich Plate
XU Jintao, MA Kejian*, CAI Qi, WANG Zexi,XU Wenliu, FENG Xianhui
(Space Structure Research Center, Guizhou University, Guiyang 550003, China)
In order to study the honeycomb reinforced concrete open-web Sandwich Plate under the rib effect on the deflection, the finite element software Midas was used to build a large span floor model, on the floor under the rib size under the deflection fitting of the deflection curve was calculated, the relationship between the deflection and the fin height, fin width was obtained. The results show that the deflection of the honeycomb reinforced concrete hollow sandwich plate has an exponential relationship with the rib height and the rib width, and decreases with the increase of the rib height and the rib width. The effect of rib width on the deflection of the structure is more significant.
honeycomb type; open- web sandwich plate; upper and lower ribs; deflection
1000-5269(2016)06-0054-05
10.15958/j.cnki.gdxbzrb.2016.06.13
2016-08-20
国家自然科学基金项目资助(50978064/E080502);十二五国家科技支撑计划(2011BAJ09B01-01)
徐金涛(1989-),男,在读硕士,研究方向:大跨度空间结构,Email:1009941051@qq.com.
*通讯作者: 马克俭,Email:makejian2002@163.com.
TU375.2
A
