分层广义线性模型在准备金评估中的建模研究*

闫 春， 李延星， 陈祥辉， 邱艺伟

(山东科技大学 数学与系统科学学院, 山东 青岛 266590)

分层广义线性模型在准备金评估中的建模研究*

闫 春†， 李延星， 陈祥辉， 邱艺伟

(山东科技大学 数学与系统科学学院, 山东 青岛 266590)

考虑到赔付流量三角形数据同一事故年反复观测的纵向特征以及数据结构的层次性，建立了分层广义线性模型.与通常的随机模型相比，分层广义线性模型不但可以选择条件反应变量的分布而且风险参数分布范围也更加广泛.利用h-似然函数估计分层广义线性模型的模型参数，降低了计算量.为使模型具有可比性，评估模型的预测精度，推导了模型预测误差的估计式.为充分利用已知赔付信息，将赔付额和赔付次数两种赔付信息纳入未决赔款准备金评估模型，建立了两阶段分层广义线性模型.在线性预测量中考虑了各种固定效应和随机效应以及模型结构的散布参数，改进了线性预估量结构.研究表明：分层广义线性模型对于数据的各种分布及形式都具有很好的适应性，更加符合保险实务现实的赔付规律.

保险数学；分层广义线性模型；h-似然函数；预测误差

1 引 言

未决赔款准备金的评估方法是非寿险精算的重要组成部分，其评估模型的理论与实践正在经历着巨大的变革.为维护保险行业的健康发展，保监会规定了保险实务中常用的几种评估未决赔款准备金的确定性方法.但赔款额本质上是一个随机变量，确定性评估方法只能基于历史数据对未决赔款准备金进行点估计，无法得到估计误差及波动程度.在全球经济市场环境不稳定、巨额索赔风险频繁发生的情况下，引入可靠性强、能够度量准备金波动性以及模拟准备金预测分布的随机模型显得尤为重要.为了实施新的会计准则，保监会财务会计部在2010年1月举办了关于非寿险未决赔款责任准备金评估方法的系列培训，新出台的保险合同相关会计处理规定鼓励财险公司采用随机性模型与方法(如Mack模型、GLM模型、Bootstrap方法等) 评估未决赔款准备金.

但是随机性模型并非完美无瑕，仍有不少亟需完善的问题.即使经典的广义线性模型(Generalized Linear Models，GLM)仍存在不少缺陷，如对于在某些水平上数据量很少的分类解释变量GLM参数估计的标准误差会很大.对于相互独立且具有层次性结构的数据，若直接应用GLM会产生过多的待估参数.此外，GLM线性预估量仅仅包含固定效应，忽略了不同事故年赔付数据之间的异质性以及相同事故年不同进展年间赔付数据的相关性.为了克服了GLM的缺陷，有些学者引入了广义线性混合模型(Generalized Linear Mixed Models， GLMM)，该模型在线性预测部分引入了随机效应，不仅考虑了不同事故年间的互异性，还反映了同一事故年不同进展年赔付数据由于共同纵向特征而产生的组内数据的相关性.近年来GLMM在精算中的应用越来越受到国内外学者的重视，如Kelvin(2003)[1]等对索赔频率分别使用GLM和GLMM建模，通过对比分析指出了GLMM的优势.Antonio和 Beirlant( 2008)[2]基于GLMM 的半参数回归模型结合贝叶斯方法模拟了索赔准备金的预测分布.Klinker(2011)[3]进一步研究了GLMM在Buhlmann-Straub信度模型理论上的应用.谢远涛和杨娟(2014)[4]基于操作时间来重新设计流量三角形，并利用GLMM评估准备金.刘新红和孟生旺(2014)[5]对增量已决赔款建立GAMLSS模型，并将此模型应用于一组具有明显异方差的车险数据，证明拟合效果优于均值回归模型.

然而GLMM的主要缺点是随机效应必须服从正态分布，且随机效应项的引入使得边际似然函数的计算更加复杂，往往需要高阶微积分运算，算法实现具有局限性.针对GLMM的缺陷，学者们进一步将模型推广为随机效应服从指数类分布族的分层广义线性模型(Hierarchical Generalized Linear Models，HGLM).该模型的基本思想在于模型的某些参数本身需要建模，分层模型中固定效应为通过样本数据直接估计的模型参数，随机效应则是通过模型的超参数间接估计的模型参数.GLM等随机评估方法大多没有体现赔付数据随事故年反复观测的纵向特征，而HGLM作为处理纵向数据的一种自然方式，将赔付流量三角形视作分层数据，以每个事故年相应的赔付数据为一个“目标”来评估索赔准备金.近年来有关广义线性分层模型的研究不断涌现，1996年Y. Lee和J.A.Nelder[6]首次提出了HGLM的概念，并于2006[7]年对HGLM进一步推广给出了双广义线性分层模型.

随后Y. Lee和M. Noh于2012[8]年又给出了双广义线性分层模型的随机效应方差.Payne R W(2014)[9]回顾了广义非线性模型及算法，依据HGLM相关理论确定了分层广义非线性模型.HGLM通过h-似然函数来估计模型参数，它是反应变量和风险参数联合密度函数的对数.目前国内关于分层模型的研究刚刚起步，其中张连增、段白鸽[9](2013)依据损失进展模型LDF模型、Cape Cod模型以及Clark(2003)[10]提出的两种体现损失进展过程的非线性增长曲线——Loglogistic增长曲线和Weibull增长曲线建立了非线性分层模型，后来又将其与贝叶斯理论相融合建立了贝叶斯非线性分层模型(2013)[11]，并做了分层模型在非寿险精算学中应用的研究评述(2013)[12]，指出了HGLM评估准备金的研究前景.除此之外，非寿险领域中尚未见更一般意义下的HGLM理论及应用研究.

HGLM不但可以处理具有相关性的纵向数据、空间聚类数据、甚至更宽泛的聚类数据，为不满足独立性假设且具有层次结构的非寿险赔付数据提供了处理“大规模分类”问题的一种自然方式，而且HGLM能提供统一的贝叶斯信度建模框架，种种优势注定了HGLM技术成为当前国际非寿险精算理论研究的热点领域.随着国内财险公司对GLM在非寿险精算中的应用，相信经过一段时间的实践探索，国内财险公司必然会迫切需要对更合适准备金评估和非寿险定价的HGLM应用研究.鉴于此，建立了分层广义线性模型，利用h-似然函数估计分层广义线性模型的模型参数，降低了计算量.通过推导模型预测误差的估计式来评估模型的预测精度.利用赔付额和赔付次数两种赔付信息建立了未决赔款准备金评估的两阶段分层广义线性模型，并改进了模型的线性预估量使之更加符合真实的赔付规律.提出的未决赔款准备金评估的HGLM，理论上有助于完善未决赔款准备金评估的建模理论和方法，改进模型稳定性、适用范围及预测能力，丰富未决赔款准备金评估领域内的研究内容.在实际应用价值方面，提出的这一改进模型为精算人员提供构建评估模型的新思路与方法，无论对保险公司还是保险监管部门都将提供理论支持和实务参考.

2 分层广义线性模型

设观测变量为Yij，随机效应为U=U(U0,…,Ut)，其中(Ui,Yi0,…,Yit)，0≤i≤t相互独立.在第i个对象的随机效应Ui=ui给定的条件下，Yi0,…,Yit，0≤i≤n相互独立且服从于某一指数分布族：

fYij|Ui=ui(y;θij,φ)

(1)

其中ωij>0是已知权重，θij是典则参数，φ是散布参数.Yij|Ui=ui的条件期望和条件方差如下：

(2)

其中V代表方差函数，其表达式为

V(μ)=b″(b′-1(μ))=b″(θ).

结构假设如下：

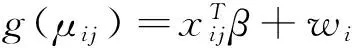
当wi=g(ui)且g(u)=v=b′-1(u)时称g为典则联结函数或自然联结函数.

其中，β为固定效应，对所有观测值都相同.随机分量U 是不可观测的，同一对象的观测值对应的Ui的取值相同，不同对象的观测值对应的Ui的取值不同.u服从任意指数分布族，其离散参数常记为λ.反应变量y|u 和随机效应 u采用不同分布假设，则有与之对应的联结函数.在分层广义线性模型中，如果u的分布为正态分布，则其联结函数w为恒等函数，此时的分层广义线性模型即为广义线性混合模型.y|u 和 u的分布常取为共轭分布，此时分层广义线性模型有一些特殊的性质，易于计算和理解.因此假设风险参数Wi=b′-1(Ui)服从Yij|Ui=ui的指数分布族的共轭分布：

(3)

这里的HGLM其实是一种共轭HGLM，其条件反应变量服从广义线性模型，具有典则联结函数.在线性预估量中有一部分代表已知的协变量，添加项的值由典则函数转化风险参数得到，风险参数服从条件反应变量的共轭分布.常见的共轭HGLM如表1所示.

3 分层广义线性模型的参数估计方法

下面以流量三角形为数据基础给出分层广义线性模型参数估计方法，流量三角形结构如表2所示.

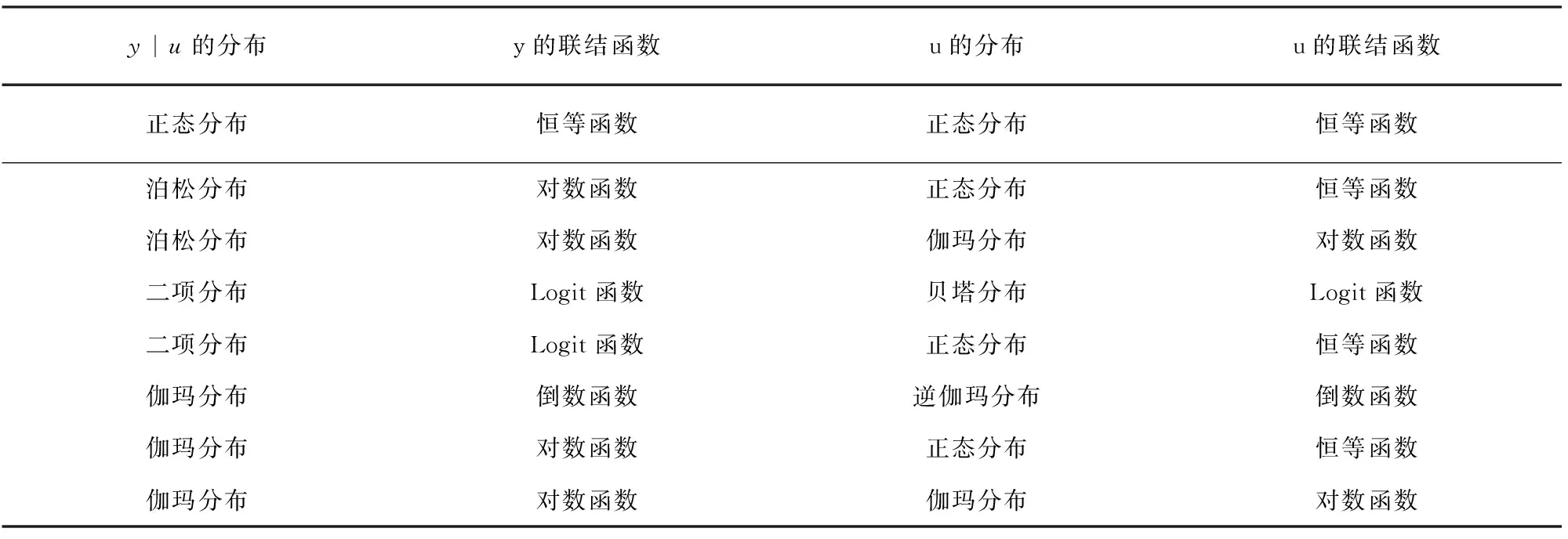
表1 常见的几类共轭HGLM模型

表2 流量三角形

设赔付额或者赔付次数为反应变量Yij，i,j=0,…,t.随机参数Ui，i=0,…,t是事故年i的不可观测的风险参数，描述了事故年i的风险特征.其中，回归参数β称为固定效应，wi，i=0，…，t为随机效应，φ和λ是散布参数.

设xij是Yij的协变量向量，xij包括了任何影响反应变量Yij分布的所有可观测特征的影响.假设影响赔付的所有可观测特征均包含在事故年，进展年和赔付年因素中.不同事故年的反应变量是独立的，但是由于风险参数相同，同一事故年i在不同进展年的响应变量Yij并非独立.这可能是因为在同一事故年重复测得赔付数据的赔付模式相关或者同一事故年的观测值之间存在残差的异质性.

为求解HGLM，Lee和Nelder[6]在1996年介绍了h-似然估计方法，h-似然函数基于流量三角形的观测值y=(yij,i+j≤t)T，是风险参数W=(W0,…,Wt)T和反应变量 Y=(Yij,i+j≤t)T联合密度函数的对数函数，由h≡log fY,W=lY|W=w+lW定义.其中lY|W=w表示Y|W=w的log-似然函数，与Y|U=u的log-似然函数等价，lW是W密度函数的对数.然后，在这个特殊的模型中，将不相关的常数项略去，得到公式(4)：

(4)

其中，由典则联接函数得到：

(5)

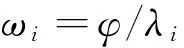
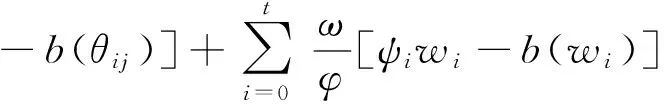
(6)

其中θij参照(5)给出的形式，由于假定ψi，i=0,1,…,t已知，那么似然函数(6)可以视为yij,i+j≤t和ψi扩展GLM的log-似然函数，则相关反应变量和GLM有如下结构：

3)联结函数：g=b′-1(典则联结)

(7)

设计矩阵和回归参数如下：

(8)

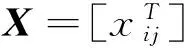
4 分层广义线性模型的准备金预测和预测误差

(9)

(10)

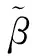
(11)

(12)

条件均值方差作为评估不确定性的一个度量，在给定Dt观测值下由公式(12)定义．

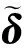
(13)

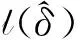
(14)

其中，H11代表似然函数、相应于β和β的衍生矩阵块，H22代表相应于w和w的衍生矩阵块，H12是β和w混合衍生矩阵块.

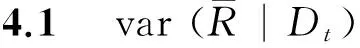
(15)

(16)

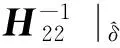
(17)

注意函数r可以被看作是由三个函数的组成，因此雅可比矩阵Jr可以通过J∑JμZ+得到，其中：Z+是函数w的雅可比矩阵；因此Z+是(t(t+1)/2×(t+1))矩阵，其列向量k相应于赔付值Yij的元素在k=i,k=0,…,t时为1.

Jμ是函数(ηij)i=1,…,t(i+j>t)(μij=g-1(ηij))i=1,…,t,(i+j>t)的雅可比矩阵.

J∑是函数(μij)i=1,…,t(i+j>t)∑i,j:i+j>tμij的雅可比矩阵.

(18)

(19)

(20)

据上面公式可得：

(21)

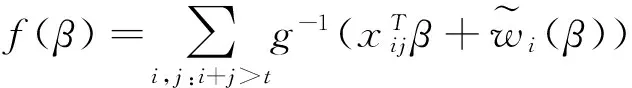
(22)

(23)

(24)

(25)

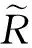
(26)

通过全期望公式，在给定U下Yij条件独立，有：

E(R|Dt)=E[E(R|U,Dt)|Dt]

var (R|Dt)=E[var (R|U)|Dt]

+var [E(R|U)|Dt]

(27)

那么得到：

(28)

之前公式右边第二项的估计值由(26)给出.对于第一项误差，根据模型假定，得到：

(29)

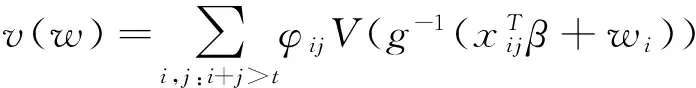
(30)

(31)

(32)

最后，得到：

(33)

其中第一项由(31)给出，第二项由(24)给出.因此，只要参数估计值和费舍信息矩阵估计可用，则这两个等式就可以通过对矩阵微分得到.

5 未决赔款准备金评估的两阶段分层广义线性模型

有了模型的基本结构、参数估计方法以及预测误差，就可以建立未决赔款准备金的评估模型.通常的未决赔款准备金评估模型，往往直接对各单元的累计赔付总额的分布进行假设，并对累计赔付额进行参数估计，忽略了索赔次数和案均赔款等重要数据信息.因此，试图建立一个两阶段分层广义线性模型，该模型分别对索赔次数与案均赔款构造分层广义线性模型，更符合非寿险未决赔款准备金评估的实际需求.此外，改进了模型的线性预估量，使之不但符合随进展年的推延先按幂升再按指数降的赔付规律，而且减少了待估计参数得的个数.

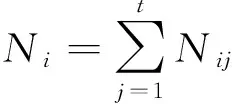
第一阶段模型，对赔付次数建立HGLM.通常假设赔付次数符合二项分布、负二项分布、泊松分布或者过度分散的泊松分布等离散型分布,下面以泊松分布——伽玛分布共轭HGLM为例给出评估模型.

(34)

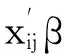
c+αi+ζilnj+γij，

(35)

其形式体现了索赔额除了依赖事故年因素αi外，还随进展年的推延先按幂升再按指数降的赔付规律.Hoerl曲线中的进展年因素类似连续型协变量，对其进行外推可以得到尾部因子的估计.对Hoerl曲线进行简化以减少参数，如式(21)所示.

c+αi+ζlnj+γj．

(36)

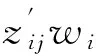
第二阶段模型，对案均赔款额建立HGLM.设案均赔款额服从ED*(指数)类分布，评估模型如式(36)所示.

(37)

6 结 论

在分层广义线性模型的全新视角下建立了未决赔款准备金的评估模型，鉴于流量三角形层次性和相关性的数据结构，在线性预测量中考虑了固定效应和随机效应，并且拓展了风险参数的分布范围.利用h-似然函数估计分层广义线性模型的模型参数，减少了估计过程的计算量.利用参数误差与过程误差的和作为均方误差来评估模型的预测精度，使得模型的精确程度具有可比性.此外，将赔付额和赔付次数两种赔付信息纳入评估模型，建立了两阶段分层广义线性模型，在线性预测量中考虑了各种固定效应和随机效应以及模型结构的散布参数，改进了线性预估量结构，并充分利用了已知赔付信息，这使得分层广义线性模型能够更好的适应各类数据的结构与形式，具有更高的灵活性，在保险实务中可以处理各种赔付规律的案件，较之传统的广义线性模型具有更高的实用性.

[1]KELVINKW,YAUKarenCH,YIPHKYUEN.Modellingrepeatedinsuranceclaimfrequencydatausingthegeneralizedlinearmixedmodel[J].JournalofAppliedStatistics, 2003, 30(8): 857-865.

[2]ANTONIOK,BEIRLANTJ.Issuesinclaimsreservingandcredibility:asemiparametricapproachwithmixedmodels[J]．JournalofRiskandInsurance，2008，75( 3) : 643-676．

[3]KLINKERF.Generalizedlinearmixedmodelsforratemaking:ameansofintroducingcredibilityintoageneralizedlinearmodelsetting[J].CasualtyActuarialSocietyE-Forum, 2011(2):1-25.

[4] 谢远涛,杨娟. 基于操作时间和广义线性混合模型的准备金评估技术研究[J]. 保险研究,2014(3):54-62.

[5] 刘新红,孟生旺. 基于藤Copula的GAMLSS模型与非寿险准备金评估[J]. 经济数学,2014(4):68-74.

[6]LEEY,NELDERJA.Hierarchicalgeneralizedlinearmodels[J]．JournaloftheRoyalStatisticalSociety，SeriesB，1996，58 ( 4 ) :619-678．

[7]GELMANA,HILLJ.Dataanalysisusingregressionandmultilevelhierarchicalmodels[M].Cambridge:CambridgeUniversityPress, 2007．

[8]LEEY,NOHM.Modellingrandomeffectvariancewithdoublehierarchicalgeneralizedlinearmodels[J].StatisticalModelling, 2012, 12(6):487-502.

[9] 段白鸽,张连增. 索赔准备金评估的非线性分层增长曲线模型研究[J]. 财经理论与实践,2013(4):23-29.

[10]CLARKDR.LDFCurve-fittingandstochasticreserving:amaximumlikelihoodapproach[J].CASForum, 2003(3):41-92.

[11]段白鸽,张连增. 索赔准备金评估的贝叶斯非线性分层模型[J]. 山西财经大学学报,2013(10):20-31.

[12]段白鸽,张连增. 分层模型在非寿险精算学中的应用研究评述[J]. 统计研究,2013(05):98-105.

[13]BOOTHJG,HOBERTJP.Standarderrorsofpredictioningeneralizedlinearmixedmodels[J].JournaloftheAmericanStatisticalAssociation, 2012, 93(441):262-272.

[14]LEEY,HAID.OrthodoxBLUPversush-likelihoodmethodsforinferencesaboutrandomeffectsinTweediemixedmodels.StatisticsandComputing2010, 20(3): 295-303.

Modeling Study of Hierarchical Generalized Linear Model in the Assessment of the Reserve

YAN Chun, LI Yan-xing, CHEN Xiang-hui, QIU Yi-wei

(College of Mathematics and Systems Science , Shandong University of Science and Technology， Qingdao, Shandong 266590,China)

By considering the longitudinal characteristics of repeated measurements over time of loss for a given accident year in the loss runoff triangles and regarding the loss runoff triangles as hierarchical data, this paper established a hierarchical generalized linear model. Compared with the usual stochastic model, the hierarchical generalized linear model can choose the distribution of conditional response variables and the distribution of risk parameters is more extensive. Using the h-likelihood function to estimate the model parameters of the hierarchical generalized linear model, the calculation amount was reduced. In order to make the model to be comparable, the prediction accuracy of the model was evaluated, and the estimation formula of the model prediction error was derived. In order to make full use of the known payment information, a two-stage hierarchical generalized linear model was established to consider two payment information -the number of compensation and the amount of compensation. The linear prediction considers the distribution parameters of fixed effects, random effects and the distribution parameters of the model structure. The research shows that the hierarchical generalized linear model has good adaptability to all kinds of distribution and form of the data, and it is more consistent with the real payment rule in the insurance practice.

insurance mathematics; hierarchical generalized linear model; h-likelihood function; prediction error

2016-01-12

国家自然科学基金项目(61502280)；青岛市应用基础研究计划项目(青年专项)(14-2-4-55-jch)；山东省自然科学基金面上项目(ZR2014FM009)；山东科技大学研究生教育创新计划项目(KDYC14016)

闫 春(1978—)，女，山东邹城人，副教授，工学博士E-mail:yanchunchun9896@sina.com

F840.65

A