液位传感器容错控制方法研究

何 宁，那文波，何伟迪，徐 川，武雅仙

(中国计量大学 机电工程学院，杭州 310018)

液位传感器容错控制方法研究

何 宁，那文波，何伟迪，徐 川，武雅仙

(中国计量大学 机电工程学院，杭州 310018)

PID(比例-积分-微分)控制法在液位过程控制中发挥着重要作用，但由于液位系统传感器容易发生故障，使得PID控制法具有抗故障能力不足的缺陷，对生产生活造成重大损失，因此需采用容错控制方法使得液位传感器发生故障时仍能较为正常运行，提出状态观测器估计传感器液位故障值的容错控制方法，使状态观测器对故障状态产生观测跟踪，将故障状态作用于原控制器，并使原控制器弃置已经存在故障的传感器信号，使得故障值被抵消。

液位传感器；状态观测器；容错控制

0 引言

传统的液位控制系统多采用PID(比例-积分-微分)控制法。这种传统的液位控制系统具有结构简单、易于实现等优点，因此至今仍然在液位过程控制中占据主要地位，但是其缺点也不容忽视，主要缺点是抗故障的容错能力低下[1]。有时在故障发生时，即使能迅速判断故障的存在、故障的位置甚至定量分析故障，但系统故障产生的损失也已不可避免，因此需要引入容错控制系统尽量保证液位控制系统在发生故障时仍可以稳定运行并具有可以接受的性能指标。

液位控制系统传感器最易发生故障，系统多采用压力传感器测量液位。压力传感器由相应的测量电路组成，测量电路的某些电子元件的故障是传感器产生故障的源头。本文基于电容原理的液位传感器，通过测量电路的输入-输出表达式确定联立方程组求解的故障诊断方法，在此基础上提出了基于线性变参数观测器估计系统状态并实现控制的容错控制方法。

1 液位控制系统状态空间描述的建立

1.1 单容液位控制系统状态空间描述的建立

如图1的单容液位控制系统，若水箱横截面积为S，液位为h，水箱流入量为Q1，流出量为Q2，有：

(1)

对于流出量为Q2，由于通过阀门的流体是紊流，有：

(2)

对于流入量Q1，通过入流控制泵调节，有：

Q1=KpVp(t)

(3)

其中：Vp(t)为加在控制泵上的电压，Kp为泵常量(m3/V·s)。得到：

(4)

以Vp(t)为状态输入量u(t)，液位h(t)为状态向量x(t)、状态输出量y(t)。对于线性系统，其状态空间表达式的标准描述为：

(5)

x2h2(t)+x1h(t)+x0

(6)

同时矩阵A将变成线性变参数形式，得到单容液位控制系统的线性变参数状态空间表达式：

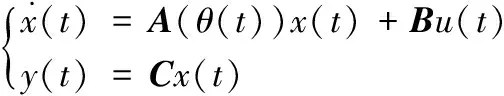
(7)

其中：

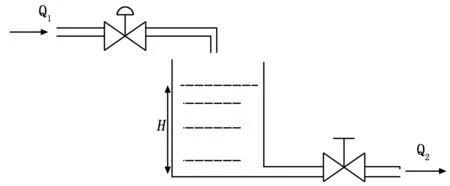
图1 单容液位控制系统原理图

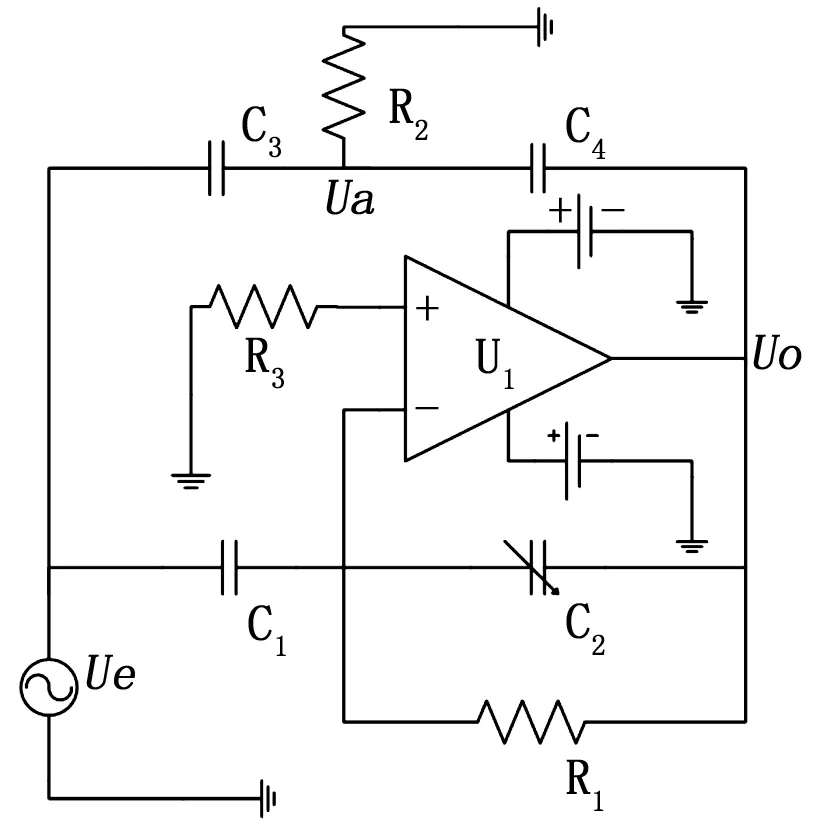
图2 实际传感器测量电路

1.2 双容液位控制系统状态空间描述的建立

对于双容液位控制系统如图3，通过阀门1将储水器的水运送到水箱1中，加在入流控制泵上的电压Vp(t)作为状态输入量。水箱1的出水阀门即水箱2的入水阀门，水箱1能起到控制水箱2液位的作用，在设计反馈控制系统整定PID参数后能实现水箱1液位的恒定和水箱2液位对水箱1的跟随。假定两个水箱的横截面积、阀门横截面积都相同。

图3 双容液位控制系统原理图

双容液位控制系统的水箱1状态表达式与单容类似，对于水箱2，有：

(8)

根据公式(7)可推出双容液位控制系统的线性变参数状态空间表达式：

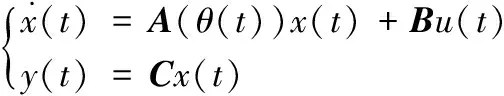
(9)

其中：

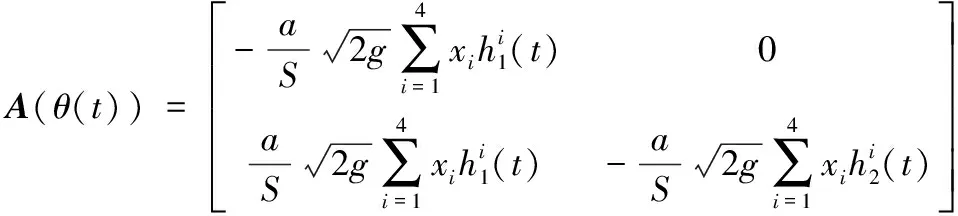
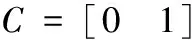
对于液位控制系统，关于公式(6)中的xi取值，参考[2]，取x4=2.981×10-7，x3=-3.659×10-5，x2=1.730×10-3，x1=-4.036×10-2，x0=0.583。

2 容错控制的原理

对于可用状态空间表达式描述的线性系统，可采用状态反馈配置极点使系统具有抗干扰性、鲁棒性。有时系统某些状态不能直接物理测量(如液位传感器出现故障，无法实时得知液位)，这时采用状态观测器基于输出和控制变量估计状态。在容错控制中，使用状态观测器估计出实时故障状态，原控制器根据估计状态进行控制，而不再使用传感器所测状态，即为容错控制的基本原理。

状态观测器可观测到系统所有状态变量时称为全维状态观测器。在只需要观测不可物理测量的状态变量时，只实现观测部分状态变量的观测器称为降维状态观测器[3]。无论何种观测器，均必须保证系统具有可观性。

设计观测器时，对于公式(9)形式的线性变参数系统，若系统可观，构造一个模拟系统的动态方程，形式与公式(9)相同。

(10)

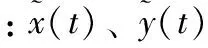
(11)

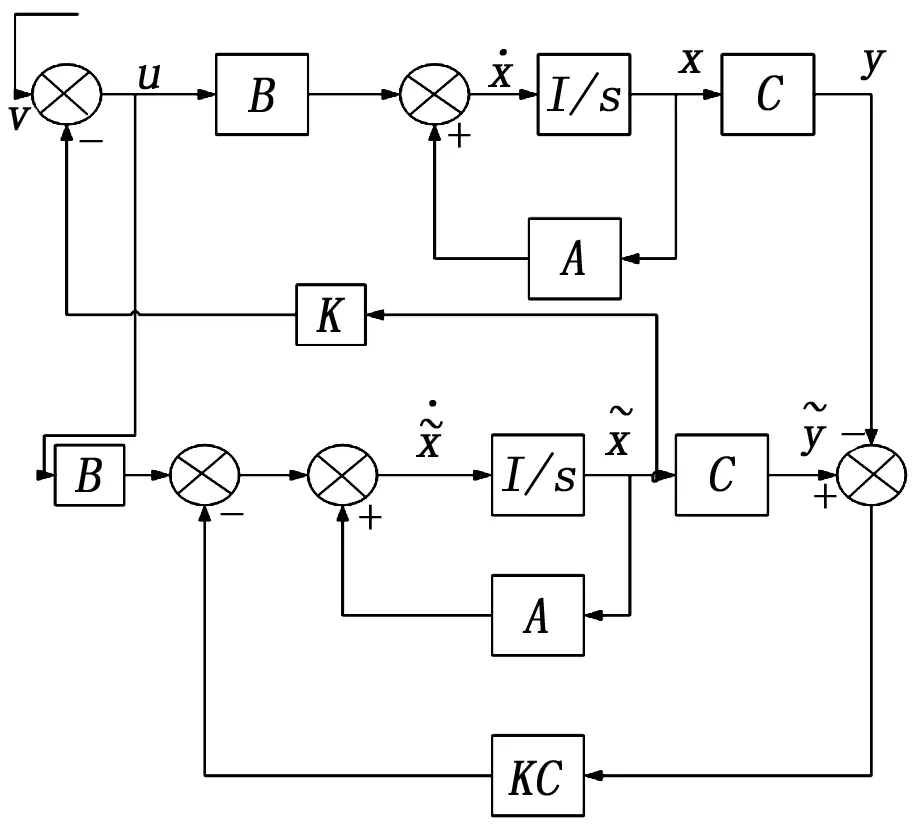
图4 状态观测器控制图

式(5)减去(11)，得：

(12)

(13)

3 基于系统观测器的液位传感器容错控制设计

3.1 线性变参数状态观测器的表达式

上一节中，液位控制系统的状态空间已经建立，为线性变参数系统。因此需要设计线性变参数系统的状态观测器。现以双容液位控制系统状态为例，在公式(9)基础上，建立包括故障函数f(t)的线性变参数系统状态空间描述方程:

(14)

其中:

将两个水箱的液位都作为输出量，因此系统为双输出。此时C=I2。

(15)

注意到向量θ(t)在拥有22=4个顶点的超方形内变化(上界定为θmax，下界定为θmin)。定义超方形4个顶点为Λj(j=1,2,3,4)，且有:

Λj∈{(ϑ1,j,ϑ2,j)|ϑ1,j,ϑ2,j∈{θmin,θmax}}

(16)

ϑ1,j和ϑ2,j分别为Λj的两个元素，此推导式有助于下文线性变参数观测器矩阵的求取。

为保证状态观测器可以设计，公式(16)必须满足如下条件：

1)A(θ)中液位拟合系数xi有唯一确定值，此要求应用文献[5]的数据已符合；

2)rank(C)=rank(A)。对于公式(16)所描述的双容液位系统状态方程，A和C的秩都是2，因此此条件也得到满足。

3.2 液位传感器容错控制系统的基本框架

根据上述推导，得到了基于线性变参数观测器的具有故障诊断功能和容错性能的液位控制系统，该系统在液位传感器测量电路出现故障导致测得液位与实际液位不符时，一方面采用故障诊断方法实现故障定位和故障定值；另一方面，线性变参数观测器对状态向量(即液位高度)进行观测跟踪，得出其估测值，此时标称PID控制器采用状态估测值进行控制，使液位控制系统正常运行。液位传感器容错控制系统如图5所示。

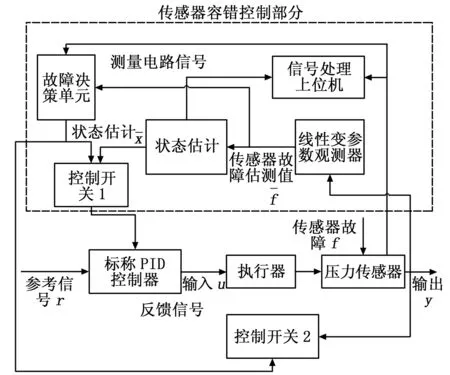
图5 液位容错控制系统框架图

总结出液位控制系统液位传感器容错控制系统的设计步骤算法[6]。

步骤2：求取矩阵不等式(17)的解，得到矩阵P、Pz、Z的值，以及正标量γ的允许最小值；

(17)

步骤3：确定线性变参数观测器的表达式，将矩阵Z的值和步骤1求得的Γ1、Γ2、WT、WTC、G代入公式(21)，得到N(θ)、L(θ)、T、Q矩阵的表达式；

(18)

(19)

(20)

(21)

4 仿真验证

根据3建立起来的基于线性变参数观测器的液位传感器容错控制系统，代入实际的参数值进行计算并仿真[7]。

对于图3所示双容液位控制系统，两个水箱均有液位传感器测量液位，且两个液位传感器都可能故障但假定水箱2的传感器有替代品，因此系统状态维数n、输出维数p均为2，而传感器故障维数r为1。

设定两水箱横截面积S、阀门横截面积a都相等。根据公式(9)的双容液位控制系统的线性变参数状态空间表达式，对于输出量y(t)，考虑到噪声信号no(t)，有:

(22)

其中:h1(t)、h2(t)分别是水箱1、水箱2的液位高度，Kp为泵常量(m3/V·s)，u(t)是图3加在入流控制泵上的电压，n1(t)、n2(t)分别为液位传感器的测量噪声。令:

S=15.5 cm2a=0.178 1 cm2

Kp=3.3 cm3/V·sg≈980 cm/s2

(23)

对于传感器正常状态下的标称控制，取:

u(t)=-13.474 9 h1(t)-45.262 4 h2(t)-

(24)

此标称控制法在没有传感器故障时根据参考信号r(t)调整水箱2的液位。此处液位高度量纲取cm，输出噪声n1(t)、n2(t)多数情况下小于0.3 cm。现将噪声信号设定为高斯白噪声，所乘系数为0.3。

水箱1传感器无即时替代，故f(t)=f1(t)，其以液位为量纲的故障表达式随时间而变化，有:

(25)

当t<15 s时，水箱1液位传感器的正常工作；当15 s≤t<100 s时，传感器发生测得液位有周期性变化的的故障；当t≥100 s时，传感器发生彻底性故障，导致传感器输出信号为0。参考信号r(t)为要求水箱达到的液位，假定最初设定为18 cm，t≥50 s后设定为27 cm，t≥100 s后设定为22 cm。线性变参数观测器对系统状态、传感器故障值进行估计，使得此时液位上升时间增加，仍以被控水箱2液位达到稳态值95%-105%为标准，当t=15 s故障发生时，水箱2液位恰好处于稳态，线性变参数观测器只用了约0.6 s就能使被控标称控制器将液位恢复至稳态，当参考信号由18 cm上升至27 cm时，h2(t)滞后时间有10.3 s，当参考信号由27 cm下降至22 cm时，滞后时间7.8 s。在传感器故障下，当参考信号r(t)变化时，水箱液位相对于参考信号的滞后速率低于1.5 s/cm[8]。

5 总结

本章研究了双容液位控制系统传感器故障的容错控制方法。首先根据液位控制的基本原理得到系统状态空间表达式，其中采用了非线性参数拟合使得状态系数矩阵为关于状态的参数多项式形式；接下来引入线性变参数观测器实现容错控制，最后代入实际液位控制系统具体参数，得到线性变参数观测器的具体表达式。以二维状态、二维输出信号但传感器故障维数一维的双容液位系统故障为例，采用MATLAB进行仿真，验证了观测器对传感器故障值估测的精确性和系统对传感器故障的容错性[9]。

[1] 吴祚武.液位控制系统[M]. 北京: 化学工业出版社,2006.

[2] Forsythe G E, Malcolm M A, Moler C B. Computer methods for mathematical computations[M]. Prentice Hall,NJ,USA, 1977.

[3] 王永骥, 王金城, 王 敏. 自动控制原理[M]. 北京: 化学工业出版社,2007.

[4] Ali A, Mohamed Z. Sensor-fault-tolerant control for a class of linear parameter varying systems with practical examples[J]. IEEE Transactions on Industrial Electronics, 2013,60(11):5239-5251.

[5] 张玉燕,孙敬武,罗小元,等.双容液位系统鲁棒自适应容错控制[J].控制工程,2010,17(3):324-327.

[6] 周东华, Ding X. 容错控制理论及其应用[J]. 自动化学报, 2000, 26(6): 788-795.

[7] Zhou D H,Zhou J L,et al.Fault detection and diagnosis of singular stochastic distribution systems[A]. 7th World Congress, Intelligent Control and Automation[C].2008, 274-279.

[8] Asan M K, Valarmathi K. Fuzzy modified model Reference adaptive controller for Improved Transient Response[A]. 2013 International Conference on Power, Energy and Control[C]. 2013: 454-457.

[9] 叶银忠, 潘日芳, 蒋慰孙. 控制系统的容错技术的回顾与展望[A]. 第二届过程控制科学论文报告论文集[C].1988: 49-61.

Liquid Level Sensor Fault-tolerant Control System Research

He Ning，Na Wenbo，He Weidi，Xuchuan，Wu Yaxian

(College of Mechanical and Electrical Engineering，Chinese Jiliang University，Hangzhou 310018,China)

Traditional PID (proportional integral differential) control occupied the main position in the process of liquid level control, but because of the liquid level control system, especially the malfunction of the sensor is easy to make PID control method has the defects of lack of ability to resist failure, caused heavy losses in the production, so the need of fault diagnosis for liquid level control system running state and judge for abnormal situation, and provide the basis for system maintenance, according to the results of the diagnosis of the fault-tolerant control system makes the liquid level sensor failure could be run normally, still put forward state observer to estimate liquid level sensor fault values of fault-tolerant control system, the state observer for fault status tracking, and the fault state role in the original controller and make the original controller dumping existing fault of sensor signal, the fault value is offset.

liquid level sensor; fault diagnosis; state observer; fault-tolerant control

2016-06-06；

2016-08-10。

何 宁(1988-)，女，河南开封市人，硕士研究生，主要从事故障诊断与容错控制方法研究。

那文波(1963-)，男，辽宁抚顺人，硕士，教授，硕士生导师，主要从事故障诊断、控制算法等方向的研究。

1671-4598(2016)12-0241-04

10.16526/j.cnki.11-4762/tp.2016.12.070

TP302.6

A