基于Dubins曲线和改进A*算法的AUV路径规划方法

胡 蔷1，高立娥1，2，刘卫东1，2，李泽宇1

（1.西北工业大学航海学院，西安 710072；2.水下信息与控制国家重点实验室，西安 710072）

基于Dubins曲线和改进A*算法的AUV路径规划方法

胡 蔷1，高立娥1，2，刘卫东1，2，李泽宇1

（1.西北工业大学航海学院，西安 710072；2.水下信息与控制国家重点实验室，西安 710072）

将Dubins曲线和具有角度约束的改进A*搜索算法结合应用于路径规划中，能解决路径长度最短和安全性的问题。这样规划出来的路径由两段满足AUV最小转弯半径的圆弧和一段同时与两弧相切的直线构成；圆弧段由产生Dubins路径的方法产生，直线段由改进A*搜索算法扩展产生；首先通过判断Dubins路径存在条件，解算Dubins曲线参数，从而确定此路径中两圆弧的起始点、终止点坐标；再通过这些圆弧坐标可得到直线与圆弧的切入点、切出点，此两点就是改进A*搜索算法扩展路径的起始点和终止点；以Matlab为工具进行仿真实验，验证了此方法能产生规避障碍物的可行的最短路径。

Dubins曲线；改进A*搜索算法；路径规划；Matlab

0 引言

自主式水下航行器（autonomous underwater vehicle，AUV），具有活动范围大、机动性好、安全并且隐蔽性好等优点，从60年代中期起，工业界和军方开始对其发生巨大兴趣。AUV是利用自身传感器，搜集环境中的信息，采用一定的算法建立周围环境的模型，控制其在环境中按照预定的路径航行到目标位置［1-3］。AUV研究领域的范围很广，但是路径规划是最基础也是最必要的部分，在复杂的海洋环境中，它保证AUV的有效行驶并完成给定的任务要求。

AUV路径规划方法多种多样，目前大都是从地面机器人系统借鉴来的，后来人们将室内地面机器人技术加以提升和改进，应用到空中和水下［4 5］。Voronoi图法，就是Chandler等最先采用的，在已知环境内，产生的单架无人机路径的方法［6］。概率法中，Eagle和Yee将路径规划看做是分割单元内的搜索问题［7］。对于单元分解法，Kambhampari和Davis提出了一种减小内存使用率的估计法，成为四叉树或八叉树表示法［8］。但这些使用了全局搜索和计算方法的Voronoi图法、随机概率图法和单元分解法都没有考虑路径的运动学约束，而AUV航行每一时刻存在速度和方向，所以这些路径规划方法都是有缺陷的。

1975年，Dubins在研究中指出，平面内满足最小转弯半径约束的两个矢量间的最短路径是由直线和圆弧段组成的复合路径。Balkcom和Mason使用Pontryagin最大化原理证实一般的移动机器人在平面内的运动是直线与弧线的组合［9］。所以本文设计一种将Dubins路径和改进的A*算法结合的路径规划方法，产生一种圆弧和直线相结合的路径，在路径始末两端引入了圆弧，有效解决了AUV航行机动性和终端约束的问题，圆弧之外的路径用改进的A*算法扩展产生。在无障碍物的情况下，路径总长度是满足最小转弯半径的两个圆弧和它们之间的切线之和，是长度最短的路径。在有障碍物的情况下，圆弧部分通过扩大圆弧半径方法规避障碍，直线部分用改进A*算法的节点评价函数自主产生规避障碍的路径，这样产生的的路径仍然是满足安全性约束的最短路径。

1 Dubins曲线

由于AUV每时每刻都有速度和方向，有必要在带有方向的初始位置（起始位姿点）和终止位置（终止位姿点）间寻找最短路径。

两个位姿点间的最短路径就是Dubins路径。Dubins路径可以简单地被定义为，在最大曲率限制下，平面内两个有方向的点间的最短可行路径是CLC路径或CCC路径，或是他们的子集，其中C表示圆弧段，L表示与C相切的直线段。

1.1 Dubins存在的条件

设计Dubins路径时，需要寻找直线段与两圆弧的切点，如果找不到切点，那么Dubins路径就不存在。

用公式表示Dubins存在的条件［2］，式（1）表示存在外切

式中，rt表示终止圆弧半径，rs表示起始圆弧半径，c表示两圆弧圆心连线的长度。

1.2 参数计算

对于已知起始位姿点、终止位姿点的路径规划问题，一旦经过式（1）和（2）验证存在Dubins路径，那么就存在本文所设计改进A*算法和Dubins曲线结合的路径，求解此路径只需求解Dubins路径参数。

以二维平面为例，已知某AUV速度25 m／s，路径起始点S坐标为（0，0），单位m，起始航向角α为90°，终止点T坐标（700，700），单位m，终止航向角β为135°，最小转弯半径rmin为100 m，对于起始圆弧、终止圆弧都是最小转弯圆的Dubins路径，可以判断出同时存在具有内切线和外切线的两种Dubins路径，显然AUV只能向前运动，且根据起始点终止点角度约束，只有如图1所示路径SPsPtT满足要求。

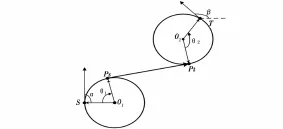
图1 两圆弧半径均为100 m时的Dubins路径曲线

用微分向量方法求解路径参数方法解此路径的参数［10-13］。起始点为S，目标点为T，位置变换向量P有如下可得：

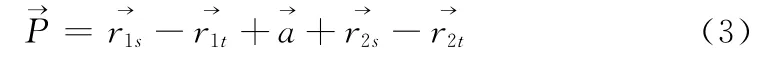
解θ2即可。再用解析几何的方法可以求解两圆弧圆心O1、O2，和直线切圆弧的切入切出点Ps、Pt。θ1、θ2即为A*算法和Dubins曲线结合产生的路径的起始圆弧圆心角和终止圆弧圆心角。Ps、Pt即为上述路径直线部分的起始点与终止点。已知这些路径参数就可以得到完整的路径曲线图。

2 A*搜索算法

传统A*算法将规划空间划分为网格的形式，通过起始节点所在网格，通过节点评价函数，选择相邻节点所在网格不断向目标节点所在网格进行扩展。算法具有搜索速度快，搜索结果优的特点。但基于网格的节点扩展方式，将网格中心点连接而成的路径，难以适合具有一定运动方向和运动性能限制的运动，路径必须进行平滑修正。

2.1 改进的A*算法

对传统A*算法进行缺陷分析，明确了传统A*算法没有考虑到路径平滑性要求，因而通过在传统A*算法中加入角度信息，而引入一种改进的A*搜索算法。

AUV在水下运动时由于受过载和最小转弯半径的限制，在Δt时间内可转的角度Δψ一定（Δψ＜Maxψ，Maxψ为AUV在一定速度、时间范围内可转过的最大角度），所以在搜索待扩展节点时，搜索范围是以当前速度矢量为中心的扇形区域内，扇形半径即为搜索步长。

以二维平面为例，用改进的A*搜索算法扩展节点如图2所示。建立水中某一深度下的平面坐标系OXY，设鱼雷起始点S（xs，ys），速度方向为OS所指方向，初始航向角为ψ0＝∠SOX，搜索步长为L，待扩展节点P1i（P1i＝［p11，p12，p13.....］，SP1i＝L）可能存在的范围是以2maxψ为圆心角，以OS为角平分线的扇形区域的圆弧上，扇形的半径为L。

2.2 障碍规避

对于如图2所示的路径节点扩展方式，在没有障碍物的情况下，Dubins路径的非圆弧段能扩展成一段切于两圆弧的直线，但是在障碍物环境中接下就不一定是直线。在具有障碍物的环境中从起始点S准确扩展路径节点直到目标点T，就要依据节点评价函数。

扩展节点的评价函数如下定义：

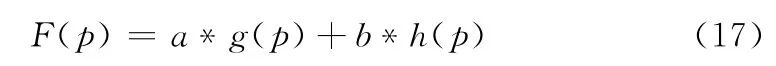
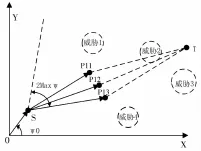
图2 改进的A*算法扩展节点图

式中，g（p）表示初始路径节点S到当前节点P的最小路径代价的估计值，h（p）表示从当前节点P到目标节点T的最小路径代价的估计值，a和b表示真实代价和预计代价的加权，F（p）表示从初始节点S经节点P到目标节点T的最小路径代价的估计。

定义g（p）为：

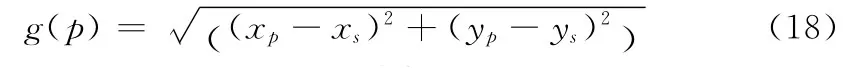
表示当前节点与初始节点间距离。

定义h（p）为：

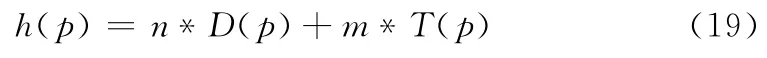
式中，D（p）表示当前节点P到目标节点T的路径代价，T（p）表示当前节点P到目标节点T的威胁代价，n和m分别表示路径代价和威胁代价的权值。n，m不同的权值组合反映了AUV更侧重于选择较短的路径来减少损耗或是更侧重于远离威胁使路径更安全。

定义P点的路径代价D（p）为：

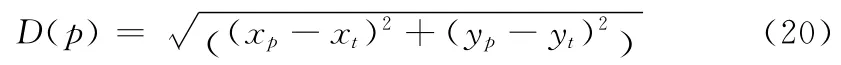
表示当前点P到目标点T的距离。

威胁代价T（p）的估计函数具有多种形式，不同形式的估计函数对节点的威胁评估不一定相同，而且在不同估计函数下，路径规划耗时也不一定相同。给出了一用常用的威胁代价评估函数［14－16］如式（21）所示：

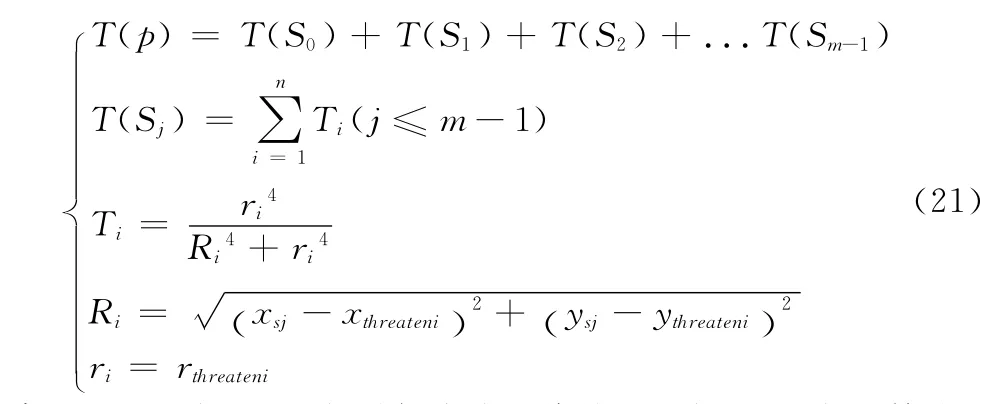
式中，T（Sj）表示Sj点到各威胁的代价，Ri表示Sj点到第个i威胁的距离，ri表示第i个威胁的威胁半径，（xsj，ysj）表示Sj点的位置坐标，（xthreteni，ythretani）表示第i个威胁在空间中的位置坐标。

威胁代价T（p）不仅对当前节点威胁代价做出评估，还对选取该节点后可能采用路径所面临的威胁代价做出评估，有利于算法向更可行的区域经行扩展与搜索。

3 仿真实验

根据2.2例子中给定的AUV基本信息，对本文所设计的路径规划方法进行仿真验证。图3是无障碍物情况下，假设起始转弯半径与终止转弯半径相等，AUV转弯半径逐渐增加的路径仿真曲线，它们的半径依次为100 m，150 m，200 m， 276.5 m。曲线的存在满足了AUV航行路径平滑性要求，直线由改进A*算法扩展而来，由于无障碍物，非圆弧段扩展成直线，曲线与直线相切，满足路径连续性要求。半径为100 m时，路径最短，路径损耗最小。

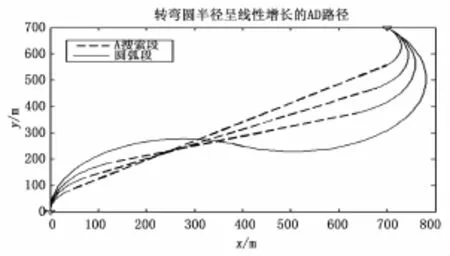
图3 圆弧半径递增的路径曲线

当存在障碍物，并且存在于非圆弧段时，原来的直线部分根据节点评价函数重新扩展可行的安全路径，此时就不是扩展成直线了。改进A*搜索算法规避障碍物通过在式（19）中选取不同的n，m组合来确定选择较短的路径还是远离威胁来规划路径。这里，n＝0.168，m＝5.05表明此时规划路径侧重于规避障碍。此时路径长度虽大于无障碍时扩展的直线长度，但却是满足安全性约束的最短路径。路径参数见表1。规划的路径曲线如图4所示。

表1 路径参数表半径

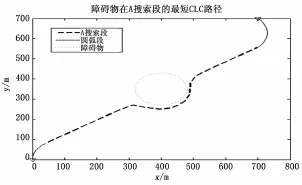
图4 非圆弧段路径存在障碍物的路径曲线

当障碍与存在于圆弧段并且存在于目标点所在的圆弧段时，根据2.2节计算出路径参数见表2。通过调整终止圆弧的半径长度可以达到规避障碍的目的。规划的路径如图5所示。

表2 路径参数表半径

4 结束语

路径规划的最基本也是最重要的两个约束就是路径的可行性及安全性，即路径需要满足切线连续性和规避障碍物性能。通过以上的算法分析，实验仿真，验证了本文所设计的路径规划算法的有效性和高效性，即通过引入Dubins路径的圆弧段解决了大多数路径规划算法不满足运动学约束的缺陷，通过在直线段运用最好优先搜索的改进A*搜索算法，使AUV在此部分自主规避障碍物，且用此方法规避完障碍物的路径长度也是满足约束条件下最短最优的路径。

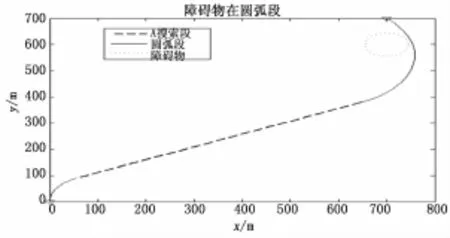
图5 目标点所在圆弧段存在障碍物的路径曲线

［1］徐德民.鱼雷的自动控制系统［M］.西安：西北工业大学出版社，2001.

［2］严卫生.鱼雷航行力学［M］.西安：西北工业大学出版社，2005.

［3］高 剑，刘富樯，严卫生.自主水下航行器回坞路径规划与跟踪控制［J］.机械科学与技术，2012，31（5）：810-813.

［4］沈林成，多无人机自主协同控制理论与方法［M］.北京：国防工业出版社，2013.

［5］Tsourdos A，White B，Shanmugavel M.Cooperative path planning of unmanned aerial vehicles［M］.祝小平，等译.北京：国防工业出版社，2103.

［6］Chadler P，Rasmussen S，Pachter M.UAV cooperative path planning［J］.AIAAGuidance，Navigation，andControl Sciences，2000，：167-194.

［7］Eagle J，Yee J.An optimal branch－and－bound procedure for the constrained path，moving target search problem［J］.Operations Research，1990，28：110-114.

［8］Kambhampari，L S，Davie L S.Multi-resolution path planning for mobile robots［J］.IEEE Journal of Robotics andAutomation，1986，2（3）：135-145.

［9］Balkcom D J，Mason M T.2000.Extremal trajectories for bounded velocity differential drive robots［A］.Proc.IEEE Int.Conf.onRobotics andAutomation［C］.SanFrancosco，pp.2479 -2484.

［10］梁 勇，张友安，雷军委.一种基于Dubins路径的在线快速航路规划方法［J］.系统仿真学报，2013，25：291-296.

［11］张友根，张友安.基于双圆弧原理的多导弹协同制导律研究［J］.海军航空工程学报，2009，24（5）：537-541.

［12］张友根，张友安，邬寅生.基于Dubins路径的多飞行器协同在线航路规划的研究［A］.第六届博士学术年会［C］.重庆：中国科学技术出版社，2008.

［13］吴友谦，裴海龙.基于Dubins曲线的直升机曲线规划［J］.计算机工程与技术，2011，34（4）：1426-1429.

［14］周 良，王耀南，印 峰，等.基于类三维地图的无人机路径规划［J］.计算机测量与控制，2011，19（11）：2788 2790，2794.

［15］郑昌文.飞行器航迹规划方法研究［D］.武汉：华中科技大学，2003.

AUV Path Planning Method Based on Improved A* Search and Dubins Curve

Hu Qiang1，Gao Lie1，2，LiuWeidong1，2，Li Zeyu1

（1.School of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China；2.State Key Laboratory of Underwater Information and Control，Xi′an 710072，China）

The application of the Dubins curve and the improved A*searching algorithm with angle constraint in the path planning，can solve the problem of the shortest path and route security.The path generated by this method，is composed of two circular arcs and a straight line which tangents to them.The circular arc which has the minimum turning radius，was produced by the Dubins curves，while the straight line by the A* searching algorithm.First，by judging the existing condition to calculate the parameters of Dubins’curve，then the coordinates of the starting point and terminal point can be calculated.With the coordinates，we can calculate the entry point and cut－in point of the straight line and arcs.And these two points will be the starting and terminal points which improve the A*searching algorithms’propagating path.The Matlab simulation experiment verified that the path produced in this way is the shortest one to avoid the obstacles.

Dubins curve；improved A*searching algorithm；path planning；Matlab

1671-4598（2016）08-0259-04

10.16526／j.cnki.11－4762／tp.2016.08.071

：TP391.9

：A

2016-02-29；

：2016-03-26。

国家自然基金项目（61473224）；水下信息与控制重点实验室基金项目（9140C230202150C23001）。

胡 蔷（1989-），女，陕西西安人，硕士研究生，主要从事计算机控制与系统仿真方向的研究。