基于单次反射圆模型的混合定位算法研究

陆 音，项 政

（南京邮电大学江苏省无线通信重点实验室，南京 210003）

基于单次反射圆模型的混合定位算法研究

陆 音，项 政

（南京邮电大学江苏省无线通信重点实验室，南京 210003）

针对现有定位算法抗非视距能力弱、且对移动台求解时往往需要一个比较精确初始解的问题，利用移动台和散射体的几何位置关系，基于单次反射圆模型提出了一种抑制非视距误差的波达时间／波达角混合定位算法；定位过程中将散射体视为虚拟基站，根据最大散射半径确定移动台的可能位置范围，在该范围内搜寻所有满足约束条件的位置点，对这些点使用加权平均处理方式以提高定位精度，最后结果即为移动台估计位置；计算机仿真表明了算法的有效性。

单次反射圆模型；波达时间／波达角；非视距；虚拟基站；混合定位

0 引言

当今社会移动通信技术迅猛发展，智能手机快速普及，基于位置的服务产业在国内外已经成为继互联网产业之后的一个新的市场爆发点。在此背景下，无线定位技术受到了各大公司和研究机构的广泛重视。无线定位研究领域中，除了常用的GPS定位技术，移动台定位也是目前国内外的研究热点。但在实际定位时，由于信号在传播过程中通常会受到散射体和障碍物的影响，从而导致传播信号发生折射、反射、衍射等现象，会对定位精度产生严重影响，即NLOS误差。

为了抑制NLOS误差，提高定位精度，目前研究热点大多集中在TDOA／AOA、TOA／AOA［1 3］等混合定位算法上。混合定位算法从求解原理上可以分为线性定位算法和非线性定位算法。线性定位算法源于视距定位算法，通过将移动台的可能位置范围由一块区域压缩至一条直线，然后根据这些定位直线的交点确定移动台估计位置。该算法具有较低的计算复杂度，缺点在于定位精度比较差。为了提高定位精度，通常使用的是非线性定位算法。非线性定位算法将定位问题转化成约束优化问题后求解，以完成对MS的定位估计，缺点在于需要一个较为精确的初始估计才能获得比较良好的定位精度，初始估计的获取通常是这些算法的难点所在。

针对上述问题，本文在单次反射圆模型［4-5］的基础上，利用MS和散射体的位置关系确定MS的可能位置范围，直接搜索出移动台的所有可能位置点，解决了初始点的估计问题；同时为了提高定位精度，利用加权平均的方式对这些可能位置点进行处理，最终获得MS的估计位置。仿真表明该算法在NLOS环境下可以在一定程度上减弱NLOS误差带来的影响。

1 算法描述

1.1 定位过程

定位过程如图1所示，在单次反射圆模型中，信号在传播过程中都经历了唯一的一次反射，且散射体均匀分布在以MS为中心、半径为Rd的散射圆内。信号传播距离等于MS到散射体的距离与散射体到BS的距离和，即：

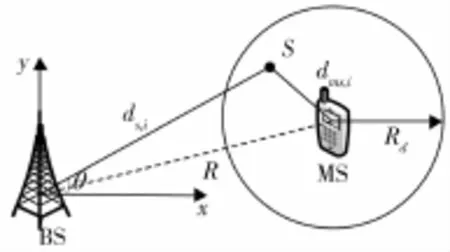
图1 单次反射圆模型

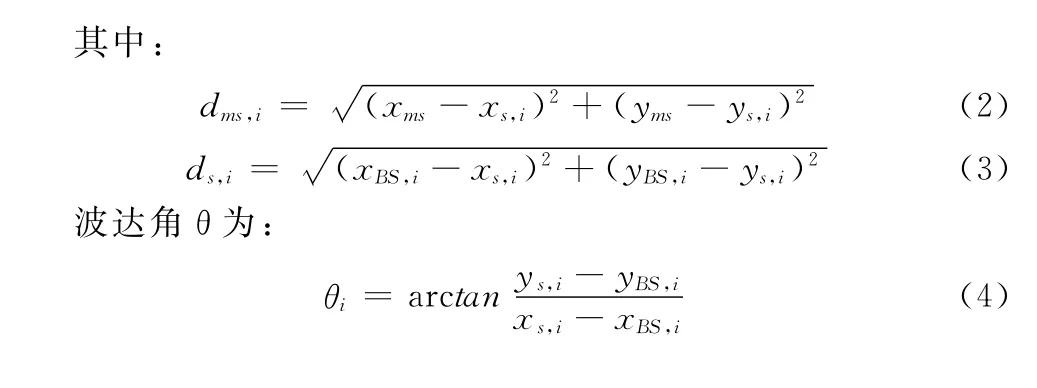
由于测量误差的存在，式（1）和式（4）往往并不成立，所以在对MS进行定位时，可以通过最小化如下的目标函数进行求解：

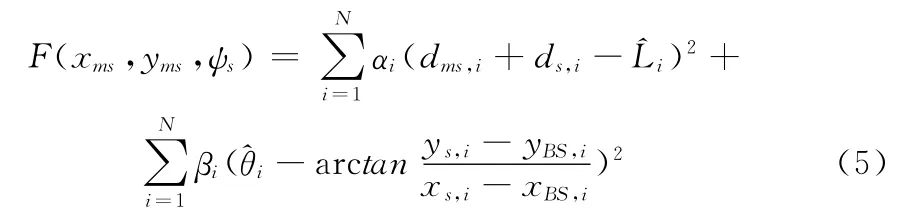
其中：ψs表示散射体的坐标，αi、βi为反映第i个测量值可靠性的权值。因为无法获取散射体Si的坐标，所以传统TOA／AOA混合定位算法（如文献［2］中的HTA算法）是通过最小化式（6）的目标函数来实现对移动台的位置估计：

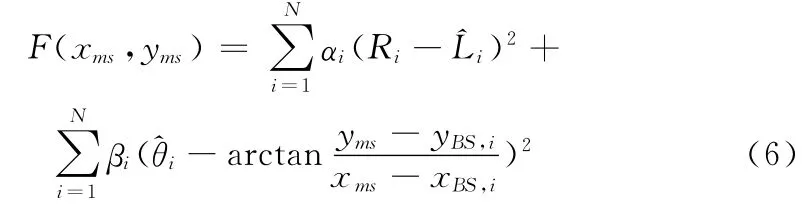
式中，Ri表示MS到BS的实际距离：

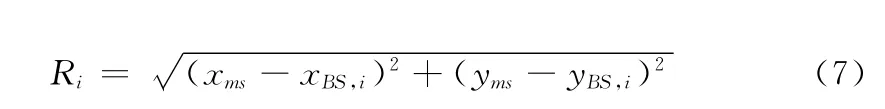
对式（6）目标函数的求解可以采用多种非线性最优化问题的求解方法，但这些方法在使用时往往需要一个较为精确的初始估计。针对上述缺点，本文算法思路如下：

如果将引起反射的散射体Si视为虚拟基站，那么利用圆周相交法可知MS的位置处于以散射体Si为圆心、半径为dms，i的圆的交点处，其中Si的坐标为：

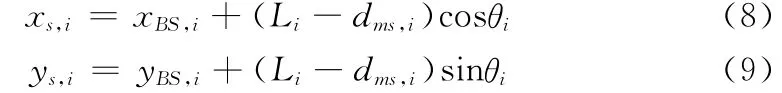
将式（8）和式（9）代入式（2）中可得MS到散射体的距离：

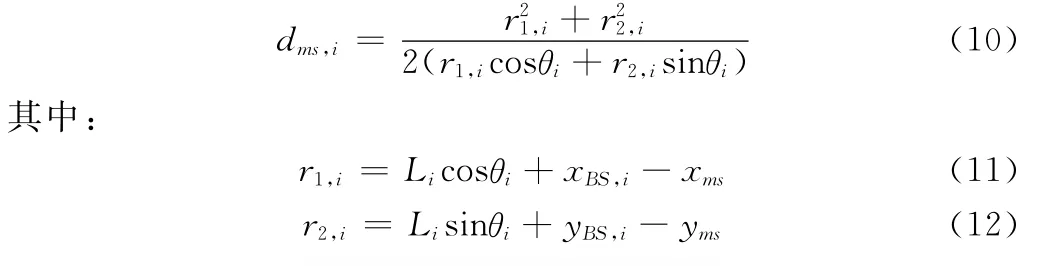
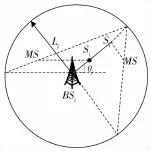
图2 移动台的可能位置

由式（10）知，只要知道MS的坐标就可以确定dms，i的大小，但MS的位置是未知的。移动台的可能位置如图2所示，在以BSi为圆心、Li为半径的圆内，每一点都可以找到对应的Si，并都能满足式（1）和式（4），使得式（5）取得最小值，但这些点对应的dms，i值却有很大不同。在单次反射圆模型中，最大散射半径为Rd，可知MS实际位置对应的dms，i满足：

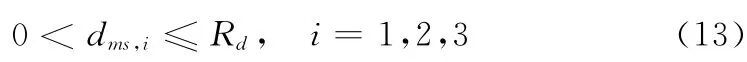
因此，在实际定位时，当测量误差较小时，若已知单次反射圆模型最大散射半径Rd（可以通过实地测量获取），可知MS位置位于以虚拟基站VBSi为圆心、半径为Rd的圆的相交部分，即图3的阴影区域。

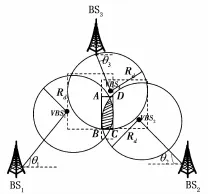
图3 移动台的位置范围

其中：虚拟基站VBSi的坐标为：

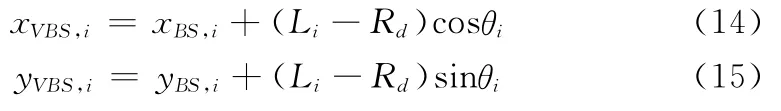
图3中的阴影区域是一个不规则图形，难以确定其位置范围，可以通过线性化的方法将其确定在矩形ABCD内，它是由3个虚拟基站构建的定位圆的相交部分所确定的最小外接矩形。故只要在矩形ABCD内找到满足式（13）的点，即可认为是MS的可能位置点。

1.2 计算过程

为了找到所有可能的MS位置点，可以使用文献［6］的GSA算法，即将MS可能范围划分成一个个网格，然后对这些网格对应的坐标进行相应计算，看是否满足式（13）。GSA算法是对整个小区扇区进行全局搜索，本文算法不同之处在于利用虚拟基站缩小了MS的位置范围，因而本文算法的定位速度要大大快于GSA算法。由于搜索到的MS可能位置点往往有多个，GSA算法认为MS估计坐标为这些点的平均值，本文为了提高定位精度，将利用式（6）对应的目标函数值的归一化倒数对MS可能位置点进行加权平均处理，步骤如下：

第一步：计算所有MS可能位置点（xk，yk）（假设总数共有M个）对应的目标函数值Fk：

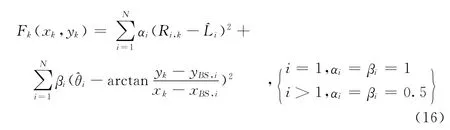
第二步：利用目标函数值Fk的归一化倒数作为权重因子，求出MS估计位置坐标：

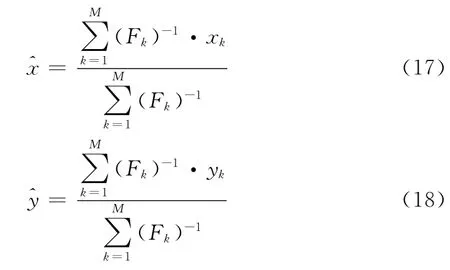
综上，本文定位算法流程为：

第一步：根据TOA、AOA的测量值确定MS的可能位置范围；

第二步：在确定的位置范围内搜索满足约束条件式（13）的所有位置点；

第三步：对这些位置点使用加权平均算法求出MS的最终估计位置。

1.3 算法中的异常情况处理

1）由于测量误差的存在，由3个虚拟基站VBSi和最大散射半径Rd构建的定位圆可能无法同时相交，即图3中的阴影区域不存在，针对这种情况，可以将MS的位置范围扩大到以基站BSi为圆心，测量距离Li构建的3个定位圆的相交部分后再行求解；若以基站BSi为圆心，测量距离Li构建的3个定位圆仍未相交，此时可以将搜索范围扩大到整个扇区。

2）同样由于测量误差，偶尔会出现一种异常情况，即在MS可能位置区域内所有点计算出来的dms，i无法同时小于Rd，即找不到满足条件的移动台可能位置点。这种情况下，可以将计算出来的dms，i3个值中两个小于Rd的点记为可能点。

2 仿真与分析

仿真过程中，小区半径R取2 000 m，基站坐标为（0，0）、，MS位置为三小区相交的1／6小区范围内任意位置。分别在不同的散射半径下仿真，每次独立测试1 000次。仿真时AOA测量误差服从标准差2°、均值为0的高斯分布；TOA测量误差服从标准差5 m、均值为0的高斯分布；搜索精度置为6 m*6 m。

图4是在单次反射圆模型下不同散射半径对应的测试结果，其中对于主基站，最大散射半径固定为150 m；对于邻近基站，最大散射半径为150～350 m。与传统的HTA算法相比，可以看出在非视距环境下，精度有了较为明显的提升；与GSA算法相比，精度也有一定程度的改善。

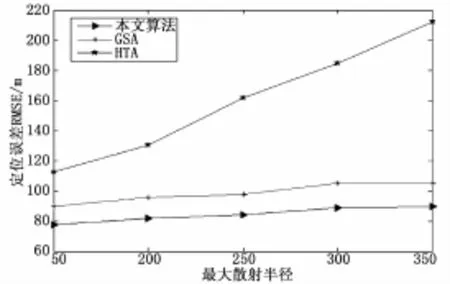
图4单次反射圆模型下不同散射半径对应的定位误差

图5 是在主基站散射半径为150 m、邻近基站最大散射半径为200 m时，3种算法的误差概率比较。其中，本文算法误差小于100 m的概率为76.7%，GSA算法对应的误差概率为69.3%，HTA算法为54.7%。仿真结果表明，在相同环境下本文算法有着更佳的定位性能。同时，本文算法由于缩小了定位范围，所以定位速度也要快于GSA算法。

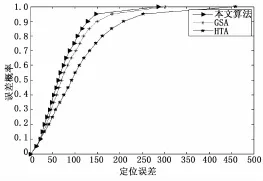
图53 种算法误差概率比较

3 结论

在单次反射圆模型的基础上，本文算法将散射体看成虚拟基站，利用移动台和散射体的位置关系确定移动台的可能位置范围。在对MS位置求解的过程中，不是通过最优化目标函数，而是直接搜索MS可能位置点，不仅摆脱了传统定位算法对初始估计的需要，而且提高了NLOS环境下的定位精度。仿真结果表明了该算法的有效性。

［1］田孝华，廖桂生.减轻TOA和AOA定位系统非视距影响的方法［J］.电子与信息学报，2003（12）：1664-1668.

［2］Venkatraman S，Caffery J.Hybrid TOA／AOA techniques for mobile location in non－line－of－sight environments［A］.Proceedings of the IEEE Wireless Communications＆Networking Conference［C］.2004，1（1）：274-278 Vol.1.

［3］Al－Jazzar S，Ghogho M，Mc Lernon D.A joint TOA／AOA constrained minimization method for locating wireless devices in nonline－of－sight environment［J］.IEEE Transactions on Vehicular Technology，2009，58（1）：468-472.

［4］黄际彦，万 群，杨万麟.基于散射体信息的双基站定位［J］.电子与信息学报，2007，29（3）：671-673.

［5］毛永毅，李明远，张宝军.一种NLOS环境下的TOA／AOA定位算法［J］.电子与信息学报，2009，31（1）：37-40.

［6］Xie Y，Wang Y，Zhu P，et al.Grid－search－based hybrid TOA／AOA location techniques for NLOS environments［J］.Communications Letters IEEE，2009，13（4）：254-256.

Study on Hybrid Location Algorithm Based on Single－Bounced Circle Model

Lu Yin，Xiang Zheng

（Nanjing University of Posts and Telecommunications，Jiangsu Provincial Key Laboratory of Wireless Communications，Nanjing 210003，China）

The existing location algorithms have low anti－Non－Line－of－Sight（NLOS）ability，and often require an accurately initial estimate during the calculation.In the single－bounced circle model，through the geometric relationships between the mobile station（MS）and the scatterers，a TOA／AOA hybrid location algorithm is proposed to suppress the NLOS error.During the process of positioning，scatterers are regarded as virtual base station（BS）.According to the maximum scatter radius，the possible location range can be determined.After seeking all points that satisfy the constraints，the weighted average method is used to improve the positioning accuracy，and the final result is the location of the mobile station.Computer simulations show the efficiency of the proposed algorithm.

single－bounced circle model；time of arrival／angle of arrival；non－Line－of－sight；virtual base station；hybrid location

1671-4598（2016）08-0203-03

10.16526／j.cnki.11－4762／tp.2016.08.055

：TN929.5

：A

2016-01-23；

：2016-04-11。

国家自然科学基金资助项目（61271236）；江苏政府留学奖学金资助项目。

陆 音（1970-），男，江苏南京人，工学博士，副研究员，副处长，主要从事无线通信方向的研究。