改进的自适应衰减卡尔曼滤波算法

高 伟，叶 攀，许伟通

（哈尔滨工程大学自动化学院，哈尔滨 150001）

改进的自适应衰减卡尔曼滤波算法

高 伟，叶 攀，许伟通

（哈尔滨工程大学自动化学院，哈尔滨 150001）

SINS／GPS组合导航系统的融合算法主要是卡尔曼滤波，卡尔曼滤波实现最优估计的前提是系统的模型和随机噪声信息必须准确已知；实际情况下，大部分系统的模型和随机噪声信息不完全可知，这可能会导致滤波器估计精度下降；针对这一问题，根据求解遗传因子的方法不同对传统的自适应衰减卡尔曼滤波进行改进，提出一种改进的自适应衰减卡尔曼滤波；改进后的算法分别适用于系统噪声统计模型不准确可知和量测噪声统计模型不准确可知两种情况，分别对应于两种滤波算法，并且二者具有统一的滤波框架；仿真结果表明，改进的自适应衰减卡尔曼滤波比卡尔曼滤波精度较高，有效解决了因为噪声模型不准确导致的精度下降问题。

组合导航系统；自适应衰减卡尔曼滤波；遗忘因子；噪声模型

0 引言

捷捷联惯性导航系统 （strapdown inertial navigation system，SINS）作为一种自主式导航系统，已经被广泛应用于舰船导航、飞机制导、水下导航等领域。GPS／SINS组合导航系统引入GPS的位置、速度信息为观测量，克服了单一SINS的误差随时间积累的缺点。

GPS／SINS组合导航系统进行数据融合时使用的是卡尔曼滤波（Kalman Filter，KF），卡尔曼滤波器是一种最优估计，但是前提是系统的模型和随机噪声信息必须准确已知。实际情况下，大部分系统的模型和随机噪声信息不完全可知，这可能会导致滤波器估计不准确甚至发散。为此，有学者提出自适应衰减卡尔曼滤波器（AdaptiveFadingKalmanFilter，AFKF）［1］，来解决系统系统噪声不完全可知的问题，但这些方法只针对系统噪声不完全可知的情况，没有考虑量测噪声不完全可知的情况，并且带有约束条件［2 3］。

针对上述问题，本章提出基于新息协方差的改进AFKF，来补偿未知的噪声信息造成的影响，改进AFKF分别适用于系统噪声不完全可知的情况和量测噪声不完全可知的情况，并且二者具有统一的滤波框架。

1 自适应衰减卡尔曼滤波算法

考虑如下线性离散时间随机系统：

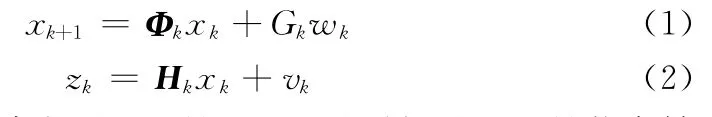
式中，xk是n×1状态矢量，zk是m×1量测矢量，Φk是状态转移矩阵，Hk是量测矩阵。系统噪声和量测噪声的序列wk、vk都是高斯白噪声，Qk、Rk为对应的方差阵。

为了补偿不完整噪声信息的影响，将遗忘因子λk引入误差协方差方程，形式如下：

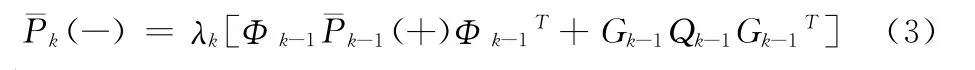
定义1：

对于式（1）表示的线性随机系统，系统噪声统计模型不完整的情况，其离散时间自适应衰减卡尔曼滤波器（AFKF）［4］为：

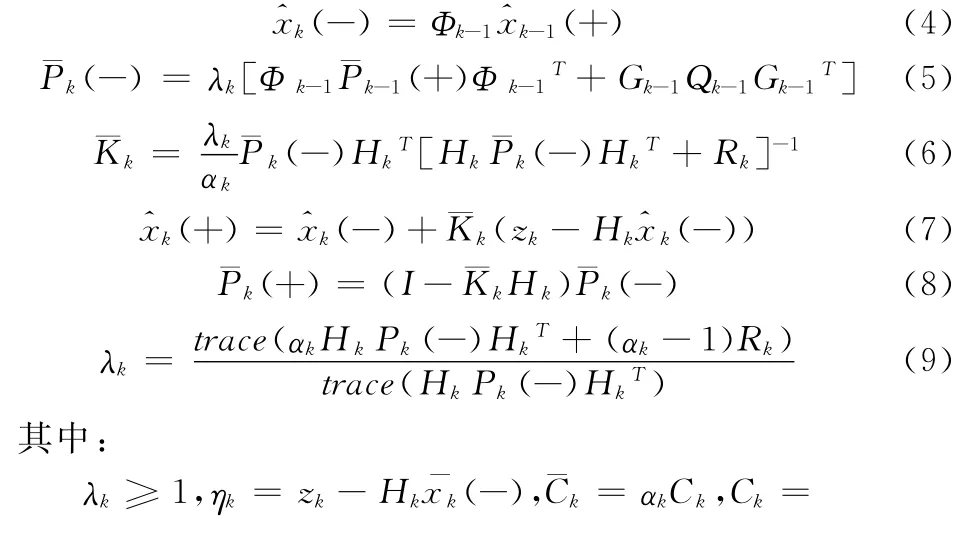
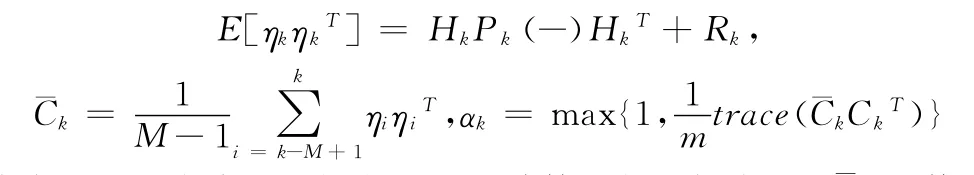
式中，ηk是滤波器的新息，Ck是计算的新息协方差，¯Ck是估计的新息协方差，M是窗口尺寸，Pk（－）是计算的KF的误差协方差。

2 改进的自适应衰减卡尔曼滤波算法

式（9）成立的前提条件是HkT列满秩，并且只针对系统噪声不完全可知的情况，为了避免这些限制，对求解遗忘因子的方法进行改进，提出改进的自适应衰减卡尔曼滤波。

当前时刻的新息协方差的估计值：

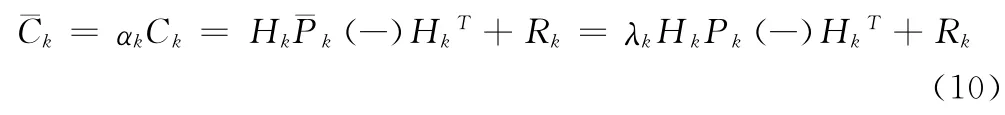
新息主要由误差决定，新息协方差可以很好地反应当前时刻误差的影响，因此未知的系统噪声信息会使误差协方差和新息协方差都增加。在式（4）中量测方差Rk保持不变，这表明αk表征的新息协方差的增加是由λk表征的误差协方差的增加导致的。Pk（－）的增加量可以补偿系统噪声信息不完整产生的影响，如果增加的误差协方差大于Rk，可以认为αk近似等于λk。那么，称这种AFKF为“调谐Pk的 AFKF”。

对于量测方程不完整的情况，同上述情况一样，未知的量测方程信息会使误差协方差和新息协方差都增加。这种情况下可以认为αk表征的新息协方差的增加是由量测噪声协方差Rk的增加导致的，误差协方差Pk（－）保持不变。Rk的增加导致Kk的减少，Kk的减少量可以补偿未知的量测方程信息产生的影响。假设取λk＝1，则误差协方差保持不变¯Pk（－）＝Pk（－）。设计滤波器的增益变为原来的，滤波增益的减小意味着更少的利用量测信息，滤波增益的减少使量测噪声协方差Rk变为αkRk，如式（5）所示。称这种AFKF为“调谐Rk的AFKF”。第二种方法得到的滤波增益为：

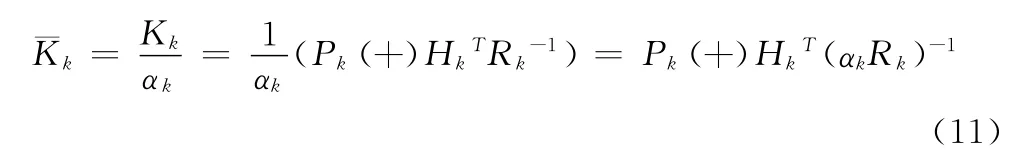
定义2：

对于式（1）表示的线性随机系统，系统噪声不完全可知的情况，即调谐Pk的AFKF，其离散时间自适应衰减卡尔曼滤波器（AFKF）与定义1比较，需要把式（5）、（6）换成式（12）、（13）：

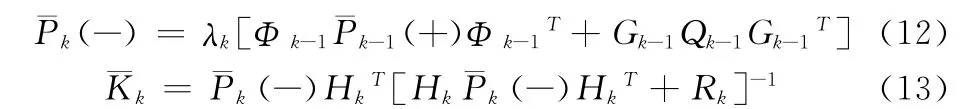
定义3：

对于式（1）表示的线性随机系统，量测噪声不完全可知的情况，即调谐Rk的AFKF，其离散时间自适应衰减卡尔曼滤波器（AFKF）与定义1比较，需要把式（5）、（6）换成式（14）、（15）：

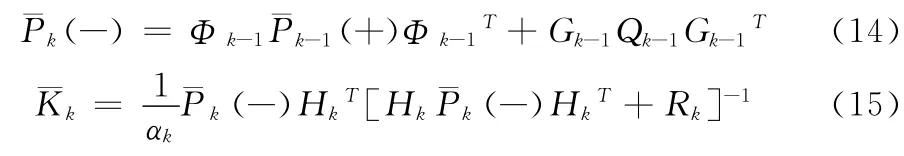
图1表示的是改进的AFKF的原理，该AFKF为系统噪声信息不完整和量测噪声信息不完整两种情况提供了统一的滤波框架，利用新息求解的遗忘因子能够自动适应并补偿未知信息造成的影响。同时，该算法计算量较小，遗忘因子的计算较简单，能够应用于比较复杂的线性随机系统。

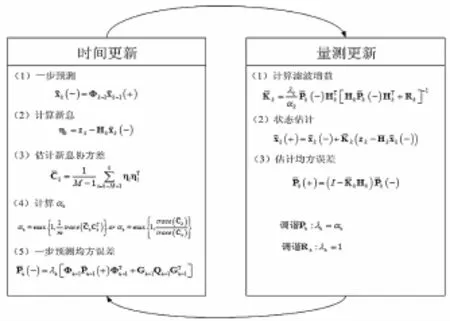
图1 AFKF原理框架图

3 滤波模型

利用AFKF对系统的参数进行估计时，首先要建立状态方程和量测方程，具体过程如下：

将加速计零偏和陀螺漂移扩展至状态量中，状态方程基本形式为：

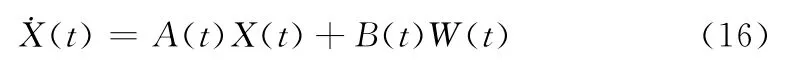
式中，状态量为：

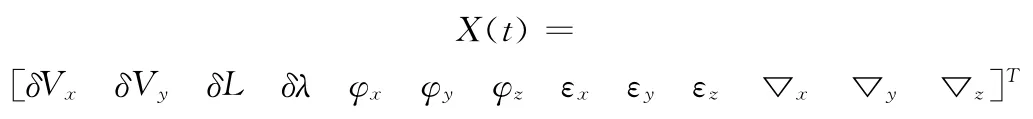
状态矩阵为：

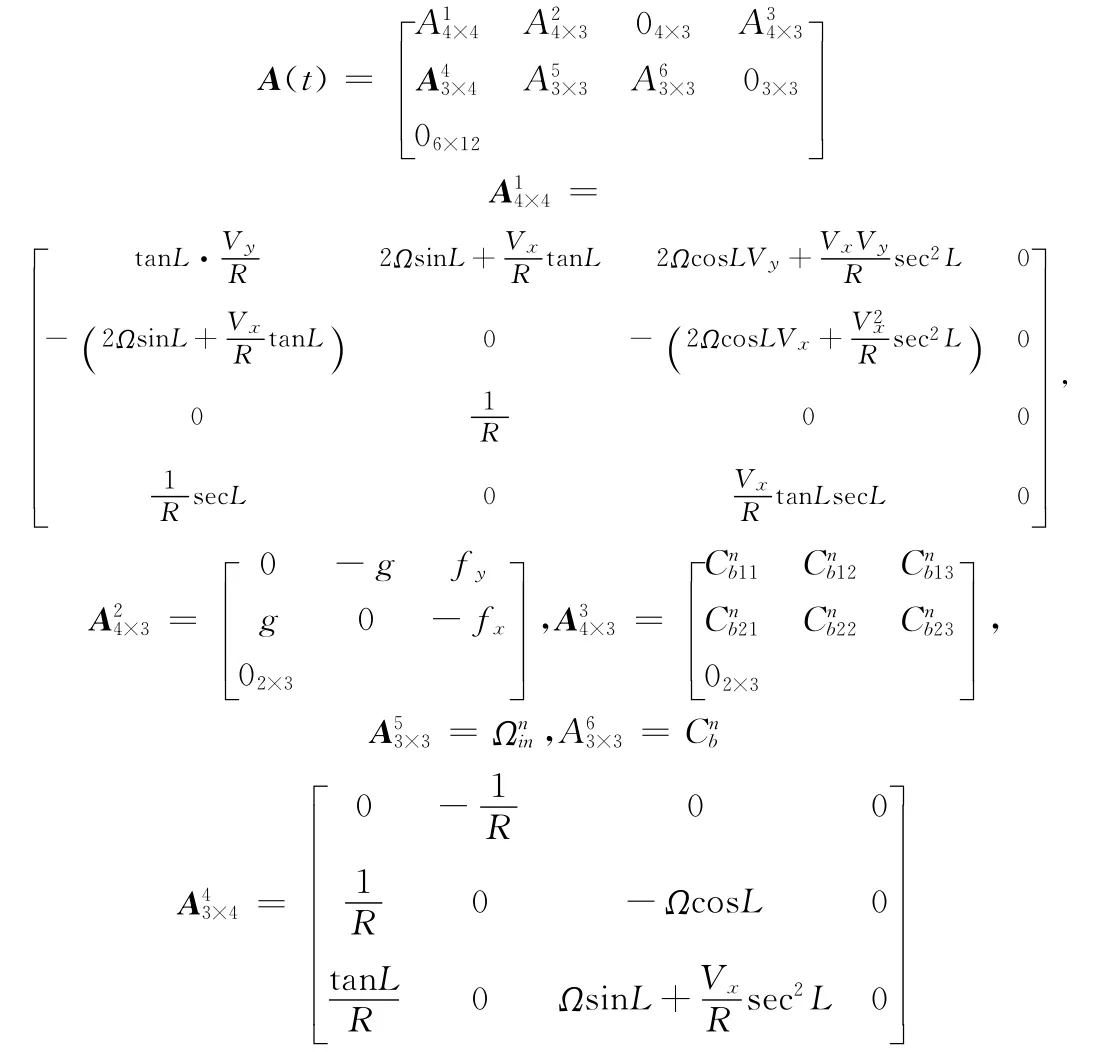
选取惯导解算的位置与GPS提供的位置的差值作为观测量，量测方程为：

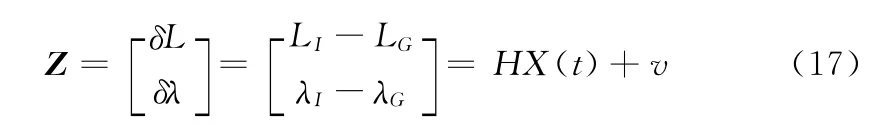
式中，H＝［02×2diag（1，1） 02×3］；LI、λI为惯导的解算值；LG，λG为GPS测量值。

4 仿真分析

仿真初始条件设置如下：

1）陀螺和加速度计的输出信号由捷联惯性导航系统模拟器产生，陀螺常值漂移为0.01°／h，加速度计常值零偏为10－4g；系统噪声和测量噪声均设为高斯白噪声。

2）卡尔曼滤波的初始条件：X（0）各分量都取0；

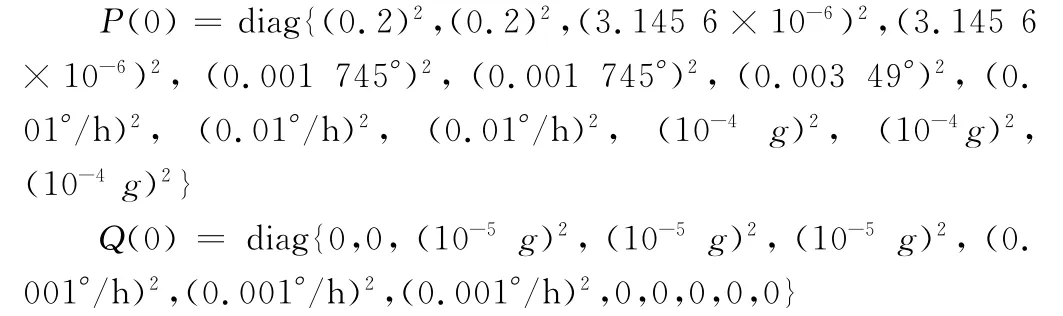
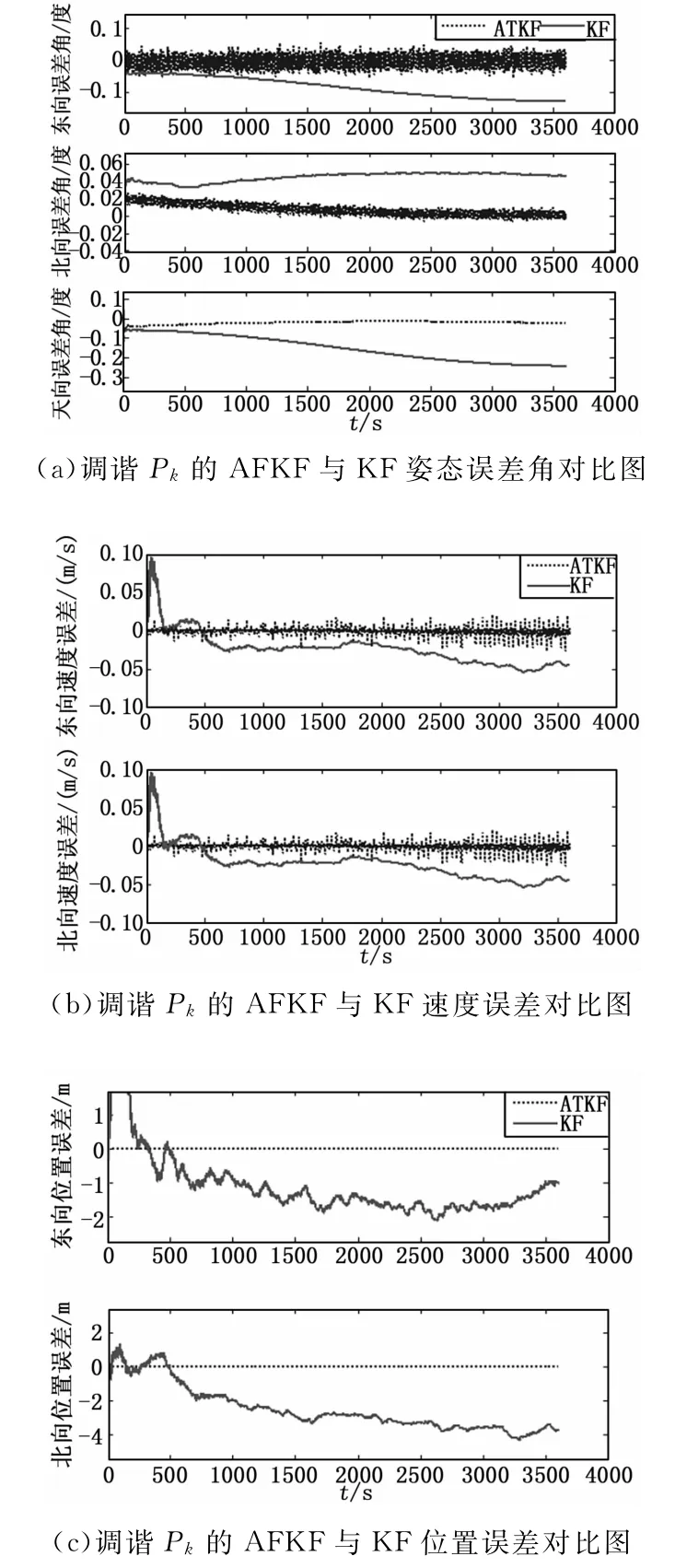
图2 误差对比图

3）载体以Vx＝2 m／s，Vy＝2 m／s的速度匀速直行；导航开始阶段初始姿态角误差：0.05°，0.05°，0.1°；初始经度λ＝126.670 5°，初始纬度L＝45.779 6°。

设测量噪声完全可知，系统噪声不完全可知，则基于调谐Pk的AFKF的SINS／GPS组合导航系统仿真结果如图2所示。

从图2可以看出，与KF相比基于调谐Pk的ATKF的SINS／GPS组合导航系统导航参数收敛较快，收敛精度较高，尤其是位置误差达到了很高的精度。

在相同仿真条件下，设系统噪声完全可知，测量噪声不完全可知，则基于调谐Rk的AFKF的SINS／GPS组合导航系统仿真结果如图3所示。

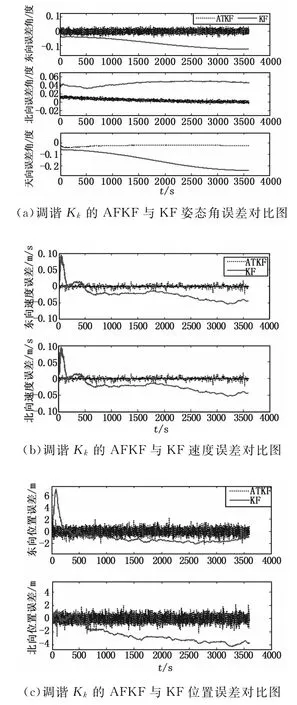
图3 误差对比图

从图3可以看出，与KF相比基于调谐Rk的AFKF的SINS／GPS组合导航系统导航参数收敛较快，但位置误差的收敛精度相比于基于调谐Pk的AFKF较低，这是由于位置噪声的统计信息不准确可知导致的，但相比于KF收敛精度较高。

5 结论

为了解决SINS／GPS组合导航系统中噪声统计信息不完整造成的影响，提出改进的自适应衰减卡尔曼滤波。改进的算法简化了遗忘因子的求解，可以分别适用于系统噪声不完全可知和量测噪声不完全可知两种情况，并且二者具有统一的滤波框架。对算法的仿真结果表明，改进的算法可以很好的补偿噪声信息不完全可知造成的影响，对提高SINS／GPS组合导航系统的导航精度有实际的意义。

［1］Kim KH，Lee J G，Chan G P.Adaptive Two－Stage Extended Kalman Filter for a Fault－Tolerant INS－GPS Loosely Coupled System［J］.IEEE Transactions on Aerospace＆Electronic Systems，2009，45（1）：125-137.

［2］Hu Y M，Qin Y Y.Notice of Retraction Adaptive two－stage Kalman filter in the presence of random bias［A］.2010 3rd IEEE International Conference on Computer Science and Information Technology（ICCSIT）［C］.IEEE，2010.

［3］Kim K H，Lee J G，Chan G P.Adaptive two－stage Kalman filter in the presence of unknown random bias［J］.International Journal of AdaptiveControl＆Signal Processing，2006，20（7）：305 -319.

［4］Hide C，Moore T，Smith M.Adaptive Kalman filtering algorithms for integrating GPS and low cost INS［A］.Position Location and Navigation Symposium 2004［C］.2004：227-233.

Improved Adaptive Fading Kalman Filter Algorithm

Gao Wei，Ye Pan，Xu Weitong

（Automation College，Harbin Engineering University，Harbin 150001，China）

The fusion algorithm of SINS／GPSintegrated navigation system is mainly based on Kalman filter.Kalman filter is the optimal estimation on the conditions that system model and random noise information are accurately known.In practice，most system model and random noise information are not completely known，which may lead to filter estimation accuracy decline.Aiming at this problem，this paper improves the traditional adaptive fading Kalman filter according to the method of solving forgetting factor，and proposes an improved adaptive fading Kalman filter.The improved algorithm respectively applies in the cases that system noise statistical model cannot be accurately known and measurement noise statistical models cannot be accurately known，respectively corresponding to the two filter algorithms.What’s more，they have a unified filter framework.The simulation results show that the improved adaptive fading Kalman filter is more accurate than Kalman filter and it can effectively solves the accuracy decline problem caused by the inaccurate noise model.

integrated navigation system；adaptive fading Kalman filter；forgetting factor；noise model

1671-4598（2016）08-0190-03

10.16526／j.cnki.11－4762／tp.2016.08.051

：U666.1

：A

2016-01-16；

：2016-02-11。

国家自然科学基金（51379042）；中央高校基本科研业务费专项资金（heucfq1404）。

高 伟（1977-），男，黑龙江哈尔滨人，博士，教授，主要从事捷联导航技术、光学陀螺技术、海洋运载器综合导航技术方向的研究。