全相位FFT在导弹自动驾驶仪测试中的应用
2017-01-13琼1何云东2虎3
李 琼1,2,何云东2,秦 虎3
(1.上海交通大学电子信息与电气工程学院,上海 200240;2.上海机电工程研究所,上海 201109;3.中国人民解放军驻上海航天局中心军事代表室,上海 201109)
全相位FFT在导弹自动驾驶仪测试中的应用
李 琼1,2,何云东2,秦 虎3
(1.上海交通大学电子信息与电气工程学院,上海 200240;2.上海机电工程研究所,上海 201109;3.中国人民解放军驻上海航天局中心军事代表室,上海 201109)
自动驾驶仪是导弹的姿态控制系统,其性能好坏决定了导弹飞行的稳定性。为了精确测量其性能,对导弹自动驾驶仪测试原理和方法进行了研究,进行了正弦信号测量方法的分析,提出了基于全相位FFT数据处理方法,并结合时移相位差校正方法实现正弦形式信号的频率、幅度和相位等参数的精确测量;利用Lab VIEW图形化编程软件设计了算法软件,通过仿真试验考察了该算法在无噪、低噪和大噪环境下信号测量精度,结果表明全相位FFT方法在信号频谱测量方面具有精度高、抗噪能力强等优点,满足自动驾驶仪的测试需求。
自动驾驶仪;全相位快速傅氏变换;时移相位差
0 引言
自动驾驶仪是导弹制导控制系统的重要组成部分,其主要功能是保证导弹的稳定飞行,接受程控或制导指令,稳定和控制导弹的质心运动及绕质心的角运动,控制导弹付出相应的侧向过载或控制导弹姿态角。在导弹出厂测试项目中,自动驾驶仪的测试尤为重要,通常利用动态激励装置产生正弦运动激励,来实现自动驾驶仪的性能测试。
本文在详细分析了某型号导弹自动驾驶仪和激励测试设备的原理基础上,根据全相位FFT数据处理[1-2]和时移相位差校正法[3-4]的算法思想,采用Lab VIEW图形化编程工具开发自动测试软件,实现了自动驾驶仪测试信号的频率、幅度和相位差等参数的测量。本文针对软件进行了无噪、低噪和大噪环境下的仿真试验,结果表明该软件的测量精度高,并具有良好的抗噪性能。
1 自动驾驶仪的原理和测试方法
1.1 自动驾驶仪的原理
自动驾驶仪由惯性测量组合,控制组合和执行机构组成,导弹角速度与线加速度信息由惯性测量组合实时测量并给出数字量;控制组合由控制计算机及其解算软件组成,通过测量信号与控制指令等综合后,进行控制律运算形成舵指令,输出至执行机构(舵系统)控制导弹运动,舵系统的输出用舵反馈信号表示。自动驾驶仪的一般工作原理如图1所示。
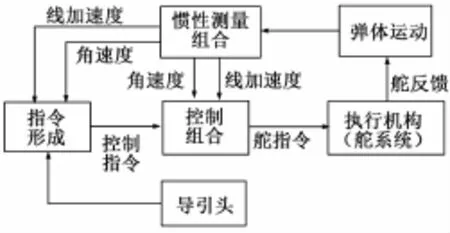
图1 自动驾驶仪工作原理框图
自动驾驶仪作为导弹制导控制系统的一个重要组成部分,在系统中起着非常关键的作用。导弹弹体执行坐标系为OX1aY1aZ1a,沿OY1a、OZ1a方向的过载控制通道分别为Ⅰ、Ⅱ通道,沿OX1a方向的滚转角控制通道为Ⅲ通道,舵面安装在弹体执行坐标系上,如图2。
一方面,惯性测量组合测得的滚动角信号和Ⅲ通道的角速度传感器测得的角速度信号按周期实时送给控制组合舵系统一个稳定弹体的舵指令,舵系统执行舵指令后偏转使导弹的滚动角维持在规定的精度范围内;另一方面,根据Ⅰ、Ⅱ通道的角速度和线加速度传感器敏感到的角速度信号和过载信号,与导引头的指令综合,形成舵指令传给舵系统,控制导弹向目标飞行。
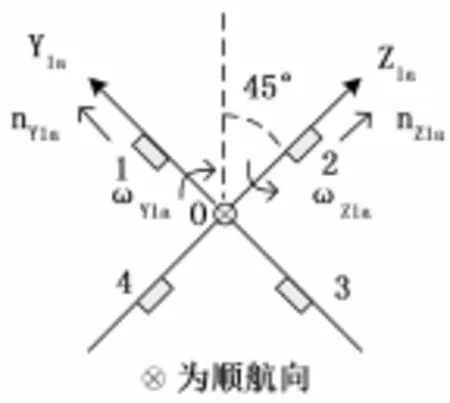
图2 弹体执行坐标系示意图
1.2 自动驾驶仪的测试方法
在防空导弹测试中,通常采用动态激励装置对导弹内惯性测量装置的敏感元件分别给予一定变化规律的动态激励,以测试控制系统的工作性能[5]。对于小型导弹,在总装和综合测试时,一般将舱段状态或全弹状态放在动态激励装置上进行摇摆(滚动)激励。这种动态激励装置一般称为摇摆台。
摇摆台选用正弦机构产生正弦信号,其表达式为:

式中,Θ0为摆幅最大值;ω=2πf。
运动速率为:
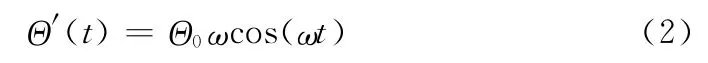
自动驾驶仪测试时,导弹呈“×”型水平放置在摇摆台上并固定,控制摇摆台作摇摆运动以对驾驶仪Ⅰ、Ⅱ通道的性能进行测试,控制摇摆台作滚动运动以对Ⅲ通道的性能进行测试,导弹摆放如图3所示。
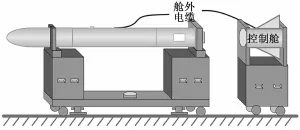
图3 导弹测试摆放示意图
Ⅲ通道测试时,摇摆台绕OX1a轴线做滚动运动,该轴线上敏感到的角速度ωX1a为摇摆台运动的角速度Θ′(t)。Ⅰ、Ⅱ通道测试时,摇摆台绕竖直方向做左右摇摆运动,OY1a、OZ1a轴线上敏感到的角速度ωY1a、ωZ1a为Θ′(t)cos45°。控制组合实时接收惯性测量组合发送过来的角速度信号,形成对应的余弦信号形式的舵指令,舵系统(4个舵)执行相应的舵指令使舵偏转,输出反映舵偏转大小的舵反馈信号。通过测量舵反馈信号的频率、幅值及其与角速度信号的相位差,即可测出3个通道的控制性能参数,从而实现自动驾驶仪的自动测试。
2 全相位FFT原理
全相位数据处理是由天津大学王兆华教授和侯正信教授提出的一种数字信号处理的新方法,因其在频谱校正上有很高的精度和良好的抗噪性能,目前已在电力系统谐波分析、铁道信号频率检测、介损测量、雷达测速、激光测距等方面均有应用[6 8]。全相位FFT的一般流程是先将数据进行全相位预处理,然后再进行FFT。
假设数据长度为2 N-1的序列x[n]:n=0,1,…,2N-2,对其进行全相位数据预处理的第一步:列出包含序列中心点x [N-1]的所有长度为N的序列xi[n]:i,n=0,1,…,N -1,共形成N个序列:
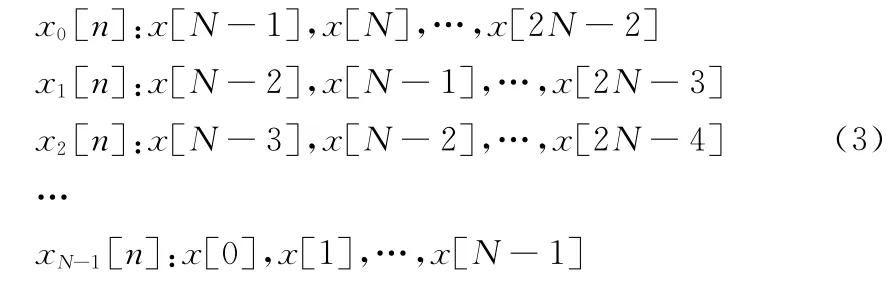
依次将序列xi[n]向左循环移位i位得到新的序列x′i[n]:i,n=0,1,…,N-1,形成x[N-1]都在首位的N个序列。
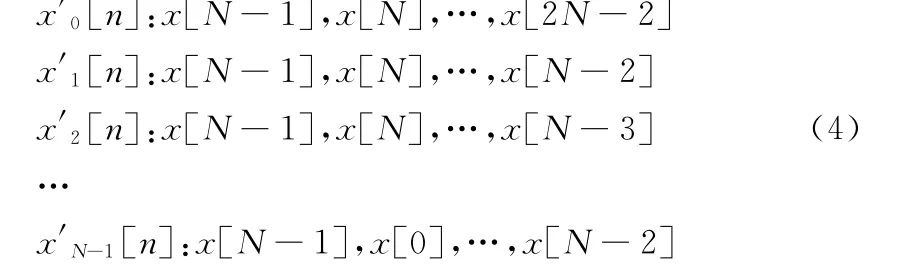
将序列x′i[n]相同位置的数据求和得到长度为N的序列y[n]:n=0,1,…,N-1。
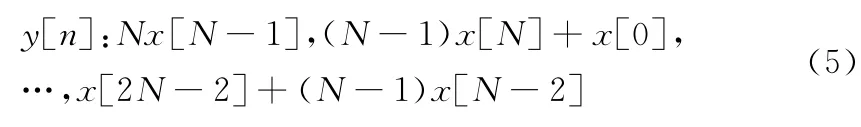
上述全相位数据预处理过程相当于用均为矩形窗RN[n]的前窗f[n]和后窗b[n]分别对序列xi[n]、x′i[n]进行处理得到预处理后的数据序列。数据处理的具体步骤为:
1)用前窗f[n]对序列xi[n]进行加窗处理得到加窗后的序列xfi[n]=f[n]xi[n];
2)将xfi[n]进行循环移位得到序列x′fi[n]=xfi[(n+i)N];
3)用后窗b[n]对x′fi[n]相同位置的数据进行加权后求和得到序列。
当f[n]和b[n]均为矩形窗时,数据处理称为无窗全相位数据预处理;当其中一个为非矩形窗时,数据处理称为单窗全相位数据预处理;当两个均为非矩形窗时,数据处理称为双窗全相位数据预处理[1]。
下面研究单频复指数序列:

式中,A为信号幅值,ω0为序列的数字角频率,φ0为序列的初始相位值。
根据FFT移位性质,x′fi[n]的傅里 叶变 换X′fi[k]和xfi[n]的傅里叶变换Xfi[k]有如下关系:
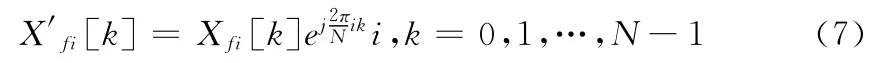
对式(7)进行求和即为全相位FFT的输出:
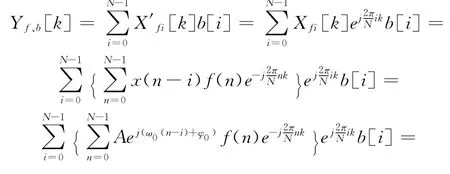
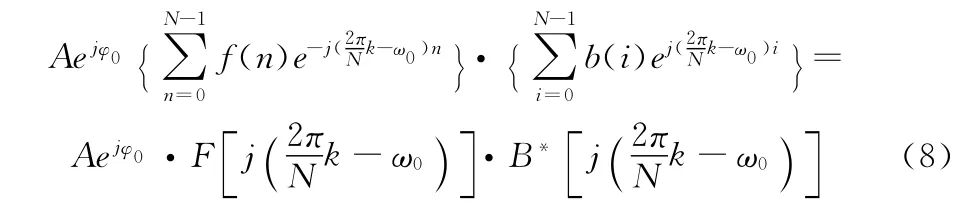
3 全相位时移相位差法的原理
在3种全相位FFT方式中,双窗全相位FFT在频谱估计精度和抗噪性能的综合性能最好[2],下面研究序列{x1[n]=Aej(ω0n+φ0),n∈[-N+1,N-1]}和延时n0后的序列{x2[n]=Aej[ω],n∈[-N+1,N-1]}的相位谱变化情况,在前窗f[n]和后窗b[n]均不是矩形窗(f[n]=b[n])的基础上讨论全相位时移相位差法的原理。
由式(8)可求得序列 {x1[n]=Aej(ω0n+φ0),n ∈[-N +1,N-1]}的双窗全相位FFT谱分析的表达式为:
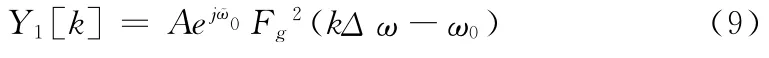
则其主谱线k0上的相位谱表达式为:

根据全相位FFT谱分析的线性性质,延时n0后的序列{x2[n]=Aej[ω],n∈[-N +1,N -1]}的双窗全相位FFT谱分析的表达式为:
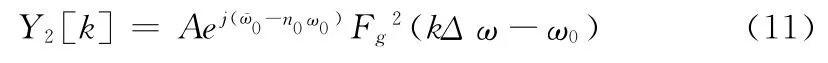
则其主谱线k0上的相位谱表达式为:

取式(10)与式(11)的差值,得:
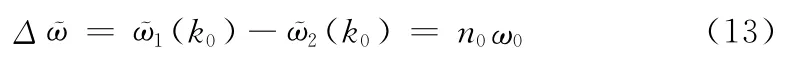
因此可得到信号频率的估计公式:

从式(14)可以看出,具有延时关系的两序列主谱线上的相位差Δφ与延时大小n0成正比,n0越大则Δφ越大。但实际信号处理时,由主谱线的实部和虚部计算得到的相位值在有限的[-π,+π]范围内,因此实际测量得到的相位差Δφ被限定在[-2π,+2π]范围内,与理想值不同。为了消除这种差异,需要对测量得到的相位差进行补偿:主谱线k0处对应的数字角频率为2 k0π/N,经过大小为n0的延时后,这个数字角频率会引起2 n0k0π/N的附加相移[6]。因而,对于主谱线k0处经过相位补偿后得到的相位差表达式为:
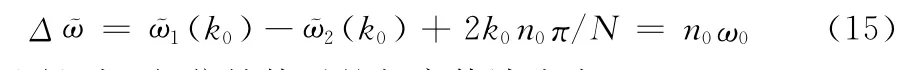
因此得到经相位补偿后的频率估计公式:
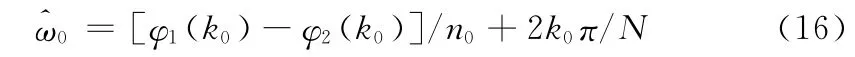
由式(16)得到主谱线k0上的频偏值dω为:
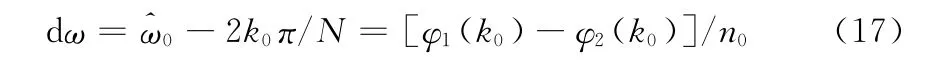
在得到主谱线上的频偏值dω后,根据式(9)可以得到信号的幅度估计公式:

4 自动驾驶仪测试软件实现和仿真试验
4.1 软件实现
在驾驶仪测试时,软件控制A/D信号采集板卡以采样率fs对导弹敏感到的摇摆台运动角速度(ωX1a、ωY1a和ωZ1a)和4个舵反馈信号进行采样,得到一段时间的测试信号数据。将待测的舵反馈信号和对应角速度测试基准信号数据序列进行全相位FFT数据处理和分析,计算得出舵反馈信号的幅值和频率,以及舵反馈信号和基准信号间的相位差值,软件框图如图4。
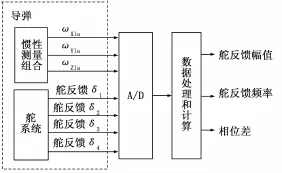
图4软件框图
图4 中的数据处理和计算部分是软件的核心,软件基于NI公司图形化编程开发软件Lab VIEW实现全相位时移相位差法并进行数据处理和计算。软件对起始采样时刻相同并具有相同样本数的角速度信号和舵反馈信号进行数据分段和预处理,下面以舵反馈信号δ1和角速度信号ωX1a的测量为例来说明软件的具体实现思路。
软件首先获取待处理的舵反馈信号δ1的数据长度L,(L+1)/3向下取整后得出全相位数据长度N,从第一个数据样本起选取总长度为3N-1的数据序列δ1[n](n=0,1,…,3N-2)。选取数据序列δ1[n]具有延时N大小关系的两组长度均为2N -1的序列:{序列1:δ1[n](n=N,N+1,…,3N-2)}和{序列2:δ1[n](n=0,1,…,2N-2)}。对序列1和序列2分别进行双窗全相位FFT处理,得到其主谱线上的相位φ1和φ2,计算出序列1和序列2的相位差Δφ,从而得到主谱线处的频偏值dω =Δφ/N,根据式(16)可以计算出舵反馈信号δ1的数字角频率ω1,数字角频率ω1和信号频率f1的转换关系公式为:
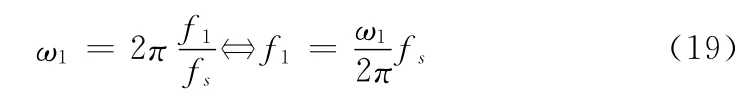
式中,fs为信号的采样频率。
由于待测信号均为余弦形式的信号,信号幅值的公式需稍作改变。考虑余弦形式的信号A cos(ω0n+φ0),可将它转换成以下两个复指数形式的信号之和:
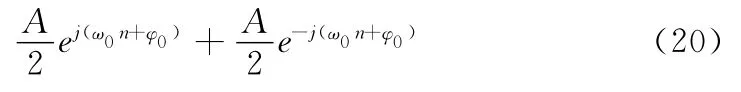
由式(20)可以看出,余弦信号由正负频率的两个复指数信号组成,根据全相位FFT的线性性质可知,频谱图上正频率部分对应的主谱线k0处的幅度值与幅值A存在以下关系:
式中,Fg(ω)为所选窗函数对应的幅度谱表达式。
本软件选用双Hanning窗全相位FFT,Fg(ω)的表达式是确定的,主谱线k0处的幅度值|Y[k0]|也很容易求得,因而可以根据式(21)的关系式计算出信号的幅值A。
对同一时间段长度同样为L的角速度信号ωX1a的数据进行同样的处理,得到长度为2 N-1的序列ωX1a[n](n=N,N +1,…,3N-2),对该序列进行双窗全相位FFT处理,得到其主谱线上的相位φ3,计算φ1和φ3的差值即可得到舵反馈信号δ1与角速度信号ωX1a的相位差值。
4.2 软件仿真实验
下面利用Lab VIEW编写软件仿真试验程序,对软件的信号测量性能进行分析和验证,试验程序前、后面板如图5、图6所示。
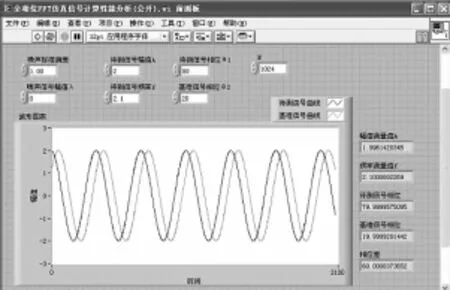
图5 全相位FFT仿真试验程序前面板
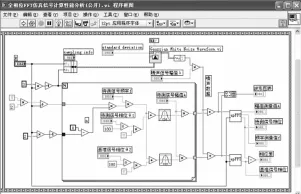
图6 全相位FFT仿真试验程序后面板
假设谱分析的阶数为N=1 024,对混有噪声的复合余弦信号进行分析,信号表达式为:
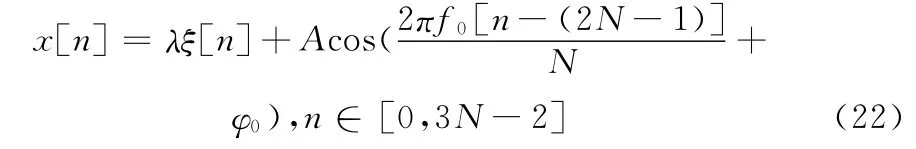
式(22)中,ξ[n]是均值为0,方差为1的高斯白噪声,通过改变参数“λ”值来调节噪声幅值。为方便分析,仿真程序中将待测信号(模拟舵反馈信号)和基准信号(角速度信号)的幅值A都设置为2.0,两信号的频率f0大小依次设置为1.0 Hz、2.1 Hz、5.2 Hz、10.5 Hz,两信号的初始相位设定为不同值。当λ分别取0、0.5、2时,对应信噪比分别为+∞、15 dB、3 dB,模拟无噪、低噪和大噪环境。试验过程运用蒙特卡罗方法进行了100次模拟,软件测量得到的待测信号频率f0、待测信号幅值A、待测信号初始相位φ1、基准信号初始相位φ2以及两信号的相位差Δφ的结果如图7。
上述仿真试验中,全相位FFT分析采用汉宁双窗处理信号数据,频率分辨率Δf=1 Hz,序号1至序号4所测信号频率的频偏分别为0、0.1Δf、0.2Δf、0.5Δf。从表1的试验结果可以看出,软件在无噪的环境下测量的频率和相位值精度很高,频率测量误差达到10-6以下,相位测量误差达到10-4度以下,幅值测量误差达到0.2%以下。随着噪声的增强和信号频偏增大,信号测量的误差也增大,但频率最大测量误差在1%左右,相位最大测量误差小于1°,幅值最大测量误差在2.6%左右。因此,该软件采用的全相位FFT分析方法在信号频谱测量方面具有精度高、抗噪能力强等优点,满足自动驾驶仪的测试需求。
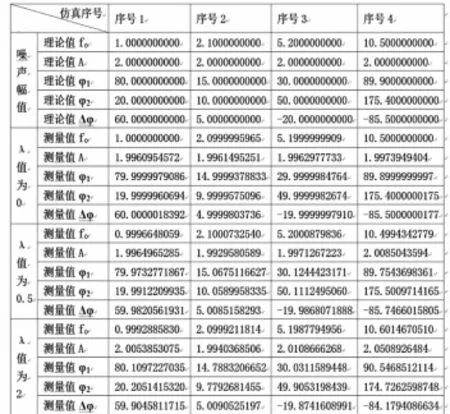
图7 软件仿真测量信号频谱性能分析
5 结论
本文从某型号导弹自动驾驶仪测试设备的特点出发,介绍了自动驾驶仪的测试需求、原理和方法,并着重分析了全相位FFT分析方法和时移相位差校正法。本文利用Lab VIEW图形化编程软件实现了基于全相位FFT分析算法的自动驾驶仪测试软件,并编写了仿真程序对该软件的计算性能进行仿真试验,验证结果表明该软件可以满足该导弹自动驾驶仪性能的测试。
[1]王兆华,黄翔东.基于全相位谱分析的相位测量原理及其应用[J].数据采集与处理,2009,24(6):777-782.
[2]王兆华,侯正信,苏 飞.全相位FFT频谱分析[J].通信学报,2003,24(11A):6-19.
[3]黄翔东,王兆华.全相位时移相位差频谱校正法[J].天津大学学报,2008,41(7):815-820.
[4]张 涛,任志良,陈 光,等.改进的全相位时移相位差频谱分析算法[J].系统工程与电子技术,2011,33(7):1468-1472.
[5]翟 超,杨志峰,李小兵.导弹自动驾驶仪测试系统的开发研究[J].计算机测量与控制,2007,15(12):1745-1747.
[6]黄翔东,王兆华.全相位FFT相位测量法的抗噪性能[J].数据采集与处理,2011,26(3):286-291.
[7]Fan X Z,Yan X L.DFT accurate amplitude,phase and frequency analysis method[A].2011 Second International Conference on Mechanic Automation and Control Engineering(MACE)[C].2011:1233-1236.
[8]齐国清.几种基于FFT的频率估计方法精度分析[J].振动工程学报,2006,19(1):86-92.
Application of All-phase FFT Method in Test of Missile Autopilot
Li Qiong1,2,He Yundong2,Qin Hu3
(1.School of Electronic Information and Electrical Engineering,Shanghai Jiaotong University,Shanghai 200240,China;2.Shanghai Eletro-Mechanical Engineering Institute,Shanghai 201109,China;3.Military Representative Office of Chinese people's Liberation Army in Shanghai Space Agency,Shanghai 201109,China)
Autopilot is the attitude control system of missile,whose performance determines the stability of the missile flight.In order to accurately measure the performance of the missile autopilot,its testing principle and method are studied.The data processing method based on all phase FFT is proposed,with the analysis of methods of measuring sine signal.It realizes the accurate measurement of the parameters of sinusoidal signals in the form of frequency,amplitude and phase,combined with the time shift phase difference correction method.The software algorithm is designed,using the Lab VIEW graphical programming software.The measurement accuracy of the algorithm in noise free,low noise and environmental noise signal is investigated through the simulation experiment.The all phase FFT method has high precision and strong anti noise ability in terms of signal spectrum measurement,which satisfy the test requirements of missile autopilot.
autopilot;ap FFT;time-shift phase difference
1671-4598(2016)08-0141-04
10.16526/j.cnki.11-4762/tp.2016.08.038
:TJ760
:A
2016-03-06;
:2016-03-27。
李 琼(1985-),男,湖南衡阳人,大学,主要从事导弹测试系统设计方向的研究。
