基于多维状态参量和时间序列对电机的异常检测

徐守坤，瞿诗齐，石 林，王 斌

（常州大学信息科学与工程学院，江苏常州 213000）

基于多维状态参量和时间序列对电机的异常检测

徐守坤，瞿诗齐，石 林，王 斌

（常州大学信息科学与工程学院，江苏常州 213000）

针对传统对电机的异常检测常常出现误判或滞后的情况，采用基于时间序列对电机单一状态参量用AR拟合，同时利用SOM神经网络无监督的方式量化电机数据；然后，利用得到的量化序列结合AR曲线得到序列的转移概率，及早发现某种状态参量的异常变化；之后，DBSCAN算法挖掘多维参数之间特征关系来确定电机是否出现异常；最后结合实例说明该方法的检测过程，并对比验证了该方法的优越性。

异常检测；时间序列；AR拟合；SOM神经网络；DBSCAN算法

0 引言

现在对于电机故障发生前的异常检测成为了必然的研究趋势，对设备进行异常检测大多是根据经验对电机部分状态参量设置的阈值，或者利用神经网络训练等人工智能的方式来检测异常［1］。这些传统的检测方式，不仅存在着数据分析片面性的问题，而且由于异常数据少，数据之间的相关性复杂等问题不能很好的建立比较完善的异常检测模型。近年，大数据技术中时间序列分析法［2］、隐马尔科夫算法［3］、聚类算法［4］等也被引入了设备异常检测领域，为电机的异常检测提供了新的思路［5］。但是，这些单一的方法对电机异常的检测，容易出现误判或者判断滞后的情况，不能及时高效地进行异常判定。

本文考虑电机运行时状态参量与时间序列的相关性，提出通过时间序列分析和无监督学习的方式，来对电机进行异常检测。针对电机正常的单一状态参量，通过时间序列的自回归算法［6］和利用自组织神经网络［7］分别拟合建立电机的时间序列模型；然后利用训练好的自组织神经网络量化数据，根据建立好的AR模型［8］，得到监测数据基于时间轴的转移概率序列。同时，将设备的多种状态参量通过DBSCAN聚类算法［9］来处理它们之间的复杂关系，从而建立电机的异常检测模型。该方法通过时间序列模型和自适应模型来挖掘数据的特征，尽早发现异常的出现，同时利用DBSCAN的方法来综合多维状态参量的关系，解决单一状态量的片面性从而减少误判。与传统的阈值判定、神经网络训练和单一的聚类的方法的方式相比而言，该方法不仅解决了多维参量的相关性和异常数据少的问题，而且还增加了异常判定的准确性。

1 相关算法

1.1 时间序列自回归模型

时间序列自回归模型（Auto－Regressive，AR）就是按照时间的顺序，分析数据序列本身的规律和特征，从而预测该数据未来的情况。简言之，利用时间轴上已知的数据，用统计学的方法来预测未来的数据。因为AR系统中数据的变化依赖于上时刻的数据［10］，不会发生突变，这与企业中电机运行时的低动态性相符合，所以比较适合对电机进行拟合。

电机在正常工作时，状态量主要呈现平稳状态或者周期性变化。其中变化不大的数据序列因其势态比较平稳，可直接用AR（1）拟合，如：电机的三相电压电流、功率因素等；周期性变化的数据序列，总的来说波动幅度不大，如电机温度、振动、噪声等，在除掉周期性后也可以通过AR（1）拟合，公式如下：

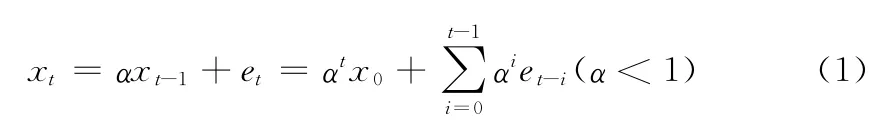
其中：xt为设备状态参量的数据序列；et为正态分布的白

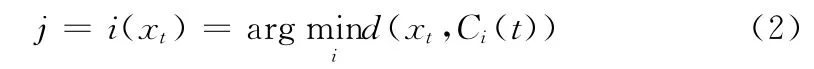
经过多次迭代后，xt距它所属于的输出节点最近，这样就能将时间序列xt进行量化。

1.3 DBSCAN聚类算法

聚类方法是多维统计分析的有效方法的一种，它将数据中最相近的数据分为一类，不同子类的数据尽可能不相似的方法。其中，DBSCAN算法是基于密度的聚类方法，它依据数据的分布密度来生成簇，同时它具有抗噪声的能力，而且能处理任何形状和大小的簇［12］。因此，在电机的多维状态参数中利用可以DBSCAN聚类算法（Density－Based Spatial Clustering of Applications With Noise，DBSCAN）时，不仅可以处理数据中的微小噪声，同时也能发现电机的异常数据。但是，仅仅利用DBSCAN的方法来分析电机的异常情况，如果最小包含点数（minPts）太小容易误判；但是如果取值太大，对电机的异常判定往往在发生异常一段时间之后，造成异常判断的滞后性。噪声序列。

由于平时电机如果不发生一些意外情况，一般不会发生突发性的故障，如：操作错误、电压波动等。设备往往更多的是在日积月累的磨损下，发生的渐变式故障。当电机出现异常的时候，检测到的状态参量常常变化并不大，不容易被察觉。因此，对于电机中那些状态量没有超过规定阈值的异常，仅仅使用AR模型并不能检测出来。

1.2 自组织神经网络

自组织神经网络（Self－Organized Map，SOM）是一种由互相连接的神经元阵列组成的自组织、无监督的竞争式学习网络，由输入层和竞争层两部分构成［11］。在SOM神经网络结构中，竞争层中的各个神经元，以欧式距离作为竞争的对比条件，竞争与输入向量相距最短。其中距离最短的为最优神经元，它与邻域中的其它节点相互激励，调整输入层和竞争层的连接权值，使领域中的节点对输入都能产生近似的输出结果。因此SOM算法可以计算出输入层中数据间的相似程度，并把相似度比较大的数据就近分配。

将电机基于时间序列的单一状态参量xt作为输入节点，利用SOM的算法进行训练，得到序列C＝｛C1，C2，…，CN｝作为输出节点，xt属于输出节点Cj可表示为：

2 基于时间序列的电机状态参量的特征挖掘

时间序列的自回归模型的记忆性恰好和电机工作状态参量数据连续性的特性相吻合，因此正好可以用来拟合电机状态参量的曲线。由于自组织神经网络SOM无监督分类的特性，电机的单一状态参量数据序列利用训练好的SOM神经网络训练后，就变为时间轴上的离散点序列Ct＝｛C1，C2，…，CN｝。因此，电机状态参量在SOM训练后，其中每个神经元节点的临近节点相关性最强，与其他的节点相关性弱［13］，量化生成的序列Ct可以看成是一个神经元转移到另一个神经元，这样来挖掘电机单一状态参量的变化特征。之后，利用DBSCAN聚类算法来处理多维状态参量之间的关系。

2.1 电机状态参量序列的概率密度函数

电机状态参量经过SOM神经网络训练后，若序列中数据之间的关系用转移概率来表示，那么相关性越大则转移的概率越大，反之，相关性越小则转移的概率越小。这样，我们把转移概率用P来表示，那么AR（1）模型中神经元之间的一阶转移概率为P［ct＋1|ct］。令｛C1，C2，…，CN｝的值为｛1，2，…，N｝，由式（2）可知，在t时刻时，ct为CI的概率可以表示为：

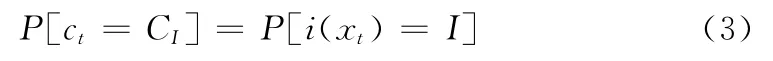
由式（3）可得i（xt）的概率密度函数为：

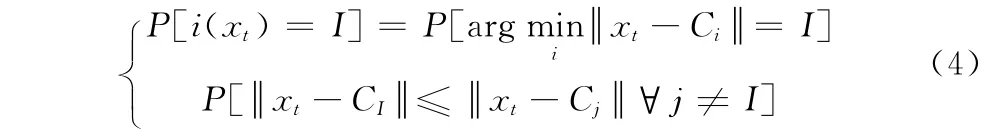
在式（1）中，et为正态分布序列，因此xt也应该为正态分布。令a＝（CI＋CI＋1）／2且b＝（CI＋CI－1）／2，则xt也应该为正态分布，xt的分布函数可以写为：

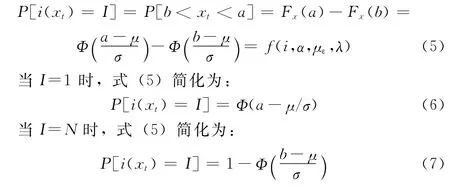
2.2 电机状态参量序列神经元之间的转移概率

因为AR模型中数据变化的低动态性，所以神经元之间的转移概率跟神经元之间距离成反比。神经元间转移概率分布函数为：

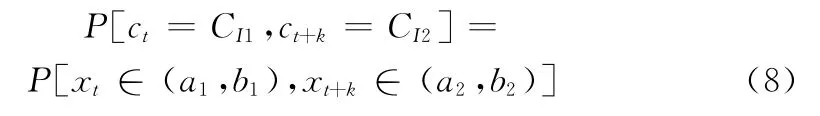
式中，CI1，CI2∈｛C1，…，CN｝，I1＝（a1，b1），I2＝（a2，b2），又xt为正态分布，则xt的分布函数为：

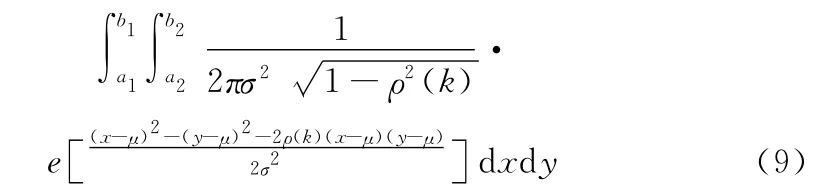
其中：ρ（k）＝αk表示AR（1）模型的自相关函数［14］。考虑神经元之间的渐变转移，由式（3）、（5）将式（9）变换为：

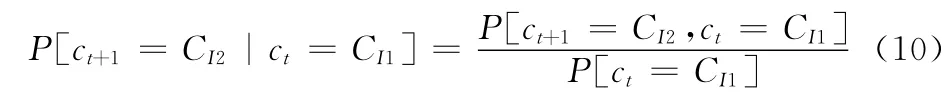
如果知道了神经元之间的转移概率，并将神经元之间的转移概率基于时间序列的顺序表示出来，这样我们就可以得到一个单状态量数据的转移概率序列。

现用电机的负荷数据来进行异常检测作为例子来说明该方法，首先把一组电机正常工作的温度数据带入AR（1）模型进行拟合，可以算得模型中参数α＝0.85，με＝0，λ＝0.01，然后将负荷数据输入到SOM中训练，得到该电机负荷的SOM模型。截取其中一段电机工作的负荷数据作为异常检测数据，如图1所示。利用得到的SOM模型进行量化后输出得到图2所示的电机负荷量化序列，利用拟合得到的AR模型的参数，计算SOM神经元间的转移概率，将负荷在时间轴上的序列转化成负荷在时间序列中的转移概率，如图3所示。

由图中的电机负荷转移概率序列可知，电机正常工作时，转移概率都比较高，这表明电机正常工作时温度数据变化不大，表明电机的工况比较稳定，电机工作正常。反之，当序列中的一段数据很小，甚至为零时，表明神经元随后的变化较大，可能是电机出现了异常，导致负荷数据的变化不再符合建立的AR模型。

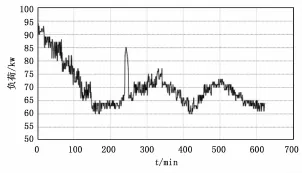
图1 电机负载数据图

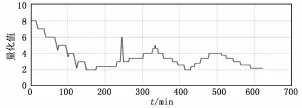
图2 电机负荷量化序列图

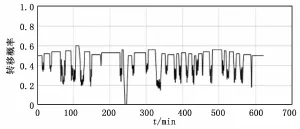
图3 负荷在时间序列中的转移概率

2.3 多维状态参量的综合判定

在实际情况中，电机运行出现异常时，虽然其中某个运行参数的变化量可能过小，但是更多伴随的是设备的多个运行参数的异常。如果只是针对单一检测状态量进行分析，可能导致对设备的异常出现误判，因此对多个状态量进行综合判定能有效的提高对异常判定的准确率。

同时，设备在实际运行时不仅在不同的工况下，设备的运行参数会产生差异，而且设备的多种参数之间的相关性和对异常的敏感性难以确切的表示出来。如电机的功率与震动、噪声、环境温度等参数的关系，难以通过简单的线性关系或者非线性关系算出［15］。这样，从多个状态参量出发的综合判定遇到了困难。

在无先验知识的情况下，聚类分析技术是解决上述问题的首选。针对多维参量融合的问题，利用电机工作出现异常时会产生离群点［16］，本文通过基于密度的聚类算法对多维历史检测数据进行聚类生成多个簇，然后去对需要监测的数据进行检测是否与历史数据属于同一类。若历史数据不属于生成的簇类，说明该时刻数据发生了异常。利用这种算法，不仅能解决不同状态参量对异常的敏感性不同和数据流过大的问题，还可以简化多种状态参量的相关性分析。

2.4 异常检测的方法

根据分析和挖掘设备多个状态参量的变化特征，并将多种状态参量结合判定异常的步骤如图4所示。

步骤1：针对设备正常运行的状态参量的历史监测数据，首先用AR模型来对数据进行拟合，然后用SOM算法来训练得到SOM网络模型，最后用拟合出来的AR模型，得到SOM神经元之间的转移概率矩阵。

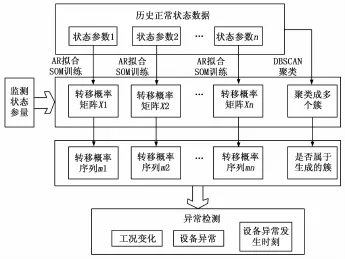
图4 设备异常检测流程图

步骤2：将设备的多维状态参量用DBSCAN算法聚类，得到多个簇类。

步骤3：将检测数据的状态参量带入转移概率矩阵，可以进行计算得到设备的多种状态参量的时刻概率转移序列。同时，判断每个时刻点是否属于之前生成的簇类。

步骤4：利用得到的转移概率序列和聚类的结果，对设备的异常判定方法为：

1）如果各种在线监测状态参量的数据都聚到了之前生成的簇类中，那么就可以判断该时间段没有出现异常。

2）如果各种在线监测状态参量的数据仅有少数几个时间点没有聚到了之前生成的簇类中，那么可以判断该时间段可能是数据异常或者传感器异常，并没有出现异常。

3）如果各种在线监测状态参量的数据出现一段时间段没有聚到了之前生成的簇类中，则可以判断电机已经处于异常。然后，再根据对应时刻之前的在线监测状态参量的转移概率序列来确定异常发生的点。

3 实验结果与分析

为了验证本文的算法，我以安庆石化港贮部的电机运行数据作为实验数据。该港贮部已实行了电能耗的智能化管理，通过传感器和监测仪器，可以将现场设备的运行参数采集并传送到监测室，然后对设备的运行数据进行监测和备份。本文利用2013年9月电机正常工作的状态参量数据作为历史数据，进行样本训练；然后，截取2013年10月中一天电机早上7点开机后连续工作的数据作为检测数据，电机温度、负荷、出口压力的采样周期都是min／组，如图5所示。

首先用AR模型来对选择的样本数据进行拟合，用SOM算法来训练得到SOM网络模型，然后用拟合出来的AR模型，得到电机温度、负荷、出口压力的转移概率矩阵，最后将图5所示的检测数据带入转移概率矩阵，分别得到负荷、电机温度、出口压力的转移概率序列，并进行聚类，结果如图6、7、8、9所示。

从上图中可以进行对截取的检验样本数据进行判断：

1）在时间t＝85（对应时间8：25）和t＝350（对应时间12：50）左右时，电机温度、负荷、出口压力的聚类结果出现0值，这说明该时刻电机的状态参量不属于得到的任何一个簇类，但是该0值只是在几个时刻短暂的出现，判断该时间段可能是数据异常或者传感器异常，并没有出现异常。

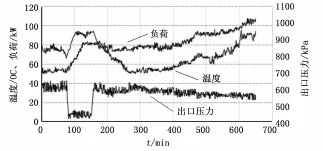
图5 电机的检测数据图

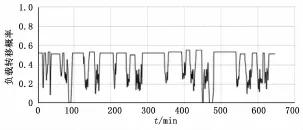
图6 负荷转移概率图

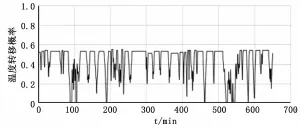
图7 温度转移概率图

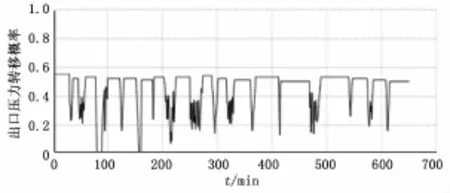
图8 出口压力转移概率图

2）在时间t＝580（对应时间16：40）左右时，电机出现一段时间的0值，之后出现短暂的1值后保持0值，这说明电机已经处于异常状态。然后查看状态量序列，其中电机负载转移概率在t＝460和电机温度转移概率在t＝470分别出现了0值，之后又多次出现0值，因此可以判断电机在t＝460时发生了异常。

如直接采用阈值判断，根据经验通常选择正常工作数据的1.2倍。用该方法判断：在t＝110（对应时间8：50）和t＝480（对应时间14：00）之后出现异常。

如单独采用聚类方法判断，如采用DBSCAN聚类算法对电机进行检测时：在t＝90（对应时间8：30）、t＝350（对应时间8：30）和t＝570（对应时间8：30）之后出现离群点，判断在t＝90和t＝350时，可能为数据或者传感器的异常，在t＝570时刻出现异常。

如采用神经网络训练的方式，选用常用的BP神经网络进行训练得到结果：在t＝480（对应时间14：00）、和t＝520（对应时间14：40）之后多次出现异常。

查阅当天该电机的运行记录显示：在8：20时，操作员为了应客户时间要求，调大了泵的阀门开度，加大传输速度；在10：00时将开度调回至正常；在14：00时发现电机转轴出现轻微卡轴，整理可得表1。

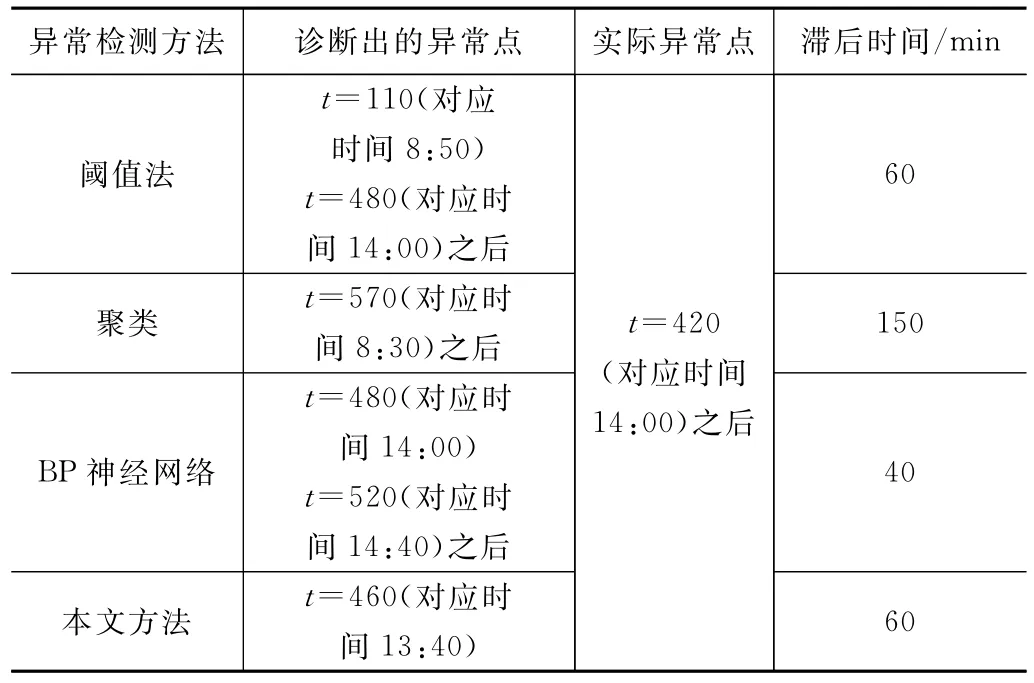
表1 异常检测结果对比

对比发现，该本文的方法对于电机的异常检测更准确、更及时。

之后，在安庆石化港贮部2014年－2015年的电机运行数据中截取100段，利用不同的方法来进行异常检测，其中误报率为检测结果中存在检测错误的百分比，滞后率以滞后400分钟为基准进行整理可得到表2。

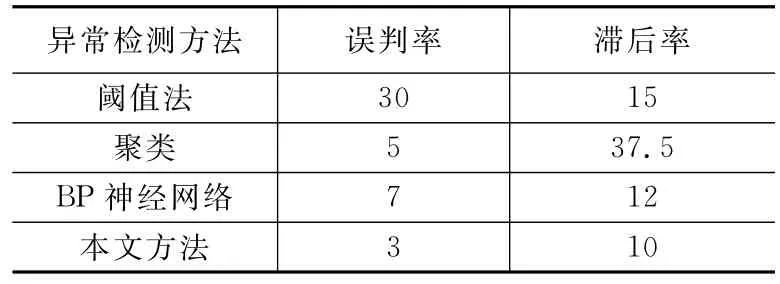
表2 不同方法异常检测结果对比 %_

该表表明，相比于阈值判断法、BP神经网络和单一的聚类的方法，本方法能对用电设备进行更加有效的异常检测，能减少误判和对异常发现的滞后性。

4 结论

该方法基于时间序列结合多维参数特征挖掘数据变化特征，利用聚类方法提高对电机异常检测的准确率，同时利用分析数据的变化特征来减少诊断结果的滞后性。

同时，本方法也有不足之处，当选取的多维参数特征受外界影响特别大时，DBSCAN聚类的算法聚类比较麻烦，因而容易出现对异常的误报，因此在今后的工作中需要进行改进。

［1］高贾超.基于人工免疫算法的电机故障诊断系统研究［D］.武汉：武汉理工大学，2010.

［2］盖诗桥.时间序列挖掘系统中变化检测算法的研究［D］.长春：吉林大学，2012.

［3］史尚哲.基于隐马尔科夫模型的异常检测［D］.扬州：扬州大学，2012.

［4］付迎丁.基于聚类技术的异常检测研究［D］.郑州：解放军信息工程大学，2012.

［5］龚学兵，王日新，徐敏强.基于数据关联性分析的飞轮异常检测［J］.航空学报，2015，36（3）：898－906.

［6］董晓萌，罗凤娟，郭满才，等.时间序列的自回归模型在杨凌地区降水量预报中的应用 ［J］.中国农学通报，2007，23（11）：403 －407.

［7］刘井波.基于自组织神经网络的远程故障诊断技术研究［D］.成都：电子科技大学，2008.

［8］闫庆华，程兆刚，段云龙.AR模型功率谱估计及Matlab实现［J］.计算机与数字工程，2010，38（4）：154－156.

［9］冯少荣，肖文俊.DBSCAN聚类算法的研究与改进［J］.中国矿业大学学报，2008，37（1）：105－111.

［10］高 洁.基于时间序列理论方法的生物序列特征分析［D］.无锡：江南大学，2009.

［11］于鷃.基于一维SOM神经网络的聚类及数据分析方法研究［D］.天津：天津大学，2009.

［12］宋飞燕.基于密度聚类算法及其模式评估方法的研究与实现［D］.包头：内蒙古科技大学，2007.

［13］严英杰，盛戈皞，陈玉峰，等.基于大数据分析的输变电设备状态数据异常检测方法［J］.中国电机工程学报，2015，35（1）：52 －59.

［14］程 浩，刘国庆，成孝刚.一种分段平稳随机过程自相关函数逼近模型［J］.计算机应用，2012，32（02）：589－591.

［15］Shumway－Cook A，Woollacott MH.Motor control：theory and practical applications［M］.Williams＆ Wilkins.

［16］李 栋，刘树林，刘颖慧，等.基于自适应超环检测器的设备异常度检测方法［J］.机械工程学报，2014，50（12）：17－24.

Anomaly Detection of Electric Machine Based on Multi－dimension State Parameter and Time Series

Xu Shoukun ，Qu Shiqi，Shi Lin，Wang Bin

（College of Information Science and Engineering，Changzhou University，Changzhou 213000，China）

In view of the traditional abnormal detection of the motor often appear the case of miscarriage of justice or lag，this paper using AR fitting and SOM neural network unsupervised way to quantify the motor data based on the time series of the motor single state parameters.Then，the transition probability of the sequence is obtained by combining the quantitative sequence with the AR curve，and the abnormal changes of some state parameters are discovered as soon as possible.After that，DBSCAN algorithm mining multi－dimensional parameters of the relationship between the characteristics of the motor to determine whether there is abnormal.Finally，the detection process of the method is illustrated with an example，and the advantages of this method are verified by comparison.

anomaly detection；time series；AR fitting；SOM neural network；DBSCAN algorithm

1671-4598（2016）08-0032-04

10.16526／j.cnki.11－4762／tp.2016.08.009

：TP391

：A

2016-02-24；

：2016-03-08。

江苏省产学研联合创新基金（BY2013024－06）；江苏省产学研联合创新基金（BY2013024－03）。

徐守坤（1972-），男，山东省人，教授，硕士研究生导师，主要从事数据库和信息系统方向的研究。