大截面导线间隔棒最大次档距分析

张 瑚，李雨蔓，李 健，周 魁，张冯硕

(1.中国电力工程顾问集团中南电力设计院有限公司，湖北 武汉 430071；2.重庆大学电气工程学院，重庆 400044)

大截面导线间隔棒最大次档距分析

张 瑚1，李雨蔓2，李 健1，周 魁1，张冯硕1

(1.中国电力工程顾问集团中南电力设计院有限公司，湖北 武汉 430071；2.重庆大学电气工程学院，重庆 400044)

论述次档距振荡对输电线路的危害和国内外常规的处理措施，对分裂导线最大次档距取值的主要遵循的有关理论进行阐述，主要为抗扭转和抑制次档距振荡。对±800 kV特高压线路6×JL/G2A－1250/100大截面导线的次档距振荡特性进行算例分析，从覆冰和不覆冰两种情况下的次档距振幅进行计算，得出不同覆冰下满足条件的最大次档距取值，同时对导线扭转恢复特性进行计算分析，得出扭转恢复要求的次档距不起控制作用。推荐±800 kV特高压线路大截面导线间隔棒最大次档距推荐取值。

±800 kV；特高压；大截面导线；次档距振荡；间隔棒布置。

1 概述

目前，我国高压输电线路多采用分裂导线，主要是扩大导线束的等值外径，减少线路的电晕，提高线路的输送容量。但是，分裂导线在机械性能上却比单根导线更加复杂，学者们通过对一系列输电线路故障的研究分析，发现风力对分裂导线起控制作用。

风在架空输电线路导线上振动主要有三种形式：微风振动、次档距振荡和舞动。其中，次档距振荡是指分裂导线上两间隔棒之间的子导线振动，是采用相分裂导线的线路所特有的机械运动现象，极易发生。次档距振荡会造成各子导线的互撞和鞭击，使导线线股磨损，同时会导致间隔棒夹头处产生较大的动弯应力，从而使间隔棒松动甚至损坏，严重时可造成导线断股、短路等事故。我国次档距振荡比较的严重的区域主要发生在西北大风地区，在2008年，甘肃和宁夏相继发生了导线次档距振荡事故，严重威胁输电线路的运行安全。

在分裂导线中，对间隔棒进行合理布置是控制次档距振荡的重要措施，而进行间隔棒布置的首要问题就是确定间隔棒的最大次档距对于最大次档距，一般设计中都是依据经验进行。

根据抑制次档距振荡的经验，加拿大建议最大次档距不超过68 m；根据子导线摇摆碰撞认为， 德国500 kV以下线路的次档距限制在初40～50 m，而美国最大次档距可放至76 m；加拿大Ander 公司规定的两级最大次档距：开阔地带取68 m， 非开阔地带取76 m；这些数据均有各自的试验依据，但分散性太大，不易把握，且缺少理论依据。

随着大截面导线在±800 kV特高压直流输电线路上的应用，如何采取有效防振措施防止导线的次档距振荡研究显得很有必要。

2 最大次档距取值的相关理论

间隔棒的主要作用是支撑子导线，防止子导线相互碰撞和鞭击，抑制次档距振荡。对于间隔棒的安装距离及数量，除了考虑经济因素外，还必须从防止导线碰撞和翻转，能达到最佳防振效果进行必要的研究和计算，主要考虑的因素有：

(1)对于平均风阻力和正常电流产生的电磁吸引力，间隔棒的安装距离必须使子导线不接触。

(2)对于尾流引起的次档距振荡，保证子导线不发生频繁的鞭击和金具的疲劳破坏。

(3)对于风和覆冰引起的扭转，允许子导线接触，但当覆冰和风等外力消失后，间隔棒的安装距离必须能使扭转自然恢复(称扭转复原理论)。

2.1 抗吸附条件下的次档距要求

由于风吸引力和电磁吸引力的作用，子导线会接近，当电流增大到某值时，子导线会突然吸附而不能脱离，因此，须限制间隔棒的安装距离，把子导线的接近率控制在一定的值。

对于输送大容量电流的输电线路，由于电磁力的作用，子导线相互吸附，如果风速加大，吸附将更容易。

因此有必要设定一个合适的间隔棒间隔距离，使得即使子导线吸附碰在一起，只要当外力消除，就可以自然地脱离开。

对于特高压输电线路而言，根据国外的研究，风压和电磁吸引力相对次档距振荡对间隔棒安装间距的影响而言要小得多。

2.2 次档距导线振荡特性

次档距档中子导线的振幅一般要求小于二分之一倍的子导线分裂间距，以避免子导线振荡时发生碰撞。在尾流区的子导线，次档距振荡的输入能量和衰减能量达到平衡时，就成为稳定振荡，由尾流中子导线的作用外力，可以推出间隔棒间距与次档距振幅之间近似计算公式：

式中：X0'为次档距振动幅值(m)；lc为最大次档距(m)；T为导线张力(N)；W为导线重量(kg/m)；a为子导线间距(m)；D为子导线外径(m)；E为振动幅值衰减率(0.05～0.1)，计算是一般取0.08。

2.3 扭转恢复要求的次档距要求

分裂导线不均匀覆冰时会产生较大的扭转力矩，加上风压会使导线发生严重的扭转。由于风压和覆冰产生扭转力的机理非常复杂，且覆冰厚度、形状具有不规则、不确定性，因此确定它的大小和设计条件是极其困难的问题。扭转设计中一般是按导线覆冰时发生的扭转，在脱冰后能自然恢复来考虑的。导线一旦发生扭转，为了使它自然复原，在任意扭转角下，经常有复原力在作用是必要的。为此，不论扭转角的大小，导线重力、导线张力、导线扭转刚度三种力引起的力矩总和，应使其为正值。导线的扭转恢复特性曲线计算主要步骤为：

(1) f1(λ)函数计算

先求等值线路常数M－，然后按照下式计算f1(λ)函数：式中：λ=S1/S；S1为为间隔棒距悬垂点的距离(m)；

S为为档距(m)；M－为为线路机械常数。

(2)扭转系数

多分裂导线的扭转刚性常数的计算公式：

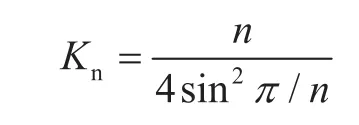
(3)扭转恢复特性曲线

结合前面算得的f1(λ)函数和扭转系数，可知：

式中：ηd为扭转恢复特性曲线的修正系数，一般取0.95；β为扭绞刚性常数；l为次档距(m)；

3 大截面导线算例分析

目前，我国特高压直流输电线路已采用六分裂1250 mm2截面导线，下面以6×JL/G2A－1250/100钢芯铝绞线为例，导线参数见表1。

表1 导地线参数

国内外相关研究表明，风压和电磁吸引力相对次档距振荡对间隔棒安装间距的影响较小，下面主要对大截面导线次档距振荡和扭转恢复特性进行研究，计算分析27 m/s风，10 mm、15 mm、20 mm冰区的次档距振荡规律。

3.1 导线次档距振荡计算

(1)完善相关的法律法规体系。法律是保障金融市场稳定的有力武器。我国资产证券化起步晚，与之相关的法律法规并不完善。拥有完备的法律体系会提高资产证券化发起人和投资人的安全感。同时，拥有完备的法律体系也会涉及其他领域的利益关系，对于经济发展十分有利。

结合国内外其他学者的研究成果及运行经验，取次档距大于40 m，核算次档距振幅。次档距振幅一般要求小于二分之一倍的子导线间距，以免子导线振荡时发生碰撞。对大截面导线特高压直流输电线路，进行不考虑覆冰和考虑覆冰两种工况的次档距振幅核算。

(1)不考虑覆冰

不考虑覆冰时有：子导线外径D=47.85 mm，子导线间距a=500 mm，风速V=16 m/s，导线张力T=7996 kg，导线重量W=4.25 kg/m。计算结果见表2。

表2 不考虑覆冰次档距振幅计算结果

(2)考虑覆冰

当导线覆冰时，子导线的振动幅值将增大，间隔棒上所承受的荷载也将增大。按照设计覆冰分别为10 mm、15 mm、20 mm，计算大截面导线在不同覆冰下的次振荡特性，计算结果见表3、表4、表5。

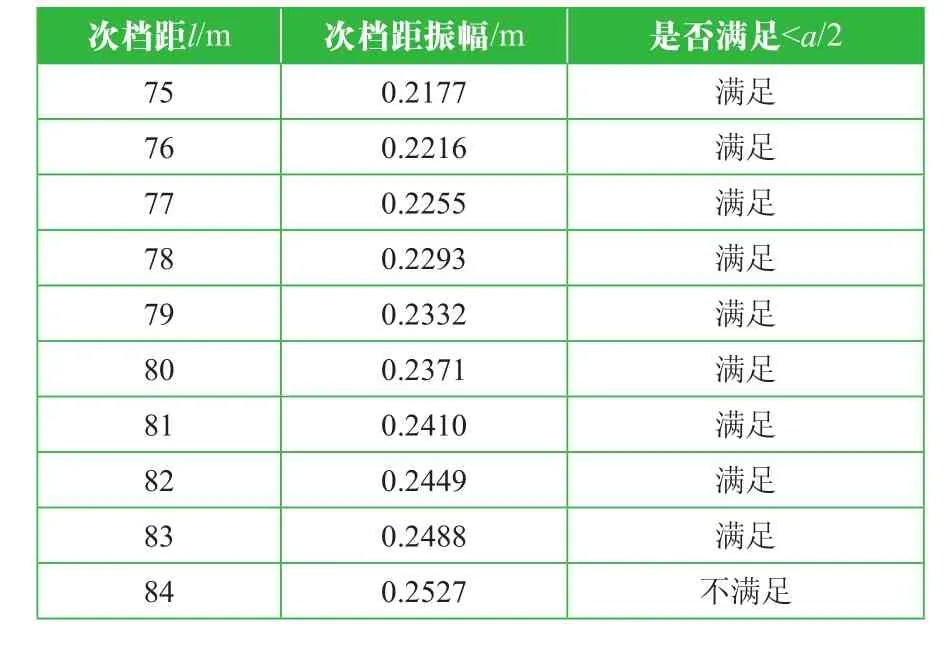
表3 考虑覆冰厚10 mm次档距振幅计算结果

表4 考虑覆冰厚15 mm次档距振幅计算结果

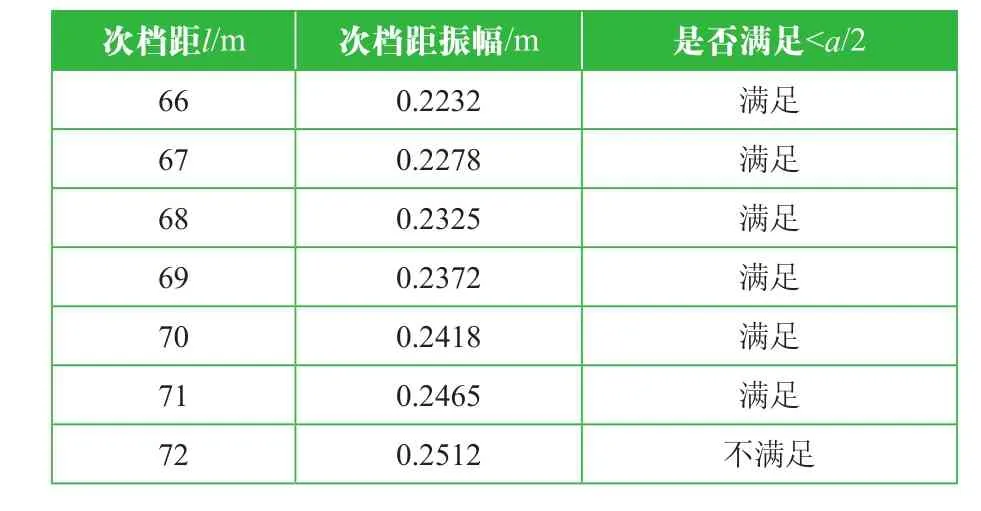
表5 考虑覆冰厚20 mm次档距振幅计算结果

从表2计算结果可知，导线无冰时允许的次档距比较大，满足子导线振动幅值要求的最大次档距达100 m。

从表3、表4、表5可知，10 mm、15 mm、20 mm覆冰时满足子导线振动幅值要求的最大次档距分别为83 m、77 m、71 m。

3.2 导线扭转恢复特性

6×JL/G3A-1250/100钢芯铝绞线呈正六边形排列，分裂间距a=500 mm，导线平均运行张力T=78.44 kN，导线重量W=4.25 kg/m，导线外径D=47.85 mm，进行经济档距510 m下的扭转恢复特性曲线计算。

根据式(2)～(4)，即可得到六分裂导线耐张档的扭转恢复特性曲线函数：

分析本工程六分裂导线的扭转恢复特性曲线，可以看出档距中部间隔棒最大次档距可取到115 m，可满足自然恢复要求。

结合扭转恢复特性曲线的计算过程，一般情况下，抗扭恢复力对档距中部间隔棒最大间距不起控制作用。

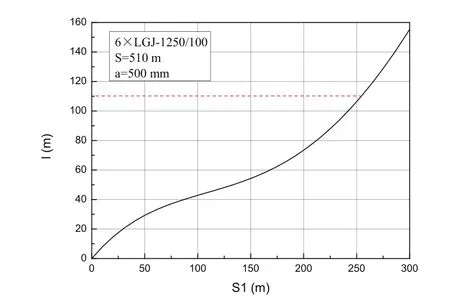
图1 导线扭转恢复特性曲线

3.3 间隔棒最大次档距取值

结合图1导线扭转恢复特性曲线可知，6×JL/G2A－1250/100大截面在档距510 m时，导线档距中部间隔棒最大次档距可取到115 m，可满足自然恢复要求，抗扭恢复力对档距中部间隔棒最大间距不起控制作用。

结合表2、表3、表4计算结果，大截面导线最大次档距主要受覆冰下的次档距振荡影响，10 mm、15 mm、20 mm覆冰时理论条件下最大次档距分别为83 m、77 m、71 m。

在实际工程中，结合运行经验，综合考虑各种因素，6×JL/G2A-1250/100大截面导线输电线路10 mm和15 mm冰区，一般地区档距小于1000 m时，最大次档距取66 m；档距大于1000 m时，最大次档距取60 m。20 mm冰区，最大次档距取55 m。

4 总结

综合以上对六分裂大截面导线次档距的研究，可以得出以下结论：

(1)特高压直流输电线路由于分裂根数多，导线截面大，间隔棒最大次档距应按照满足抗吸附、抗扭转和抑制次档距振荡三方面要求进行具体分析计算，以区别于以往的经验取值。

(2)对于直流特高压6×JL/G3A-1250/100导线而言，扭转恢复要求的次档距不作为控制条件，间隔棒最大次档距主要由覆冰时次档距振荡幅值控制。

(3)在本文特定计算条件下，六分裂导线6×JL/G2A-1250/100，年平张力取25%的计算拉断力时，不同覆冰区下导线间隔棒最大次档距理论算值和工程实际取值见表6。

Analysis on the Maximum Subspan for Spacing Stick in Large Cross-section Conductors

ZHANG Hu1, LI Yu-man2, LI Jian1, ZHOU Kui1, ZHANG Feng-shuo1
(1.Central Southern China Electric Power Design Institute Co.Ltd. Of China Power Engineering Consulting Group, Wuhan 430071, China；2.School of Electrical Engineering,Chongqing University, Chongqing 400044, China )

In this paper,it introduce the characteristic of Subspan Oscillation and the theory of how to choose the maximum Subspan of Spacers.The maximum Subspan is calculate with considerding anti-adsorption conditions,the amplitude limitations of sub-conductors and requirements of the reverse recovery characteristics.Then,a example is given on the analysis characteristic of Subspan Oscillation on ±800 kV UHV Transmission Line with 6×JL/G2A-1250/100 Conductors. It calculate the vibration amplitude of sub-conductors with or without ice and the reverse recovery characteristics to determine the maximum Subspan between Spacers. At last,the paper recommend the maximum Subspan between Spacers for ±800 V UHV Transmission Line with 6×JL/G2A-1250/100 Conductors in diffent design ice.

±800 kV; UHV; large cross-section conductors; subspan oscillation; spacer configuration.

TM75

B

1671-9913(2016)06-0065-04

2015-11-18

张瑚(1984- )，男，湖北黄陂人，硕士，高级工程师，从事高压输电线路的设计研究工作。