基于滑脱、应力敏感和非达西效应的页岩气压裂水平井产能模型
2017-01-13申智强潘少杰董力珲
田 冷, 申智强, 王 猛, 潘少杰, 肖 聪, 董力珲
( 1. 中国石油大学(北京) 石油工程教育部重点实验室,北京 102249; 2. 中国石油大学(北京) 石油工程学院,北京 102249 )
基于滑脱、应力敏感和非达西效应的页岩气压裂水平井产能模型
田 冷1,2, 申智强1,2, 王 猛1,2, 潘少杰1,2, 肖 聪1,2, 董力珲1,2
( 1. 中国石油大学(北京) 石油工程教育部重点实验室,北京 102249; 2. 中国石油大学(北京) 石油工程学院,北京 102249 )
基于页岩气藏压裂水平井三线性流模型,考虑页岩气滑脱效应,分析页岩气的吸附、天然裂缝的应力敏感和人工裂缝的非达西效应,建立页岩气产能模型,运用全隐式有限差分和牛顿—拉普森迭代法进行数值求解,绘制无因次产量递减曲线。结果表明:页岩气的流动阶段分为人工裂缝中不稳定线性流阶段、人工裂缝和微裂缝的双线性流阶段、微裂缝中不稳定线性流阶段、微裂缝和基质的双线性流阶段、基质中线性流动阶段、边界流阶段;如果忽略滑脱效应,将导致页岩气产能预测产生误差。当页岩基质孔隙直径小于20 nm时,滑脱效应造成的产量增加5%~25%。该结果对于认识页岩气藏水平井产能递减规律具有指导意义。
页岩气; 水平井; 纳米孔隙; 滑脱效应; 应力敏感效应; 非达西渗流
0 引言
气体的滑脱效应是指气体在介质孔道中出现在孔壁处的气体分子,沿着孔壁方向作定向运动,在孔壁处的流速值不为零的现象。对于常规储层,岩石孔隙较大,天然气流动产生的滑脱效应很弱,可以忽略不计[1]。页岩储层[2-4]的孔隙是纳米级别,其滑脱效应较常规储层的明显,如果忽略滑脱效应,将对页岩气的产能预测造成较大的误差[5]。
页岩储层一般被简化为双重孔隙或三重孔隙模型。Barenblatt G I等提出页岩气双孔拟稳态流动模型[6];Warren J E[7]等对该模型加以完善,提出不稳定渗流模型,但未考虑页岩气解吸和扩散影响。Kucuk F等[8]基于Warren-Root双孔模型,建立页岩气藏非稳态解析模型,但是未考虑页岩气吸附特性,使用数值模拟方法证明吸附态页岩气的存在。Carlson E S等将页岩气解吸和扩散流动特性耦合于常规双孔介质模型,建立考虑吸附、解吸和扩散的页岩气藏渗流模型[9],但是将页岩气的垂直裂缝井简化为无限大半径的非压裂直井,求得的压力响应并不能反映垂直裂缝井的流动特征。Ozkan E等研究页岩基质中气体向天然裂缝网络的流动机理,考虑页岩气在基质中同时存在渗流和扩散作用的双重机制,建立双重机制双孔模型[10],分析页岩气在储层中的流动,但是忽略吸附气的存在。王海涛[11]等基于页岩气双孔球形流模型,考虑页岩气解吸、扩散和微裂缝的应力敏感效应影响,但是将人工裂缝视为无限导流裂缝,与实际页岩气藏压裂水平井流动方式不符。El-Banbi A H提出线性三孔模型[12],给出拉普拉斯空间解,但是未考虑页岩气解吸和扩散影响。Alahmadi H A基于水平井的三孔线性流模型,建立考虑页岩气的吸附、解吸及扩散影响的新模型[13],但是未考虑微裂缝的应力敏感效应。田冷等[14]在文献[13]模型的基础上,考虑微裂缝的应力敏感效应和近井筒的高速非达西效应,但是假设页岩气在基质中的流动为分子扩散,并未考虑页岩气的滑脱效应。郭小哲[15]等考虑页岩气滑脱效应和吸附、解吸的影响,建立页岩气的产能模型,但是未考虑微裂缝的应力敏感效应和人工裂缝的非达西效应。
基于页岩纳米孔隙的滑脱流动,笔者考虑页岩气的吸附、天然裂缝的应力敏感和人工裂缝的非达西效应,建立页岩气产能模型,应用全隐式有限差分和牛顿—拉普森迭代法进行数值求解,并绘制页岩气产能递减曲线。
1 产能模型
假设条件:(1)矩形封闭地层中心一口水平井定压生产[16],初始地层压力为pi;(2)页岩储层为三重介质,分别为基质、微裂缝和人工裂缝;(3)气体的流动为三线性流,即气体先从基质向天然裂缝进行线性流动,然后由天然裂缝向人工裂缝进行线性流动,最后通过人工裂缝向井筒供气;(4)基质的流动为滑脱流动,考虑气体的滑脱效应;(5)人工裂缝具有有限导流能力[17],考虑人工裂缝非达西流动和天然裂缝应力敏感效应;(6)所有的介质为均质且各向同性;(7)页岩气解吸满足Langmuir等温吸附方程;(8)不考虑重力和毛细管力的影响。
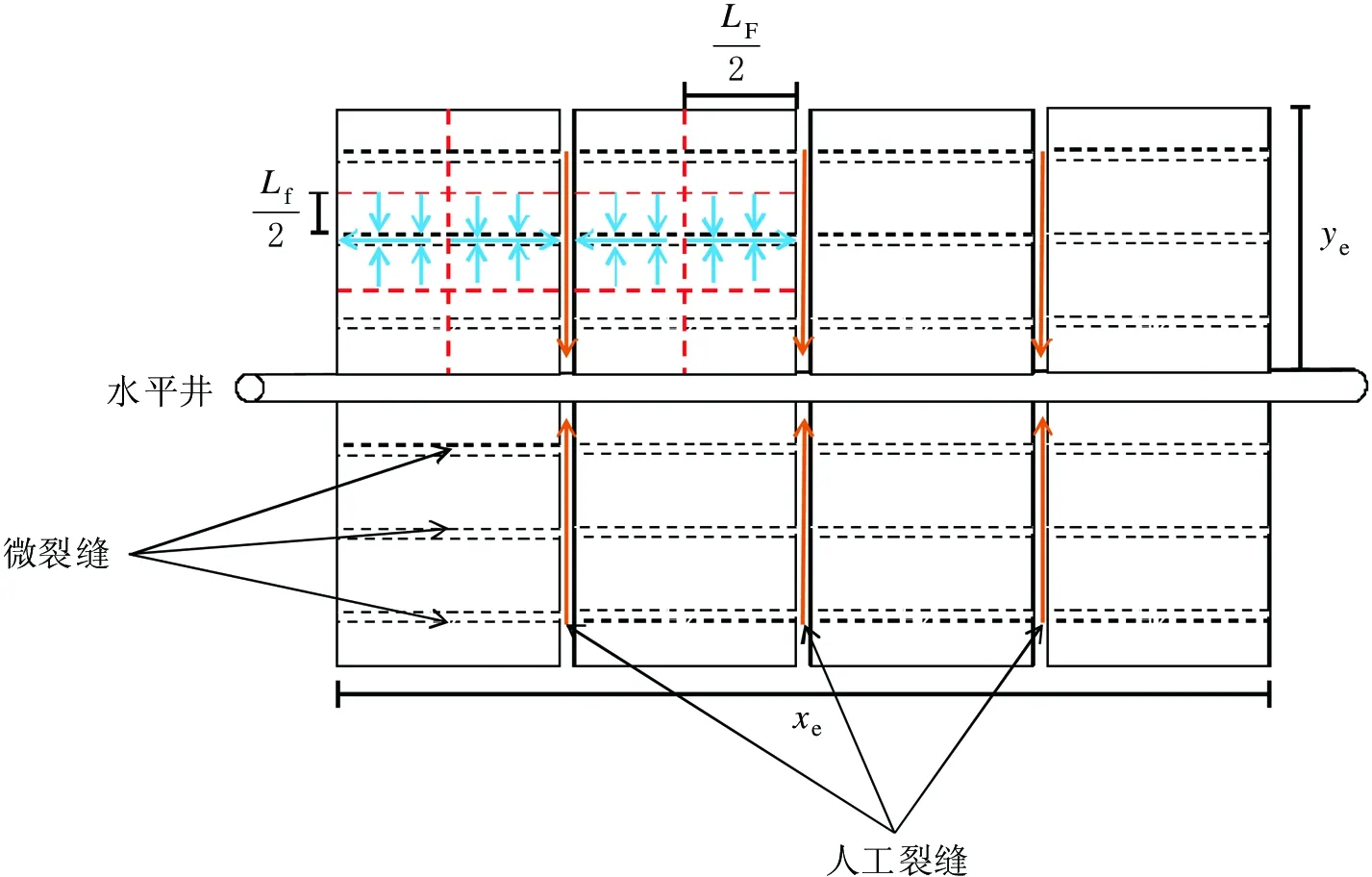
图1 水平井多级压裂三线性渗流的理论模型
1.1 滑脱效应
页岩基质孔隙为纳米孔隙,横截面小,从而产生气体滑脱效应。判断气体在不同尺度的流动通道内的流动是否存在滑脱效应,是由克努森数决定的。克努森数Kn为气体的平均自由程λ与孔隙直径d之比[5]:
(1)
(2)
式中:kB为玻尔兹曼常数,kB=1.380 5×10-23J/K;T为温度;δ为碰撞分子直径;p为压力。
当Kn≤1×10-3时,气体在微孔隙中的流动为黏性流,即达西流动;当1×10-3
假定某一页岩气藏温度为353 K,利用式(1-2)计算不同压力条件下、CH4在不同孔隙中流动时的克努森数,判断不同流态的界限,如孔隙直径为10~100 nm的页岩储层,在20~50 MPa压力内属于滑脱流动[5]。
通常用Klinkenberg方程描述气体的滑脱效应,Klinkenberg L J引入表观渗透率修正滑脱效应的影响[18]:
(3)
式中:Kb为气体表观渗透率;K∞为等效液体渗透率;c≈1。
引入滑脱效应修正系数τ,令
(4)
一般将滑脱效应修正系数τ作为常数,但是τ为关于压力的函数,得到气体渗流速度与滑脱效应的关系:
(5)
式中:υ为气体渗流速度;μ为气体黏度。
1.2 应力敏感效应
应力敏感效应的拟压力表达式[19-20]为
(6)
式中:K为考虑应力敏感的地层渗透率;Ki为原始地层渗透率;β为应力敏感系数;Ψi为原始地层拟压力;Ψ为地层拟压力。
1.3 非达西效应
非线性渗流二项式表征为
(7)

引入非达西流动效应修正系数ζ,则式(7)可以简化为
(8)
(9)
1.4 吸附效应
采用Langmuir等温吸附方程描述页岩气的吸附、解吸过程[21-22]:
(10)
对式(10)进行拟压力处理,有
(11)
式中:VE为平衡吸附浓度;pL为兰格缪尔压力;VL为兰格缪尔吸附体积;ΨL为兰格缪尔拟压力。
1.5 数学模型
从岩石表面解析出来时,页岩气由基质向天然裂缝及天然裂缝向人工裂缝的窜流为不稳定窜流,由连续性方程可以分别推导基质、天然裂缝和人工裂缝的渗流微分方程。
1.5.1 渗流方程
(1)基质

(12)
其中:
(13)
(2)天然裂缝
(14)
(3)人工裂缝
(15)
式(13-15)中:Ψm、Ψf、ΨF分别为基质、天然裂缝和人工裂缝的拟压力;φm、φf、φF分别为基质、天然裂缝和人工裂缝的孔隙度;μm、μf、μF分别为基质、天然裂缝和人工裂缝的黏度;Ctm、Ctf、CtF分别为基质、天然裂缝和人工裂缝的综合压缩系;Kmi、Kfi、KF分别为基质、天然裂缝和人工裂缝的渗透率;t为时间;psc为地面标准状况下的压力;Tsc为地面标准状况下的温度;x、y、z为距离,其中z方向平行于y;Lf为天然裂缝之间的距离;LF为人工裂缝之间的距离。
1.5.2 无因次量
(1)压力
(16)
(2)时间
(17)
(3)储容比
(18)
(4)裂缝导流能力比
(19)
(5)窜流系数
(20)
(6)应力敏感系数
βD=β(Ψi-Ψwf);
(21)
(7)初始拟压力
(22)
(8)兰格缪尔拟压力
(23)
(9)兰格缪尔体积
(24)
(10)产量
(25)
(11)距离
(26)
式(16-26)中:Acw为井筒泄流面积,Acw=2Lh,L为井筒长度,h为地层厚度;qsc为地面标准状况下的气体流量;Ψwf为井底拟压力。
1.5.3 综合方程
(1)基质
(27)
初始条件:ΨDm(zD,0)=0。
内边界条件:zD=1,ΨDm=ΨDf。
(2)天然裂缝
(28)
初始条件:ΨDf(xD,0)=0。
内边界条件:xD=1,ΨDm=ΨDf。
(3)人工裂缝
(29)
初始条件:ΨDF(yD,0)=0。
内边界条件:ΨDF(0,tD)=1。
2 产能模型求解
式(27-29)是关于拟压力的强非线性偏微分方程,采用数值方法求解。首先利用全隐式有限差分法将方程离散,然后采用牛顿—拉普森迭代法进行数值求解。
2.1 基质
(30)
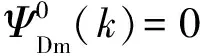
2.2 天然裂缝
(31)

2.3 人工裂缝
(32)

式(30-32)中:i、j、k分别为x、y、z方向上的网格标号。
3 产能递减曲线
某页岩气藏基本参数见表1,应用牛顿—拉普森迭代法数值求解产量模型,绘制产量递减曲线(见图2)。

图2 某页岩气藏无因次产量、时间的双对数典型曲线及流动阶段划分
根据某页岩气藏无因次产量和时间的双对数典型曲线的斜率,可以将页岩气的流动过程划分为6个阶段:
Ⅰ.人工裂缝中不稳定线性流阶段,持续时间较短,双对数曲线斜率为-1/2;
Ⅱ.人工裂缝和微裂缝中双线性流阶段,双对数曲线斜率为-1/4;
Ⅲ.微裂缝中不稳定线性流阶段,持续时间较短,双对数曲线斜率为-1/2;
Ⅳ.微裂缝和基质中双线性流阶段,双对数曲线斜率为-1/4;
Ⅴ.基质中线性流动阶段,持续时间最长,是最主要的流动阶段;
Ⅵ.边界流阶段,压力传导至边界,产量急剧下降。
某页岩气藏考虑滑脱效应和不考虑滑脱效应时无因次产量递减曲线见图3。由图3可知,考虑滑脱效应时,整体曲线上移。在纳米孔道中流动时,页岩气分子孔壁处的气体分子沿着孔壁方向作定向运动,孔壁处的流速值并不为零,在宏观上体现为气流量更大。
某页岩气藏不同孔隙直径时滑脱效应对无因次产量的影响见图4。由图4可知,页岩基质的孔隙直径越小,曲线越往上移。因为孔隙直径越小,滑脱效应越显著,基质的表观渗透率也越大。

图3 考虑滑脱效应时无因次产量递减曲线Fig.3 Typical curves of considering the influence of slippage effect

图4 不同孔隙直径时滑脱效应对无因次产量的影响
Fig.4 Typical curves of different pore diameters the influence of slippage effect
某页岩气藏不同孔隙直径时滑脱效应对气井产量的影响见图5。由图5可知,当页岩基质孔隙直径小于20 nm时,滑脱效应导致的产量增加5%~25%。当孔隙直径小到一定程度时,页岩气在孔隙中的流态发生改变,滑脱流动的规律将不再适用。

图5 不同孔隙直径时滑脱效应对气井产量的影响
4 结论
(1)基于页岩纳米孔隙的滑脱流动,考虑页岩气的吸附、天然裂缝的应力敏感和人工裂缝的非达西效应,建立页岩气产能模型,用数值方法绘制无因次产量递减的典型曲线。
(2)页岩气的流动阶段分为6个阶段:人工裂缝中不稳定线性流阶段;人工裂缝和微裂缝中双线性流阶段;微裂缝中不稳定线性流阶段;微裂缝和基质中双线性流阶段;基质中线性流动阶段;边界流阶段。
(3)页岩基质孔隙为纳米级别,存在滑脱效应,如果忽略滑脱效应,将导致页岩气产能预测产生误差。当页岩基质孔隙直径小于20 nm时,滑脱效应造成的产量增加幅度为5%~25%。
[1] 高树生,于兴河,刘华勋.滑脱效应对页岩气井产能影响的分析[J].天然气工业,2011,31(4):55-58. Gao Shusheng, Yu Xinghe, Liu Huaxun. Impact of slippage effect on shale gas well productivity [J]. Natural Gas Industry, 2011,31(4):55-58.
[2] 杨镱婷,张金川,王香增,等.陆相页岩气的泥页岩评价——以延长下寺湾区上三叠统延长组长7段为例[J].东北石油大学学报,2012,36(4):10-17. Yang Yiting, Zhang Jinchuan, Wang Xiangzeng, et al. Source rock evaluation of continental shale gas: A case study of Chang7 of Mesozoic Yanchang formation in Xiasiwan area of Yanchang [J]. Journal of Northeast Petroleum University, 2012,36(4):10-17.
[3] 洪凯,汪志明,王小秋,等.页岩气储层压裂水平井产能模型[J].东北石油大学学报,2015,39(3):104-110. Hong Kai, Wang Zhiming, Wang Xiaoqiu, et al. Productivity model of the fractured horizontal wells in shale gas reservoirs [J]. Journal of Northeast Petroleum University, 2015,39(3):104-110.
[4] 任俊杰,郭平,王德龙,等.页岩气藏压裂水平井产能模型及影响因素[J].东北石油大学学报,2012,36(6):76-81. Ren Junjie, Guo Ping, Wang Delong, et al. Productivity model of fractured horizontal wells in shale gas reservoirs and analysis of influential factors [J]. Journal of Northeast Petroleum University, 2012,36(6):76-81.
[5] 葛洪魁,申颖浩,宋岩,等.页岩纳米孔隙气体流动的滑脱效应[J].天然气工业,2014,34(7):46-54. Ge Hongkui, Shen Yinghao, Song Yan, et al. Slippage effect of shale gas flow in nanoscale pores [J]. Natural Gas Industry, 2014,34(7):46-54.
[6] Barenblatt G I, Zheltov I P, Kochina I N. Basic concepts of the theory of seepage of homogeneous liquids in fissured rocks [J]. Journal of Applied Mathematical Mechanics, 1960,24(5):852-864.
[7] Warren J E, Root P J. The behavior of naturally fractured reservoirs [J]. SPE J, 1963(3):245-255.
[8] Kucuk F, Sawyer W K. Transient flow in naturally fractured reservoirs and its application to Devonian gas shales [C]//SPE Paper 9397 presented at the SPE Annual Technical Conference and Exhibition. Dallas: 1980.
[9] Carlson E S, Mercer J C. Devonian shale gas production: Mechanisms and simple models [J]. Journal of Petroleum Technology, 1991,43(4):476-482.
[10] Ozkan E, Raghavan R, Apaydin O G. Modeling of fluid transfer from shale matrix to fracture network [C]//SPE Paper 134830 presented at the SPE Annual Technical Conference and Exhibition. Florence: 2010.
[11] Wang H T. Performance of multiple fractured horizontal wells in shale gas reservoirs with consideration of multiple mechanisms [J/OL]. Journal of Hydrology, 2013,doi: http://dx.doi.org/10.1016/j.jhydrol.2013.12.019.
[12] El-Banbi A H. Analysis of light gas well performance [D]. Texas: Texas A&M University, 1998.
[13] Alahmadi H A. A triple-porosity model for fractured horizontal wells [D]. Texas: Texas A&M University, 2010.
[14] 田冷,肖冲,顾岱鸿.考虑应力敏感与非达西效应的页岩气产能模型[J].天然气工业,2014,34(12):70-75. Tian Leng, Xiao Cong, Gu Daihong. A shale gas reservoir productivity model considering stress sensitivity and non-Darcy flow [J]. Natural Gas Industry, 2014,34(12):70-75.
[15] 郭小哲,周长沙.基于滑脱的页岩气藏压裂水平井渗流模型及产能预测[J].石油钻采工艺,2015,37(3):61-65. Guo Xiaozhe, Zhou Changsha. Seepage model and productivity forecast based on slippage of fractureed horizontal wells in shale gas pool [J]. Oil Drilling & Production Technology, 2015,37(3):61-65.
[16] 李清泉,王新海,尹虎,等.页岩气藏数值模拟及井底压力动态分析[J].东北石油大学学报,2013,37(1):91-96. Li Qingquan, Wang Xinhai, Yin Hu, et al. Simulation of shale gas reservoirs and dynamic analysis of bottom hole pressure [J]. Journal of Northeast Petroleum University, 2013,37(1):91-96.
[17] 温庆志,李杨,胡蓝霄,等.页岩储层裂缝网络导流能力实验分析[J].东北石油大学学报,2013,37(6):55-62. Wen Qingzhi, Li Yang, Hu Lanxiao, et al. Experimental analysis of the flow conductivity of the network-like fractures in shale reservoirs [J]. Journal of Northeast Petroleum University, 2013,37(6):55-62.
[18] Heidement R A, Jeje A A, Mohtadi M F, et al. An introduction to the properties of fluids and solids [M]. Calgary, Alberta: University of Calgary Press, 1984:5-15.
[19] 邓佳,朱维耀,刘锦霞,等.考虑应力敏感性的页岩气产能预测模型[J].天然气地球科学,2013,24(3):456-460. Deng Jia, Zhu Weiyao, Liu Jinxia, et al. Productivity prediction model of shale gas considering stress sensitivity [J]. Natural Gas Geoscience, 2013,24(3):456-460.
[20] Pedrosa O A. Pressure transient response in stress-sensitive formations [C]// Paper SPE 15115 presented at the 1986 SPE California Regional Meeting. Oakland: Aprial, 1986:2-4.
[21] Bumb A C, McKee C R. Gas-well testing in the presence of desorption for coalbed methane and Devonian shale [J]. SPE Formation Evaluation, 1988,3(1):179-185.
[22] Lane H S, Watson A T, Lancaster D E. Identifying and estimating desorption from Devonian shale gas production data [C]//SPE Paper 19794 presented at the SPE Annual Technical Conference and Exhibition. San Antonio: Society of Petroleum Engineers, 1989.
2016-08-10;编辑:任志平
国家自然科学基金项目(U1562102);中国石油大学(北京)基金项目(2462015YQ0218)
田 冷(1977-),男,博士,副教授,主要从事油气井测试技术和气藏工程方面的研究。
TE328
A
2095-4107(2016)06-0106-08
DOI 10.3969/j.issn.2095-4107.2016.06.012
