一类伸缩因子为a的区间多小波的构造研究

张建基，王 刚，周小辉

（1.新疆师范大学 数学科学学院，新疆 乌鲁木齐 830054；2.浙江财经大学 东方学院 信息分院，浙江 嘉兴 314400）

一类伸缩因子为a的区间多小波的构造研究

张建基1，王 刚1，周小辉2*

（1.新疆师范大学 数学科学学院，新疆 乌鲁木齐 830054；2.浙江财经大学 东方学院 信息分院，浙江 嘉兴 314400）

区间多小波的研究是小波分析研究的热点问题，如何构造具有良好性质（紧支撑性、高消失矩等）的区间多小波是研究的焦点问题。文章给出了区间［0，1］上伸缩因子为a的区间多尺度函数和区间多小波的构造方法，并给出了构造算例。

区间多小波；伸缩因子；正交性

小波构造与性质的研究是小波理论的核心问题。除了Haar小波，不存在其他单小波能够同时具备紧支撑性，正交性，对称性等。为了弥补单小波的不足，人们提出了多小波理论如：GHM多小波，C-L多小波等。为了更好地研究多小波的构造与性质，V.Strela提出了两尺度相似变换（TST）。人们在此基础上做了大量的研究，并且做了进一步的推广［1-10］。众所周知，定义在实轴上的小波在许多领域中有很大的应用，然而，在很多实际问题中，如：图像、视频信号等，人们往往感兴趣于一个有限的区域，这时用直线上的小波处理会产生“边界效应”，导致处理效果不理想。这样，区间小波的研究引起人们的关注［11-12］。现在，区间多小波的研究更是研究的热点问题，如何构造具有良好性质（紧支撑性等）的区间多小波是研究的焦点。文章给出区间［0，1］上伸缩因子为a的区间多尺度函数和区间多小波的构造方法，并给出了构造算例。

1 预备知识

设L2(R)的一个伸缩为a多重多分辨分析是一个闭子空间序列，且满足下列条件：

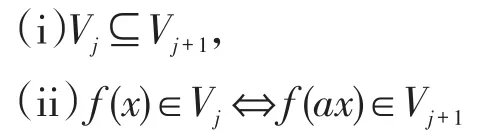
（iii）存在 向 量函 数Φ=[ϕ1,ϕ2,…ϕr]T∈L2(R)r使 得 集 合{Φ(x-k),k∈Z}是V0的 正 交 基 ，其 中。对于每一个j∈Z，定义Vj在Vj+1中的正交补空间Wj使得Vj+1=Vj⊕Wj，从 而 有⊕jWj=L2(R)。那么存 在 向 量 函数使 得是的正交基，其中。

其中r×r矩阵序列称为{} Pk称为两尺度矩阵序列；是对应的紧支撑正交多小波，并且满足下列两尺度方程：

在L2(R)情形下多小波基的构造基于Fourier技巧，即依赖于平移不变性。如果将函数限制于一个有限区间上，如［0，1］。那么在区间端点处建立一种非齐性，它破坏了平移不变性，因此为了构造L2[0,1]上的多小波基组，多重多分辨分析需要重新定义。设r≥2,γ>0是正整数，j0是满足如下条件的最小正整数j0=min{j:aj≥γ}，Kj=aj-γ。

令Φj,k(x)=aj 2Φ(ajx-k),j∈Z+,k∈Z。

定义1 设L2[0,1]的一个伸缩为a多重多分辨分析是一个闭子空间序列，，且满足下列条件：

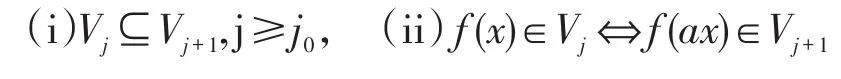
由于L2(R)上的区间多分辨分析已经有成熟的结果可供借鉴。因此可以通过L2(R)上的多小波（多尺度）函数进行某种截断来构造L2[0,1]上的a尺度的多小波。

2 伸缩为a的L2[0,1]上多尺度函数的构造

设Φ(x)是L2(R)r上支集为的伸缩为a的r重多尺度函数，它生成L2(R)r上的r重多分辨分析，Ψ1(x),Ψ2(x),…Ψa-1(x)是对应的多小波。这里的［·］表示取整函数。

定理1定义左边界多尺度函数)和右边界多尺度函数如下：

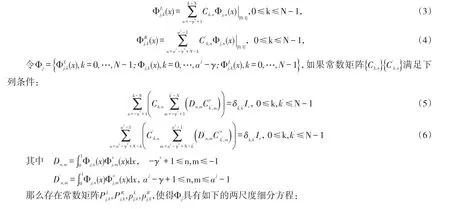
且在j≥logaγ上，Φj是空间Vj[0,1]上的一组规范正交基。

证明由

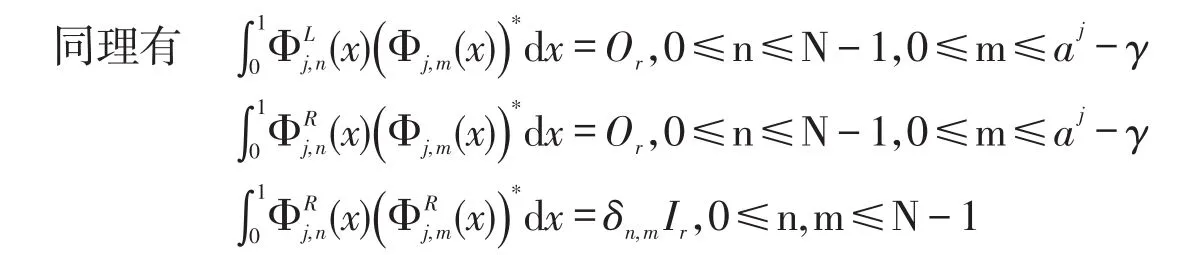
说明Φj是规范正交的。

下面证明Φj是空间Vj[0,1]上的一组基。

∀f∈Vj[0,1]，则f∈Vj(R)，则存在常数向量Aj,k，使得。

设f(x)可以写成如下形式：

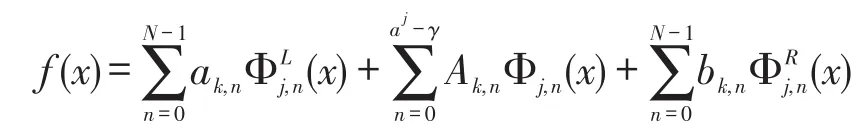
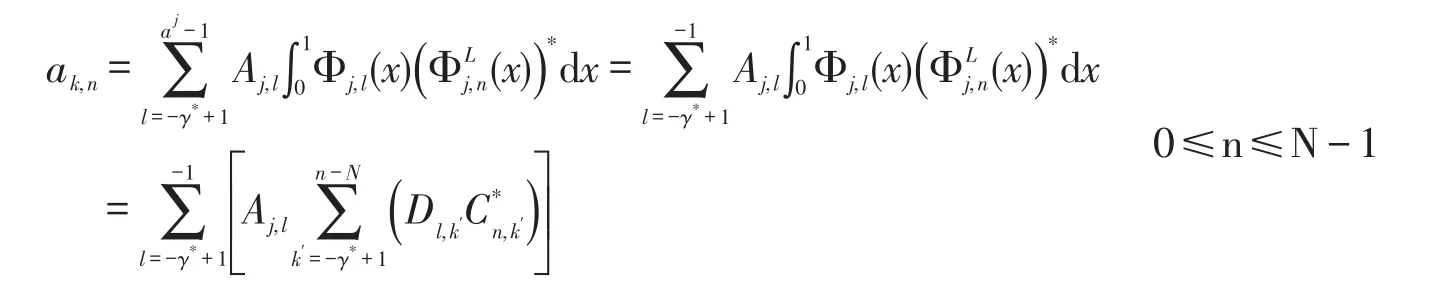
下面推导两尺度方程，

如果设当l<0,l>γ时Pl=O，又当n≤-γ*时对x∈[0,1]已经超出了支集。

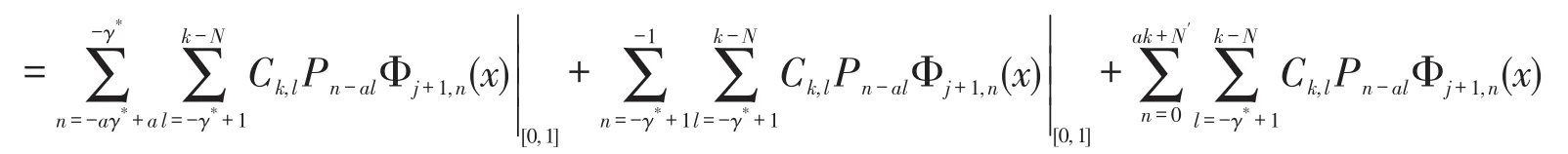
其中Ck,-γ*+1,…,Ck,-1满足约束条件（11）。

若PLj,k满足条件（10），（11）和（12），那么就有两尺度方程：

同理可得右边界多尺度函数的两尺度方程：

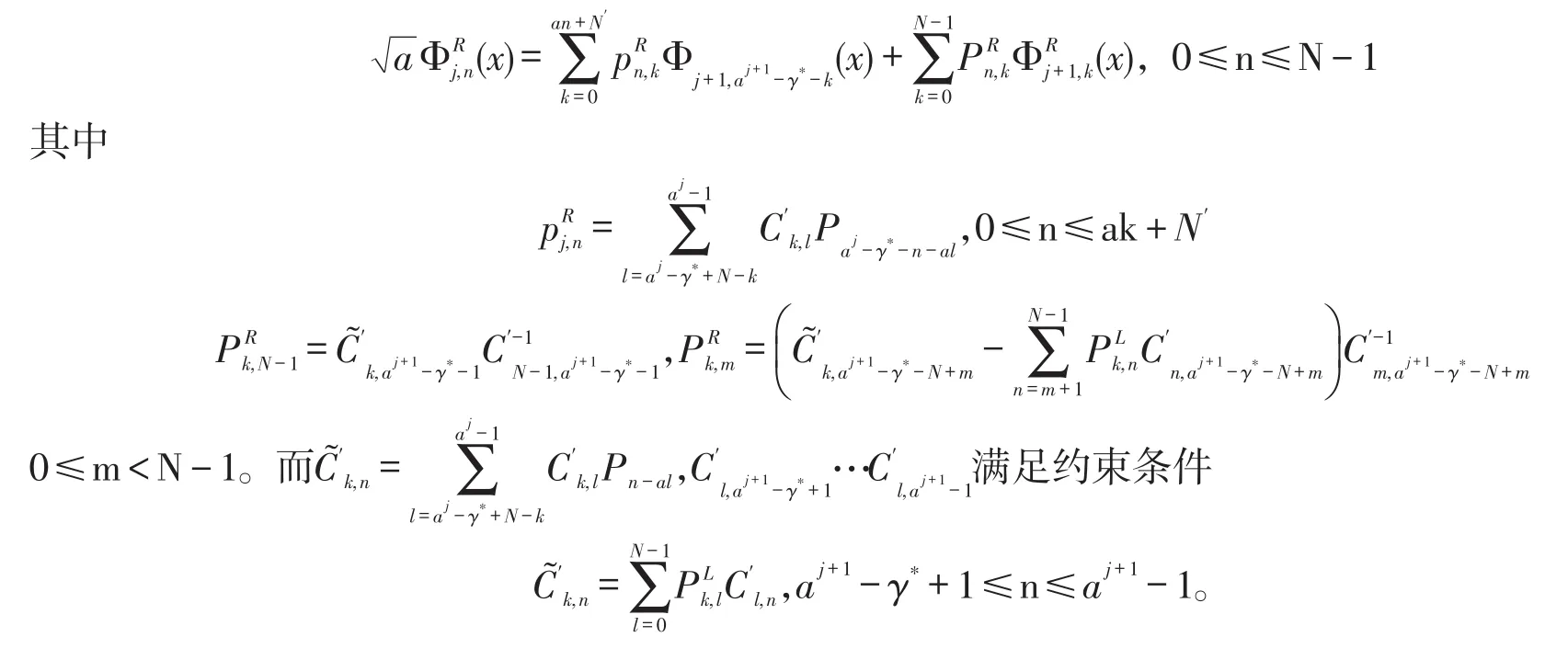
3 伸缩为a的L2[0,1]上多小波的构造

定理2设通过下列两尺度方程确定：

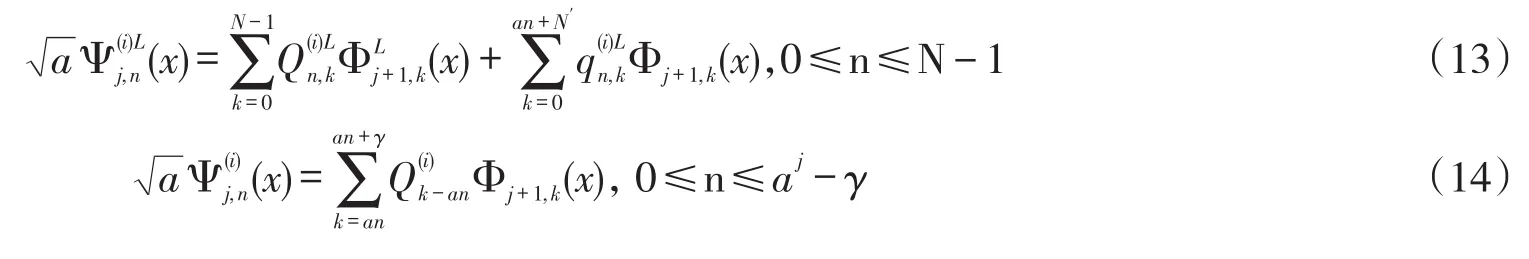
证明由

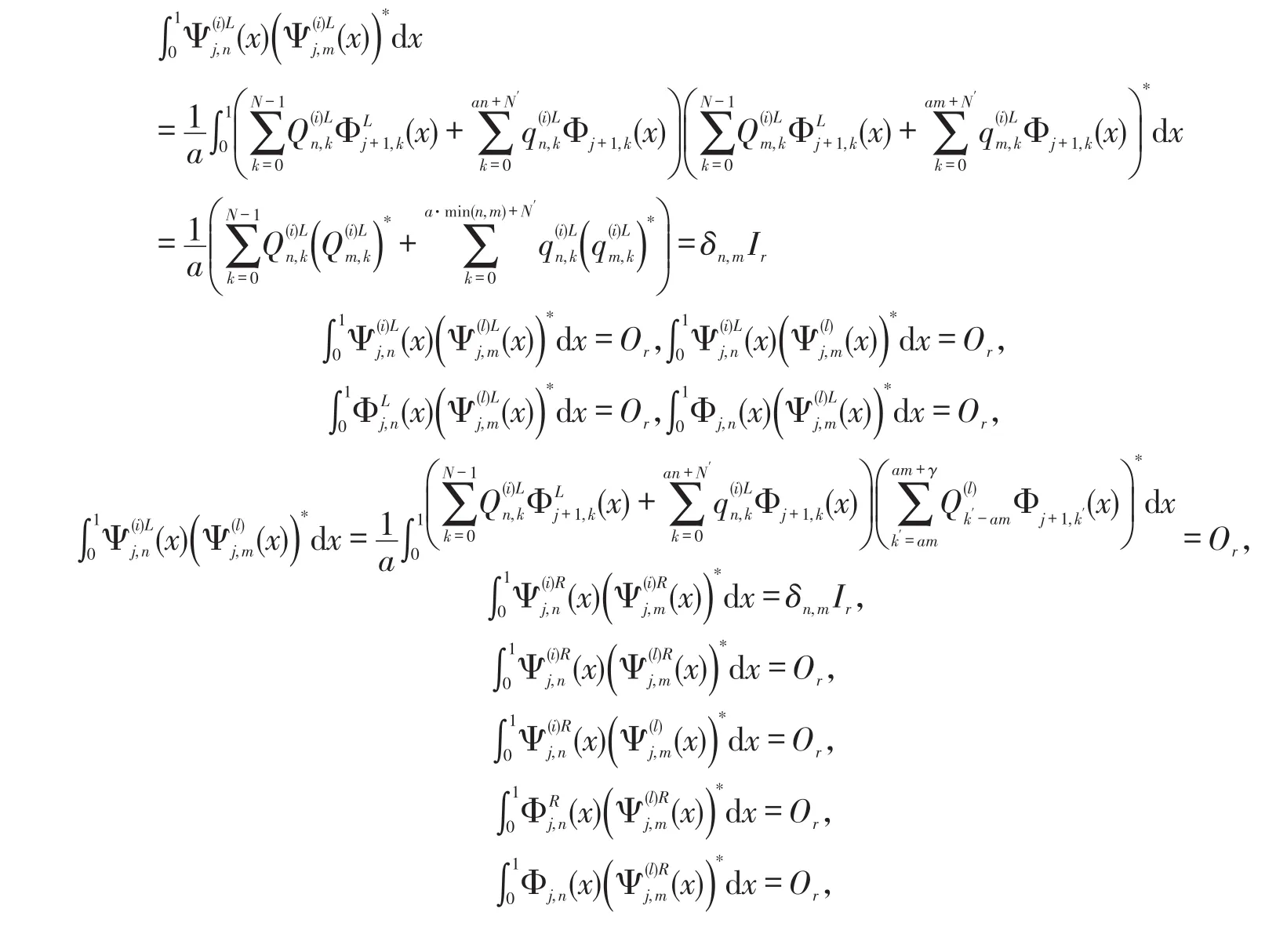
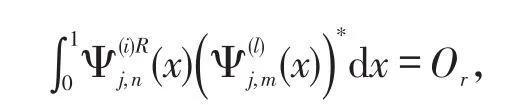
为了简单起见，定义下面几个符号：

（i）根据定理1中构造的多尺度函数的函数组定义

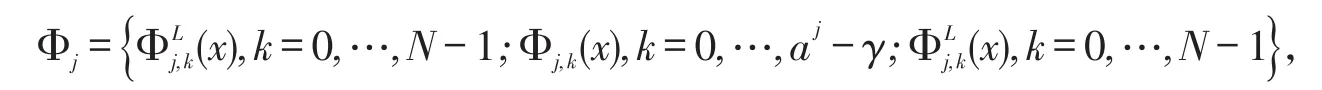
（ii）根据定理2中构造的多小波的函数组定义

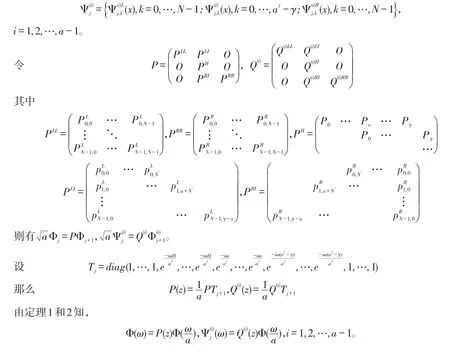
定理3 由定理1和定理2定义的Φj和满足（7）-（9）和（13）-（15）的两尺度方程，那么以下命题等价：

（i）Φj和是正交的多小波系统函数组；

证明Φj和是正交的多小波系统函数组等价于。

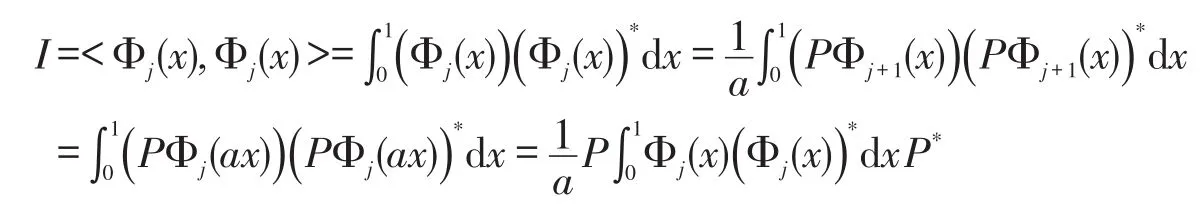
那么PP*=aI。同理有，

于是由P(z)，Q(i)(z)的定义。上述结论等价于

由定理3，需要构造Φj和是正交的多小波系统函数组，那么矩阵P和Q(i)要满足PP*=aI，PQ(i)*=O，，即有

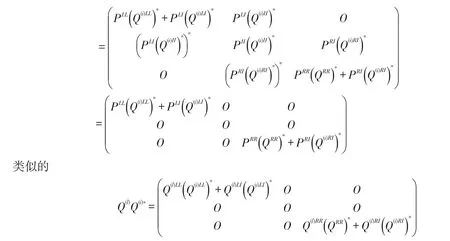
这样，构造了一组矩阵PLL,PLI,PRI,PRR和Q(i)LL,Q(i)LI,Q(i)RI,Q(i)RR。

整理这些左边界矩阵PLL,PLI,Q(i)LL,Q(i)LI和右边界矩阵PRI,PRR,Q(i)RI,Q(i)RR。为了使得PP*=aI，PQ(i)*=O，Q(i)Q(l)*=δi,laI，需要对这些矩阵做Schmidt正交化。

于是，构造下列矩阵序列

那么，有了的显式构造。

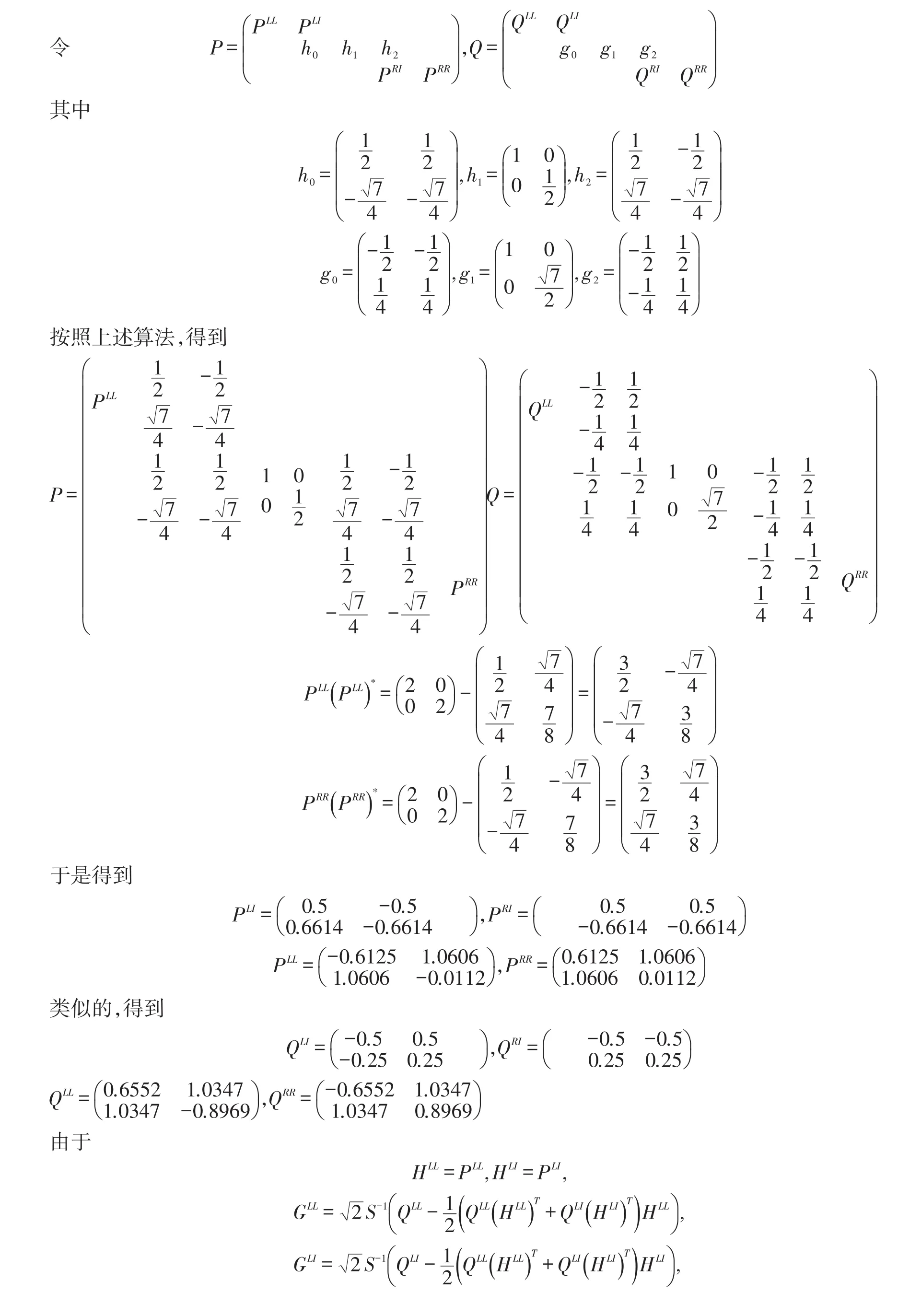
4 构造算例

利用2重C-L多尺度函数与多小波的面具构造区间多小波

可知，a=2,γ=2,N=1,N′=0

［1］杨守志，彭立中.基于PTST方法构造高阶平衡的正交多尺度函数［J］.中国科学E辑信息科学，2006，36（6）：644-656.

［2］李尤发，杨守志.Arm let多小波的构造算法［J］.数值计算与计算机应用，2007，（08）：290-297.

［3］C.Cabrelli，C.Heil，U.Molter.Accuracy of lattice translateofseveralmultidimensional re-n-able function［J］.JournalofApproximation Theory，1998，95（1）：5-52.

［4］Yang Shouzhi.Extension ofmultireslution analysis and the construction of orthogonalmultiwavelets［J］.Geogian Mathematical Journal，2005，12 （3）：561-571.

［5］ShouzhiYang.Youfa LiTwo-direction refinable function and two-directionwaveletwithdilation factorm［J］.Applied Math and Computation，2007，（13）：1908-1920.

［6］SUN Lei.CHENG Zhengxing，Construction of symmetric/antisymmetric compactly supported orthogonalmultiwavelets［J］.Mathematics in Practice and Theory，2008，（6）：169-174.

［7］Lian JA.Analysis-readymultiwavelets（Armlet）for processing scalar-valude signal［J］.IEEEProcessing Letters，2004，（11）：205—208.

［8］Lian JA.Armletand balancedmultiwavelets：flipping filter construction［J］.IEEETransaction on SignalProcessing，2005，53：1754—1767.

［9］冷劲松，程正兴，等.正交共轭滤波器的构造［J］.计算数学，2004，（10）：151-160.

［10］高协平，张钹.区间子波神经网络（I）-理论与实现［J］.软件学报，1998，9（3）：217-221.

［11］高协平，张钹.区间子波神经网络（II）-性质与模拟［J］.软件学报，1998，9（4）：245-250.

The Construction of a Class of In terval Multi wavelet with Dilation a

ZHANG Jian-ji1,WANG Gang1，ZHOU Xiao-hui2

（1.SchoolofMathematical Science，Xinjiang Normal University，Urumqi，Xinjiang，830054，China；2.Information Science Branch,Oriental Institute,Zhejiang University ofFinanceand Economics,Jiaxing, Zhejiang,314400,China）

The interval Multiwavelets research isa hot issue in the study ofwaveletanalysis.How to construct a good nature（such as：compact support，high vanishingmoments，etc.）interval multiwavelets is the focus of research.In this paper，We give a constructionmethod to construcct the intervalmultiscale functions and Multiwaveletswith dilation factoraon［0，1］，and alsoweofferanumericalexample.

Intervalmultiwavelet；Dilation factor；Orthogonality

O174.2

A

1008-9659（2016）04-0020-11

2016-10-04

张建基（1989-），男，甘肃武威人，硕士研究生，主要从事小波分析及其应用方向研究。

*［通讯作者］周小辉（1986-），男，江苏常州人，硕士研究生，讲师，主要从事微分几何与小波分析方向研究。