高阶中立型泛函微分方程周期解的存在性

汪代明，倪前月

（1.阜阳师范学院 数学与统计学院，安徽 阜阳 236037；2.阜阳市第二中学，安徽 阜阳 236000）

高阶中立型泛函微分方程周期解的存在性

汪代明1，倪前月2

（1.阜阳师范学院 数学与统计学院，安徽 阜阳 236037；2.阜阳市第二中学，安徽 阜阳 236000）

运用相关文献的引理与 Mawhin重合度拓展理论，对一类高阶中立型方程(x(t)-cx(t-r))(n)+h(x′(t))+f(x(t))x′(t)+g(t,x(t-τ(t)))=p(t)进行了研究，得到了该方程至少存在一个T周期解的一组新条件。

周期解；重合度；高阶中立型泛函微分方程

由于在经济学、生物学和人口动力系统等实际问题中广泛应用，微分方程周期解存在性一直是众多研究者所关注问题[1-9]。杜波，鲁世平在文献[8]中讨论了二阶方程

周期解存在性条件，本人也在文献[9]中讨论了高阶方程

周期解存在的充分条件。考虑到中立型方程比非中立型微分方程更具一般性，研究结果也更有实际意义，当然其周期解存在性研究难度自然会大大增加。本文研究高阶中立型微分方程

的周期解，使用Mawhin重合度理论，得到了方程（3）在n≥2的情况下周期解存在的一组新条件，文献[8-9]的主要定理得到了推广。本文假设c,r为常数且|c|≠1，τ(t),p(t)为T周期函数，h,f,τ,p:R→R与g:R×R→R是连续函数，g(t,x)是t的T周期函数。

1 主要引理

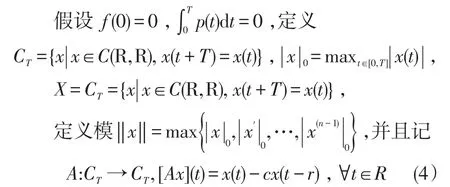
引理1（Mawhin重合度拓展定理[10]）设X,Y是Banach空间，L：Dom（L）⊂X↦Y是指标为零Fredholm的算子，Ω⊂X为有界开集，N:X↦Y在上是L-紧的.若下列条件：

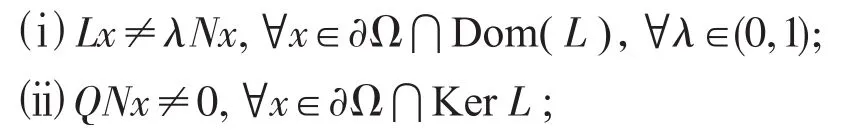
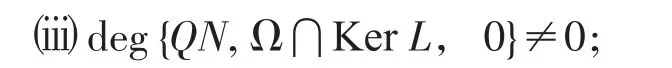
满足，则方程Lx=Nx在⋂Dom(L)上至少存在一个解。

引理2[11]如果|c|≠1，那么算子A存在唯一有界连续逆，且满足下列条件：

引理3[11]设x(t)∈Cm(R,R),m≥2,并且存在常数T＞0，使得t∈R有x(t+T)=x(t),则存在与x(t)无关的Mi＞0，使得

其中，当m为偶数时，

当m为奇数时，

其中，诸Bm-2s,B2m-4s,Bm-2s-1,B2m-4s-2是伯努数，可由如下递推公式求得

显然，Mi(m)＜Tm-(i+1)。

2 主要结果

定理1若以下条件

成立，其中常数r1≥0,r2≥0,K1,K2,D为正常数，则方程（3）至少有1个T周期解存在。

证明考虑方程

设上述方程（5）的任一T周期解为x(t)，由，并对该方程两边同在[0,T]积分，有

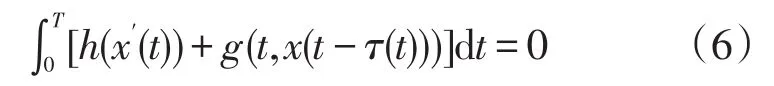
由中值定理知∃ξ∈[0,T],使得

下面先证存在t∗∈[0,T],使得

第一种情形：r1=0。若|x(η-τ(η))|＞D，则由式（7）和定理1条件得显然矛盾，故

第二种情形：r1＞0。若|x(ξ-τ(ξ))|＞D，则同样由式（7）和定理1条件，得

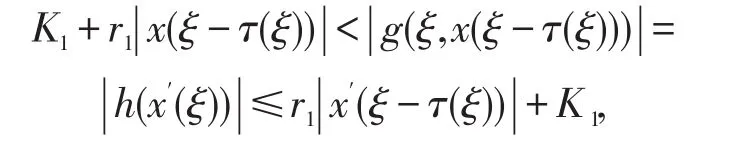
所以

总之，根据（9）（10）式，不管r1=0还是r1＞0，都有

又因ξ-τ(ξ)∈R,所以一定存在整数k和t∗∈[0,T],使得ξ-τ(ξ)=kT+t∗,从而由（11）式，得

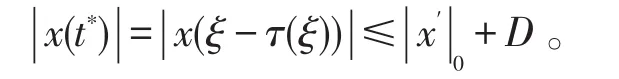
可见（8）式成立，因此有

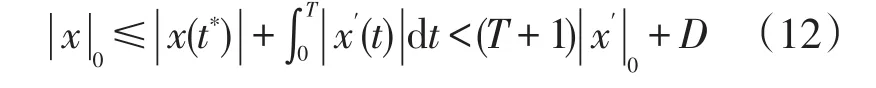
不妨令

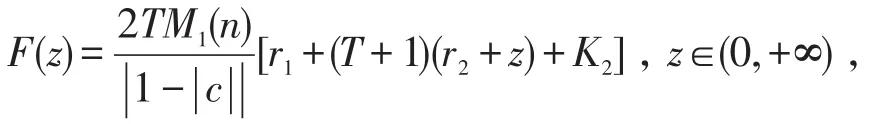
对上述ε＞0，由定理条件（IV）知，一定存在与λ和x无关的常数ρ≥D，使得当x＜-ρ时，有

由（7）式得，

由引理3，知

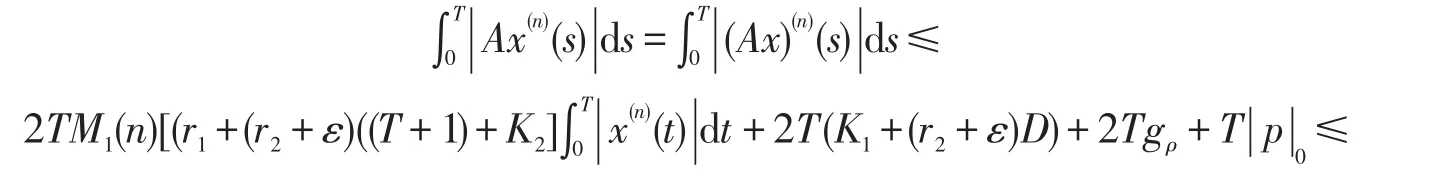
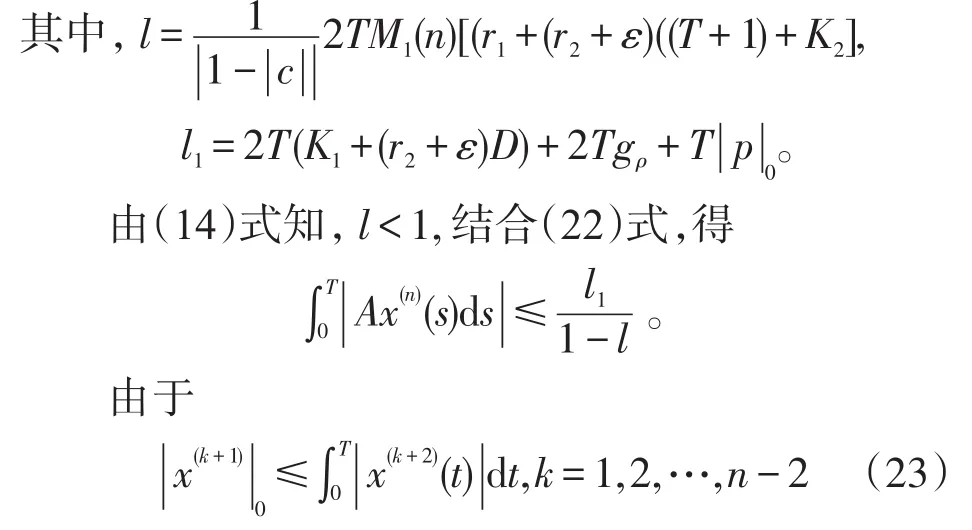
令（23）式中k=n-2，并结合引理2的条件，知

由引理3，可知

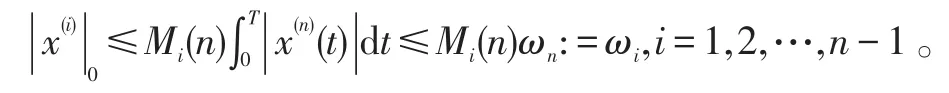
又考虑(12)式，有

显然ω0,ω1,…,ωn-1都是与λ和x无关的常数。取M=max{ω0,ω1,…,ωn-1}.令

显然KerL=R。定义投影算子P和Q分别为：

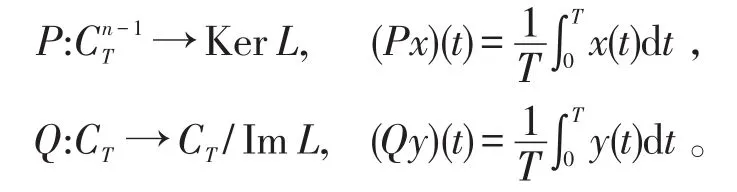
则 KerL=ImP,KerQ=ImL。L是指标为零Fredholm 的算子，且N在上L-紧。∀x∈∂Ω⋂Dom(L)和∀λ∈(0,1)有Lx≠λNx。显然，引理1条件满足。又对 ∀x∈∂Ω⋂KerL，则当x=M+1(＞D)或者x=-(M+1)(＜-D),于是由定理1条件得

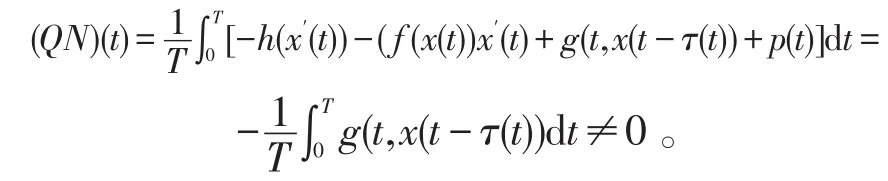
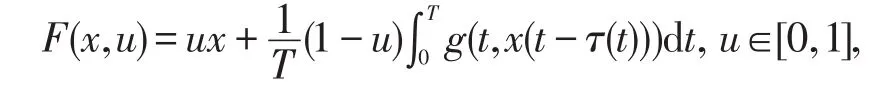
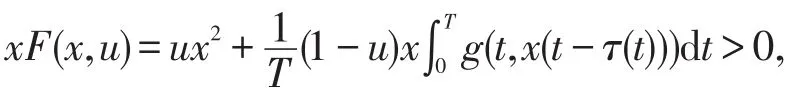
故F(x,u)是同伦映射，所以

显然，引理1三条件皆满足，所以本文所研究方程（3）至少有一个T周期解存在得证。

推论1用下列条件代替定理1中条件，则定理1的结论仍成立：

与定理1证明类似，也可得以下定理：

定理2若以下条件成立：

则方程（3）至少有1个T周期解存在，其中，常数r1≥0,r2≥0,K1,K2,D为正常数。

3 实例

考虑方程

其中

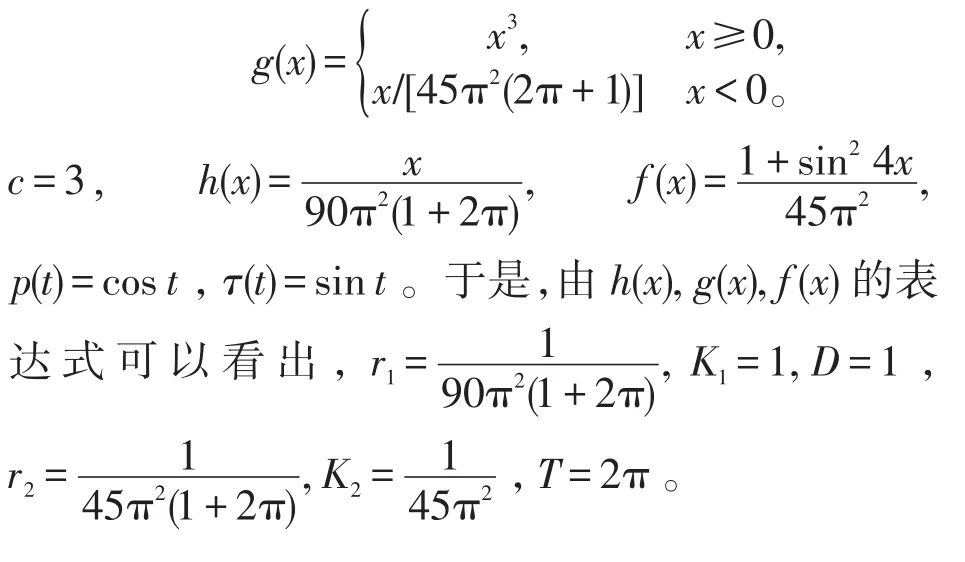
进而由引理3知

因此，定理1的推论的五个条件均满足。根据推论1，方程（24）式至少有1个T周期解存在。显然上述结论并不能由文献[8]或[9]得出，况且文献[9]和文献[8]分别为本文研究方程（3）的c=0及c=0,n=2的特殊情形，因此本文的讨论推广和改进了文献[8-9]的主要定理。

[1]Liu X Y.Existence of three positive solutions of neutral functionl difference[J].Chinese Quarterly Journal of Mathematics,2015,30(2)：172-183.

[2]武跃祥，武 钢．二阶中立型泛函微分方程的周期解[J].数学的实践与认识，2014，44（24）：311-315.

[3]罗芳琼，姚晓洁，秦发金.一类具多个偏差变元的二阶中立型泛函微分方程的周期解[J].数学的实践与认识，2012，42（20）：167-175.

[4]罗芳琼，姚晓洁，秦发金.一类具有偏差变元的高阶中立型Rayleigh方程周期解的存在性[J].数学的实践与认识，2012，42（22）：189-197.

[5]陈文斌，高 芳，鲁世平.一类时滞微分方程周期解的存在性[J].四川大学学报(自然科学版)，2014，51（3）：455-458.

[6]汪代明，冯春华.一类时滞脉冲微分方程的3个正周期解[J].吉林大学学报(理学版)，2011，49（3）：391-396.

[7]汪小明，孙杨剑.一类具偏差变元的高阶泛函微分方程周期解[J].西北师范大学学报，2013，49（3）：16-19.

[8]杜 波，鲁世平.一类具有偏差变元的二阶微分方程的周期解[J].数学研究，2007，40（1）：16-21.

[9]汪代明.一类具有偏差变元的高阶泛函微分方程的周期解[J].阜阳师范学院学报（自然科学版），2015，32（4）：25-28.

[10]Gains R E,Mawhin J L.Coincidence degree and nonlinear differential equations[M].Heidelberg：Springer-Verlag,1977.

[11]李晓静.具偏差变元的高阶中立型泛函微分方程的周期解存在性问题[J].纯粹数学与应用数学，2007，23（3）：394-401.

Existence of periodic solutions for higher order functional differential equations

WANG Dai-ming1,NI Qian-yue2
(1.School of Mathematics and Statistics,Fuyang Normal University,Fuyang Anhui236037,China；2.The Second Middle School of Fuyang,Fuyang Anhui236000,China)

By using the lemma of related documents and the Mawhin coincidence degree theory，a kind of higher order functional differential equations as follows (x(t)-cx(t-r))(n)+h(x′(t))+f(x(t))x′(t)+g(t,x(t-τ(t)))=p(t) is studied,some new conditions on the existence of periodic solutions were given.

periodic solution;coincidence degree;high order neutral functional differential equation

O175.12

：A

：1004-4329（2016）04-001-05

10.14096/j.cnki.cn34-1069/n/1004-4329(2016)04-001-05

2016-08-19

安徽省高校自然科学研究项目（KJ2011Z290）资助。

汪代明（1979- ），女，硕士，副教授，研究方向：微分方程。