向家坝下长江干流长河段河道横剖面分形特征
2017-01-12倪志辉吴立春
倪志辉,周 舟,吴立春,钟 亮,赵 健
(1.重庆交通大学水利水运工程教育部重点实验室,重庆 400074;2.重庆交通大学国家内河航道整治工程技术研究中心,重庆 400074;3.重庆交通大学西南水运工程科学研究所,重庆 400016; 4重庆第二师范学院,重庆 400067)
向家坝下长江干流长河段河道横剖面分形特征
倪志辉1,2,3,周 舟1,吴立春4,钟 亮2,赵 健3
(1.重庆交通大学水利水运工程教育部重点实验室,重庆 400074;2.重庆交通大学国家内河航道整治工程技术研究中心,重庆 400074;3.重庆交通大学西南水运工程科学研究所,重庆 400016; 4重庆第二师范学院,重庆 400067)
以长江干流向家坝—朱沱河段内局部碍航滩段为研究对象,建立二维非恒定-分形数学模型,统计满足最低维护水深的航道宽度,计算河道横剖面分维数,显示其呈1阶分维特性。河流宽度分维数和水深以及与所在河段、所在断面的形状有很大关系,一般浅滩呈现宽度分维数随水深增大而增大的趋势,横剖面分维数随流速增大整体上呈逐渐减小的趋势。对比同一河段内各滩分维数的大小,在上游流量相同时,河道横断面地形越平顺横剖面分维数越小。
分形维数;横剖面分形;数值模拟;非恒定流;通航水力要素;向家坝;长江
分形理论(fractal theory)是由Mandelbrot[1]于20世纪70年代率先提出并创立的一种探索自然界复杂形态的数学分支。Mandelbrot试图用这种方法描述自然界中的一些传统欧氏几何无法描述的复杂对象,例如弯曲的河流、复杂的海岸线等。分形维数是描述分形集几何特征的定量参数,能够反映分形的基本特征。流域水系、水网等地貌形态也具有分形特征。Nikora[2]对苏联境内多条河流平面形态的分形结构进行了研究,得出河道平面形态在一定尺度内具有分形特征的结论;Rego等[3]用多重分形去趋势波动法研究了巴西一些河流的主要的复杂水波动,认为巴西河流水位可以从多重分形的角度得出规律;Movahed等[4]采用分形方法研究了河流的流量波动;Sapozhnikov等[5-6]提出了分析河道自相似性的新方法。地表水系是一种典型的分枝现象,这种分枝图像具有自相似性。Balkhanov等[7-8]从分形的角度对一些河流水系进行了研究;Horton[9]在对水系进行诸多研究的基础上,提出著名的Horton定律,目前研究表明世界上大多数河流满足Horton定律,也即他们都有自相似性;沈中原等[10]建立了多重分形计算模型,并将其用于流域地貌形态的分形量化研究;马宗伟等[11]提出河流水系形态可通过其分形特征来反映;白玉川等[12]对蜿蜒河流分维数做了一定研究;陈康宁等[13]基于分形理论构建了区域水资源系统脆弱性评价指标体系,并对河北省水资源系统的脆弱性进行了评价;武国正等[14]以乌梁素海实测资料为例,分析了分形理论在水体营养状况评价中的适用性;倪志辉等[15-19]将分形理论应用于河流垂线流速分布及水流掺混长度的研究上,并讨论了长江重庆主城河段河流长度的分维数与洪水的关系,得出同一河段,河流长度分维值越大,河流的泄洪能力越差,所对应洪水发生的可能性以及洪水的强度越大。此外Micheal等[20-23]近年来也在河流分形方面做了许多研究;假冬冬等[24]对弯曲河道数值模拟的研究进展进行了总结,并分析了优劣。
本文以长江干流向家坝以下至重庆朱沱水文站共长约270 km的河段为研究对象,在搜集大量实测地形资料的基础上,利用一维及二维数学模型计算河段的水流条件,并采用大量实测资料对进行验证,表明数模计算结果可以作为变维分形的数据,结合累计和变维分形的结果即纵、横剖面分形维数,确定研究河段航道通航的指标。针对局部重点滩险河段,通过建立二维非恒定-分形数学模型,统计不同水深条件下的河道宽度,采用累计和变维分形求解河道横剖面的分形维数。同时,分析横剖面分维数与通航水流条件之间的关系。
1 二维非恒定-分形数学模型
1.1 模型控制方程
连续性方程及ξ、η方向的动量方程分别为
(1)
(2)
(3)
式中:h为水深;H为水位;g为重力加速度;Cξ、Cη为正交曲线坐标系中的拉梅系数;ξ、η为正交曲线坐标系中的两个正交曲线坐标;u、v分别为沿ξ、η方向的流速;n为曼宁系数;σ为各个方向上的应力张量。
1.2 定解条件
初始条件为各节点上的初始水位、流速:
(4)
(5)
(6)
开边界给定水位或流量过程:
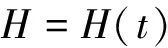
(7)
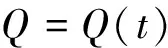
(8)
动边界采用冻结法处理,即在程序中设置干水深、淹没水深和湿水深3个特征水深,当某一单元的水深小于湿水深而大于干水深时,该单元只考虑质量守恒,不考虑动量守恒;当水深小于干水深时,单元被冻结,不参与计算;淹没水深用来检测单元是不是已经被淹没。
1.3 变维分形
Mandelbrot[1]将部分以某种方式与整体相似的形体定义为分形。分形分布满足如下关系式:
(9)
式中:s为欧氏长度;y为度量尺码;D′为分形维数;A′为比例常数。
对式(9)两端取自然对数得:
lns=lnA′-D′lny
(10)
在直角坐标系中lns-lny的图像为直线,用最小二乘法拟合该直线,它的斜率即为-D′,从而得到分形维数D′。
河道横剖面分维的物理意义是流量在河流横向长度方向的维数。因此,流量与河流宽度间也存在统一的自相似性:
(11)
式中:Q为流量;r为滩段最窄处河道宽度;D为河流横剖面分形维数,主要与流速、地形、水深等方面有关;A为比例常数。
D为常数的分形称为常维分形;若D与特征线度(这里的特征线度为河宽r)呈函数关系,则称之为变维分形。事实上,自然界中大量的复杂现象都需要用变维分形来描述,严格满足常维分形形式的现象是不存在的。维数是尺度变换下的不变量。许多学者对变维分形进行了研究,并提出了多种方法,如采用累积和系列变换分形的方法[18]、一维动态豪斯道夫分维数法[25]。本文采用由累计和序列获得的分维模型,称为“累计和分形”[18]。该方法的具体步骤如下:
步骤1 根据二维非恒定数学模型计算结果,统计各特征流量下满足一定河道水深的水面宽度,确定流量、河宽的原始数据对(Ni,ri),按N从小到大排列,i=1, 2, …,n(n为正整数)。
步骤2 以(N1,N2,N3,…)为基本序列,按下面的规则构造1阶累计和序列:
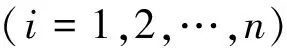
(12)
步骤3 建立1阶累计和的分段变维分形模型。双对数坐标中数据点(S1i,ri)和(S1i+1,ri+1)连线斜率的相反数D1i,i+1即为1阶累计和的分段变维分形的分维数。根据n个数据对,可以得到n-1条线段的分段变维分形的分维数,称之为分维数序列。
步骤4 将(S1i,ri)绘于双对数坐标中,并对该数据序列做线性拟合,所得直线斜率即相应河段的河流宽度分维数。
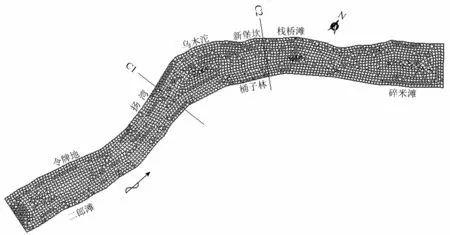
图1 栈桥滩计算网格
1.4 模型计算网格及验证
二维水流计算主要是在一维水流计算的基础上,模拟重点滩段在日调节非恒定流影响下河道的水流条件。在长约270 km的研究河段上,选取8个滩险河段,其中,水富—宜宾段2个,即栈桥滩和黄葱咀滩;宜宾—朱沱段取6个滩段:杨柳碛滩、过兵滩、金鱼碛滩、两条牛滩、白龙滩及磨盘石滩。
对选取的8个滩段分别建立模型,模拟河段平均长度在5 km左右,计算滩段范围、网格滩头概况以栈桥滩为例简要说明。
栈桥滩位于长江干流向家坝至宜宾航段内,下距宜宾合江门18.3 km,航道里程1 062 km。滩段左岸沟口为冲积滩,左岸土神沱等石盘与右岸周家碛、桐梓林边滩相对,致航槽弯、窄、险,故河段在枯中水期时,河道流态紊乱以致碍航。栈桥滩进口取在滩段上游二郎滩附近,出口取在滩段下游碎米滩附近,模拟河段约长5 km,计算网格采用三角形非结构网格,网格间距约30 m,共布置8 352个网格单元,3 009个网格节点,糙率根据流量的不同取0.033~0.035。计算网格如图1所示。
结合河段实测资料及一维非恒定数学模型计算值,根据所建立的二维水流数学模型对所选河段进行模型验证,通过水面线、断面流速分布等验证模型的合理性及其可靠性。
a. 水面线验证。流量为1 780 m3/s时栈桥滩及黄葱咀滩段水面线计算值与实测值的对比如表1和表2所示。
栈桥滩及黄葱咀滩的水面线计算值与实测值吻合较好,误差全部小于0.10 m,符合相关规范的计算精度要求。
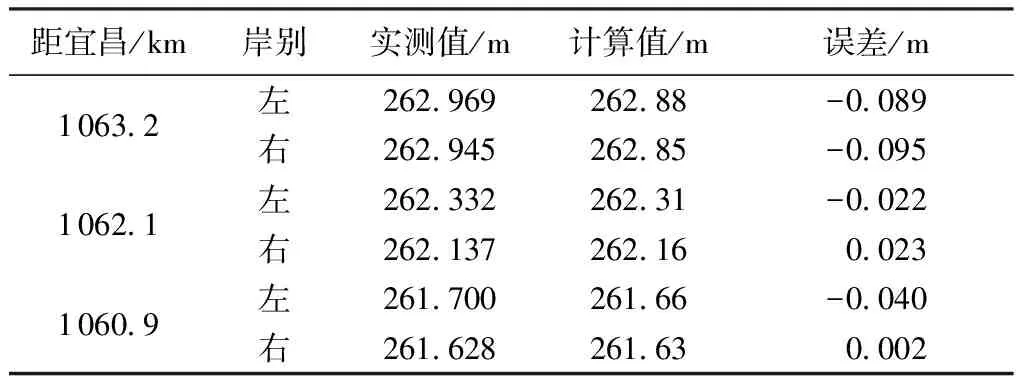
表1 栈桥滩二维数模水面线验证
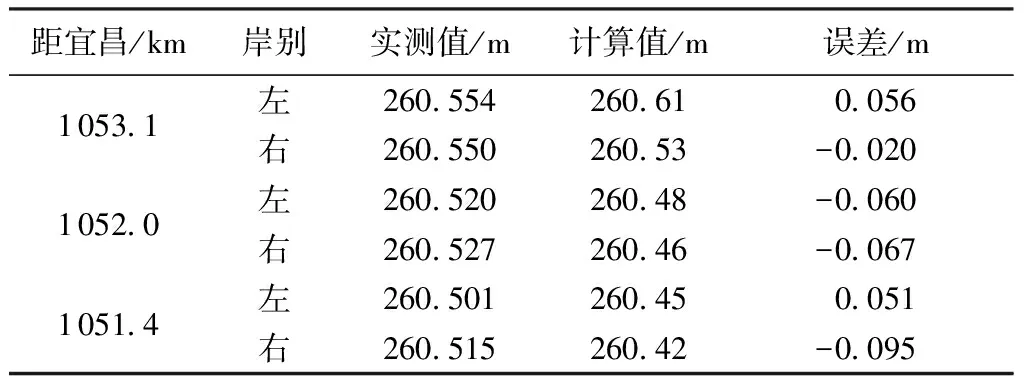
表2 黄葱咀滩二维数模水面线验证
其余滩段受实测资料缺少的限制,采用一维非恒定数学模型计算值对二维数学模型进行验证,验证结果与栈桥滩和黄葱咀滩的水面线验证结果相似,水位误差控制在规范要求的范围内,表明各计算河段均能满足与原型河道阻力相似的要求。
b. 流速验证。采用3个断面(栈桥滩段2个实测断面(图1中C1和C2)和黄葱咀滩段1个实测断面C3)的实测流速进行验证,验证结果见图2和图3。各测点流速计算值与实测值吻合较好,误差未超过15%,达到计算精度要求。
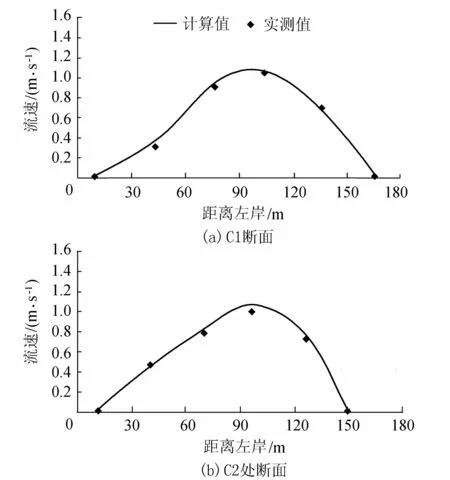
图2 栈桥滩河段断面流速分布验证(流量1 780 m3/s)
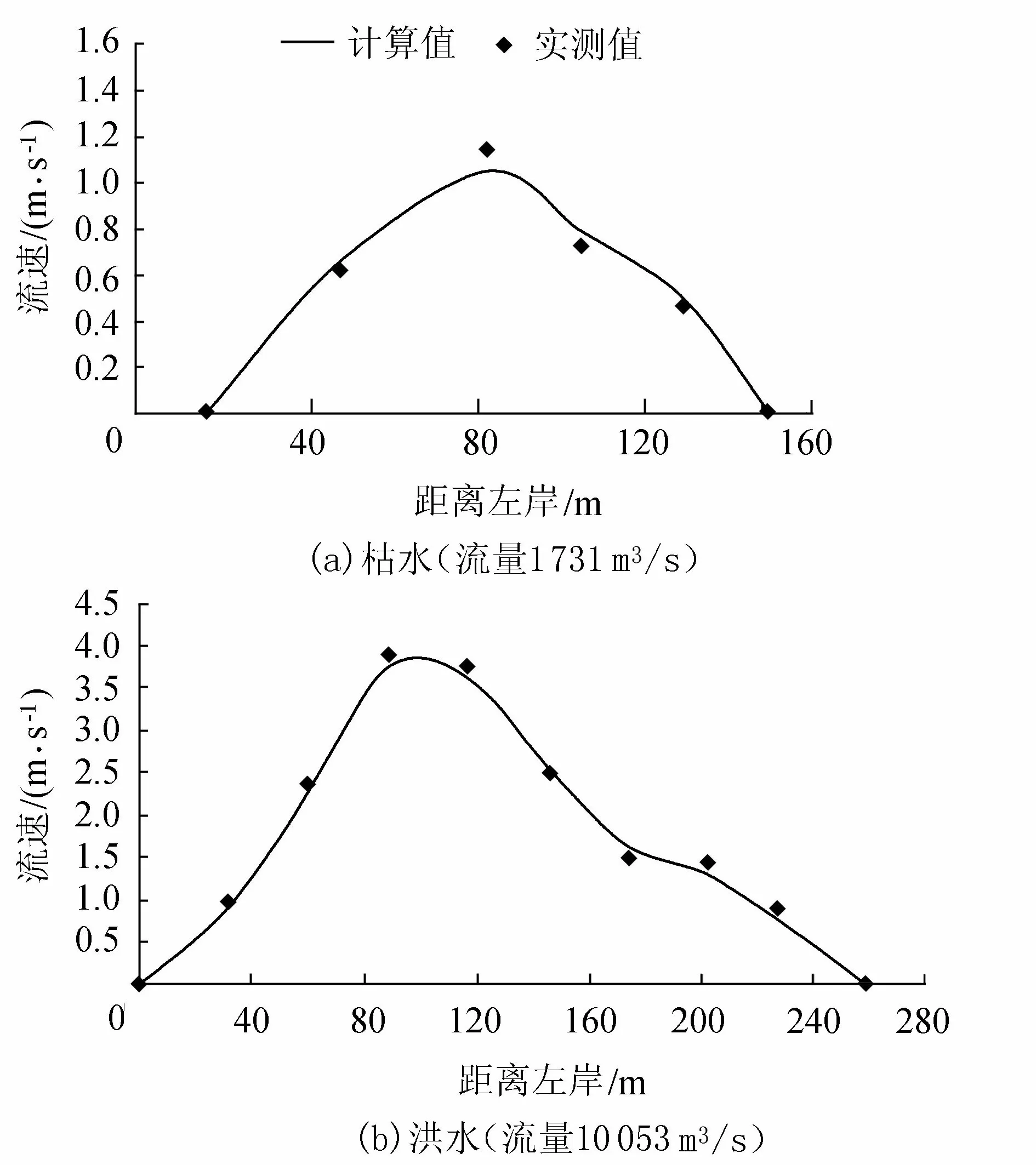
图3 黄葱咀河段C3断面流速分布验证
其余滩段结合一维计算所得左右岸流速值,对比验证相应流量下的二维数模岸边流速,验证结果与栈桥滩和黄葱咀滩的验证结果相似,流速误差控制在规范要求的范围内。
2 河道横剖面分维数
由于八个滩段分布在两个通航条件不同的航段上,其中栈桥滩和黄葱咀滩位于长江干流水富—宜宾航段,其余6个滩段位于长江干流宜宾—朱沱段。在现行航道尺度下,水富—宜宾航段与宜宾—朱沱航段最低维护水深不同,故按航道现状对8个滩险河段分两个航段探讨。
2.1 水富—宜宾航段
按航道现状统计满足最低维护水深要求的各特征流量的河宽,即统计栈桥滩和黄葱咀滩满足1.8 m最低通航水深时滩段最窄处河道宽度。为计算两个滩段横剖面分形维数,以栈桥滩为例,首先进行简单分形计算,结果见图4。从图4可以看出,各数据点明显不呈直线分布,说明栈桥滩河段河流宽度亦呈变维分形关系,需要采用变维分形模型对其进行处理。采用累计和变维分形的方法对该河段的河流宽度分形进行计算,计算过程见表3(在此只列出4级流量的计算过程,不过多赘述)。
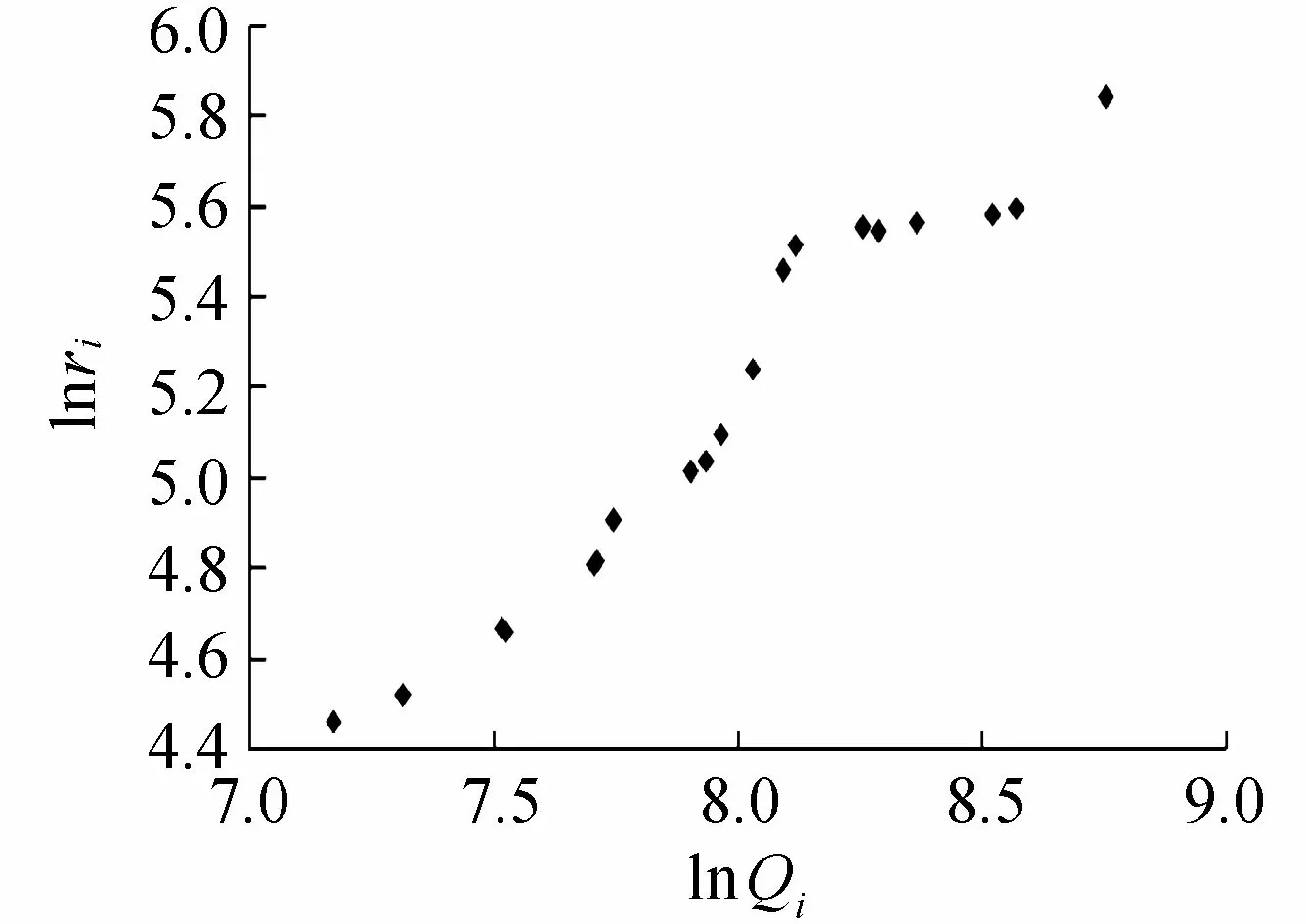
图4 栈桥滩河段河流宽度分维序列

流量Qi/(m3·s-1)宽度ri/mDi,i+1S1iD1i,i+1S2i13008648313001300150091996-23155752800-105897841001835106754-13548954635-10750428735185010569108135936485-106550915220
对黄葱咀滩进行同样的过程计算,最终计算汇总结果见表4及图5,可以看出,数据点与所拟合的直线吻合的很好,相关系数均大于0.99,说明各滩段的河流宽度具有一阶分维特性。

表4 水富—宜宾段各滩段河流宽度分维值计算结果
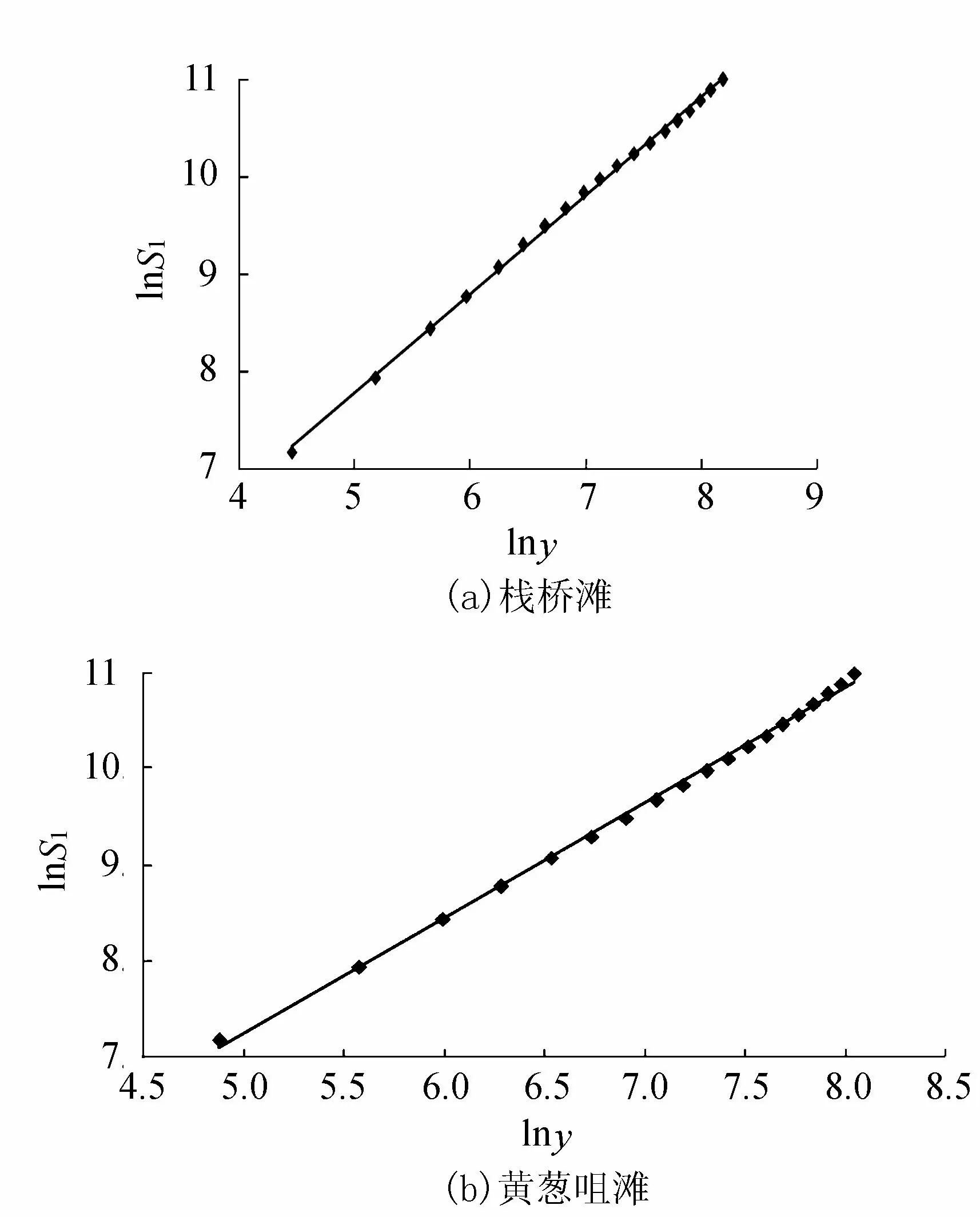
图5 水富—宜宾段河流宽度1阶累计和分维序列
2.2 宜宾—朱沱段
统计包括杨柳碛滩在内的6个滩段满足2.7 m最低通航水深要求时滩段最窄处河道宽度,计算6个滩段横剖面分形维数。以杨柳碛滩为例,由前述栈桥滩计算过程可知,横剖面分维数呈1阶分维特性,因此采用累计和变维分形的方法对杨柳碛滩的河流宽度分形进行计算,计算过程同表3。对其余5个滩段进行同样的计算,最终计算结果见表5及图6。可以看出,数据点与所拟合的直线吻合得很好,相关系数均大于0.99,说明宜宾—朱沱段内各滩段横剖面分维数具有1阶分维特性。
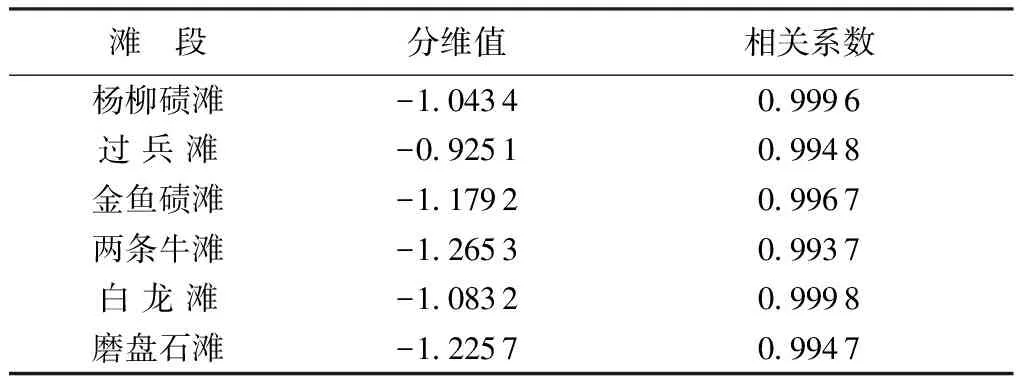
表5 宜宾—朱沱段各滩段河流宽度分维值计算结果
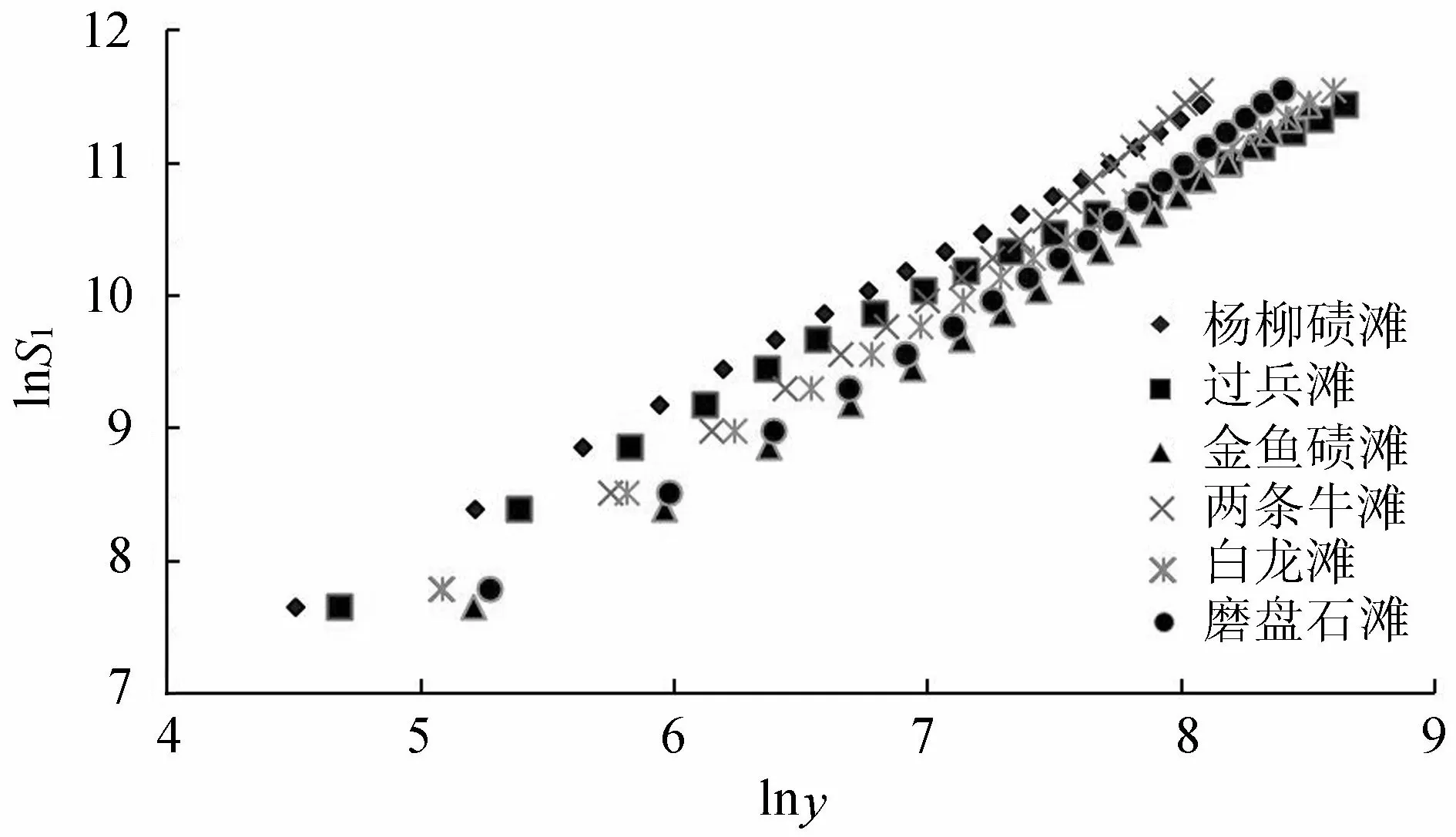
图6 宜宾—朱沱段河流宽度1阶累计和分维序列
2.3 不同水深下横剖面分维数
上述计算横剖面分维数的过程中,河道宽度取值为水富—宜宾段满足1.8 m水深的河宽及宜宾—朱沱段满足2.7 m水深的河宽。为讨论同河段下横剖面分维数与水深的关系,现对两个航段内的滩段不同水深下河道宽度分形维数进行计算,其中,水富—宜宾段统计满足2.7 m及3.5 m水深的河道宽度;宜宾—朱沱段统计满足3.2 m及3.5 m水深的河道宽度,计算结果见表6及表7。
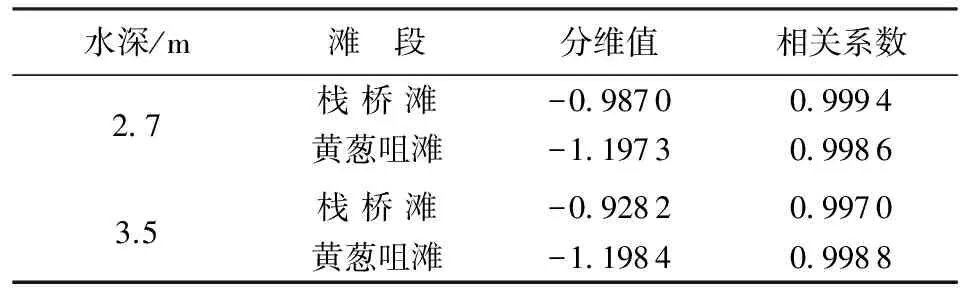
表6 水富—宜宾段各滩段分维值计算结果
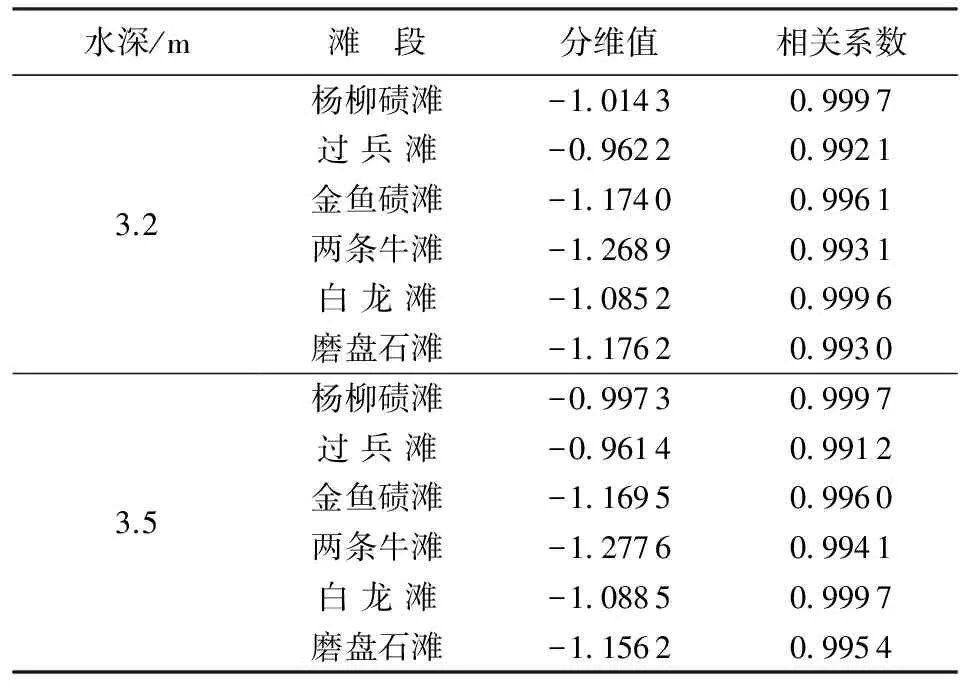
表7 宜宾—朱沱段各滩段分维值计算结果
3 分析与讨论
上述各滩险河段横剖面分形维数反映了满足一定水深的河道宽度与相应上游流量大小的相关程度。而满足特定水深的河道宽度受所在河段的横断面形状影响很大,因此从某种角度来说河道横剖面分维数反映的也是河道横断面形状与河道来流量的相关程度。而流量相同的情况下水深、流速的大小取决于所在河道横断面形状。
3.1 横剖面分维值
从表6、表7可以看出,天然河道的横剖面分维数存在着变维分形现象,同时可以发现,各滩段分维值都小于零,即为负分维数。分形理论的创始人Mandelbrot为描述多重分形系统的复杂性而引入了负分维。从数学上理解,它刻画空集“空”的程度,实质上是由系统的随机性产生的。负分维从一个侧面描述了系统的随机特性,反映了必然性与偶然性的内在联系,更具有普遍意义。负分维数的绝对值越大,表明自相似性越好。计算结果显示,长江干流水富—朱沱段各水深下的横剖面分维值在-0.928 2~-1.277 6之间,最大值出现在水深3.5 m时的栈桥滩(-0.928 2),最小值出现在水深3.5 m时的两条牛滩(-1.277 6)。水富—宜宾段较宜宾—朱沱段分维数要稍大,但并不明显。计算所得的相关系数均在0.99以上,表明河道横剖面河流宽度具有显著的1阶分维特性。
3.2 横剖面分维数与水深的关系
根据所得河流宽度分维数,同一河段不同水深河道横剖面分维数不同,同一水深不同河段的分维数也不一样,因此将统计的不同水深的滩险段河流宽度分维数及所在滩险河段类别及碍航成因列于表8及表9。由表可知,对滩险类别为浅滩的滩段,除白龙滩外,其余河段横剖面分维数均呈随水深增大逐渐增大的趋势;横剖面分维数随水深减小的滩段为两条牛滩和白龙滩,横剖面分维数随水深变化无规律的为黄葱咀滩和过兵滩,横剖面分维数随水深呈增大趋势的滩段为栈桥滩、杨柳碛滩、金鱼碛滩及磨盘石滩。栈桥滩、杨柳碛滩、金鱼碛滩及磨盘石滩4个滩段的地形具有一定的共性,其左岸或右岸均有一较大的浅滩,且河道深槽呈“V”形,相对较宽,例如图7中的杨柳碛断面及磨盘石断面。因此可推测得知,河道横剖面分维数大小和水深变化的关系与所在河段的地形有很大关联。
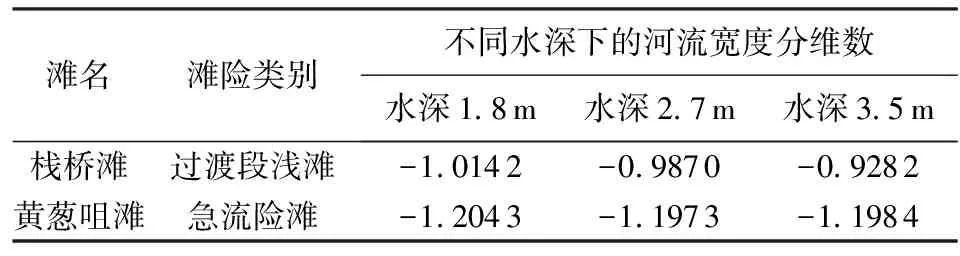
表8 水富—宜宾段滩险类别及相应 水深下河流宽度分维数
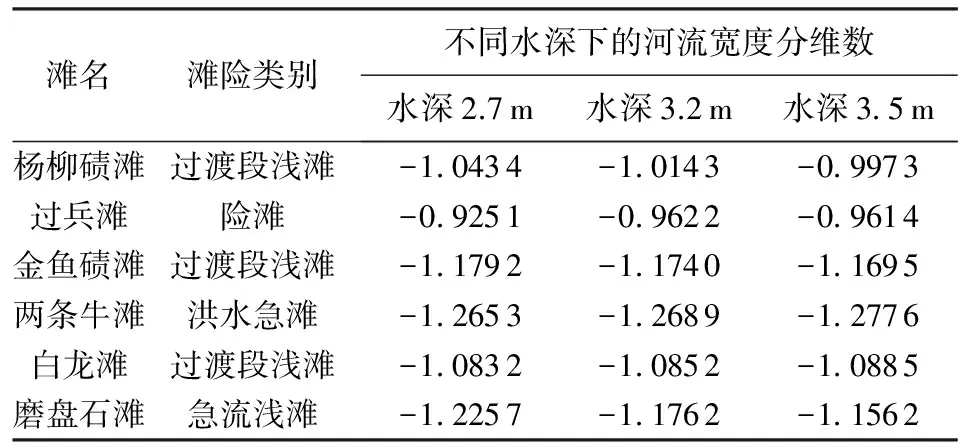
表9 宜宾—朱沱段滩险类别及相应 水深下河流宽度分维数
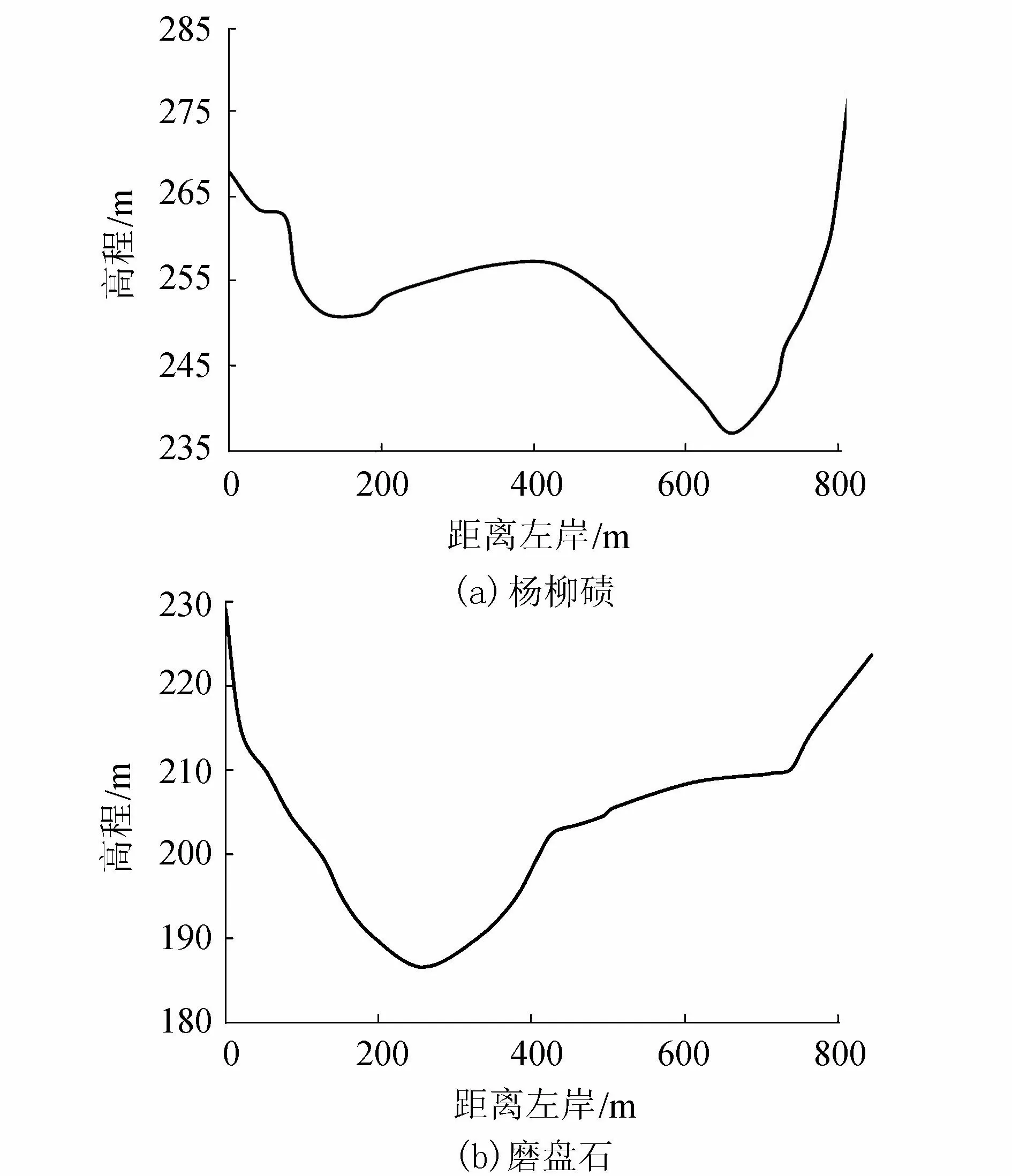
图7 杨柳碛滩及磨盘石滩河道横断面地形
河道横剖面分维数从某种角度来讲反映的也是河道横断面形状与河道来流量的相关程度,横断面形状越平滑,则相关程度越低,分维数越小。因此可以认为在上游流量相同时,横断面越平顺分维数越小。在水富—宜宾河段内,黄葱咀滩横断面形状相对栈桥滩要平滑,反映在图中,黄葱咀滩横剖面分维数在统一水深下平均比栈桥滩小20%左右。宜宾—泸州河段及泸州—朱沱河段等横断面相对平顺的滩段,其横剖面分维数也都相对较小。
3.3 横剖面分维数与流速的关系
各滩段平均流速基本随流量的增大呈线性增大的趋势。将各滩段平均流速与对应流量下的横剖面分维数一起绘于直角坐标系,如图8所示。图中横剖面分维数均为各航段内满足现行航道最小维护水深下的河流宽度分维数。
由图8可知,随着各滩段平均流速的增大(即流量的增大),除过兵滩外,其余滩段河道横剖面分维数虽有起伏变化但整体上呈逐渐减小的趋势。这种现象在黄葱咀和两条牛滩表现得极为明显,在流速均增大1倍的情况下(黄葱咀1.0 ~2.0 m/s,两条牛0.6~1.2 m/s),分维数都有60%~70%的增大。这是因为横剖面分维数表示的是河道流量与一定水深下河道宽度的相关程度。随流速减小,横剖面分维数逐渐变小意味着随流速减小(河道流量减小),河宽变化程度与流量变化程度之间的相关度逐渐下降。
4 结 论
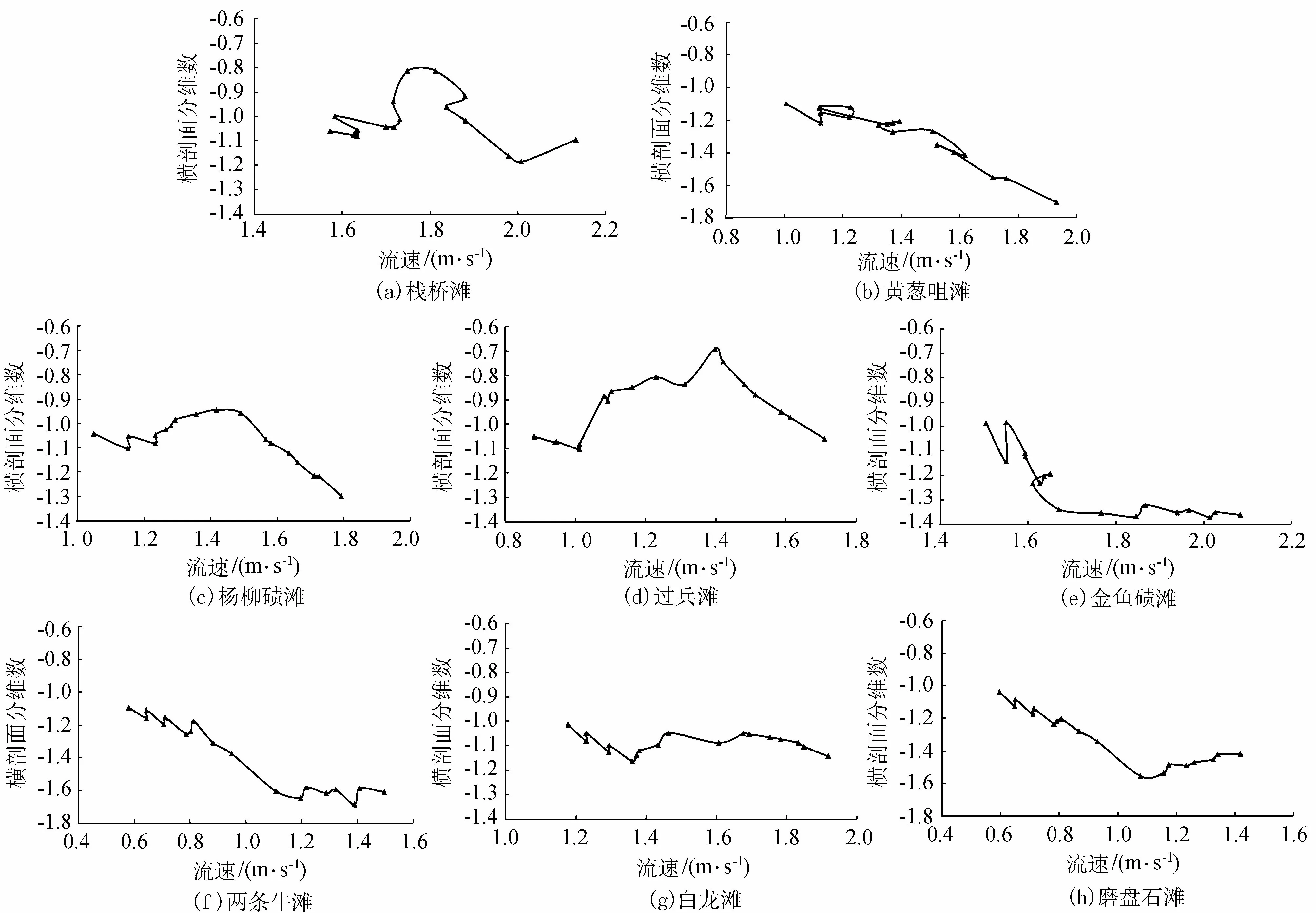
图8 水富—朱沱段各滩险段横剖面分维数与平均流速关系
a. 分维数拟合的相关系数均在0.99以上,说明河道横剖面河流宽度具有1阶分维特性。从某种角度来说河道横剖面分维数反应的是河道横断面形状与河道来流量的相关程度,发现河道横剖面分维数和水深的关系与所在河段、所在断面的形状有很大关系,一般浅滩呈现分维数随水深增大的趋势。
b. 除特殊地形外,一般横剖面分维数整体上随流速的增大呈逐渐减小的趋势。
c. 对比同一河流各滩段分维数的大小,上游流量相同时,河道横断面地形越简单平顺横剖面分维数越小。
[1] MANDELBROT B B.The fractal geometry of nature [M].San Francisco:Freeman,1982.
[2] NIKORA V I.Fractal structures of river planforms[J].Water Resources Research,1991,27(6):1327-1333.
[4] MOVAHED M S,HERMANIS E.Fractal analysis of river flow fluctuations(with Erratum)[J].A Statistical Mechanics & Its Applications,2006,387(4):915-932
[5] SAPOZHNIKOV V B,FOUFPULAGEORGOU E.Self-affinity in braided rivers[J].Water Resources Research,1996,32(5):1429-1439.
[6] FOUFPULA-GEORGOU E,SAPOZHNIKOV V B.Anisotropic scaling in braided rivers:an integrated theoretical framework and results from application to an experimental river[J].Water Resources Research,1998,34(4):863-867.
[7] BALKHANOV V K,BASHKUEV Y V.Fractal dimension of the channel network structure of Selenga River Delta[J].Water Resources,2004,31(2):148-151
[8] KUSUMAYUDHA S B,ZEN M T,NOTOSISWOYO S,et al.Fractal analysis of the Oyo River,cave systems,and topography of the Gunungsewu karst area,central Java,Indonesia[J].Hydrogeology Journal,2000,8(3):271-278.[9] HORTON R E.Erosional development of streams and their drainage basins,hydrophysical approach to quantitative morphology[J].Journal of the Japanese Forestry Society,1945,56(3):275-370.
[10] 沈中原,李占斌,李鹏,等.流域地貌形态特征多重分形算法研究[J].水科学进展,2009,20(3):385-391.(SHENG Zhongyuan,LI Zhanbin,LI Peng,et al.Multifractal arithmethic for watershed topographic feature[J].Advances in Water Science,2009,20(3):385-391.(in Chinese))
[11] 马宗伟,许有鹏,李嘉俊.河流形态的分形维数及与洪水关系的探讨:以长江中下游为例[J].水科学进展,2005,16(4):530-534.(MA Zongwei,XU Youpeng,LI Jiajun.River fractal dimension and the relationship between river fractal dimension and river flood: case study in the middle and lower course of the Yangtze River[J].Advances in Water Science,2005,16(4):530-534.(in Chinese))
[12] 白玉川,黄涛,许栋.蜿蜒河流平面形态的几何分形及统计分析[J].天津大学学报,2008,41(9):1052-1056.(BAI Yuchuan,HUANG Tao,XU Dong.Fractal and statistic analysis of planar shape of meandering rivers[J].Journal of Tianjin University,2008,41(9):1052-1056.(in Chinese))
[13] 陈康宁,董增川,崔志清.基于分形理论的区域水资源系统脆弱性评价[J].水资源保护,2008,24(30):24-34.(CHEN Kangning,DONG Zengchuan,CUI Zhiqing.Evaluation of vulnerability of regional water resources system based on the fractal theory[J].Water Resources Protection,2008,24(30):24-34.(in Chinese))
[14] 武国正,徐宗学,李畅游.基于分形理论的水体富营养状况评价及其验证[J].水资源保护,2012,28(4):12-16.(WU Guozheng,XU Zongxue,LI Changyou.Water eutrophication assessment and validation based on fractal theory[J].Water Resources Protection,2012,28(4):12-16.(in Chinese))
[15] 倪志辉,吴立春,张绪进,等.潮流流速垂线分布的分类及其分形规律[J].人民黄河,2012,34(3):13-16.(NI Zhihui,WU Lichun,ZHANG Xujin,et al.Patterns of vertical velocity profile of tidal current and their fractal law[J].Yellow River,2012,34(3):13-16.(in Chinese))
[16] 倪志辉.长江黄河垂线流速分布的分形研究[J].人民长江,2008,39(18):17-19.(NI Zhihui.Fractal study on vertical flow velocity distribution of the Yangtze River and the Yellow River[J].Yangtze River,2008,39(18):17-19.(in Chinese))
[17] 倪志辉,吴立春,舒小红.基于分形理论的挟沙水流掺混长度分析[J].人民黄河,2009,31(9):32-33.(NI Zhihui,WU Lichun,SHU Xiaohong.Carrying water mixing length analysis based on the fractal theory[J].Yangtze River,2009,31(9):32-33.(in Chinese))
[18] 倪志辉,张绪进,胥润生.长江黄河含沙量垂线分布的分形研究[J].人民长江,2011,42(19):73-76.(NI Zhihui,ZHANG Xujin,XU Runsheng.Fractal study on sediment concentration distributions in Yangtze River and Yellow River[J].Yangtze River,2011,42(19):73-76.(in Chinese))[19] NI Zhihui,WU Lichun,WANG Minghui.The fractal dimension of river length based on the observed data[J].Journal of Applied Mathematics,2013,51(8): 1-9.
[20] MICHEAL S,BOMMANNA G K,MONICA B E.The effect of bed age and shear stress on the particle morphology of eroded cohesive river sediment in an annular flume[J].Water Research,2008,42(15):4179-4187.
[21] 汪富泉,曹叔尤,丁晶.河流网络的分形与自组织及其物理机制[J].水科学进展,2002,13(3):368-376.(WANG Fuquan,CAO Shuyou,DING Jing.Fractal,self-organization and its physical mechanism of river networks[J].Advances in Water Science,2002,13(3):368-376.(in Chinese))
[22] 王卫红,徐鹏,田世民.分形理论在河型研究中的应用探讨[J].泥沙研究,2010,54(2):35-42.(WANG Weihong,XU Peng,TIAN Shimin.Application of the fractal theory in the river pattern study[J].Journal of Sediment Research,2010,54(2):35-42.(in Chinese))
[23] 周银军,陈立,欧阳娟.三峡蓄水后典型河段分形维数的变化分析[J].水科学进展,2010,21(3):299-306.(ZHOU Yinjun,CHEN Li,OUYANG Juan.Changes in fractal dimensions of representative reaches after the impoundment of Three Gorges Project[J].Advances in Water Science,2010,21(3):299-306.(in Chinese))
[24] 假冬冬,邵学军,周刚.弯曲河道横向摆动过程数值模拟研究进展[J].水利水电科技进展,2007,27(4):90-95.(JIA Dongdong,SHAO Xuejun,ZHOU Gang.Advances in numerical simulation of lateral migration of meandering channels[J].Advances in Science and Technology of Water Resources,2007,27(4):90-95.(in Chinese))[25] 宋立松.曹娥江低潮位序列突变成份分析[J].泥沙研究,2000,44(1):69-72.(SONG Lisong.Analyses on sudden change in low tide level series of the Caoe River[J].Journal of Sediment Research,2000,44(1):69-72.(in Chinese))
Fractal research of long river channel’s transverse section downstream Xiangjiaba Dam of Changjiang River//
NI Zhihui1, 2, 3, ZHOU Zhou1, WU Lichun4, ZHONG Liang2, ZHAO Jian3
(1.KeyLaboratoryofHydraulicandWaterwayEngineeringoftheMinistryofEducation,ChongqingJiaotongUniversity,Chongqing400074,China; 2.NationalEngineeringResearchCenterforInlandWaterwayRegulation,ChongqingJiaotongUniversity,Chongqing400074,China; 3.SouthwesternResearchInstituteofWaterTransportationEngineering,ChongqingJiaotongUniversity,Chongqing400016,China; 4.ChongqingUniversityofEducation,Chongqing400067,China)
Using a navigation-obstructing section downstream the Xiangjiaba Dam of Changjiang River as a research object, a two-dimensional unsteady fractal mathematical model that can meet the requirement for maintaining a minimum water depth was established for statistical analysis of the channel width, and the fractal dimension of the river channel’s transverse section was calculated, demonstrating one-order fractal dimension characteristics. The results show that the fractal dimension of the channel width has a close relationship with the water depth, the topography of river reach, and the shape of transverse section, demonstrating a general increasing trend of the fractal dimension of the channel width with the increasing water depth for a shoal and a general decreasing trend of the fractal dimension of the transverse section with the increasing flow velocity. Comparison of the fractal dimension of different shoals in the same river reach shows that the fractal dimension is relatively small for a transverse section with smooth topography under the same flow rate from upstream.
fractal dimension; fractal analysis of transverse section; numerical simulation; unsteady flow; navigable hydraulic elements; Xiangjiaba Dam; Changjiang River
国家重点基础研究发展计划(2016YFC0402104);重庆市基础与前沿研究计划(cstc2016jcyjA0380);内河航道整治技术交通行业重点实验室开放基金(NHHD-201514)
倪志辉(1980—),男,副研究员,博士,主要从事河流海岸水动力学研究。E-mail:benny251@163.com
10.3880/j.issn.1006-7647.2017.01.011
TU612.3
A
1006-7647(2017)01-0060-08
2015-12-04 编辑:郑孝宇)
