一类具有时滞脉冲的口腔恒化器模型的动力学性态分析
2017-01-12卢琨,曹慧,王莉
卢 琨, 曹 慧, 王 莉
(陕西科技大学 文理学院, 陕西 西安 710021)
一类具有时滞脉冲的口腔恒化器模型的动力学性态分析
卢 琨, 曹 慧, 王 莉
(陕西科技大学 文理学院, 陕西 西安 710021)
研究了一类单资源和两种微生物的时滞脉冲口腔系统的恒化器模型.利用脉冲微分方程比较定理、持久性理论和Floquet算子理论讨论了模型灭绝周期解的存在性;给出了灭绝周期解全局吸引性的临界条件;得到了系统持久性的充分条件.最后在满足条件θ1<1|θ2>1时,利用数值模拟结果说明本文的主要结论.
口腔系统; 恒化器模型; 时滞; 脉冲; 持久性
0 引言
在日常生活中,人类的口腔异味已经成为一种疾病,影响着人类的沟通交流,是人类社交中的一种障碍,也直接影响着人类的身心健康.随着口腔保健意识的提高,越来越多的人们开始重视这个问题.事实上,人类的口腔系统是一个生态系统,在这个生态系统中,存在着多种微生物,以及这些微生物生长、繁殖所需要的营养液.这些微生物存在于口腔中的不同部位,并且共同竞争和拮抗.当这些微生物的生长和繁殖出现不平衡时,就会出现口腔中的微生物生长失衡,从而引发口腔异味.
恒化器是一种用于连续培养微生物的实验室装置,可用于模拟湖泊和海洋中单细胞藻类浮游植物的生长,在工业上主要用于发酵过程和废水处理.也有一些学者将恒化器模型应用于研究人类的口腔系统,但是相关的研究很少.文献[1-4]中分别建立了口腔系统的恒化器模型,并对这些模型进行了理论和数值分析.但是这些模型没有考虑微生物在吸取了营养液之后进行转化所需要的时间滞后作用.
在本文中,将基于文献[5],建立一类具有时滞脉冲作用的恒化器微生物培养模型,并应用于研究人类的口腔系统.本文考虑的一类具有脉冲时滞的口腔系统恒化器模型如下:
(1)
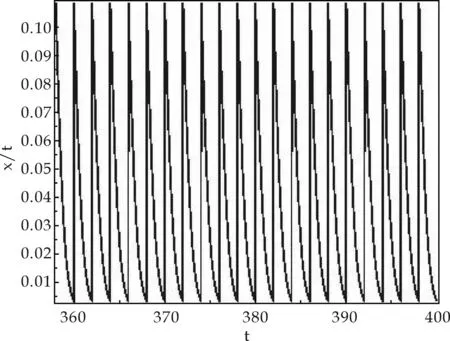
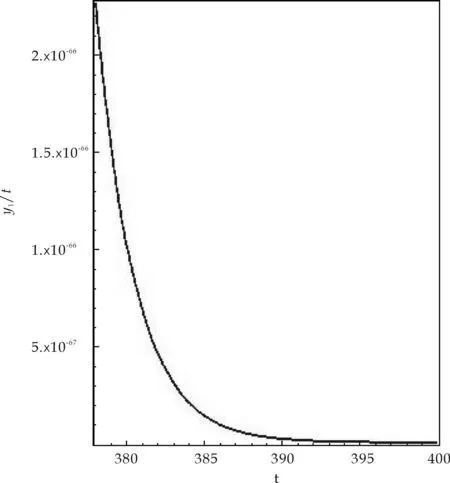
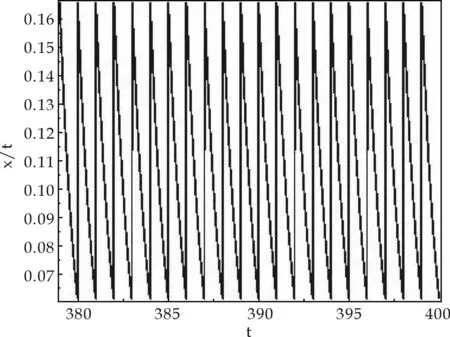
式(1)中:x(t)表示t时刻营养基的浓度,y1(t)和y2(t)分别表示t时刻口腔中微生物的浓度,x0表示进入口腔中的营养基的浓度.D是输出率,满足0 系统(1)的初始条件为 φi(0)>0,i=1,2,3. (2) 利用文献[6]中的方法,参考文献[7-12],首先给出一些有关时滞脉冲方程有用的引理和结论;接着,用脉冲微分方程比较定理、持久性理论和Floquet算子理论讨论模型的灭绝周期解的存在性,以及灭绝周期解全局吸引性的临界条件;最后,讨论系统的持久性. 1.1 定义 (2)V关于x满足局部Lipschitz条件. 定义2[14]若存在常数,M≥m>0,使m≤x(t)≤M,m≤y1(t)≤M,m≤y2(t)≤M对充分大的t成立,则称系统(1)是一致持续生存的. 1.2 部分引理 引理1 假设(φ1(t),φ2(t),φ3(t))>0,t∈(-τ,0),则系统(1)的解是严格正的. 引理2[13]令函数ω∈PC′([0,∞),R),满足以下不等式组 (3) 此处f(t),g(t)∈PC′([0,∞),R),fk(fk>0),gk,ω0是常数,对任意t>0有 引理3[15]考虑下面的时滞微分方程: 其中r1,r2,τ都是正数;x(t)>0,t∈[-τ,0].则有 1.3 微生物灭绝周期解的存在性 当y1(t)=y2(t)=0时,系统(1)可变为下面的系统 (4) 通过直接计算系统(4)就可得到下面的引理4: 1.4 微生物灭绝周期解的全局吸引性 证明:因为θ1<1,选择ε>0足够小,使得 (5) 由系统(1)可得, x′≤-Dx. 考虑下面的脉冲微分方程系统 (6) 令(x(t),y1(t),y2(t))是系统(1)具有初值条件(2)的解,且x(0)=x0>0,z(t)是系统(6)具有初值z(0+)=x0的解,由引理4可知,对于任意的ε>0,存在n1∈N,使得对于任意的t>n1T,有 (7) 由系统(1)的第2,3个方程,结合(7)可得 (8) 考虑如下的比较系统: (9) 由式(5)和(7)有μ1η 因为y1(s)=z2(s)=φ2(s)>0,y2(s)=z3(s)=φ3(s)>0,s∈[-τ,0],由微分方程比较原理和解的正性可知当t→∞时,y1(t)→0,y2(t)→0.因此存在足够小的正数ε1,ε2以及正整数n2(n2T>n1T+τ),对任意的t>n2T,y1(t)<ε1,y2(t)<ε2. (10) 1.5 持久性 首先证明系统(1)的所有解是一致有界的. 定理2 系统(1)的任意正解(x(t),y1(t),y2(t)),当t足够大时,存在一常数M>0,满足x(t)≤M,y1(t)≤M,y2(t)≤M. 证明:令V(t)=V1V2x(t)+V2y1(t+τ)+V1y2(t+τ),则V(t)∈V0. 沿系统(1)求导有 显然可以选择任意的K>0,满足 由引理2得 因此V(t)是最终有界的,故对系统(1)的任意正解(x(t),y1(t),y2(t)),当t足够大时,存在一常数M>0,使得x(t)≤M,y1(t)≤M,y2(t)≤M. 定理3 若θ2>1,则系统(1)是持久的.其中 证明: 假设(x(t),y1(t),y2(t))是系统(1)具有初值条件的任一解,由定理2有x(t)≤M,y1(t)≤M,y2(t)≤M. 由系统(1)有 考虑下面的比较系统 (11) 根据引理4有 利用比较原理及引理4,对足够小的ε4>0,有x(t)≥u(t)>u*(t)-ε4>0. 系统(1)的第2,3个方程可以改写成如下形式 (12) 定义 则Vi(t),i=1,2沿系统(1)解曲线的导数为 (13) (14) (15) 当t≥t0考虑下面的脉冲微分方程 (16) 根据引理4,系统(16)的正周期解为 因而有 (17) 结合(13)、(17)可得 (18) 以下只对(18)的第一个式子讨论. 以下证明对于足够大的t,有y1(t)≥m.分两种情况. 在这个部分,利用数值模拟的方法展示所得到的结论.取a1=0.1,a2=0.1,T=2,m1=0.2,m2=0.1,V1=0.3,V2=0.2,x0=0.5,y0=2,z0=1,x10=x0,y10=y0,z10=z0,γ=0.3,x0=0.35. 当D=0.5,可以得到θ1=0.066 44,满足定理1的条件.相应地可以得到图1、图2.由图1~2可知,当θ1<1时,微生物会灭绝. 图1 营养基x(t)的时间序列图 图2 微生物y1(t)的时间序列图 当D=0.046,θ2=2.368 7>1相应地可以得到图3、图4.由图3~4可知,当θ2>1时,微生物会持久生存. 图3 营养基x(t)的时间序列图 图4 微生物y1(t)的时间序列图 本文建立了一类具有时滞脉冲作用和Monod型功能反应函数的口腔系统恒化器模型.讨论了该模型微生物灭绝周期解的存在性;证明了微生物灭绝周期解的全局吸引性的临界条件;最后给出了系统持久的充分条件,也通过数值模拟的方式展示了理论结果. [1] 乔伟民,樊明文.口腔恒化器的研制[J].口腔医学纵横,1997,13(3):148-150. [2] 李鸣宇,刘 正.磷脂壁酸-葡糖基转移酶-葡聚糖相互作用对口腔链球菌粘附作用的影响[J].牙体牙髓牙周病学杂志,1994,4(2):70-71. [3] 杨坤一,信 鸽.改进的口腔微生物种群模型及其Lyapunov稳定性[J].数学的实践与认识,2012,42(23):157-163. [4] 李德懿,李宗林.可控模拟口腔环境的改良MD-300恒化器的建立及应用[J].临床口腔医学杂志,2002,18(4):243-245. [5] 阮士贵.恒化器模型的动力学[J].华中师范大学学报(自然科学版),1997,31(4):377-397. [6] 孙树林,张瑞娟.具有时滞和脉冲输入的一类双资源和两种微生物恒化器模型的分析[J].系统科学与数学,2012,32(1):111-120. [7] Zhang Y J,Xiu Z L,Chen L S.Chaos in a food chain chemostat with pulsed input and washout[J].Chaos,Solitons & Fractals,2005,26(1):159-166. [8] Xia H X,Wolkowicz G S K,Wang L.Transient oscillations induced by delayed growth response in the chemostat[J].Journal of Mathematical Biology,2005,50(5):489-530. [9] Meng X Z,Zhao Q L,Chen L S.Global qualitative analysis of new monod type chemostat model with delayed response and input in polluted environment[J].Applied Mathematics and Mechanics,2008,29(1):75-87. [10] 魏春金,陈兰荪.具时滞增长反应及脉冲输入Monod-Hakldane 恒化器模型的分析[J].南京师范大学学报,2008,31(3):6-11. [11] Wang F Y,Pang G P,Lu Z Y.Analysis of a Beddington-DeAngelis food chain chemostat with periodically varying dilution rate[J].Chaos, Solitions and Fractals,2009,40(2):1 609-1 615. [12] Miled E H,Alain R.Practical coexistence of two species in the chemostat A slow-fast characterization[J].Mathematical Bioscience,2009,218(1):33-39. [13] Lakshmikantham V,Bainov D D,Simeonov P S.Theory of impulsive differential equations[M].Singapore:World Scientific,1989. [14] 陈兰荪,陈 健.非线性生物动力系统[M].北京:科学出版社,1993. [15] Kuang Y.Delay differential equations with application dynamics[M].California:Academic Press Inc,1993. 【责任编辑:陈 佳】 Analysis of a class of oral chemostat model with time delay and pulse input LU Kun, CAO Hui, WANG Li (School of Arts and Sciences , Shaanxi University of Science & Technology, Xi′an 710021, China) An oral chemostat model with periodic pulse and time delay is discussed in this paper.Using the comparison theorem of impulsive differential equations,persistence theory and floquet operator theory,the existence of the microorganism-free periodic solution is proved,which is globally attractive under some critical conditions.Moreover,the sufficient conditions on permanence of the system is obtained.Finally,under the condition ofθ1<1|θ2>1,some numerical simulations are given to illustrate the main results. oral cavity system; chemostat model; delay; pulse; persistence 2016-07-12 国家自然科学基金项目(11301314); 陕西省教育厅专项科研计划项目(15JK1081) 卢 琨(1980-),女,陕西西安人,讲师,硕士,研究方向:生物数学 1000-5811(2017)01-0188-05 O175 A
1 主要结果

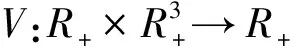

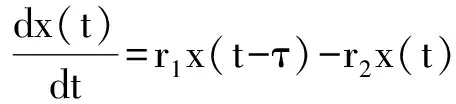


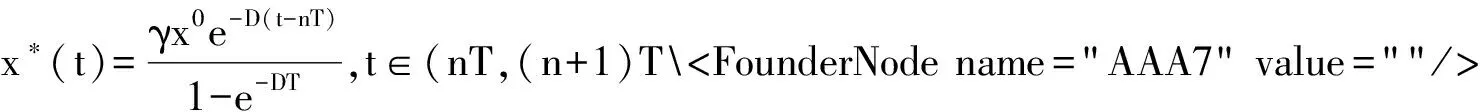
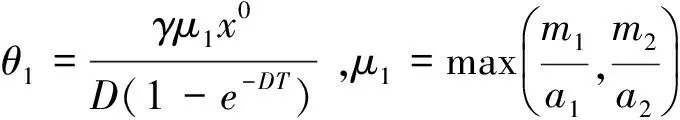
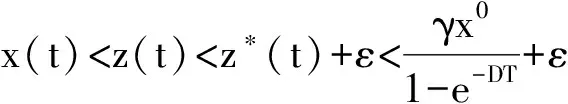

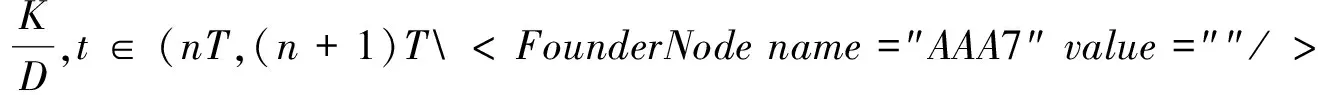

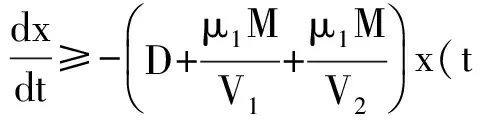

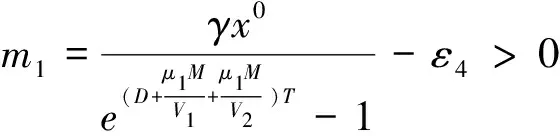
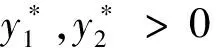


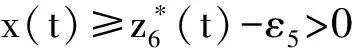

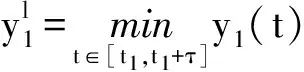
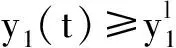



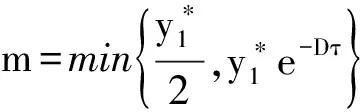
2 数值模拟

3 结论
