大规模MIMO系统中低复杂度的上行信号检测算法的综述

［龚明苇］

大规模MIMO系统中低复杂度的上行信号检测算法的综述

［龚明苇］

大规模多输入多输出（MIMO）是下一代多用户蜂窝系统的关键技术之一。我们要尽最大的努力找到合适的检测算法来保证高吞吐量数据的信号检测。对此研究了近几年来所提出的一些低复杂度的算法，并做了基本的介绍与分析。并且结合大规模MIMO出现的一些新特性，介绍了在新的算法中这些特性的作用，并且简单分析了因为这些新特性的出现而可能产生的优化算法的改进方向。

低复杂度 大规模MIMO 信号检测

龚明苇

重庆邮电大学通信与信息工程学院。

1 引言

MIMO(Multiple-Input Multiple-Output)技术指在发射端和接收端分别使用多个发射天线和接收天线，使信号通过发射端与接收端的多个天线传送和接收，从而改善通信质量。它能充分利用空间资源，通过多个天线实现多发多收，在不增加频谱资源和天线发射功率的情况下，可以成倍地提高系统信道容量，显示出明显的优势。然而，在目前典型的节点天线个数配置和小区设置的情况下，研究工作表明网络MIMO传输系统会出现频谱和功率效率提升的“瓶颈”问题。为此，研究者们提出在各节点以大规模阵列天线替代目前采用的多天线，由此形成大规模MIMO无线通信环境，以深度挖掘利用空间维度无线资源，解决未来移动通信的频谱效率及功率效率问题。 大规模MIMO无线通信通过显著增加基站侧配置天线的个数，以深度挖掘利用空间维度无线资源，提升系统频谱效率和功率效率。

但是，将大规模MIMO技术应用到实际的系统中将是一个不简单的任务，其中一个原因就是需要提出新的BS端的信号检测算法。因为传统MIMO中一些有效的算法在大规模MIMO中，其计算复杂度将会显著增高，在综合考量下（包括部署成本，检测功耗等），这些传统算法将不再适用（其计算复杂度是BS端不能忍受的）。例如，最优检测算法-最大似然估计（ML），虽然有着非常好的性能，但其计算复杂度是随着发送端天线数量成指数增长的，如果应用在大规模MIMO中，计算复杂度将是难以想象的地步，类似的还有一些非线性的次优检测算法：球形算法、M算法等。所以，我们不得不重新考虑线性检测算法，如近零算法（ZF）、最小均方误差算法（MMSE）等。但是传统线性算法又涉及到复杂的矩阵求逆的过程，其计算复杂度在大规模MIMO仍然很高。因此，我们不得不提出一些新的BS端的检测算法，或者优化方案来降低算法的计算复杂度，以此降低BS端的功耗，以达到可以在实际系统中应用的地步。

所以，本课题的研究意义在于对比各种优化算法，找出可行性方案，为未来的解决方案提供一些有价值的参考。

本文的结构如下：第2部分介绍关于本课题的研究现状以及主要的研究内容。第3部分介绍该课题目前存在的问题。第4部分未来关于该课题可优化的方案。

2 大规模MIMO中低复杂度的检测算法

2.1 国内外研究现状

目前，针对降低BS端算法计算复杂度的次优检测算法被提了出来。这些算法大致分为2类：非线性算法、线性算法及其变种。

非线性算法有局部搜索（LS）[8～10]，消息传送（MP）[7,11～13]，蒙特卡罗马尔可夫链（MCMC）[14]等一些算法。虽然这些算法能够得到比较好的性能，但是其计算复杂度还是很高（相当于或者高于MMSE检测）[2]，在实际系统中不适用。因此，低复杂度的线性检测及其变种是大规模MIMO系统中的候选算法，特别是BS端天线数量远大于UE数时[19]。线性算法及其变种。线性算法中主要以MMSE算法（相比ZF算法，同样要计算矩阵的逆，MMSE性能更好）为主，然后在其基础上进行各种优化或者提出新的改进。文献[3]提出了一种新的MMSE接收机-MMSE残余线性回归（LRR），通过学习线性回归模型，来提升MMSE的性能。LRR接收机通过导频数据来估计信道，然后利用本地生成的训练数据（不通过信道传输）来找到线性回归参数。LRR可以用于以后MMSE检测的性能提升。在文献[4]和[5]中，一种截断的诺伊曼级数展开被用来在MMSE检测中近似的求矩阵的逆，其性能与计算复杂度与所选择的诺伊曼级数的数量成比例。然而，一旦选择项数目K大于大于等于3的时候，其近似求逆的计算复杂度与传统求逆的复杂度相当，因此诺伊曼级数展开在K大于2的时候，将会失去优势[4]。文献[6]提出一种改进的MMSE算法，其原理是基于Richardson 迭代来避免求矩阵的逆，从而达到降低复杂度的目的。文中首次证明了在大规模MIMO中，MMSE算法的滤波矩阵是正定对称的[6]，基于此结论提出了改进算法，从而避免求逆。文献[2]中也提出了一种MMSE改进算法，也是基于大规模MIMO中MMSE滤波矩阵是对称正定这一结论[6]，同[6]类似，文章提出利用松弛迭代（RI）的方法来避免求矩阵的逆。同时，文献[2]还利用了文献[7]所提出的“信道硬化-利用消息传递”（CHEMP,利用信道硬化所提出的MP算法）算法，因为其接收机非常适用文献[2]中所提出的算法。

2.2 系统模型及基本原理

考虑一个多用户的大规模MIMO系统，其中有K个单天线用户，BS端有N个接收天线（K）。令表示所有用户的发送信号，表示信道增益矩阵，则接收信号表示为，，是维加性高斯白噪声（AWGN）。

在实值系统中，传统MMSE算法的信号估计表达式为：

2.3大规模MIMO中出现的新特性：

信道硬化：指的是随着天线数量的增加，MIMO信道的协方差相对于其均值来说增加的非常缓放甚至萎缩[15]。考虑一个Nr x Nt MIMO信道，当Nr、Nt比例保持不变，随着其天线数量的增加，MIMO信道矩阵的奇异值的分布对信道矩阵项的实际分布不敏感（只要分布项是独立同分布的i.i.d）[16]。信道硬化在大尺度的信号过程中有很多优势。例如，大系统的线性信号检测，需要大量的矩阵求逆。而大量的随机矩阵求逆可以通过一些系列展开来进行快速进行，例如文献[4]的诺伊曼系列展开。信道硬化可以使近似矩阵求逆在大尺度中有效的利用[7]。

对角占优：指的是矩阵主对角元素的模都大于与它同行的其他元素的模的总和。文献[17]证明了在大规模MIMO中，Gram矩阵以及W（所需逆矩阵）是对角占优的。事实上，对于i.i.d高斯信道H，文献[24]证明。其在文献[6]中有应用。

在上行大规模MIMO信号检测系统，MMSE滤波矩阵是对称正定的[6]。

2.4 主要算法介绍

2.4.1 非线性算法

非线性算法有局部搜索（LS）[8～10]，消息传送（MP）[7,11～13]，蒙特卡罗马尔可夫链（MCMC）[14]等一些算法。MP算法类中的因子图（FG）方法利用多天线间干扰的消息传递和高斯近似来减少计算复杂度。为了未来提升在高阶幅度调中Tabu搜索（TS）和FS的性能，一种混合算法被提了出来[12]。在文献[13]中，大规模MIMO中出现的分层置信传播、强迫收敛和节点选择方法被用来以后降低算法的复杂度。考虑在大规模MIMO中出现的信道硬化现象，一种叫CHEMP的接收机在文献[7]被提了出来，这种方法是直接估计（代替传统的估计H）。在文献[14]，一种改进的MCMC算法-随机MCMC被提了出来，被用来减轻在MCMC的拖延问题。

2.4.2 线性算法及其改进

（1）近似矩阵求逆

算法的核心点是只保留展开的前K项。之后就是数学方面的计算来得到。

这种近似求逆的方法受到所计算的展开项K（前K项）的个数的影响。从分析中可以看出，计算不同K值其性能与复杂度会有不同程序变化。当K值不大于2的时候，其计算复杂度为，但是其性能有较大损失（与传统MMSE相比）。当K值大于2的时候，性能有所增加，逐渐靠近传统MMSE的性能，K在5以上时，几乎达到了传统算法的性能，但是K从3以后，其算法复杂度增高为，之后随着K的增加，复杂度越来越高。

（2）迭代算法

① Richardson Method

文献[6]中证明了在大规模MIMO系统下，MMSE算法的滤波矩阵是正定对称的。对于的大规模MIMO系统，实值信道矩阵H是满秩的。所以，有唯一解。因此，对于任意的的非零向量r，有

则格拉姆矩阵G是正定的，又因为

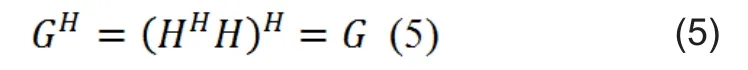
所以G也是对称的，因此G是正定对称的。所以我们可以利用Richardson方法在不求逆的情况下直接来估计发送信号，公式如下：

Richardson 方法(接收端的对数似然比LLR，从维特比解码中提取软输入[23])与传统MMSE相比（在取适当的初始值的情况下），迭代次数从2增加到3时，其性能增加比较明显，在次数为3的时候性能逐渐逼近传统MMSE；迭代次数从3增加到5时，性能也有所提升，提升比没有从2次到3次的明显，但是其性能已经基本与传统MMSE性能不相上下。其复杂度同RI的类似，由K的3次方降为K的2次方，且每次迭代次数增长所增加的计算复杂度为是固定

② Relaxation Iteration Method（RI）

文献[2]中利用文献[6]中证明的大规模MIMO下MMSE的滤波矩阵是对称正定的这一结论，提出了一种新的迭代方法，松弛迭代。利用W是对称正定的，将W进行分解：

则估计的传输信号s在第i次迭代时为：

RI在迭代次数为3的时候，性能是最接近传统MMSE的性能的，当迭代次数少于3时，性能有着比较明显的差距，其计算复杂度也仅仅是K的2次方（每次迭代次数增长所增加的复杂度为固定的），而在迭代次数大于3的时候，性能的提升比较缓慢，而复杂度又有增长，相比之下，3是最合适的迭代次数。同时该文献也对其迭代系数的取值进行了分析，在其值为1.02的时候，性能达到最优，即误码率最低。

1 T. L. Marzetta. Noncooperative Cellular Wireless with Unlimited Numbers of Base Station Antennas[J].IEEE Transactions on Wireless Communications,2010, 9(11): 3590-3600

2 GUO Ruohan, LI Xiaohui, FU Weihong, HEI Yongqiang. Low-Complexity Signal Detection Based on Relaxation Iteration Method in Massive MIMO Systems [J]. China Communications, 2015

3 S. Nagaraja, O. Dabeer, A. Chockalingam. LargeMIMO Receiver Based on Linear Regression of MMSE Residual[C].78th IEEE Vehicular Technology Conference, Las Vegas: IEEE Press,2013: 1-5

4 M. Wu, B. Yin, G. Wang, et al. Large-scale MIMO Detection for 3GPP LTE: Algorithms and FPGA Implementations[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 916-929

5 B. Yin, M. Wu, C. Studer, et al. Implementation Trade-offs for Linear Detection in Large-scale MIMO Systems[C].The 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver: IEEE Press, 2013: 2679-2683

6 X. Gao, L. Dai, C. Yuen, et al. Low-complexity MMSE Signal Detection Based on Richardson Method for Large-Scale MIMO Systems[C].80th IEEE Vehicular Technology Conference, Vancouver: IEEE Press, 2014: 1-5

7 T. L. Narasimhan, A. Chockalingam. Channel Hardening-Exploiting Message Passing (CHEMP)Receiver in Largescale MIMO Systems[J].IEEE Journal of Selected Topics in Signal Processing,2014, 8(5): 847-860

8 K. V. Vardhan, S. K. Mohammed, A. Chockalingam, etal. A Low-complexity Detector for Large MIMO Systems and Multicarrier CDMA Systems[J].IEEE Journal on Selected Areas in Communications,2008, 26(3): 473-485

9 P. Li, R. D. Murch. Multiple Output Selection-LAS Algorithm in Large MIMO Systems[J]. IEEE Communications Letters, 2010, 14(5): 399-401

10 B. S. Rajan, S. K. Mohammed, A. Chockalingam, etal. Lowcomplexity Near-ML Decoding of Large Non-orthogonal STBCs Using Reactive Tabu Search[C].The 2009 IEEE International Symposium on Information Theory, Seoul: IEEE Press, 2009: 1993-1997

11 P. Som, T. Datta, N. Srinidhi, et al. Low-complexity Detectionin Large-dimension MIMO-ISI Channels Using Graphical Models[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(8): 1497-1511

12 T. Datta, N. Srinidhi, A. Chockalingam, et al. A Hybrid RTS-BP Algorithm for Improved Detection of Large-MIMO M-QAM Signals[C].The 2011 IEEE National Conference on Communications,Bangalore: IEEE Press, 2011: 1-5

13 W. Fukuda, T. Abiko, T. Nishimura, et al. Complexity Reduction for Signal Detection Based on Belief Propagation in a Massive MIMO System[C].The 2013 IEEE International Symposium on Intelligent Signal Processing and Communications Systems,Naha: IEEE Press, 2013: 245-250

14 T. Datta, N. A. Kumar, A. Chockalingam. A Novel Montecarlo-sampling-based Receiver for Largescale Uplink Multiuser MIMO Systems[J]. IEEE Transactions on Vehicular Technology, 2013, 64(7):3019-3038

15 B. M. Hochwald, T. L. Marzetta, and V. Tarokh.Multipleantenna channel hardening and its implications for rate feedback and scheduling[J]. IEEE Trans. Inf. Theory, vol. 50, no. 9, pp. 1893–1909, Sep.2004

16 D. Tse and P. Viswanath, Fundamentals of wireless communication.Cambridge, U.K.: Cambridge Univ. Press, 2005

17 F. Rusek, D. Persson, B. K. Lau, E. G. Larsson, T. L. Marzetta,O. Edfors, and F. Tufvesson[J]. Scaling up MIMO: Opportunities and challenges with very large arrays IEEE Signal Process. Mag., vol. 30,no. 1, pp. 40–60, Jan. 2013

18 C. Studer, S. Fateh, and D. Seethaler.ASIC implementation of soft-input soft-output MIMO detection using MMSE parallel interference cancellation[J].IEEE JSSC,vol. 46, no. 7, pp. 1754–1765, July 2011

19 LU Lu, G. Y. Li, A. L. Swindlehurst, et al. An Overview of Massive MIMO: Benefts and Challenges[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 742-758

20 L. Dai, Z. Wang, and Z. Yang.Spectrally efficient timefrequency training OFDM for mobile large-scale MIMO systems[J]. IEEE J. Sel.Areas Commun., vol. 31, no. 2, pp. 251–263, Feb. 2013

21 F. Fernandes, A. E. Ashikhmin, and T. L. Marzetta.Inter-cell interference in noncooperative TDD large scale antenna systems[J].IEEE J. Sel.Areas Commun., vol. 31, no. 2, pp. 192–201, Feb. 2013

22 T. Uricar and J. Sykora.Non-uniform 2-slot constellations for bidirectional relaying in fading channels[J].IEEE Commun. Lett., vol. 15, no. 8,pp. 795–797, Aug. 2011

23 L. Chen.Iterative soft decoding of Reed-Solomon convolutional concatenated codes[J].IEEE Trans. Commun., vol. 11, no. 10, pp. 4076–4085,Oct. 2013

24 T. L. Marzetta.Noncooperative cellular wireless with unlimited numbers of base station antennas[J]. IEEE Trans. Wireless Commun., vol. 9,no. 11, pp. 3590–3600, Nov. 2010

25 H. Huh, G. Caire, H. C. Papadopoulos, and S. A. Ramprashad.Achieving “massive MIMO” spectral effciency with a not-so-large number of antennas[J]. IEEE Trans. Wireless Commun., vol. 11, no. 9,pp. 3266–3239, Sep. 2012

26 N. Srinidhi, T. Datta, A. Chockalingam, and B. S. Rajan. Layered tabu search algorithm for large-MIMO detection and a lower bound on ML performance[J]. IEEE Trans. Commun., vol. 59, no. 11, pp. 2955–2963,Nov. 2011

27 J. Goldberger and A. Leshem.MIMO detection for high-order QAM based on a Gaussian tree approximation[J]. IEEE Trans. Inf. Theory,vol. 57, no. 8, pp. 4973–4982, Aug. 2011

28 D. Argas, D. Gozalvez, D. Gomez-Barquero, and N. Cardona.MIMO for DVB-NGH, the next generation mobile TV broadcasting[J]. IEEE Commun. Mag., vol. 51, no. 7, pp. 130–137, Jul. 2013

29 H. Ngo, E. Larsson, and T. Marzetta.Energy and spectral efficiency of very large multiuser MIMO systems[J].IEEE Trans. Commun., vol. 61,no. 4, pp. 1436–1449, Apr. 2012

30 Y.-H. Nam, B. L. Ng, K. Sayana, Y. Li, J. Zhang, Y. Kim, and J.Lee.Full-dimension MIMO (FD-MIMO) for next generation cellular technology[J]. IEEE Commun. Mag., vol. 51, no. 6, pp. 172–179, Jun.2013

31 Jeffrey G. Andrews, Fellow, IEEE, Stefano Buzzi, Senior Member, IEEE, Wan Choi, Senior Member, IEEE, Stephen V. Hanly, Member, IEEE, Angel Lozano, Fellow, IEEE, Anthony C. K. Soong, Fellow, IEEE, and Jianzhong Charlie Zhang, Senior Member, IEEE. What Will 5G Be?[J]. IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, VOL. 32, NO. 6, JUNE 2014

2016-11-15）

10.3969/j.issn.1006-6403.2016.12.015