浅谈内地高中西藏生数学运算能力的培养策略

2017-01-12张瑞周伯明冯刚狄闻于

西藏教育 2016年12期

◆张瑞周伯明冯刚狄闻于

◆张瑞周伯明冯刚狄闻于

《普通高中数学课程标准（实验）》指出“高中数学课程应注重提高学生的数学思维能力，这是数学教育的基本目标之一。人们在学习数学和运用数学解决问题时，不断地经历直观感知、观察发现、归纳类比、空间想像、抽象概括、符号表示、运算求解、数据处理、演绎证明、反思与建构等思维过程。”［1］数学运算能力是数学三大能力之一，数学运算能力直接决定了学生的数学水平，是学生最基本的数学素养之一，所以，数学教师必须注重培养学生的数学运算能力。［2］目前我国关于对于内地西藏生这一特殊群体的数学运算能力的研究是寥寥无几的。在经过长期的教学实践探索和改革后，我校西藏生的成绩相对于前几届学生有了明显的提高，然而相对于我校的汉族学生，大部分学生的数学基础仍然是薄弱的，数学学习成绩是落后的，很多内地西藏高中生对数学的学习产生了畏难的情绪。为此，笔者尝试剖析内地西藏生的运算能力现状，探索出培养内地西藏生数学运算能力的培养策略。

一、调查研究

为调查研究内地西藏高中生的数学运算能力，了解他们的学习困难所在，笔者对我校高一两个西藏班的其中一个班级（共40人）做了实验调查，主要从学生解题错因分析，定期访谈学生，教学案例分析进行了具体的、有针对性的研究。

1.实验调查

笔者从实验班级的作业情况开始研究，对实验班的作业进行定量布置，每次10道题目，在评讲之后，要求学生对错题进行错因分析，错因主要包括审题不清、概率混淆、公式记错、计算失误、方法不当、毫无头绪等六大类，每个月统计一次，为期四个月。

表1 错因统计表

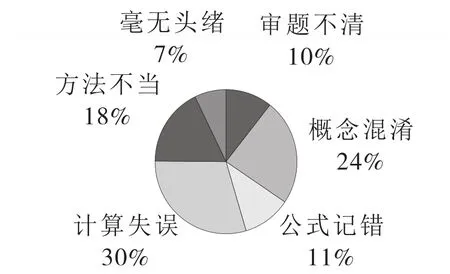
图1 合计错因分析饼状图

表1和图1表明内地西藏生的运算能力不足主要是由计算失误和概念混淆造成的，占整个错因的54%，同时定义、公式、法则、定理的运用能力，运算方法的选择能力都是数学运算能力的重要组成部分，审题能力直接影响着学生的数学运算能力，

2.定期访谈

为了访谈的公平性，笔者通过随机数表法对实验班进行了抽样访谈，每周一次访谈，每次访谈4人。访谈内容固定为：本周数学学习的困惑有哪些？结合具体的例子谈谈？你是如何理解本周所学习的几个数学概念、公式、定理的？经过长期的访谈记录，结果表明内地西藏高中生在数学学习上最大的问题是遗忘，上课能够理解的数学知识到了晚上作业时间就会有遗忘，复习时只能机械地去记忆，记忆效果不佳。对具体的数学问题习惯于套用老师课堂上讲解的例题，缺乏主动思考，这也会导致学生在进行数学运算时不够灵活。

3.教学案例

案例1：分式不等式的求解

对于分式不等式的解法，通过例题教学总结出解分式不等式的一般方法：移项、通分、化简。具体来说是将不等式一边化为0，通分，再将不等式等价地转化为二次不等式或者高次不等式求解。当学生在解不等式时，有的同学解出答案是x≥1，或这是由于未等价变形导致的，也就是说学生忽视了隐含条件“分母不为0”，经过多次练习，大部分同学能够掌握这类分式不等式的求解。但在求解不等式lg(x+2)-lg(x+1)〉1时，大部分学生会将不等式化为所以移项通分化简得解得而对于运算能力强的学生，会发现这里的隐含条件“真数部分大于0”，从而有解得

案例1表明，内地西藏生对数学题目信息的隐含条件的挖掘能力不足，容易局限于某个具体的解法口诀，盲目套用，缺乏主动思考和探索精神。

案例2：基本不等式

案例2表明，部分内地西藏生在对数学公式的记忆过于机械，当只是字母发生改变时就容易模糊，事实上，很多学生在初中运用求根公式求解一元二次方程时也常出现这样的问题，如一元二次方程2x2+x-2=0求解，学生会令a=2，b=1，c=-2，然后代入到学生所记忆的求根公式中，当把方程变为2x2+cx-2c=0时，学生就糊涂了。

案例3：圆的方程

圆的方程中有这样一个问题：若x,y满足方程x2+y2=4，求的最大值。学生很容易理解表示圆x2+y2=4点到定点(6,8)的距离，而且会结合图象解出正确答案。若将题目变式为求的最小值，学生能意识到将问题转化为两点间距离来求解，但是很难找到正确的方法，有学生将变形为学生会问自己为什么不好算呢？这显然是由机械模仿造成的，简单的模仿未能找到正确的途径，应该变形为其表示点(x,0)到两个定点(2,2)和(8,3)的距离之和。

案例3表明，学生对两点间距离公式掌握了，但是对具体情境的问题不能具体分析，只是由于曾经做过一道类似题目而去死套题型，不能优化运算方案。

二、培养策略

关于数学运算能力的培养策略已经有了很多的研究。李伯春等人认为培养学生的运算能力有三个途径：牢固掌握基础知识，弄通算理、法则；提高记忆能力，加强运算的基本功训练；加强运算练习，培养运算能力。［2］笔者结合内地西藏高中生的学习特点，探索一套适合培养西藏生的运算能力的策略。

1.加强数学概念的教学

数学知识几乎都是由概念组成，概念是数学思维的基础、最小单元，对数学概念的理解是提高学生对数学的认识，提高数学思维能力，解决数学问题能力的最好途径。学生在选择解题方案时必然要运用到相应的数学概念、公式、定理、法则等，学生只有对数学概念理解透彻和牢固掌握了才能准确、熟练地掌握好各种运算技巧，弄清算理和运算规则，否则一切都是无源之水无本之木。内地西藏班学生并没有内地汉族班学生的学习压力大，教师在教学时更应该注重以生为本，把课堂还给学生，创设适当的教学情境和教学活动，引导学生积极主动地参与到课堂中来，让学生在数学活动中感悟和理解数学概念，当数学的概念是由学生自己通过努力而获得的时候学生就不容易遗忘了。如集合的教学时，应当通过大量的身边的实例来帮助学生理解集合的元素所满足的确定性、无序性和互异性，而集合本身又是一个描述性的概念，教师不可以把书本上对集合的描述性概念拿出来让学生背诵，否则学生将高中起始就陷入到机械记忆的地步，今后的数学运算能力的发展就会受到制约。

2.加强数学公式理解和记忆的指导

数学运算大多数会涉及到数学的公式计算，公式遗忘或者混淆是内地西藏生在进行公式计算时遇到的最大问题，因此在学习一个数学公式时教师要指导学生记忆和理解公式。如两角和差的余弦公式cos(α±β)=cosαcosβ∓sinαsinβ，课堂引入时不易同课本那样运用向量的数量积来引入，原因是过于抽象，不利于大部分西藏生接受，更好的方法是编制简单易懂、学生感兴趣的问题（如小明认为cos15°=cos(45°-30°)=cos45°-cos30°，你同意小明的做法吗？）引入课堂，学生获得公式之后可以给出公式记忆口诀“余余正正，和差相反”学生理解了两角和差的余弦公式了，对后续学习两角和差的正弦、正余弦的二倍角公式都有正迁移的作用，即使今后忘记了这些公式，学生也能自己推导出来。对于公式计算，我们应当要求学生列出公式再计算，如求两点A(1,-1)，B(-2,3)间的距离。应当要求学生根据两点间的距离公式，列出式子再计算，即这样的公式计算应当避免跳步计算，保证算正确。

3.加大运算教学力度

对于内地西藏高中班学生的运算能力的培养应到被教师提到教学议程上来，有计划有目的地培养，加强运算训练，做好教学示范。首先要强调运算结果的美观性和实用性指导，以美激趣，以善动人，如直线方程x+y-1=0不应该写成y+x+1=0，这就像人每天起床后需要化妆一样，追求美观，再如一元二次方程的求根公式这显然是一个没有什么美观可言的公式，但它可以帮助我们解决任何一个有解的一元二次方程的根，作用之大令人叹服，因此教师要围绕提高学生运算兴趣做文章；其次可以开展提高运算能力的游戏、活动，如在班级开展数学计算竞赛，培养兴趣小组；再者重视培养学生良好的计算习惯，教师一要做好审题示范和计算示范，二要对学生的作业提出具体计算要求，养成打草稿、规范书写、检验结果的好习惯。