多激励宽带复合棒换能器设计

胡负稷, 张文波, 王明洲



多激励宽带复合棒换能器设计

胡负稷1,2, 张文波1, 王明洲1,2

(1. 中国船舶重工集团公司第705研究所, 陕西西安, 710077; 2. 水下信息与控制重点实验室, 陕西西安, 710077)

多谐振宽带复合棒换能器因采取耦合多个振动模态的方式, 在拓宽频带方面取得了很好的效果而被广泛使用。为进一步适应水声信号技术的发展要求, 文中采用等效电路法和有限元分析法对前盖板弯曲振动的双激励源多谐振换能器性能进行了对比分析, 2种方法所得结论吻合较好。最后采用ANSYS有限元分析软件对三激励源多谐振换能器进行了研究。结果表明, 双激励多谐振换能器的带宽得到有效拓宽, 三激励源多谐振换能器在工作频带内受质量块厚度的影响较小。文中工作可为多谐振宽带换能器带宽和起伏的设计提供参考。

水声信号; 宽带复合棒换能器; 双激励; 三激励; 多谐振

0 引言

水声换能器作为水声通信的核心部件之一, 一直是水声领域研究的重点。随着水声通信技术的不断发展, 水声换能器的性能要求也随之提高。带宽作为水声换能器的一项重要性能指标, 一直是换能器研究人员不断尝试研究突破的内容。宽带换能器在信号传输中能保持信号的完整性和准确性, 其较大的带宽还可以实现多频通信。因为这些优势, 宽带换能器在鱼雷制导、声诱饵投放、超声医疗和超声探伤等方面被广泛应用。

多谐振宽带换能器研究近年来也取得了很大的成果, 有纵弯耦合、加入柔顺层或匹配层、双激励、单端激励等方法[1], 但这些方法设计出的换能器带宽大部分只达20 kHz左右, 又或者发送电压响应(transmitting voltage response, TVR)的起伏较大[3-6]。文中将基于此进一步研究多谐振宽带换能器, 以期得到更宽的带宽, 针对现阶段研究较少的三激励源多谐振换能器也进行了一些初步研究。

1 多激励宽带换能器设计

多谐振宽带换能器工作的基本原理就是使工作频段内的多个振动模态相互耦合, 因此, 多谐振宽带换能器的带宽相较于传统复合棒换能器有较大拓宽。图1为多模振动耦合的实现原理, 图中,为各谐振频率。在设计多谐振宽带换能器时需要注意各谐振频率的间隔, 避免发送TVR曲线产生较大凹谷, 一般来说两相邻谐振峰的间隔不能超过30 kHz。

1.1 双激励源宽带换能器

1.1.1 等效电路分析

首先根据机电等效原理来分析双激励源宽带换能器的谐振频率, 双激励源换能器的等效电路图如图2所示。图中, 各虚线框内的元件分别等效为,,和。

图2中的电路可以使用四端网络的并联来求解, 其中2个四端网络最终可以等效为1个四端网络, 该网络右端与图2中连接[7-8], 设这个四端网络的导纳参数为, 则总的阻抗表达式为

对于双激励源换能器, 可将其等效为2个简单的复合棒换能器进行分析。将图2中的、和一个支路去掉即为普通复合棒换能器的等效电路图, 设

(2)

则其阻抗表达式为

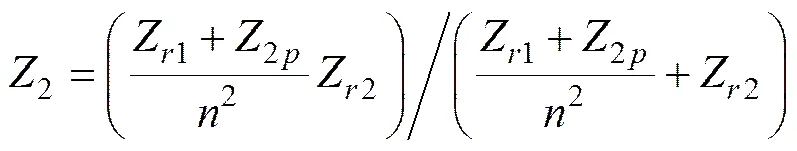
根据导纳与阻抗的关系

(4)

可求出换能器的谐振频率。

文中研究的双激励源换能器模型参数为: 陶瓷片材料PZT-4, 半径8 mm, 前晶堆包含4片陶瓷, 后晶堆包含2片陶瓷; 前盖板材料为硬铝, 半径18 mm; 中间质量块材料为黄铜, 厚度6 mm; 后盖板材料为黄铜, 厚度15 mm。

根据上述参数, 使用式(1)得出的谐振频率分别为25 kHz和43 kHz, 使用式(2)得出的谐振频率分别为17 kHz和58 kHz。

1.1.2 有限元仿真分析

为了进一步验证等效电路法所得的结论, 下面使用ANSYS软件进行有限元仿真分析换能器模型。所使用的有限元方程为

在ANSYS软件中经过建立换能器的模型, 添加材料参数及赋属性、分网、施加载荷、求解等步骤求得的导纳曲线如图3所示。从图中可知, 该换能器的谐振频率分别为24 kHz和52 kHz。

表1为图3的谐振频率和等效电路法结果对比。

表1 等效电路法和有限元法计算的谐振频率

从表1中可以发现, 由式(1)所得的第1阶谐振频率与有限元法所得结果比较吻合, 式(3)所得的高阶谐振频率则更接近有限元仿真结果。实际上, 因为有弯曲振动的影响, 这样理想的等效电路法是不够准确的, 但在换能器初始设计时可以提供一定的参考。

对于图3中46 kHz附近出现的起伏, 可以用换能器前盖板的弯曲振动来解释。圆盘的弯曲振动横向位移可以表示为

(7)

式(7)的解有无数多个, 分别对应着圆盘振动的各阶频率, 设各阶解为, 得到圆盘各阶频率的解

1.1.3 双激励换能器质量块对TVR的影响

使用ANSYS求解TVR时, 需要考虑水对换能器的影响, 一般将水等效为1个水球, 再加载荷, 求解即可[7], 换能器在水中的模型见图4。

根据发送电压响应级的计算公式

在ANSYS中提取声轴线上节点声压, 进行相应的运算即可求出换能器的TVR曲线, 其中为节点到声源等效中心的距离,为施加的电压。设前盖板厚度为, 中间质量块厚度, 后盖板厚度, 针对不同的质量块厚度分别使用ANSYS仿真计算其TVR曲线, 结果如图5所示。

图5 双激励换能器各质量块厚度对发送电压响应的影响

Fig. 5 Effects of mass thickness of on transmitting voltage response(TVR)

1.2 三激励源宽带换能器

在上节中的双激励源换能器已出现了3个谐振峰, 在本节中尝试设计三激励源的宽带换能器, 以提高宽带换能器的性能。在设计三激励源宽带换能器时可以参考双激励源宽带换能器模型, 在这里对上节的模型进行适当变换, 在前晶堆中间插入黄铜质量块(其厚度为)使其变成一个具备3个激励源的换能器模型。使用ANSYS计算出不同的质量块厚度对TVR曲线的影响如图6所示。

从图6可以看出, 前晶堆插入的质量块没有产生新的谐振点, 但插入的质量块只对第2阶谐振峰产生了较大的影响, 使第2阶谐振频率下降很大, 第2阶和第3阶谐振峰之间的凹谷也随着的增加急剧下凹, 这是在设计换能器时需要多加注意的地方。如果需要单独调节第2谐振峰的话, 在前晶堆中插入质量块是一种可以考虑的方法。

2 结束语

文中采用多模态耦合的方法进一步拓宽了多谐振宽带换能器的工作带宽, 运用等效电路法和ANSYS软件分析了换能器的谐振频率, 针对质量块厚度这一影响TVR曲线的主要因素进行了仿真分析。

仿真结果表明, 对于双激励源换能器, 增加质量块的厚度能有效减小各谐振峰间的间隔, 后盖板厚度的增加能有效降低换能器各谐振频率, 各质量块厚度对后2阶谐振频率都有非常明显的影响。对于三激励源换能器, 新插入的质量块能够单独调节第2谐振峰。文中研究可以为多谐振宽带换能器带宽和起伏设计提供参考。

[1] 徐钧, 俞宏沛, 李建成. 纵振换能器拓宽频带的方法综

[2] 述[J]. 声学与电子工程, 2003(4): 17-21.

[3] Qing S Y, Leif B. Broadband Tonpilz Underwater Acoustic Transducers Based on Multimode Optimization[J]. IEEE, 1997, 44(5): 1060-1066.

[4] 俞宏沛, 潘先松, 赵颂阳, 等. 双激励源振子的初步理论分析与实验研究[J]. 声学与电子工程, 1997(4): 24-27.

[5] 张文波, 王明洲, 郝保安. 双激励宽带水声换能器理论研究[J]. 鱼雷技术, 2007, 15(2): 34-37.Zhang Wen-bo, Wang Ming-zhou, Hao Bao-an. Theoretical Study on Broadband Underwater Transducer with Do- uble Resonant Mode[J]. Torpedo Technology, 2007, 15(2): 34-37.

[6] 林书玉. 纵向振子与圆盘组成的弯曲振动超声换能器的研究[J]. 声学与电子工程, 1993(3): 21-25.

[7] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 第3版. 南京: 南京大学出版社, 2012.

[8] 莫喜平. ANSYS软件在模拟分析声学换能器中的应用[J]. 声学技术, 2007, 26(6): 1279-1290.Mo Xi-ping. Simulation and Analysis of Acoustics Trans- ducers Using the ANSYS Software[J]. Technical Acoustics, 2007, 26(6): 1279-1290.

[9] 李志强, 李英明莫喜平等. 双激励压电复合棒换能器中间质量块研究[J]. 声学技术, 2013, 32(6): 273-274. Li Zhi-qiang, Li Ying-ming, Mo Xi-ping, et al. Research of the Massstuck in the Piezoelectric Ceramic Stack of Tonpilz Transducer with Double Excitation[J]. Technical Acoustics, 2013, 32(6): 273-274.

[10] 李建成, 李红敏. 双谐振柔顺层换能器[J]. 声学与电子工程, 2011(2): 33-36.

[11] 孙好广, 余宏沛, 欧阳哲. 双激励宽带换能器的有限元设计[J]. 声学与电子工程, 2003(3): 12-14.

[12] 赵双, 董铭锋, 唐义政. 匹配层三谐振宽带换能器设计[J]. 声学与电子工程, 2015(3): 17-19.

(责任编辑: 杨力军)

Design on Multi-excitation Broadband Tonpilz Transducer

HU Fu-ji,ZHANG Wen-bo,WANG Ming-zhou

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710077, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710077, China)

Multi-resonant broadband Tonpilz transducer takes the way of coupling multiple vibration modes, so it broadens frequency band. In this paper, for the development of underwater acoustic signal technology, the equivalent circuit method and the finite element analysis method are used to analyze the performance of the double-excitation source multi-resonant transducer for bending vibration of the front cover plate. The results of these two methods are in good agreement. Moreover, the finite element analysis software ANSYS is employed to investigate triple-excitation source multi-resonant transducer. The results show that the frequency band of the double-excitation source multi-resonant transducer is effectively broadened, and the triple-excitation source multi-resonant transducer undergoes small influence of the mass thickness in its working frequency band. This study may provide reference for design of bandwidth and fluctuation of the multi-resonant broadband transducer.

acoustic signal; broadband Tonpilz transducer; double-excitation; triple-excitation; multi-resonant

10.11993/j.issn.1673-1948.2016.06.005

TJ630.34; TB565.1

A

1673-1948(2016)06-0422-04

2016-08-12;

2016-10-22.

胡负稷(1990-), 在读硕士, 主要研究方向为水声换能器与声系统技术.