U型65Mn钢板限位器扭转性能研究
2017-01-12冯红达杜红凯
韩 淼, 冯红达, 杜红凯
(北京建筑大学 土木与交通工程学院,北京 100044)
U型65Mn钢板限位器扭转性能研究
韩 淼, 冯红达, 杜红凯
(北京建筑大学 土木与交通工程学院,北京 100044)
通过对U型65Mn钢板限位器的扭转性能研究,推导其弹性扭转刚度及屈服荷载的理论计算公式,给出公式的适用范围. 设计制作平直段长度L、宽度b、及钢板厚度t不同的40种限位器,进行静力加载试验. 结果表明,限位器扭转位移主要由圆弧段扭转引起,钢板厚度t对限位器扭转刚度影响最大,增加板厚能够有效地增大刚度;板宽与刚度K近似呈一次正比关系;平直段长度越大,限位器扭转刚度越小. 利用实验数据对理论公式进行修正,得到公式的修正系数. 修正后的理论公式与实验数据吻合较好.
限位器; U型钢; 扭转性能; 理论公式; 静力试验
对于常规地震,基础隔震能够延长结构的自振周期,避开地震动卓越周期,减小上部结构地震反应. 但是对于近断层和长周期地震,隔震支座可能产生较大变形,导致结构失稳或支座破坏. 对此韩淼等[1]提出增加缓冲限位装置作为第二道防线. U型65Mn钢板限位器具有一定的自复位能力,且取材容易,结构简单,造价便宜. 韩淼、杜红凯等[2-6]对U型65Mn钢板限位器的平面内性能进行了理论分析和试验研究,提出了刚度的理论计算公式.
由于地震发生时方向的不确定性,上部结构可能会在任意方向与限位器发生碰撞,限位器不可避免地会发生一定程度的扭转变形(如图1所示). 为完善限位理论,本文将进一步对限位器的扭转性能开展理论及实验研究.
1 限位器扭转力学性能修正系数
限位器构造示意图如图2所示,主要设计参数包括平直段长度L,平直段宽度b,圆弧段半径R,钢板厚度t.
为推导限位器扭转刚度的计算公式,做出如下假设:
1) 平直段端部的扭转位移D全部由圆弧段的扭转引起,扭转力臂为L+R,扭转角为φ. 图3给出了限位器扭转恢复力的计算简图.
2) 把圆弧段的扭转等效为b×t的等截面矩形截面直杆的扭转,杆长l=2R(如图4所示).
根据矩形截面杆件弹性理论计算公式,等截面矩形杆件的扭转角φ为:
(1)
其中,T为扭矩;l为等效矩形等截面杆件长度,取l=2R;G为剪切模量,取为0.4E[7];β为矩形截面杆扭转时的系数(表1所示);b和t分别为矩形截面的长度和宽度.

表1 矩形截面杆扭转时的系数β[8]361
U型钢板扭转刚度:
(2)
其中:F为扭转弹性恢复力;D为平直段端部扭转位移.
(3)
D=(R+L)φ
(4)
式(1)、式 (3)、式(4)代入式(2)得到:
(5)
式(5)即为限位器扭转刚度计算公式.
根据弹性理论,图4中等效矩形直杆发生扭转时,最大切应力τmax发生在矩形长边中点,即:
(6)
τmax=Gεy
(7)
其中α为矩形截面扭转时的系数(表2所示).εy为U型65Mn钢的屈服应变.

表2 矩形截面杆扭转时的系数α[8]362
式(6)、式(7)代入式(1),得到:
(8)
当b/t≥5时,α=β,此时公式(8)可简化为:
(9)
式(8)即为屈服扭转角的计算公式.
由式(2)、式(4)、式(5)、式(8)可得以应变εy表达的屈服荷载F′的计算公式:
(10)
式(5)、式(10)为限位器扭转刚度与荷载的理论公式. 为使公式计算结果与工程实际相符,对公式做出如下修正:
(11)
(12)
式(11)、式(12)中的ω、η为弹性刚度与屈服荷载的修正系数.
该公式表明,厚度t与半径R对刚度的影响最大,增加厚度或者减小半径能够有效地增大刚度;同时增加板宽b或者减小平直段长度L也可增加刚度K. 屈服荷载受板厚t的影响最大,与板厚t呈二次方关系,另外增加板宽b或者减小半径R和平直段长度L也可增大屈服荷载.
2 约束U型钢板扭转力学性能试验
2.1 材料性能
在万能试验机上对不同厚度的钢板标准件进行拉伸试验,数据分析表明此类钢板没有明显的流幅段,达到极限强度时会脆断. 图5为典型65Mn钢应力- 应变曲线,表3列出了各种厚度钢板的屈服强度fy、极限强度fu及屈服应变εy的实测值.
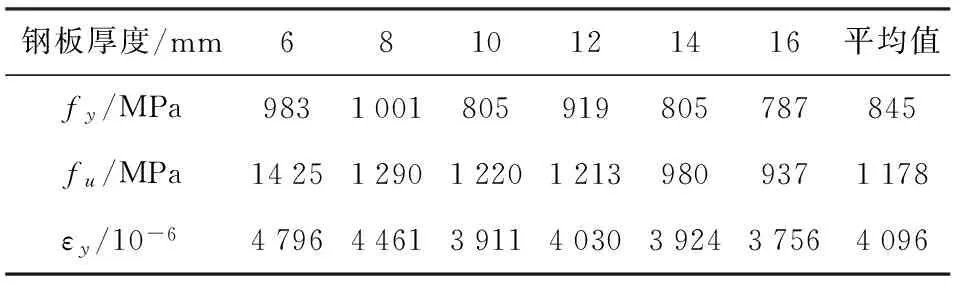
表3 各种厚度钢板的屈服强度fy、极限强度fu、屈服应变εy
2.2 试验概况
本试验在北京建筑大学结构实验室完成,采用MTS25t作动器. 实验装置示意图如图6所示. 采用伺服作动器施加水平力,千斤顶提供的水平推拉力通过加载板传递给U型限位器,限位器通过螺栓与固定板连接,加载板与底座之间放置滚轴以减小两者之间的摩擦力. 为防止U型钢发生侧向移动,每次试验采用两个U型钢对口对称布置,如图7所示.U型钢试件实物图如图8所示.
为研究限位器在水平推力作用下扭转的力学性能,根据平直段长度L、宽度b,钢板厚度t三种不同设计参数,采用65Mn钢设计制作了40种不同规格的U型钢板限位器,表4给出了40种限位器的设计参数.
对试件进行四次低周往复推拉试验,推拉位移幅值分别为10mm、25mm、50mm、100mm. 图9给出了试件U1的荷载- 位移滞回曲线(U2-U40与其类似,篇幅限制不再列出),结果表明:在位移幅值为R(100mm)范围内限位器保持弹性. 图10给出

表4 试件参数表
刚度K与厚度t3的关系曲线,图11给出了刚度K与宽度b的关系曲线. 结果表明:刚度K与t3、b均呈正比关系. 图10中b=40;L=150与b=40;L=200两条曲线表明:减小L可以增大刚度K.
3 对理论公式的修正
图9可知,加载过程中限位器均保持线弹性,取限位器加载时滞回曲线的斜率作为其弹性扭转刚度,表5给出了限位器扭转刚度的实验值. 由公式5计算得到限位器扭转刚度的计算值,按照40组限位器的计算值与实验值的平均偏差为零对公式5进行修正,得到修正系数ω=1.328 9. 此修正系数95%的置信区间为(1.064 6,1.809 8). 加载量程限制,推拉位移幅值为100 mm,所有试件均未屈服,可知修正后屈服荷载的计算值不应小于试验位移幅值d=100 mm时的推力值F,推知η≥5.291 1.

表5 弹性扭转刚度表
表6给出了U1- U40修正后计算刚度与实验刚度对比结果,由表可知,吻合较好.
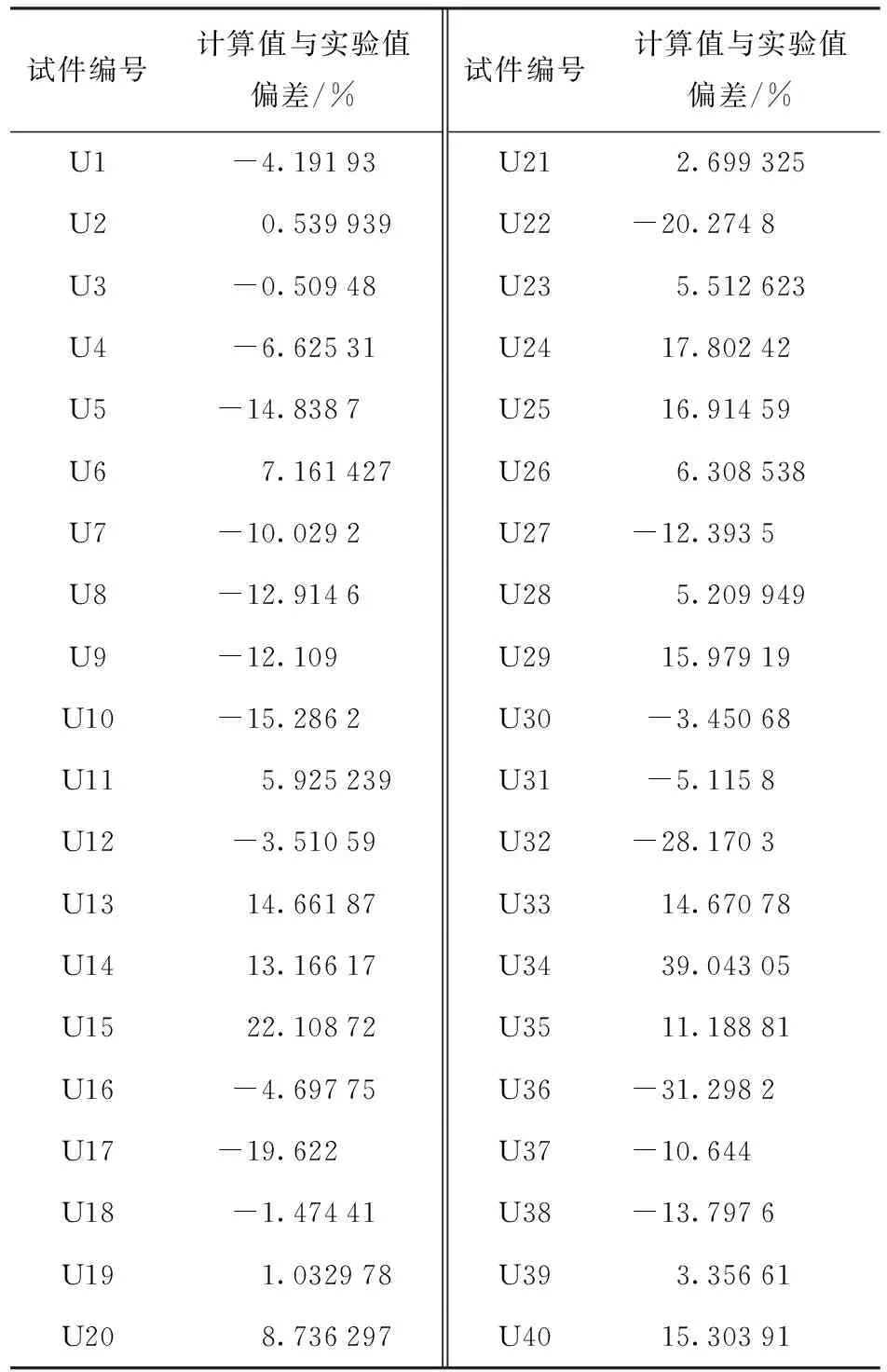
表6 修正后计算值与实验值偏差
4 结论
设计制作40种U型65Mn钢板限位器,进行力学性能试验,给出扭转刚度、屈服荷载的计算公式,以及修正系数.
1) 限位器扭转刚度与t3呈正比,与b呈一次正比,并随平直段长度L的增大而减小.
2) 给出限位器扭转刚度计算公式,以及屈服荷载计算公式,对比实验数据对其进行修正,得到修正系数ω=1.328 9,η≥5.291 1.
3) 试件U1- U40位移- 荷载滞回曲线表明,在扭转位移幅值为R(100 mm)范围内,限位器保持弹性.
[1] 韩淼,周锡元.基础隔震建筑软碰撞保护分析[J].建筑科学,1999, 15(1): 14-20
[2] 韩淼,杜红凯,李仙华.基础隔震层软碰撞限位实验研究[J].工程力学,2008(S1):132-136
[3] 韩淼, 李仙华.U型组合限位器自复位性能实验研究[J].世界地震工程, 2006, 22(2): 110-113
[4] 杜红凯, 韩淼, 闫维明. 约束U 形钢板力学性能的计算方法研究[J]. 土木工程学报, 2014, 47(S2): 158-163
[5] 杜红凯, 韩淼, 闫维明. 约束U形钢板力学性能的计算方法研究[J]. 土木工程学报, 2014(s2):158-163
[6] 韩淼, 李仙华, 伍大维. 基础隔震建筑软碰撞耗能分析[C]. 全国地震工程学术会议,2006
[7] 崔相东, 杜红凯, 韩淼,等. U型65Mn钢板隔震限位器滞回性能试验研究[J]. 工程抗震与加固改造, 2015, 37(2):102-107
[8] 刘鸿文. 高等材料力学[M]. 北京: 高等教育出版社, 1985
[责任编辑:佟启巾]
Study on Torsional Behavior of 65Mn U Type Steel Plate Limiter
Han Miao, Feng Hongda, Du Hongkai
(School of Civil and Traffic Engineering, Beijing University of Civil Engineering and Architecture,Beijing 100044)
In this study, the torsional behavior of 65Mn U type plate limiter is studied; the theoretical calculation formula of elastic torsion stiffness and yield load are derived, and the applicable range of the formula is given. The 40 kinds of limit device with different flat plate length L, width b, and steel plate thickness t are carried out for static load test. The results show that the torsional displacement of limiter is mainly from the torsion of circular arc section. The thickness of the plate affects the maximum of torsional stiffness of the limiter, and the thickness of slab can effectively increase the stiffness; the width of plate and stiffness K is approximately a linear relationship; the larger the straight section length the smaller the torsional stiffness of the limiter. The theoretical formula is modified by the experimental data, and the correction coefficient of the formula is obtained. The modified theoretical formula is in good agreement with the experimental data.
limiter; U type steel; torsional behavior; theoretical calculation formula; static load test
2016-07-28
国家自然科学基金项目(51378047,51408027)
韩 淼(1969—),男,教授,博士生导师,博士,研究方向: 工程结构抗震减灾及抗震性能.
1004-6011(2016)04-0001-05
TU352.1+1
A
