改进的不等时距灰色马尔科夫模型在边坡位移预测中的应用
2017-01-11谢金华厦门大学建筑与土木工程学院福建厦门361005厦门大学嘉庚学院福建漳州363105厦门大学深圳研究院广东深圳518057
胡 华,谢金华(1.厦门大学 建筑与土木工程学院, 福建 厦门 361005,2.厦门大学 嘉庚学院, 福建 漳州 363105; 3.厦门大学 深圳研究院, 广东 深圳 518057)
改进的不等时距灰色马尔科夫模型在边坡位移预测中的应用
胡 华1,2,3,谢金华1,2
(1.厦门大学 建筑与土木工程学院, 福建 厦门 361005,2.厦门大学 嘉庚学院, 福建 漳州 363105; 3.厦门大学 深圳研究院, 广东 深圳 518057)
研究了改进的不等时距灰色马尔科夫模型在边坡位移预测中的应用,先用S型函数对厦门某边坡的实测数据进行平滑处理,然后用平滑后的数据建立不等时距灰色GM(1,1)模型,最后用改进的计算公式求得马尔科夫模拟值和预测值。结果表明改进后的不等时距灰色马尔科夫GM(1,1)模型的拟合精度和预测精度有了很大的提高,对边坡稳定性预测有一定的参考价值。
灰色马尔科夫模型;边坡位移预测;S型函数
边坡是一个受到多种因素影响而发展演化成的非线性开放系统。边坡的演进和破坏具有随机性和不确定性,而边坡的位移变化携带了边坡破坏的重要信息,因此,对边坡内部位移监测数据进行分析,并建立相应的预测模型,对保证边坡安全、掌握岩土结构的形成、发展、未来的发展趋势及其变化规律具有十分重要的意义。现有的边坡位移监测资料分析方法很多,主要有多元回归分析方法[1]、BP神经网络分析方法[2]、时间序列分析方法[3]等,这些方法大都需要建立在大样本的基础之上,而边坡的位移变化往往受多种因素的影响,具有随机性和复杂性,这些方法很难对边坡的位移变化趋势做出可靠的预测。经研究发现,灰色系统理论非常适用于“小样本,贫信息”的预测,通过已有的数据信息来拟合反应数据行为特征的曲线,进而实现对未来行为的预测[4-5]。近年来,基于灰色系统模型的位移预测方法越来越引起人们的重视,被证明是一种很好的位移预测方法,但是当数据序列波动较大或者数据序列较长时,传统的灰色系统模型往往很难得到理想的预测结果。针对上述现象,有学者提出,先对数据序列进行平滑处理,然后再建模预测,并获得了良好的预测结果[6]。也有研究人员提出基于灰色系统的组合模型,如灰色BP神经网络模型[7]、灰色马尔科夫模型[8-12]等,其中灰色马尔科夫模型的提出使得灰色模型的预测精度有了很大的提高,但是传统的灰色马尔科夫模型不能满足预测精度的需要。因此,很多学者对灰色马尔科夫模型进行了改进[13-16],这使得灰色马尔科夫模型的预测精度有了进一步提高。
S型函数能够把数据序列压缩到(0,1)这个小区间内,使原始数据变得光滑,该文先用S型函数对厦门市金尚路的路基边坡实际监测水平位移数据序列进行平滑处理,然后再用平滑后的数据建立不等时距GM(1,1)模型,并采用新的公式计算马尔科夫模拟值,结果表明预测精度有了很大程度的提高,对边坡稳定性预测有一定的参考价值。
1 灰色系统GM(1,1)模型建模原理
灰色系统理论的主要观点是先对数据进行累加处理,建立数学模型,然后再进行预测。累加生成是灰色系统建模的一种常用生成方法,记作AGO,累加生成可以知晓数据积累过程的发展趋势。设原始离散数据序列:
x(0)=[x(0)(1),x(0)(2),……,x(0)(n)]
(1)
其中Δtk=tk-tk-1=1(k=1,2,……,n),对x(0)作一次累加生成得到新的数列:
x(1)=[x(1)(1),x(1)(2),……,x(1)(n)]
(2)
式(2)的元素
(3)
x(1)(tk)的时间响应表达式为:
(4)
其中a、u为待定参数,用最小二乘法就可以将参数a、u解出来。其中a叫做发展系数,反映增长趋势,u叫做灰作用量。
(5)
(6)
Y={x(0)(t2),x(0)(t3),…,x(0)(tn)}T
(7)
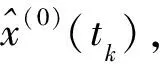
(8)
2 预测模型的改进和建模方法
2.1 改进不等时距GM(1,1)模型的建模原理
建模前,用S型函数对原监测数据进行光滑处理。S型函数的表达式为f(x)=1/(1+e-x)该函数能够把数据压缩到(0,1)这个小区间内,使原始数据变得光滑。用S型函数处理后的数据进行建模往往能够提高模型的预测精度。具体方法如下,设有一组不等时距监测数据序列:
x(0)=[x(0)(t1),x(0)(t2),…,x(0)(tn)]
(9)
其中,Δtk=tk-tk-1≠1(k=1,2,…,n),k为离散数据对应的时间。用S型函数处理后变为:
x(00)=[x(00)(t1),x(00)(t2),…,x(00)(tn)]
(10)
对光滑处理后的数据进行累加处理有:
x(01)(tk)=x(00)(t1)×Δt1+…+x(00)(tk)×Δtk
(11)
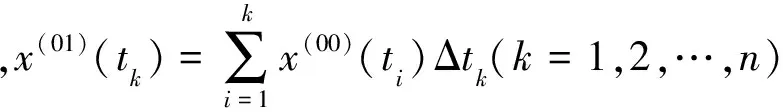
(12)
数据累减还原考虑时间因子Δtk后得到灰微分方程:
dx(01)(tk)/dt+αx(01)(tk)=u
(13)
求解灰微分方程就可以得到改进不等时距数列微分方程的时间响应公式:
(14)
(15)
2.2 不等时距GM(1,1)模型灰参数的求解
(16)
累加生成数据与模拟值之间应存在下列关系:
(17)
(18)
解方程可得:
(19)
(20)
(21)
(22)
其中,tk
2.3 改进马尔科夫预测模型的建模步骤
使用传统的公式计算得到的不等时距灰色马尔科夫模拟值和预测值的误差较大,该文将采用新的公式计算模拟值和预测值。
(1) 划分马尔科夫状态。结合边坡位移数据样本,根据相对残差的取值范围进行马尔科夫状态划分。
(2) 确定状态转移概率矩阵。状态转移矩阵里的每个元素的计算公式如下:Pij=Nij/Ni,其中Ni为状态i发生转移的次数,Nij为状态i转移到状态j出现的次数,Pij为状态i转移到状态j发生的概率。
(3) 改进马尔科夫模拟值的计算方法。由状态转移矩阵和各个模拟值所处的状态可以确定灰色马尔科夫模拟值。传统的马尔科夫模拟值的计算公式如下:
(24)
改进的计算公式如下:
(25)
其中:
3 改进的不等时距灰色马尔科夫GM(1,1)在边坡位移预测中的运用
以厦门市金尚路的路基边坡为例。本边坡工程大致为北西—南东走向,倾向北东,总体呈倒L形,长约142 m,坡高约6.7 m~9.0 m,边坡较陡,坡度约60°~75°。现场的7个沉降观测点及7个水平位移观测点布置在边坡顶上;35个沉降观测点布置在边坡坡顶的建筑物上。监测精度为1 mm。由于监测点众多,现在以CX3监测点2月28日以后的监测数据为依据,用S型函数进行光滑处理,然后进行建模和位移预测,以验证改进的不等时距灰色马尔科夫模型的准确性和其用于位移预测的有效性。监测数据见表1。

表1 CX3监测点的监测数据
3.1 建模过程及计算
3.1.1 初始位移序列
由表1可得到
x(0)={x(0)(t1),x(0)(t2),…x(0)(tn)}=
{3.45,3.50,3.60,3.75,3.80,3.90,3.90,3.90}
(26)
用S型函数处理后称为新的序列
x(00)=[x(00)(t1),x(00)(t2),…x(00)(tn)]=
[0.969231,0.970688,0.973403,0.977023,0.978119,
0.980160,0.980160,0.980160]
(27)
3.1.2 可行性判断
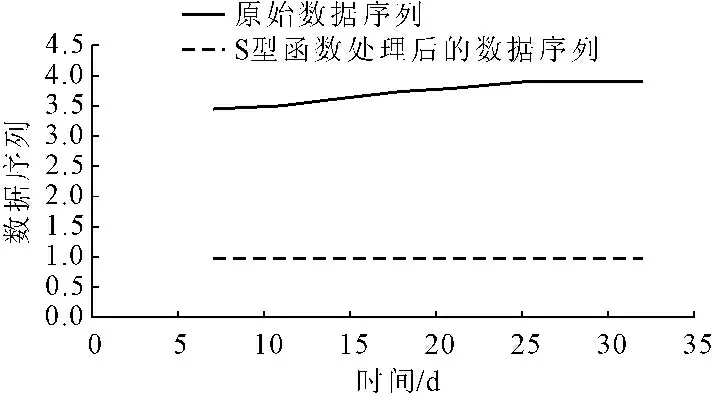
可以证明x(0)和x(00)都是准光滑序列,可以直接用初始数列进行建模。由下图1也可以看出x(00)序列趋近于一条直线,光滑度明显比x(0)的光滑度要高,同样也可以证明下式成立。
(28)
图1 光滑性对比图
3.1.3 累加生成数列
原始监测数据累加生成后的序列为
x(1)=[x(1)(1),x(1)(2),……,x(1)(n)]=[24.15,
38.15,48.95,63.95,75.35,90.95,102.65,118.25]
(29)
S型函数累加生成后的序列为:
x(01)=[x(01)(1),x(01)(2),……,x(01)(n)]=
[6.784617,10.667369,13.587578,17.495670,
20.430027,24.350667,27.291147,31.211787]
(30)
3.1.4 确定不等时距GM(1,1)模型方程
(31)
根据初始残差建立对应的残差模型如下:
(32)
最终的灰色GM(1,1)模型方程为:
(33)
(34)
累减还原后可以得到不等时距GM(1,1)模拟值,改进的不等时距模拟值与实际值对比见表2。
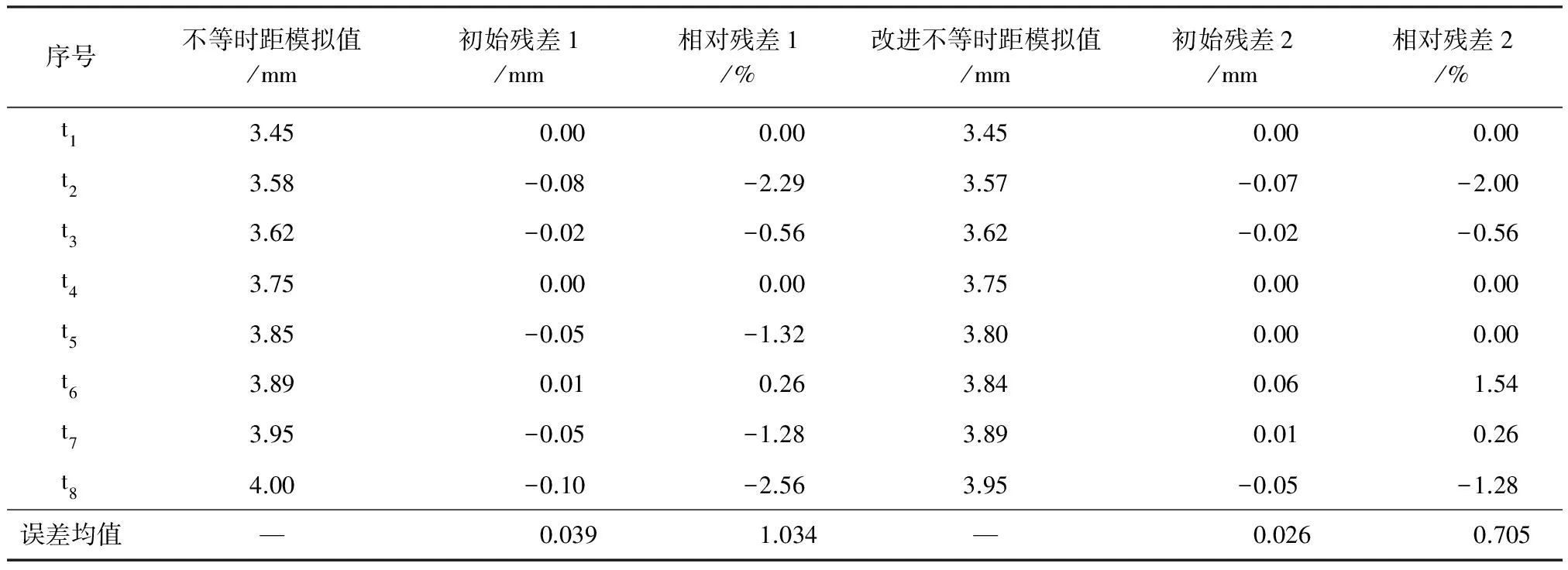
表2 模拟值与实际值比较
由表2可以计算出改进后的模型在原基础上均误差和相对均误差减小了33.33%和31.82%,可见用S函数平滑处理原始数据再建模能提高模型的模拟精度。
3.2 改进的灰色不等时距马尔科夫模型
3.2.1 划分马尔科夫状态
结合表2中的数据,根据相对残差的取值范围可以将CX3号监测点的马尔科夫状态划分为4个不同的状态,其划分情况见表3。
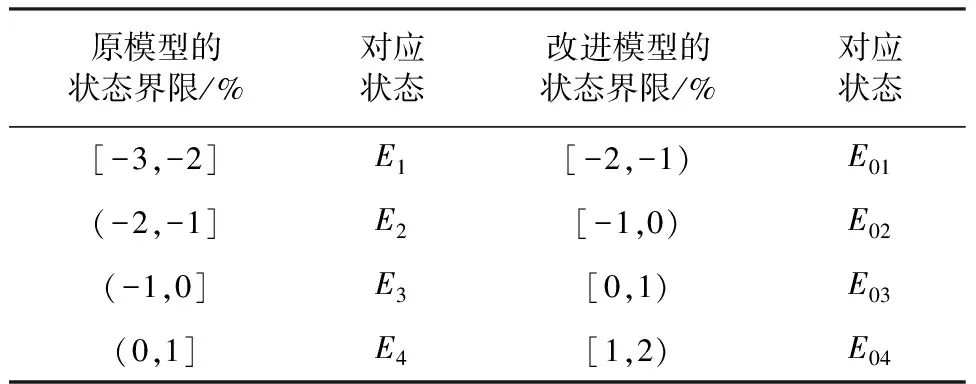
表3 状态划分
3.2.2 确定状态转移概率矩阵
根据公式Pij=Nij/Nj计算状态转移矩阵里的每个元素。求得原模型和改进模型的一步状态转移概率矩阵P(1)和P(01):
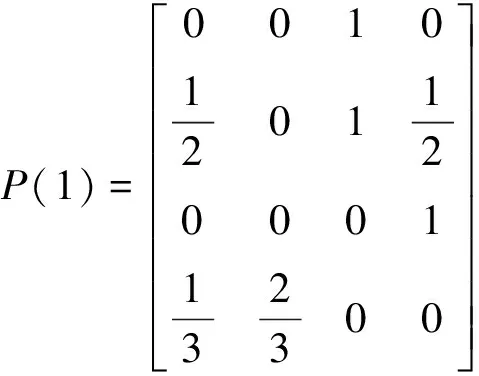
3.2.3 计算改进的马尔科夫模拟值
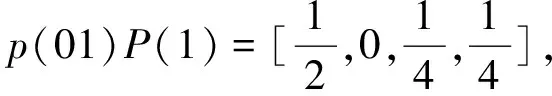
t2的数据处于E01状态,故设初始向p(02)=[1,0,0,0],则有:
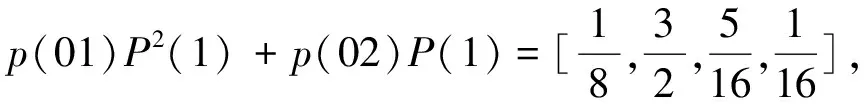
由表4可以看出,改进后模型的误差有了明显的降低,使用S型函数平滑处理原始数据的同时采用改进的计算公式计算模拟值能大大减小模型的误差。
3.3 利用模型预测
用灰色系统模型和灰色马尔科夫模型可以对未来的位移值进行预测。预测结果见表5。
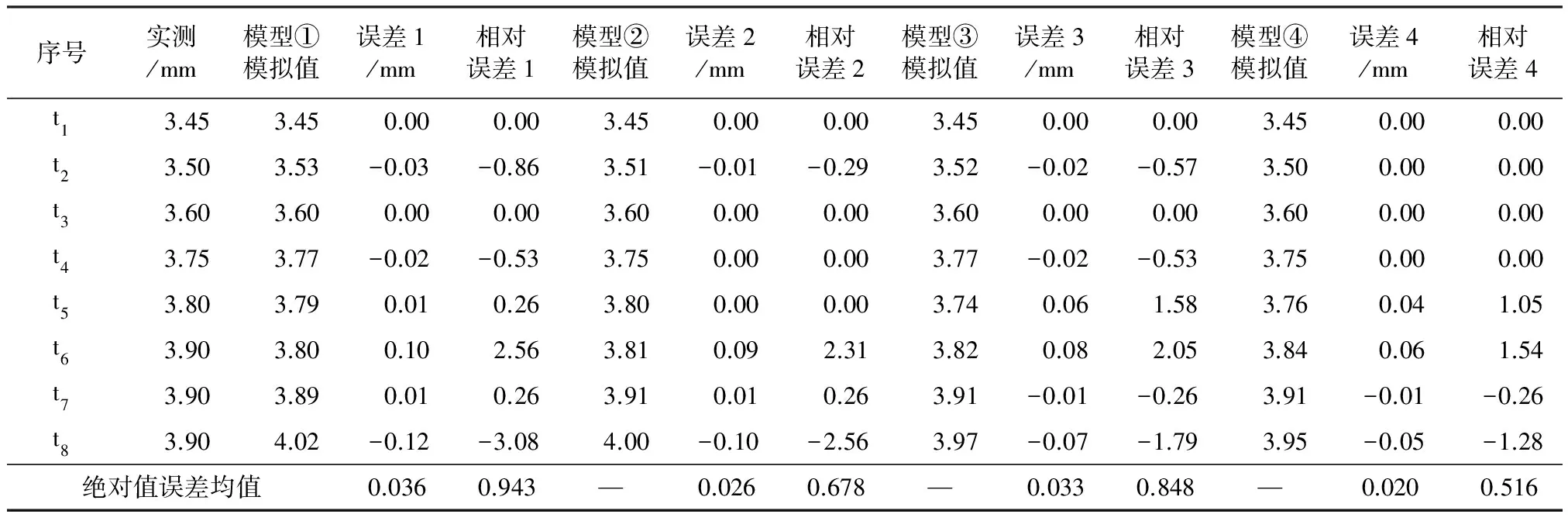
表4 改进马尔科夫模拟值与马尔科夫模拟值对比
4 结 论
本文针对传统的不等时距灰色马尔科夫预测模型的不足,用经过S型函数平滑后的数据建立不等时距GM(1,1)模型,改进不等时距马尔科夫GM(1,1)模型模拟值和预测值的计算方法,对路基边坡位移进行了模型检验和位移预测。初步得出以下结论:
(1) 模型③在模型①的基础上误差和相对误差分别减小了8.33%和10.07%,采用S型函数平滑处理数据,能使数据变得平滑,进而减小模型的误差。
(2) 模型②在模型①的基础上误差和相对误差分别减小了27.78%和28.10%,而模型④在模型①的基础上误差和相对误差分别减小了44.44%和45.28%,使用改进的公式计算不等时距马尔科夫模拟值能大大提高模型的预测精度。
(3) 随着时间延续,不等时距马尔科夫模型的模拟精度下降。
[1] 张 闯,彭振斌,彭环云.曲线回归分析模型在边坡位移预测中的应用研究[J].路基工程,2016(3):64-66.
[2] 王雪红,刘晓青,陶海龙,等.优化BP神经网络的位移预测模型[J].水利水运工程学报,2014(2):39-42.
[3] 蔡泽宏,简文彬,李宏达,等.基于滑坡监测数据的时间序列位移预测[J].水利与建筑工程学报,2016,14(1):237-242.
[4] Deng Julong. The unit of introduction representation in grey system theory[J]. The Journal of Grey System, 1991,3(2):87-106.
[5] 刘思峰.灰色系统理论及其应用[M].北京:科学出版社,2010.
[6] 赵晓艳,刘天娇,周 波,等.灰色模型GM(1,1)的平滑改进及其应用[J].东北电力大学学报,2006,26(4):64-66.
[7] 刘 戈,仝国柱.基于灰色BP神经网络组合模型的深基坑周围沉降预测研究[J].天津城建大学学报,2016,22(3):185-189.
[8] 时合生,樊爱宛,王 巍.用马尔科夫残差修正灰色理论的煤炭需求预测[J].计算机仿真,2011,28(10):187-190.
[9] 毛占利,朱 毅,杨伯忠,等.火灾事故的灰色-马尔科夫模型预测研究[J].中国工程科学,2010,12(1):98-101.
[11] 侯翔龙,阳 辉.基于滑动无偏灰色马尔科夫模型的水库降雨量预测[J].水土保持通报,2014,34(3):182-184.
[12] 刘淑官,黄声享,徐北海,等.基于无偏灰色马尔科夫链的基坑沉降预测研究[J],测绘地理信息,2015,40(4):11-13.
[13] 李明然,田林亚,洪 毅.改进的灰色马尔科夫模型在大坝变形中的应用[J].水利与建筑工程学报,2012,10(3):65-66.
[14] 卢 丹.改进的灰色_马尔科夫模型在地下水水质预测中的应用研究[J].水利规划与设计,2106(6):86-99.
[15] 陆兴华,姜 涛,秦斯成.改进的灰色马尔科夫模型在煤层沉降预测中的应用[J],煤炭技术,2015,24(2):188-192.
[16] 杨世安.优化的灰色马尔科夫模型在建筑物沉降预测中的应用[D].上海:华东理工大学,2014:21-39.
Application of Improved Unequal time Interval gray Markov Model in Roadbed Slope Displacement Prediction
HU Hua1,2,3, XIE Jinhua1,2
(1.CollegeofArchitectureandCivilEngineeringofXiamenUniversity,Xiamen,Fujian361005,China;2.XiamenUniversityTanKahKeeCollege,Zhangzhou,Fujian363105,China;3.ResearchInstituteofXiamenUniversityinShenzhen,Shenzhen,Guangdong518057,China)
Grey Markov model has been widely used in displacement prediction, but the accuracy of the predicting results obtained from the unequal time interval gray Markov model directly established by using the actual measurement data is low, and the error of using the traditional formula to calculate the unequal time interval gray Markov simulation value and the prediction value is large. In response to these deficiencies, this paper studies the application of an improved unequal time interval gray Markov model in slope displacement prediction. First, the actual measured data of a side slope in Xiamen are smoothed by using the S function, and then the unequal interval grey GM(1,1) model was established with the smoothed data, finally the improved formula was adopted to calculate the Markov simulation value and predictive value. Results show that the improved unequal interval grey Markov GM(1,1) model's fitting precision and prediction precision has been greatly improved, and it has some reference value to the slope stability prediction.
grey Markov Model; slope displacement prediction; sigmoid function
10.3969/j.issn.1672-1144.2016.06.001
2016-08-19
国家自然科学基金资助项目(51278437);广东省自然科学基金资助项目(2014A030313006);福建省自然科学基金资助项目(2015J01224)
胡 华(1968—),男,湖北孝感人,教授,主要从事岩土力学、岩土工程减灾等方面的研究工作。 E-mail:xmhuh@xmu.edu.cn
谢金华(1988—),男,湖北随州人,硕士研究生,研究方向为岩土工程数值模拟。 E-mail:1043129437@qq.com
U416.1+4
A
1672—1144(2016)06—0001—06
