基于统计分析的江苏省雾霾影响因素研究
2017-01-11顾静,李想,李娜,江畅
顾 静, 李 想, 李 娜, 江 畅
(南京邮电大学地理与生物信息学院,江苏南京 210023)
基于统计分析的江苏省雾霾影响因素研究
顾 静, 李 想, 李 娜, 江 畅*
(南京邮电大学地理与生物信息学院,江苏南京 210023)
为对江苏省雾霾的治理提出有针对性、科学有效的措施,综合运用多元统计分析、主成分分析和因子分析等方法,对江苏省各地级市的雾霾影响因素和空气质量指标(AQI)的关系进行了对比分析。结果表明:江苏省第二产业占比、面积和人均机动车拥有量与雾霾污染均呈负相关。最后提出江苏省第二产业占比小和占地面积小的城市应更加注重雾霾污染的防治,江苏省人均机动车拥有量小的城市应更加重视制定和执行限制机动车排放的相关规定,江苏省13个地级市应更加注重雾霾防治的经验交流,进行多城市联合治理雾霾。
雾霾影响因素;多元统计分析法;非参数检验;因子分析;主成分分析
雾霾不仅污染生态环境,还严重影响人类的身心健康。李金岚[1]研究认为,雾霾天气能见度较低,极易引发交通事故,危害人类生命财产安全。张军强[2]研究认为,雾霾中的颗粒污染物不仅会引发心肌梗塞,造成心肌缺血或者损伤,还易使人产生悲观情绪,甚至导致心理疾病。目前,各国学者对雾霾的研究主要集中于气候特征、影响因素、危害和治理措施,尤其是对雾霾影响因素的研究较多。学者多从气象和能源消费结构2个方面对雾霾的影响因素进行研究。由于气象存在许多不确定因素,因此笔者不予研究。在能源消费结构方面,李振宇等[3]研究认为,煤、石油、天然气等能源的消费是大气污染物的主要来源。关于雾霾的影响因素,学者通过理论分析和统计分析进行了研究。但是理论分析仅停留在口头,缺乏科学论证方法的支持,没有说服力。王珊等[4]对1960—2012年西安地区雾霾日数与气象因素变化规律进行了研究。徐相明等[5]对上海徐家汇和奉贤雾霾日数气候变化特征进行了分析。整体来看,学者运用统计分析方法对雾霾影响因素的研究多停留在气象学方面,对生产生活中污染源与雾霾的相关性研究较少。笔者通过选取2014年1月江苏省各地级市各种可能影响雾霾产生因素及雾霾的相关数据,分别运用多元统计分析法、主成分分析法和因子分析法对雾霾天气成因进行定量分析,并提出缓解江苏省雾霾现状的建议,旨在为江苏省雾霾防治提供科学依据与借鉴。
1 材料与方法
1.1 研究方法
1.1.1 Spearman相关系数检验。 利用非参数检验中的Spearman相关系数检验来判断雾霾的主要影响因素。有效弥补雾霾的测度变量——空气质量指标(Air Quality Index,AQI)及其影响因素的分布事先未知的缺陷。Spearman相关系数设置如下:
(1)
相关系数γs的概率分布为
(2)
其中,
(3)
1.1.2 Kendall-τ相关系数检验。Kendall-τ相关系数可以用来表示正负相关性。为了使结果更加精确,同时采用非参数检验中的Kendall-τ相关系数检验与Spearman相关系数检验,共同判断雾霾的主要影响因素。τ相关系数设置如下:
(4)
τ的概率分布为
(5)
其中,
(6)
1.1.3 多元线性回归分析。多元线性回归模型是指有多个解释变量的线性回归模型,用于解释被解释变量与多个解释变量之间的线性关系,多元线性回归的数学模型为
y=β0+β1x1+…+βpxp+ε0
(7)
式中,ε0为随机误差,满足
E(ε0)=0,var(ε0)=σ2
(8)
对式(7)求期望,则有
E(y)=β0+β1x1+…+βpxp
(9)

(10)
1.1.4 主成分分析。主成分分析是通过对原始变量相关矩阵或协方差矩阵内部结构关系的研究,利用原有变量的线性组合,将具有相关性的多个原始变量形成几个综合指标(主成分)。这些主成分既可以反映原来多个变量的大部分信息,又互不重叠。主成分分析的每个主成分都是各原始变量的线性组合,即
Fi=∑X,i=1,2,…,p
(11)
其中,Fi为主成分,X为原始变量,∑为协方差矩阵。
X=[X1X2…Xp]T
(12)
αi=[αi1αi2…αip]T
(13)
(14)
(15)
(16)
1.1.5 因子分析。 因子分析是将众多原始变量浓缩成少数几个公因子变量,使得公因子变量具有较强可解释性的一种多元统计分析方法。若干个原始变量被分解成公因子的线性组合,即
Xi=ai1F1+ai2F2+…+aipFp+ei,i=1,2,2…,q
(17)
其中,F为公因子,aij为因子载荷,ei为特殊因子。
1.2 城市的选取 笔者选取了江苏省南京、无锡、徐州、常州、苏州、南通、连云港、淮安、盐城、扬州、镇江、泰州、宿迁13个地级市进行研究。
1.3 指标的选取
1.3.1 空气质量指标。选取2014年1月13个地级市每日的AQI数据,并选择将1月的AQI相加取平均值来反映该月的空气质量水平。
1.3.2 衡量城市规模的指标。GDP、面积和人口数量均来源于《江苏省统计年鉴2014》。
1.3.3 衡量机动车排放污染的指标。机动车量、人均机动车保有量、单位面积机动车量。关于机动车辆,选取截至2013年12月的机动车保有量。由于江苏省13个地级市的规模不同,为了增加可比性,通过2个间接指标来表示城市的机动车量情况,分别为单位面积机动车量和人均机动车保有量。其中,单位面积机动车量是为了将机动车量与城市面积规模相结合,人均机动车保有量是为了将机动车量与城市人口规模相结合。
单位面积机动车量(万辆/ km2)=机动车量(万辆)/各地面积(km2)
人均机动车保有量(辆/人)=机动车量(万辆)/各地人口(万人)
1.3.4 衡量工业排放污染的指标。包括第二产业增加值、第二产业占比、工业主要污染物排放量。第二产业是指按“三次产业分类法”划分的国名经济中的一个产业部门。第二产业的企业大多是污染排放大户,其生产规模在一定程度上能代表工业排放污染水平。
第二产业占比=各地第二产业增加值(亿元)/各地GDP总值(亿元)
对于工业排放污染,由于各个城市所处地区及经济发展水平不同,直接的第二产业增加值可比性不足,因此,笔者选取2013年第二产业增加值占GDP的比值来表示各地的工业规模。工业主要污染物排放量是指工业二氧化硫和工业烟粉尘排放量。这些数据来源于国家数据网,笔者选取了2013年数据。
1.4 变量设置 根据“1.3”中的指标进行变量设置,如表1所示。
2 结果与分析
2.1 多元统计分析 绘制散点图,观察Xi(i=1~9)与Y(AQI)之间的关系(图1)。从城市规模来看,AQI与人口、面积GDP都没有明显的线性关系或非线性关系(图1a~c)。从机动车污染排放来看,机动车拥有量人均机动车拥有量与AQI没有明显的线性关系或非线性关系。但是AQI与人均机动车拥有量呈较明显的负相关趋势(图1d~f)。从工业污染排放来看,第二产业增加值和工业主要污染物排放量与AQI都没有明显的线性关系或非线性关系。但是AQI与第二产业占比呈明显的负相关趋势(图1g~i)。
2.2 统计检验 由于数据选取的是江苏省13个地级市的单月数据,难以完全根据散点图判断AQI与各影响因素的相关性。为了检验AQI和各潜在因素的相关性,采用非参数检验方法对各影响因素进行相关性检验。为了使结果更精准,采用Spearman相关系数和Kendall-τ 相关系数同时进行检验。相关性检验结果见表2。
由于Spearman 相关系数检验在第2类和第3类各有1个变量与Y显著相关,所以将选取Spearman 相关系数检验中的置信度(单侧)为0.01的结果并结合散点图进行分析。从城市规模来看,X1、X2、X3与Y没有相关性。由此可知,江苏省雾霾的影响因素与城市规模无关。
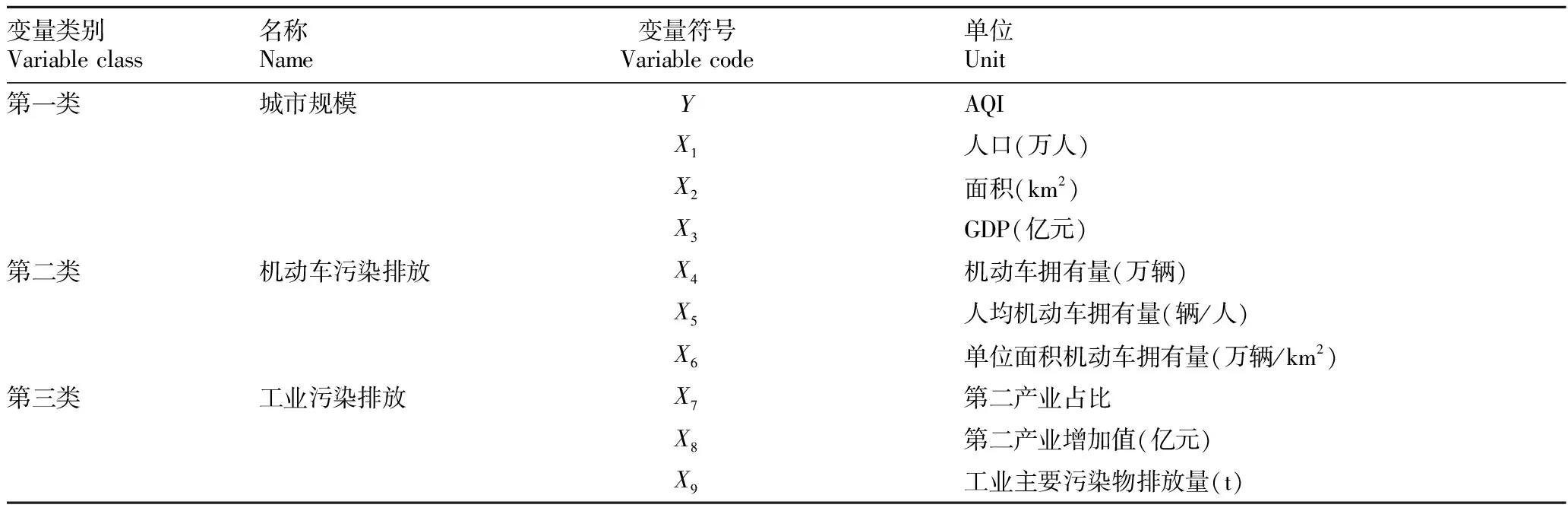
表1 变量设置

图1 各指标与AQI的关系Fig.1 Relationship between different indexes and AQI
从机动车污染排放来看,X4、X6与Y无显著相关性,但X5有明显的负相关趋势。机动车拥有量绝对值多的城市一般都对机动车排放标准有着严格的规定和管理,如苏州等城市。因此,机动车的绝对拥有量与AQI无显著相关性。污染较严重的城市(如徐州等),人口较多,但机动车拥有量相对较少,而污染程度较轻的城市(如苏州等),人口相对较少,但机动车拥有量相对较多,因此AQI与人均机动车拥有量呈负相关。

表2 显著的变量及其检验相关系数
注:**表示在置信度(单侧)0.01水平显著相关;*表示在置信度(单侧)0.05水平显著相关。
Note: * * indicated significant correlation at the 0.01 level of confidence (Unilateral); * indicated significant correlation at the 0.05 level of confidence (Unilateral).
从工业污染排放来看,AQI与X9和X8的绝对值均无关。但X7与AQI呈显著负相关。通过数据对比和查阅资料发现,江苏省整体经济水平相对较高,近年来,对工业污染物的排放等纷纷加强整治措施,而江苏省第二产业占比高的城市由于产值高,治理投资费用也相应较大,即X7与AQI呈显著负相关。对X5、X7和Y进行多元分析,回归模型为
Y=β0+β1X5+β2X7
(18)
式中,β0、β1、β2为待估参数。
由已知数据,利用SPSS进行回归分析,结果表明,R2为0.503,拟合优度较好,因此可接受该模型。由表3可知,该模型为
Y=161.804-21.368X5-18.852X7
(19)
表明人均机动车拥有量和第二产业占比越大的城市,雾霾治理效果越好,雾霾污染的可能性越小。
2.3 主成分分析和因子分析 以主成分分析法作为提取因子的方法,采用因子分析法进行分析,以X1~X9作为原始变量,结果见表4。由表4可知,X1、X2的特征值大于1.000,X3的特征值接近于1.000,且X1、X2、X3的累加贡献度为96.058%,能够解释原始变量的大多数信息。因此,提取的3个公因子(F1、F2、F3)较为合理,使用这3个公因子对江苏省13个地级市的雾霾影响因素进行分析。

表3 变量回归结果
由于部分变量初始载荷矩阵的大小差异不显著,因子的实际含义模糊不清,无法命名,因此使用方差最大正交旋转法进行因子旋转,使得变量在某个因子载荷趋于1.000,其他趋于0。旋转后的因子载荷矩阵如表5所示。由表5可知,公因子F1在X1、X3、X4、X5、X6、X8、X9的载荷较大,可以命名为除面积和第二产业占比外的其他公因子(简称为其他公因子);公因子F2在X2上的载荷较大,可以命名为面积因子;公因子F3在X7上的载荷较大,可以命名为第二产业占比因子。
由主成分分析法及表5可知,公因子F1、F2、F3的模型可分别用下式表示:
F1=0.890X12+0.981X3+0.984X4+0.829X5+0.842X6+0.950X8+0.915X9
(18)
F2=10.939X2
(19)
F3=0.915X7
(20)
表明F2与X1、X3、X4、X5、X6、X8、X9呈正相关,即人口、GDP、第二产业增加值、主要污染物排放量、机动车与其他因子呈正相关;F2与X2呈负相关,即面积因子与面积呈负相关;F3与X7呈正相关,即第二产业占比因子与第二产业呈正相关。

表4 因子分析结果

表5 旋转后的原始因子载荷矩阵
绘制提取的3个公因子与AQI的散点图,如图2所示。从图2可见,F1、F3与AQI呈负相关,F2与AQI呈正相关。由主成分分析和因子分析结果可知,X1、X3、X4、X5、X6、X8、X9与F7成正相关,由图2可知,F1与AQI呈负相关,因此X1、X3、X4、X5、X6、X8、X9与AQI呈负相关;F2与X2呈负相关,与AQI呈正相关,因此面积与AQI呈负相关;F3与X7成呈相关,与AQI呈负相关,因此X7与AQI呈负相关。综上可得,X1、X2、X3、X4、X5、X6、X7、X8、X9与AQI呈负相关。
3 结论与建议
笔者利用2014年1月江苏省的AQI数据,结合江苏省统计年鉴的相关数据,采用多元统计分析法和主成分分析、因子分析法相结合的2种方法,分别对江苏省的主要雾霾影响因素进行了分析。第1种方法以反映雾霾严重程度的AQI作为Y,以城市规模、机动车排放、工业污染排放等9个变量作为X,分别与Y绘制散点图,并进行非参数检验,分析它们之间的相关关系。然后对显著的变量进行多元线性回归分析,发现第二产业占比、人均机动车拥有量是显著影响因素,具体表现为:①第二产业占比与雾霾污染呈负相关,因为第二产业占比越大的城市对雾霾污染的治理越严格,措施越全面;②人均机动车拥有量与雾霾污染呈负相关,这是由于人均机动车拥有量多的城市对机动车排放的规定严格,执行力度更加彻底。

图2 AQI与公因子的散点Fig.2 Correspondence analysis between AQI and components
第2种方法以主成分分析为提取公因子的方法,对城市规模、机动车污染排放、工业污染排放等9个变量进行因子分析,提取公因子,进而对公因子与AQI进行散点图分析,最终得出城市规模、机动车排放、工业污染排放等9个变量与AQI呈负相关。
通过以上2种方法对江苏省13个地级市的AQI影响因素进行分析,均得出第二产业占比、面积、人均机动车拥有量与AQI呈负相关。该结论有悖于常理。这是由于工业污染重、人均机动车多、面积大的城市虽然很容易出现雾霾,但这些城市已经提前采取多项措施对雾霾进行防治,如南京在雾霾多发季,一些重污染企业常常停产。从该结论也可以看出,江苏省雾霾较严重的城市(如南京等)的治理措施有效,江苏省雾霾相对较轻的城市(如扬州、南通等)应采取更为有效的治理措施,更加重视雾霾的治理与防治。
通过对以上分析,笔者提出如下缓解雾霾污染的有效方法:①第二产业占比小和占地面积小的城市应更加注重雾霾污染的防治;②人均机动车拥有量小的城市应更加重视制定和执行限制机动车排放的相关规定;③江苏省13个地级市应更加注重雾霾防治的经验的交流,进行多城市联合治理雾霾。
[1] 李金岚.论雾霾天气的成因危害及防治措施[J].资源节约与环保,2013(10):146.
[2] 张军强.雾霾的现状及治理措施[J].河南农业,2014(21):33-34.
[3] 李振宇,黄格省,李项杰,等.从能源消费结构分析北京雾霾天气成因及防治措施[J].古代石油石化,2013(6):12-16.
[4] 王珊,修天阳,孙扬,等.1960-2012年西安地区雾霾日数与气象因素变化规律分析[J]. 环境科学学报, 2014,34(1): 19-26.
[5] 徐相明, 顾品强,李聪.上海徐家汇和奉贤雾、霾日数气候变化特征分析[J]. 大气科学研究与应用, 2014(2): 55-64.
[6] 薛薇,SPSS统计分析方法及应用[M].3版.北京:电子工业出版社,2013:186.
Research on the Influential Factors of Fog in Jiangsu Province Based on the Statistical Analysis
GU Jing, LI Xiang, LI Na, JIANG Chang*
(Nangjing University of Posts and Telecommunications, College of Geographic and Biologic Information, Nanjing, Jiangsu 210023)
In order to put forward targeted for fog haze of governance in Jiangsu Province, scientific and effective measures, multivariate statistical analysis method, principal component analysis, factor analysis and other methods are integrated to study relationship between AQI and haze influence factors of each city in Jiangsu Province. The result showed that the proportion of the second industry, area and per capita volume of motor vehicles of Jiangsu Province have a negative correlation with the fog and haze pollution . Finally, the second industry of Jiangsu Province area than small and should pay more attention to the city covers an area of prevention of haze pollution, vehicle ownership per capita in Jiangsu Province small city should pay more attention to the formulation and implementation of the relevant provisions of restrictions on vehicle emissions, 13 prefecture level cities in Jiangsu Province should pay more attention to the haze prevention of the exchange of experience, multi city joint governance haze.
Haze influencing factor; Multivariate statistical analysis; Non-parametric test; Factor analysis; Principal component analysis
顾静(1995- ),女,江苏连云港人,本科生,专业:测绘工程。*通讯作者,讲师,硕士,从事遥感信息的处理和应用。
2016-09-30
S 181.3
A
0517-6611(2016)34-0105-05
