T检验在公安决策中的应用

王二院， 李 侠

(中国人民公安大学公安管理学院， 北京 100038)

T检验在公安决策中的应用

王二院， 李 侠

(中国人民公安大学公安管理学院， 北京 100038)

随着大数据时代的到来，警务工作的数字化趋势进一步加强，应用统计技术完善传统的警务定性判断成为警务改革的重要环节。论述3种T检验技术在公安决策中的应用：(1)单样本T检验,比较单一样本均值与已知数值的差异性；(2)两个独立样本T检验，比较两个独立样本均值的差异性；(3)两个配对样本T检验，比较两个配对样本均值的差异性。

T检验； 单样本； 独立样本； 配对样本； 公安决策

0 引言

T检验是用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著。它与Z检验、卡方检验并列。T检验是戈斯特为了观测酿酒质量而发明的。戈斯特于1908年在《Biometrika》期刊上公布T检验，但因其老板认为其为商业机密而被迫使用笔名student。

2016年9月19日作者利用中国知网检索“T检验”篇名关键词，2013年以来的全部文献共有97篇。其中最近一篇论文为“应用t分布统计量和t检验统计量介绍假设检验原理”(秦国友； 赵耐青；中国卫生统计, Chinese Journal of Health Statistics, 2016年04期)。检索“公安T检验”篇名关键词，2013年以来的全部文献共有23篇，但缺乏T检验的内容。检索“警察T检验”篇名关键词，2013年以来的全部文献共有4篇，同样缺乏T检验的内容。

1 T检验技术理论

1.1 基本概念

T检验就是利用假设检验的思想，对平均数的差异进行检验。鉴于T检验技术的主要理论基础是T检验，本文认为公安T检验技术是T检验在公安实践中的具体应用。当然，方差已知时用Z检验法和多个总体T检验的F检验是T检验技术的另外两种情形。

T检验技术可以检验定性警务分析的结论，增强警务工作的可信度，指明警务工作的方向。本文研究的T检验技术包括3种：①单样本T检验；②两个独立样本T检验；③两个配对样本T检验。

T检验的一般步骤是：建立假设；计算统计量；查标准值；作出判断。

1.2T检验的软件操作过程

在“IBM SPSS Statistics 21”(后文简称为SPSS)环境下T检验的操作过程基本包括3个步骤。

(1)建立数据文件。

(2)打开对话框。选择菜单栏中的【Analyze(分析)】→【Compare Means(比较均值)】,打开“T检验”主对话框，如图1所示。

图1 “T检验”主对话框

根据实践需要分别选择以下4种模块实现T检验过程：(a)One-SampleTTest；(b)Independent-SampleTTest；(c)Paired-SampleTTest；(d)One-Way ANOVA。

(3)结果分析。统计软件会直接给出P值，其检验判断规则如下(双侧检验)：

如果概率P值小于或等于显著性水平α，则拒绝零假设H0；

如果概率P值大于显著性水平α，则接受零假设H0；

如果将以上理论应用于公安实践则可以将公安定性决策分析升华为公安定量决策分析。

2 应用单样本T检验比较公安民警工资与全国平均工资

2.1 问题描述

2016年5月13日国家统计局发布《2015年全国平均工资统计》，数据显示,2015年全国城镇非私营单位就业人员年平均工资62 029元；年平均工资最高行业是金融业114 777元；年平均工资最低行业是农林牧渔业31 947元。

某市公安局从全局民警中随机抽取了30人，核算其2015年工资，数据如表1。请问某市公安局民警的工资与全国金融业、农林牧渔业的年平均工资有无显著差异。

2.2 理论分析

单样本T检验是比较某一样本的平均数与某一确定总体均值是否有统计学意义上的差异。例如，前文“2.1”某市公安局30名民警平均工资与城镇非私营单位就业人员年平均工资是否有显著性差异？可以运用单样本T检验来解决这个问题。

2.3 软件操作

首先解决某市公安局民警的工资与全国的年平均工资有无显著差异的问题，后两个问题可类推。进行如下假设检验：H0:μ=62 029;H1:μ≠62 029。

(1)打开对话框。根据表1建立数据文件“1.sav”，选择菜单栏中的【Analyze】→【Compare Means】→【One-Sample T Test】命令，弹出【One-Sam-ple T Test】对话框。

表1 某市公安局30名民警2015年工资

(2)选择检验变量和样本检验值。

(3)设置显著性水平。

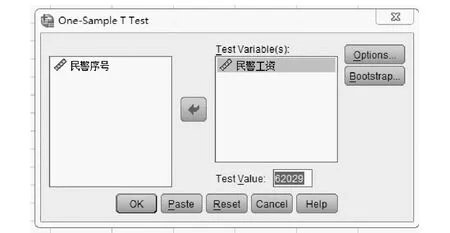
图2 “单样本T检验”主对话框

(4)结束操作。单击【OK】按钮，完成操作。此时，软件输出结果出现在结果浏览窗口中。

表2 One-Sample Statistics

表3 One-Sample Test

2.4 公安决策

(1)描述性统计量表

表2呈现了单个样本的描述性统计量的值，包括参与统计的单个样本的个案数(N)、均值、标准差和均值的标准误。

(2)单样本T检验结果报表

表3呈现了单样本T检验的结果，包括T值、自由度(df)、检验的概率(Sig.)、均值差值，以及差分的95%置信区间。如表3所示，本案例T检验的T值为-24.855，自由度df=29，双侧T检验的概率Sig.(双侧)=0.000。由于显著性水平为0.05，而0.000<0.05，因此拒绝零假设，即某市公安局民警的工资与全国的年平均工资相比有显著差异, 且显著偏低。

(3)某市公安局民警的工资与金融业、农林牧渔业的年平均工资有无显著差异。

(4)某市公安局民警的工资与金融业的年平均工资有无显著差异。

参照前述2.3步骤，结论如下：因为t=-144.100, Sig. (2-tailed)=0.000，所以某市公安局民警的工资与金融业的年平均工资有显著差异，且显著偏低。

(5)某市公安局民警的工资与农林牧渔业的年平均工资有无显著差异。

参照前述2.3步骤，结论如下：因为t=43.150, Sig. (2-tailed)=0.000，所以某市公安局民警的工资与农林牧渔业的年平均工资有显著差异，且显著偏高。

3 应用两独立样本检验技术比较两个交警的管理水平

3.1 问题描述

随机抽选30名行人对十字路口的交通管理水平进行评分，满分10分。甲组30人对交警张三负责的十字路口A进行评分；乙组30人对交警李四负责的十字路口B进行评分；两个小组评分结果如表4所示。请问十字路口A和十字路口B的管理水平有无显著差异。

3.2 理论分析

本例要检验两个样本的均值是否有显著性差异。两独立样本T检验就是用来检验两个独立样本的均值之间是否显著差异，即检验两样本所代表的总体的均值是否相同。两个样本平均数差异检验要考虑两个样本所代表的总体是否正态分布，总体方差是否已知，还要考虑两个总体的方差是否齐性，两个样本是独立样本还是相关样本，两个样本的容量是否相同等问题。根据具体的条件还可以运用如下检验：Cochran-Cox-test、非参数检验、Z′检验。

表4 十字路口A和十字路口B的管理水平评分

3.3 软件操作

在SPSS中进行两独立样本T检验的操作过程如下。

设十字路口A和十字路口B的管理水平评分均值分别为μ1,μ2建立如下假设检验：

H0:μ1=μ2H1:μ1≠μ2。

图3 独立样本T检验主对话框

(1)打开对话框。根据表4建立数据文件“4.sav”，选择菜单栏中的【Analyze】 →【Compare Means】→【Independent-Sample T Test】命令，弹出【Independent-Sample T Test】对话框。这里变量sco表示两个交警的得分；变量x是不同交警的标志变量，1表示交警张三，2表示交警李四。

(2)选择检验变量和分组变量。

(3)定义组别名称。(4)完成操作。单击【OK】按钮，完成操作。此时，软件输出结果出现在结果浏览窗口中。

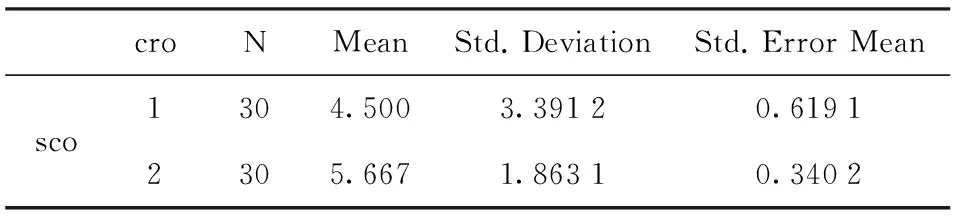
表5 Group Statistics

表6 Independent Samples Test

3.4 公安决策

(1)描述性统计量表

表5分别呈现了分组变量的简单描述性统计量，包括参与检验数据的个案数(N)、均值、标准差和均值的标准误。

(2)独立样本T检验结果报表

表6呈现的是对两独立样本进行T检验的结果，包括方差齐性检验的F值和概率，T检验的t值、自由度(df)和检验的概率，均值的差值，标准误差值和差分的95%置信区间。

表6中“Levene’s Test for Equality of Variances”下呈现的是检验方差齐性的F值(17.246)和显著性概率p(0.000)。因为P<0.05，拒绝F检验的零假设，即两总体的方差有显著性差异。所以以下皆参照“Equal variances not assumed”所对应的一行数据。

两独立样本T检验的值为t=-1.651，自由度df=45.045，双侧检验显著性概率P=0.106>0.05，因此接受两独立样本T检验的零假设，即两个样本所代表的总体的平均数相同，十字路口A和十字路口B的管理水平没有显著性差异。

4 应用两配对样本检验比较多个派出所常住人口和流动人口数

4.1 问题描述

为加强人口管理，某市公安分局对下辖的20个派出所分别进行调研，收集了相应的常住人口和流动人口数据(单位:人)，

如表7所示。试检验派出所常住人口和流动人口数是否存在显著差异。

表7 派出所常住人口和流动人口数据

4.2 理论分析

两配对样本T检验的目的是利用来自两个总体的配对样本，推断两个总体的均值是否存在显著差异。进行配对样本检验要满足3个要求：(1)两组样本的样本容量要相同；(2)两组样本的观察值一一对应；(3)总体服从正态分布。对两配对样本进行平均数差异检验，需要考虑数据的各种条件，从而选择合适的检验方法。

4.3 软件操作

数据类型属于配对样本的类型，故利用配对样本T检验来分析。

图4 配对样本T检验主对话框

(1)打开对话框。根据表7建立数据文件

“7.sav”，选择【Analyze】 →【Compare Means】→【Paired-Sample T Test】命令，弹出【Paired-Sample T Test】对话框。

(2)选择配对变量。

(3)完成操作。单击【OK】按钮，完成操作。此时，软件输出结果出现在结果浏览窗口中。

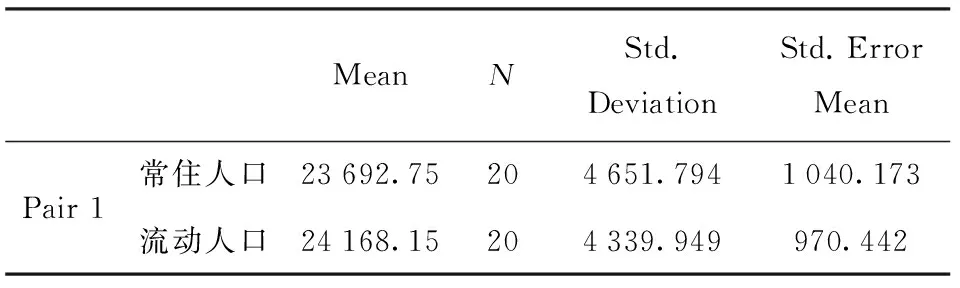
表8 Paired Samples Statistics

表9 Paired Samples Correlations

表10 Paired Samples Test

4.4 公安决策

(1)描述性统计量表

表8呈现了两配对样本的相关描述性统计量，包括：均值、样本容量(N)、标准差和均值的标准误。

(2)相关性检验结果报表

表9显示相关系数为0.804，显著性概率p<0.05，因此在95%的置信水平上差异显著，即常住人口和 流动人口人数显著相关，符合用配对样本T检验的前提条件。

(3) 配对样本T检验结果报表

表10呈现的是配对样本T检验的结果，包括两配对样本差分的均值、标准差、均值的标准95%的置信区间，还有T检验的t值、自由度(df)和显著性概率(Sig.)。配对样本T检验的t值为-0.752，自由度(df)为19，显著性概率p=0.461>0.05，因此在95%的置信水平上差异不显著，即各派出所常住人口和流动人口人数无显著差异。

5 应用T检验技术的注意事项

在公安实践中应用T检验技术时应注意以下5点：

(1)注意适用条件

可以通过观察数据的分布或进行正态性检验估计数据的正态假设。方差齐性的假设可进行F检验，或进行更有效的Levene检验。由于公安实际数据很难获得，本文所有公安数据仅有参考价值，请读者关注数据处理方法即可。

(2)选取检验区间

单侧检验的界值小于双侧检验的界值，因此更容易拒绝，犯第Ⅰ错误的可能性大。T检验中的P值是接受两均值存在差异这个假设可能犯错的概率。

(3)区分判别规则

当一个统计量的值落在临界域内，这个统计量是统计上显著的，拒绝零假设。反之是统计上不显著的，不拒绝零假设。

(4)结合公安实际

P越小，不是说明实际差别越大，而是说越有理由拒绝零假设，越有理由说明两者有差异；然而差别有无统计学意义和有无公安实践上的实际意义并不完全相同。

(5)慎用方差分析

进行两组以上T检验，需要用方差分析进行比较，方差分析被认为是T检验的推广，但原始数据必须满足复杂的条件。

[1] CLEVELAND M，FAVO C M，FRECKA T J，et al. Trends in the International Fight Against Bribery and Corruption[J]. Journal of Business Ethics，2009：199-244.

[2] WOO H，WON S，CHANG K Y，et al. Comparison of muscle activity between two adult groups according to the number of Shaker exercise[J]. Journal of Oral Rehabilitation，2014，41(6)：409-415.

[3] 梁铁成.警察心理健康状况之调查[J].中国健康心理学杂志，2007(11).

[4] 王飞，邹舒.刑警与监管民警的个性心理特质比较研究[J].四川警官高等专科学校学报，2007(4).

[5] 王璐，王沁，等.SPSS统计分析基础、应用与实战精粹[M].北京：化学工业出版社，2012:74-99.

[6] 贾俊平.统计学[M].北京：清华大学出版社，2006:264-297.

[7] 张文彤,钟云飞.IBM SPSS数据分析与挖掘实战案例精粹[M]. 北京：清华大学出版社, 2013:102-116.

[8] 佚名. 去年各行业年平均工资出炉. http:∥edu.gmw.cn/newspaper/2016-05/15/content_112453410.htm.

(责任编辑 陈小明)

王二院(1972—)，男，安徽宿州人，副教授，硕士研究生导师。研究方向为公安管理学。

D035.39