一种多子阵合成孔径声纳成像算法研究*
2017-01-11陈晓辉
殷 钊 彭 成 陈晓辉 杨 博
(1.92677部队 大连 116000)(2.水声对抗技术重点实验室 湛江 524022)
一种多子阵合成孔径声纳成像算法研究*
殷 钊1彭 成2陈晓辉2杨 博2
(1.92677部队 大连 116000)(2.水声对抗技术重点实验室 湛江 524022)
论文基于二阶泰勒展开公式和双根号方程的等价变换,对多子阵合成孔径声纳的双根号斜距历程进行级数近似,在此基础上推导了快速成像算法所必须的二维频域系统函数,并提出了一种多子阵合成孔径声纳距离-多普勒成像算法,计算机仿真实验验证了论文方法的正确性。
合成孔径声纳; 多子阵; 级数近似; 距离-多普勒算法
(1. No. 92677 Troops of PLA, Dalian 116000)
(2. China Science and Technology on Underwater Acoustic Antagonizing Laboratory, Zhanjiang 524022)
Class Number TP391
1 引言
多子阵技术[1~3]通过方位向多个接收阵元组成的接收阵列,成功地解决了距离向测距和方位向高分辨之间的矛盾,使得合成孔径技术在水声领域开始走向工程实用的道路。然而这种构型增加了成像算法的复杂性,必须对传统基于收发合置SAS的成像算法加以改进。
相位中心近似方法(Phase Centre Approximation,PCA)[4~5]将一对收发分置的阵元等效为其中间一个虚拟的收发合置阵元,然而内在的二维空变转换误差会导致近距离的目标散焦。将传统方位维拆分成阵元维(同一个脉冲内不同阵元接收的信号)和脉冲维(不同脉冲内同一个阵元接收的信号),就可以把多子阵SAS成像转化为多个双基SAS成像问题[6~10],基于此思想,文献[9]和文献[10]分别基于二阶泰勒近似和数值分析方法提出了一种该模型下的R-D成像算法,但前者“停-走-停”假设会产生较大的相位误差;而后者驻相点求解过程中数值分析方法的采用降低了算法实用性,文献[11]提出了一种基于Loffeld双站公式(Loffeld’s Bistatic Formula,LBF)方法[12]的线频调变标(Chirp Scaling,CS)成像算法,然而LBF内在的近似使得其不能用于近距离和宽波束情况。
本文利用根式的等价变换[7]和级数近似方法将每个双基SAS的双程斜距历程转化成类似于传统收发合置SAS的斜距历程,然后利用R-D成像算法对每个双基SAS进行成像处理,便可以得到多幅粗分辨图像,在此基础上将多幅粗分辨图像进行相干叠加便得到最终的高分辨SAS图像,仿真实验验证了本文方法的可行性和有效性。
2 多子阵SAS成像几何
多子阵SAS二维成像几何如图1所示,距离向为r轴,平台的运动方向为方位维,即x轴,平台在运动的过程中,以固定的脉冲重复频率向正侧视方向发射线性调频信号p(τ)。
(1)
其中rect(τ)为门函数,宽度为脉冲宽度Tp;γ为调频率,τ为距离向快时间。
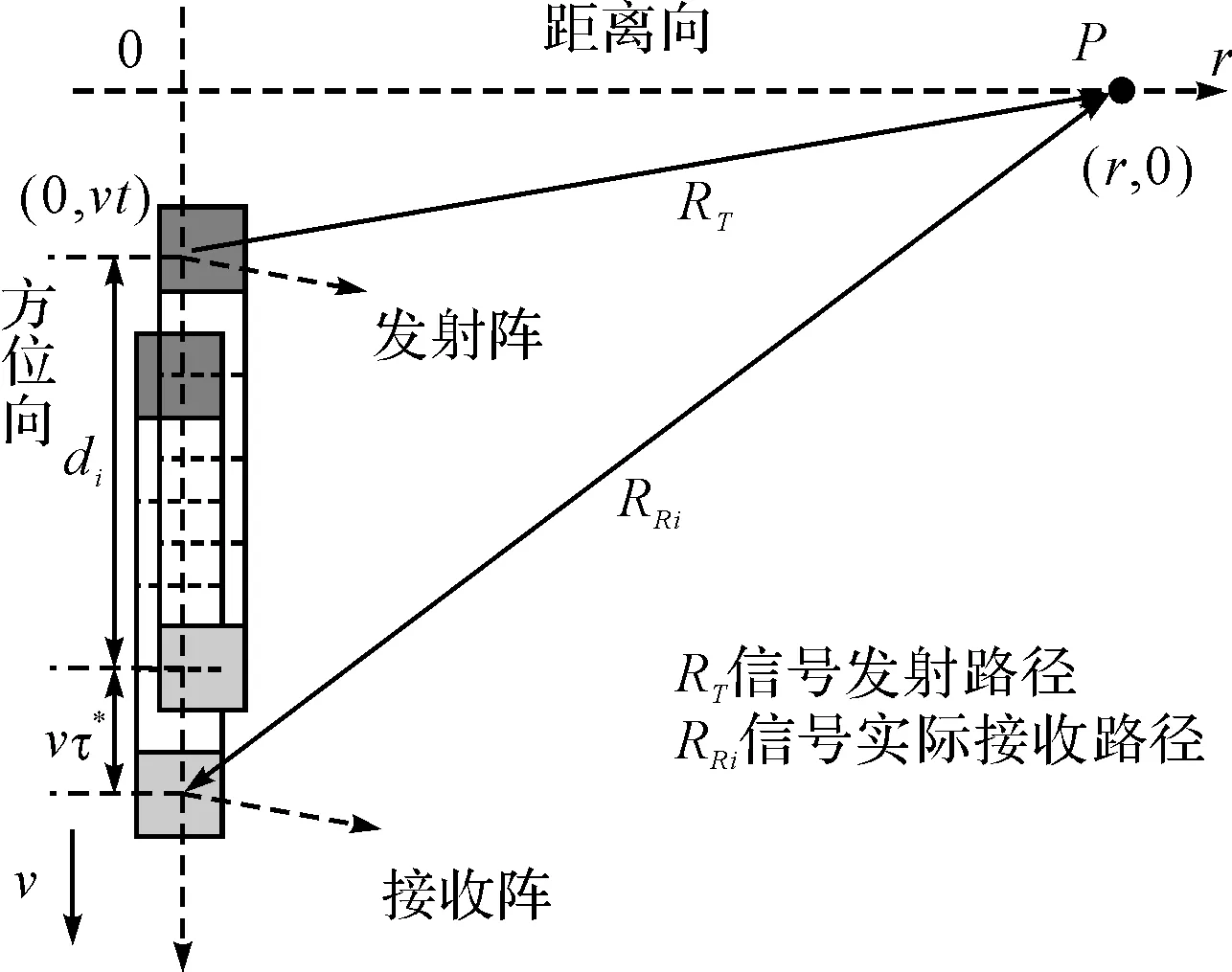
图1 多子阵SAS成像几何
假设二维空间中存在一个理想点目标,其二维坐标为(r,0),那么当平台运动到v·t位置时,第i个接收阵元与发射阵元所组成子系统的双程斜距历程为
Ri(t;r) =RT(t;r)+RRi(t;r)
(2)
其中tRi≈2r/c+di/v,其物理意义在于相对于发射阵元信号发射时刻,接收阵元接收到信号时的时延量。
于是,第i个接收阵元收到的回波信号复包络可以表示为
(3)
其中c为水声声速;λ为对应于中心频率fc的波长;wa(t)为方位向窗函数,与滤波加权和收发阵元的波束形状有关。
3 多子阵SAS系统成像处理
3.1 二维频域系统函数
基于根式的等价变换,第i个接收阵元与发射阵元所组成子系统的双程斜距历程,即式(2)可以表示为
(4)

于是,式(4)可以表示为
(5)
观察式(5)可以发现,利用根式的等价变换和简单的代数运算后,子系统复杂的双根号斜距历程就可以用一个类似收发合置SAS的斜距历程来近似。
基于式(5),对点目标的回波信号完成距离向频域变换后,进行方位向傅里叶变换,即:
(6)
其中fτ为距离向瞬时频率,ft为方位向瞬时频率,相位项φi表达式为
(7)
基于相位驻留原理,可以得到相位驻留点,将此相位驻留点代入式(7)便可得到二维频域系统函数,即:
(8)

式(8)类似于传统收发合置SAS的二维频域系统函数的相位,于是多个双基SAS成像问题便转化为传统收发合置SAS成像问题。
3.2 R-D成像算法

(9)
基于式(9),针对第i个接收阵元和发射阵元所构成子系统的回波数据,所提出的R-D成像算法步骤如下。
步骤一:首先将回波数据变换到二维频域;
步骤二:对回波数据进行收发分置相位项的补偿,相位补偿函数为
(10)
步骤三:在二维频域对数据进行距离向脉冲压缩,其相位补偿函数为
(11)
步骤四:数据进行距离向傅里叶变换,将数据变换到距离-多普勒域进行距离徙动校正,其相位补偿函数为
(12)
步骤五:在距离-多普勒域进行方位向脉冲压缩,相位补偿函数为
(13)
步骤六:对数据进行方位向逆傅里叶变换。
对所有子系统数据安装上述步骤处理后便可得到多副粗分辨图像,对所有多副粗分辨图像进行相干叠加便得到最终的高分辨图像。
4 仿真实验
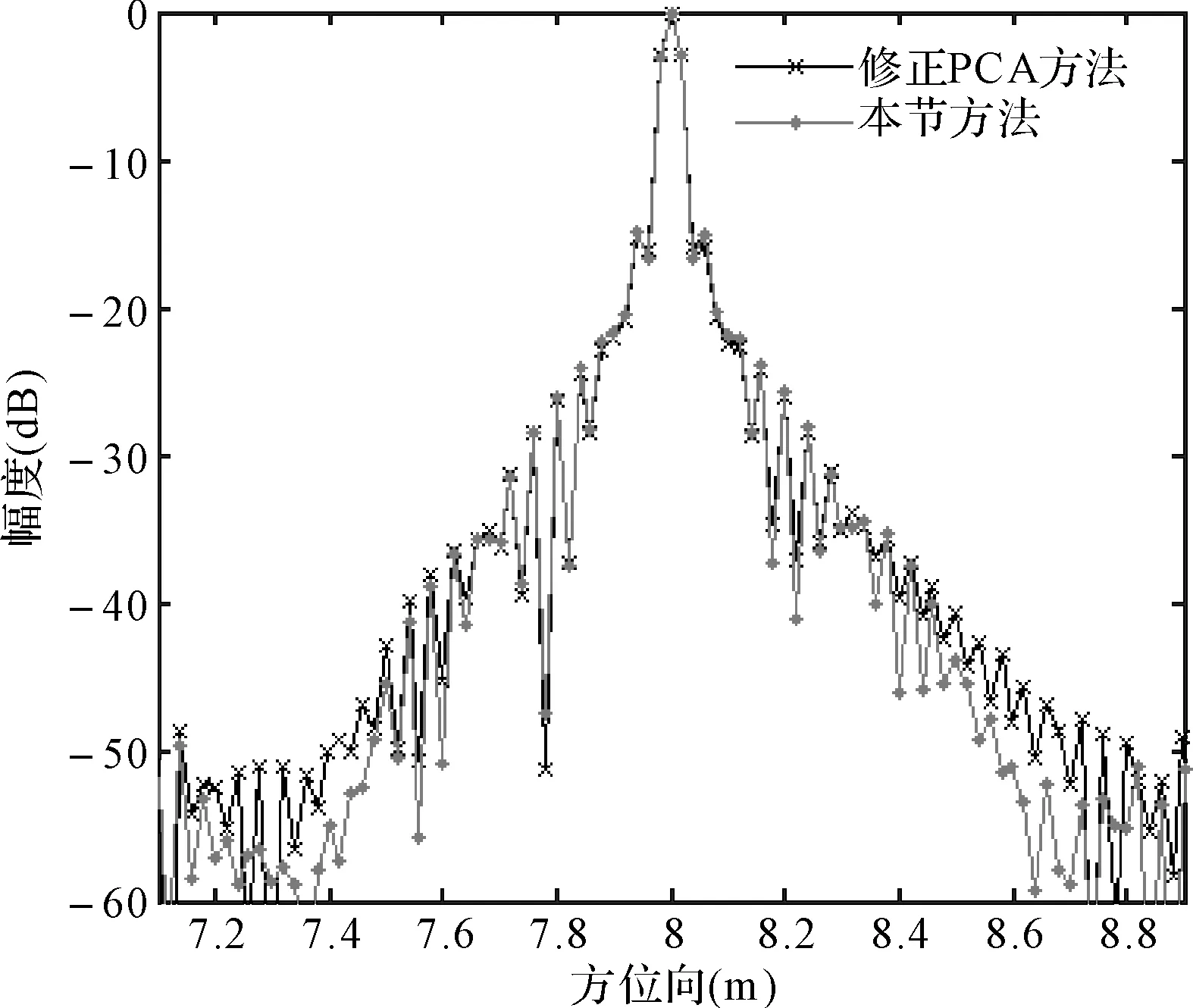
图2 理想点目标方位向剖面
为了验证本文提出的成像算法的有效性,本节设计了仿真实验。系统仿真参数为:信号中心频率为150kHz,信号带宽为20kHz,脉冲宽度为0.08s,脉冲重复周期为0.2s,发射阵方位向实孔径为0.08m,接收阵元方位向实孔径为0.04m,平台运动速度为2.5m/s。设置一个理想点目标,距离为110m,方位向坐标为8m,采用修正PCA方法[13]和本文方法成像后的结果如图2所示。
从对比中可以看出所提出的方法可以取得与修正PCA方法一致的成像结果,并且在局部细节上甚至还要优于修正PCA方法。在二维成像场景中设置五个点目标,如图3所示。

图3 仿真点目标场景图
点目标成像处理结果如图4所示,其中图4(a)为修正PCA方法[13]成像处理结果,图4(b)为本文方法成像处理结果。
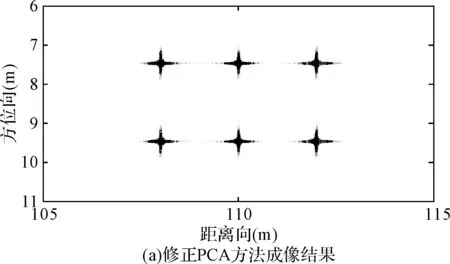

图4 点目标成像处理结果
从图4中可以看出本文方法能够取得与修正PCA方法一致的成像结果。因此本文方法是有效的。
5 结语
本文根据双根号的等价变换和级数近似方法,提出了一种新的距离-多普勒成像算法,相对于传统基于相位中心近似的方法而言,可以避免繁琐的空变二维相位误差的补偿,能够较好地补偿近距离和高阶相位误差,仿真实验验证了本文方法的正确性。
[1] M. P. Hayes, P. T. Gough. Synthetic aperture sonar: a review of current status[J]. IEEE Journal of Oceanic Engineering,2009,34(3):207-224.
[2] Douglas B L, Lee H. Synthetic-aperture sonar imaging with a multiple-element receiver array[J]. IEEE International Conference on Acoustics, Speech, and Signal Processing,1993,5:445-448.
[3] 张学波,唐劲松,钟何平.合成孔径声纳多接收阵数据融合CS成像算法[J].哈尔滨工程大学学报,2013,34(2):240-244.
[4] P. T. Gough, M. P. Hayes, D. R. Wilkinson. An efficient image reconstruction algorithm for multiple hydrophone array synthetic aperture sonar[C]//Proceedings of the Fifth European Conference on Underwater Acoustics(ECUA 2000), Lyon, France,2000:413-418.
[5] 张学波,唐劲松,钟何平,等.适用于宽波束的多子阵SAS波数域成像算法[J].哈尔滨工程大学学报,2014,35(1):93-101.
[6] H. J. Callow, M. P. Hayes, P. T. Gough. Wavenumber domain reconstruction of SAR/SAS imagery using single transmitter and multiple-receiver geometry[J]. Electronics Letters,2002,38(7):36-338.
[7] 张学波,唐劲松,张森.基于双基模型的多子阵合成孔径声纳CS成像算法[J].高技术通讯,2013,23(9):927-932.
[8] 张学波,唐劲松,张森,等.四阶模型的多子阵SAS距离-多普勒成像算法[J].电子与信息学报,2014,36(7):1592-1598.
[9] X. Jiang, C. Sun, J. Feng. A novel image reconstruction for synthetic aperture sonar with single transmitter and multiple-receiver configuration[C]//Proceedings of the IEEEOCEAN2004 Conference Proceedings, Kobe, Japan,2004:1940-1944.
[10] H. Yang, J. Tang, Q. Li, et al. A robust multiple-receiver Range-Doppler algorithm for synthetic aperture sonar imagery[C]//Proceedings of the IEEE OCEAN 2007 Conference Proceedings, Aberdeen, UK,2007:1-5.
[11] 张学波,唐劲松,张森,等.多接收阵合成孔径声纳线频调变标成像算法[J].系统工程与电子技术,2013,35(7):1415-1420.
[12] Loffeld O, Nies H, Peters V, et al. Models and useful relations for bistatic SAR processing[J]. IEEE Trans. Geosc. and Remote Sens.,2004,42(10):2031-2038.
[13] 杨海亮,张森,唐劲松.宽测绘带多子阵合成孔径声纳成像处理方法[J].系统仿真学报,2011,23(7):1424-1428.
An Imaging Algorithm for Multi-receiver Synthetic Aperture Sonar
YIN Zhao1PENG Cheng2CHEN Xiaohui2YANG Bo2
This paper uses two-order taylor expansion formula and the equivalent transformations of the radical function to approximate two double square rooted slant range history of multi-receiver synthetic aperture sonar (SAS). Based on that, 2-D frequency domain system transfer function, which is important for fast imaging algorithms is derived. Then, the paper presents range-Doppler (R-D) algorithm for multi-receiver SAS based on phase centre approximation (PCA) method. Lastly, simulated data is used to validate the presented processing method.
synthetic aperture sonar, multi-receiver, series approximation, range-Doppler algorithm
2016年6月7日,
2016年7月25日
国家自然科学基金(编号:61601473);装备预研基金(编号:9140C290401150C29132)资助。
殷钊,男,助理工程师,研究方向:信息与信号处理。彭成,男,硕士,助理工程师,研究方向:水声信号处理。陈晓辉,男,硕士,助理工程师,研究方向:水声信号处理。杨博,男,博士,工程师,研究方向:水声物理。
TP391
10.3969/j.issn.1672-9730.2016.12.035
