基于小波神经网络的波浪参数预报*
2017-01-11王红萍余义德
王红萍 余义德 张 丹
(91550部队 大连 116023)
基于小波神经网络的波浪参数预报*
王红萍 余义德 张 丹
(91550部队 大连 116023)
预报未来时刻水下航行体的出水姿态,关键在于海浪信息的预报。在获得实测海浪谱之后,还需对其进行预报,才能得到未来某时刻的海浪谱信息。使用Matlab软件完成小波神经网络的实际构建,利用测波雷达实测得到的海浪谱数据完成频谱预报,预报目标为6~8小时后的海浪频谱数据。最后经过仿真计算,小波神经网络方法可以对海浪谱进行较为精确的预报,海浪谱预报的有效时长可达6小时。
小波神经网络;波浪参数;预报
(No. 91550 Troops of PLA, Dalian 116023)
Class Number TB566
1 引言
研究证明,海浪具有非平稳非线性特征,为提高预报可信度需采用非线性方法。但目前对海浪机理的研究又不够深入,无法给出合适的非线性映射环节,几种基于数理统计的方法在应用上也比较困难。小波神经网络是人工神经网络与小波分析相结合而构造的一种新的神经网络模型[5~7]。将小波分析和神经网络模型相结合,结合了小波分析的时频局域化性质和神经网络的自学习能力,具有良好的非线性逼近能力[8~10]。综合上面因素,最终选择基于小波分析的神经网络法为本文的预报方法,即将小波分析作为神经网络中的一个环节,以小波函数作为神经网络中神经元的激励函数。实测海浪谱又可以分为海浪频谱和方向谱,下面分别就海浪频谱和方向谱的预报进行研究。
2 海浪谱预报方法
2.1 海浪频谱预报方法
时间序列,是指将研究对象的数量指标按时间次序排列起来的一系列数据,每一个时刻的数量指标能够一定在程度上代表研究对象在对应时刻所处的状态信息。时间序列可以被看作是由三个部分叠加而成,即趋势项、周期项和噪声项[1~3]。因此,时间序列包含了研究对象的状态随时间变化的规律信息,通过分析时间序列,可以完成得到研究对象的动态机制、预测研究对象的未来发展情况等目标,是一种十分有效的数据分析方法。
本文预报与常见预报有一点不同,即预报目标为谱,而通常预报目标为单个参数。基于此,采用分解子波—时间序列预报—合成频谱的模式,方法如下:
1) 编程实现小波神经网络模型的建立,并用随机数完成权值的初始化。
2) 对已采集的频谱时间序列,取每帧频谱中64个不同频率谱密度值,可得64组子波谱密度函数的时间序列。
3) 分别从各组时间训练数据中,以既定的规则抽取训练样本,作为神经网络的输入和输出,用上文所述过程对神经网络进行训练。
4) 利用完成训练过程的神经网络系统作为预报器,使用最新历史数据作为网络输入数据,所得网络输出数据作为所得的预报结果。并将各子波所得预报结果组合,形成所需要的频谱预报结果。
5) 在试验过程中,可选择有历史实测数据的部分作为预报目标时刻点,最后比较实测数据与预报结果,从而评估预报效果的好坏。
2.2 海浪方向谱预报方法
实测得到的海浪方向谱形式复杂,为便于计算和处理,采用ITTC(国际船模试验水池会议)假设,即假设方向谱在各个不同方向上的谱形是相同的,仅能量大小不同,海浪方向谱可看成海浪频谱与海浪方向函数的乘积[4~5]。此时海浪方向谱表达式变为
S(ω,θ)=S(ω)G(θ)
(1)
其中G(θ)被称为方向分布函数,代表海浪能量在不同方向上的分布。这种处理可使方向谱处理大大简化,且多数情况下与实际方向谱较为吻合。在这种假设下,通过对海浪频谱与方向分布函数分别预报进而得到海浪方向谱。其中频谱预报过程与上文相同,下面简要叙述对于方向分布函数的预报。
首先由海浪谱数据中提取出方向分布函数信息,方向分布函数公式为
(2)
其中,Sij(ω,θ)为各频率、方向子波谱密度,i取1~64,分别代表64个子频率;j取1~90,分别代表90个不同方向;mj0为每一方向频谱能量;G(θ)j代表第j个方向的方向分布函数值;m0为总能量,其值可由测波系统给出的三一波高数据求得:
(3)
式中Hs为海浪三一波高。
求出各方向谱数据方向分布函数并组成时间序列,再次利用小波神经网络系统,完成对方向分布函数的预报,再同频谱的预报结果组合,利用式(1),就可得到需要的方向谱预报结果。
但是需要指出的是,相较于海浪频谱,方向谱的预报时限相对较短,经过大量仿真计算得出,方向谱预报在3~5小时内能够取得较高的精度。
2.3 海浪谱评估方法
为评估海浪谱预报的精度,需要合适的评估方法。传统的评估方法多关注于几个主要的海浪参数,如有义波高、谱峰频谱、谱峰值、平均周期、谱尖度等,以其误差大小作为评价指标。该方法能够直接得到使用者最关心的结果,但所得结果为多个指标,且海浪参数对谱整体形状及内部精细结构的刻画不足。
海浪谱能够刻画海浪的能量分布,因此两不同海浪谱其谱形上重叠部分的多少能够反映两海浪谱的相似程度,这与直观经验是吻合的。对于频谱来讲,能量分布重叠率具体表现为两频谱重叠部分面积与两频谱所占总面积的比值。若将频谱所包围部分看作一个集合,则重叠部分定义为两频谱集合面积交集,总面积定义为两频谱集合的并集,能量分布重叠率即交集面积与并集面积的比值,如下式所示。
(4)
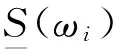
图1中频谱分别为不同时刻的海上实测谱和待评估频谱,阴影区域表示重叠部分。其中,图1(a)计算得出的EP值为0.807,图1(b)计算得出的EP值为0.917。该方法计算简单,能够较综合地反映两频谱的相似程度,具有简易、直观的特点,可用于一般评估,如要求更高的精度,可采用基于一阶矩的修正方法。
在实际评估应用中遇到如下情况:当EP值较高时,可以确定两被评估频谱相似度很高;而当EP值较低时,说明两频谱相似度较低,但无法确定两频谱不相似是由于能量大小的不同还是谱形的不同。

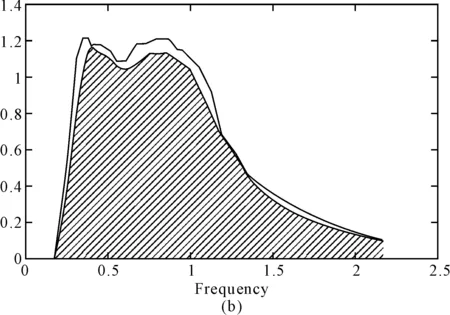
图1 能量分布重叠率评估方法效果图
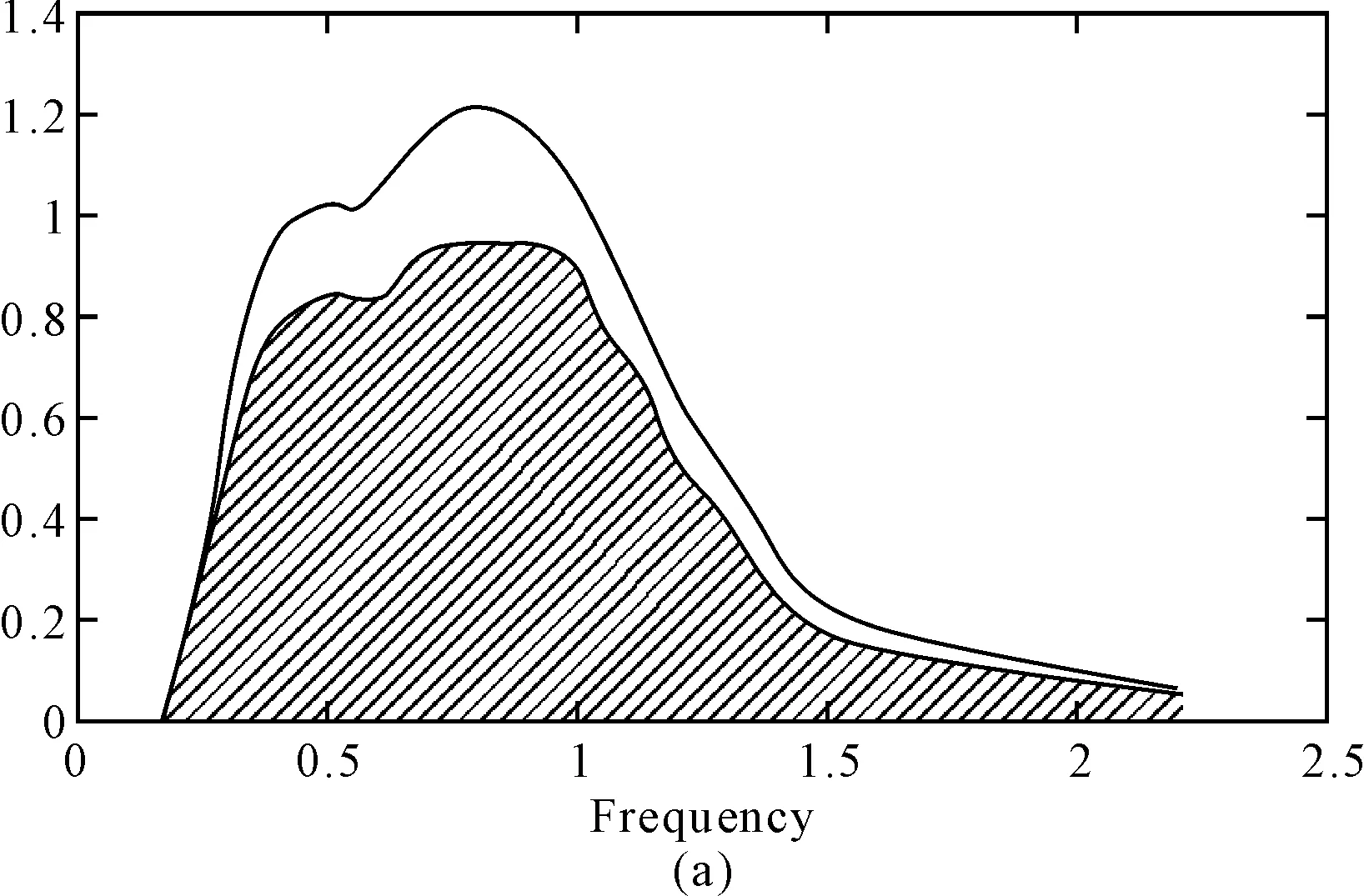

图2 一阶矩能量评估方法效果图
由于频谱的谱形代表能量分布,必须改善谱形对评估精度的影响。如图2所示,其中图2(a)EP值为0.8075,图2(b)EP值为0.8076。两组频谱EP值基本相同,但从评估的角度,认为图2(a)两频谱相似度更高。为此,提出了基于一阶矩的修正方法(前一种方法中面积可视为零阶矩),具体方法如下:
1) 首先确定重叠部分的型心位置,计算ωm使得:
(5)
2) 计算基于一阶矩的能量分布重叠率:
(6)
其中一阶矩取绝对值,是为了避免正负值抵消。
使用该方法后,图2(a)FEP=0.8084,图2(b)FEP=0.7104。从结果看,达到了区分谱形因素和能量因素比重的目的。
3 海浪谱预报
对海浪谱进行预报之后,即可得到数小时后精确的海浪信息。为验证该方法的可行性,选择多组实测海浪谱,进行导弹出水姿态的预报,仿真计算条件及结果分析如下。
经大量仿真计算研究表明,若要保证较高的预报精度,海浪频谱的预报时效约为6~8小时,海浪方向谱的预报时效约为3~5小时,具体时间因海浪谱而异。因此,为保证预报精度,选取有代表性的3组海浪谱(2组海浪频谱和1组海浪方向谱),采用前文所述方法,对海浪频谱分别进行1小时、2小时、3小时及6小时预报,对海浪方向谱分别进行1小时、2小时及3小时预报。在此基础上,采用CFD方法模拟海浪环境,并对导弹出水过程进行数值仿真,对不同海浪环境中导弹出水时的俯仰角速度及角位移进行计算,以预报导弹的出水姿态。
图3、图4为两组海浪频谱第1、2、3、6小时后的预报谱与实测海浪谱的对比图,其中WNN曲线代表经小波神经网络预报得到的预报谱,Target曲线代表实测谱。图中纵坐标为谱密度值,横坐标为频率值。
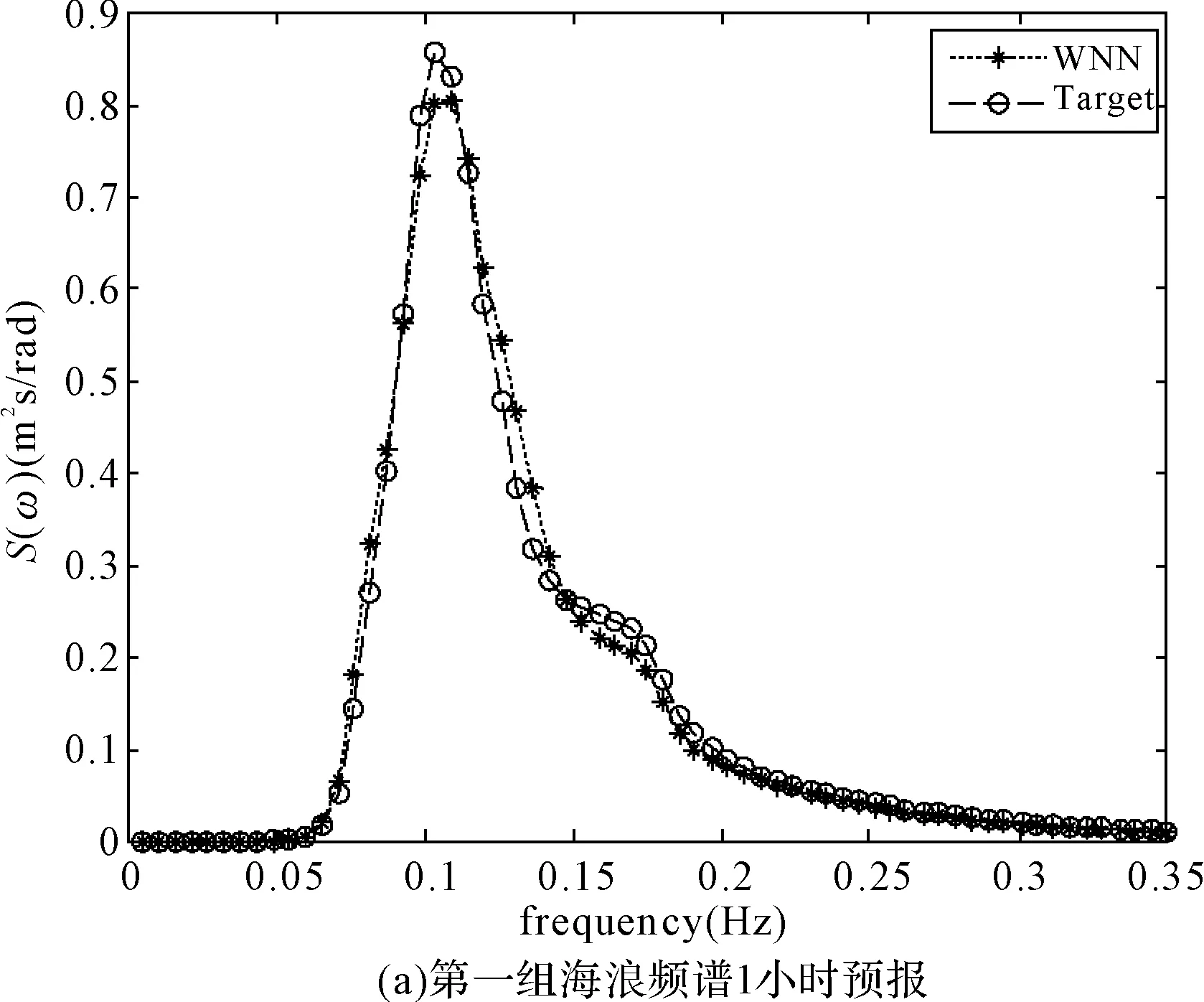
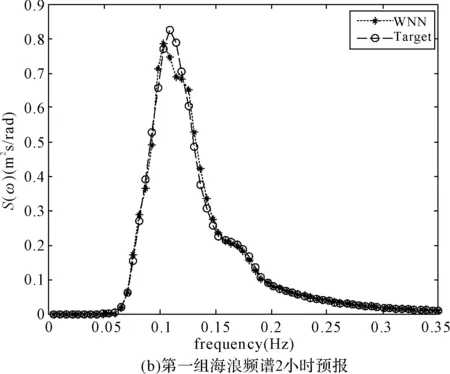
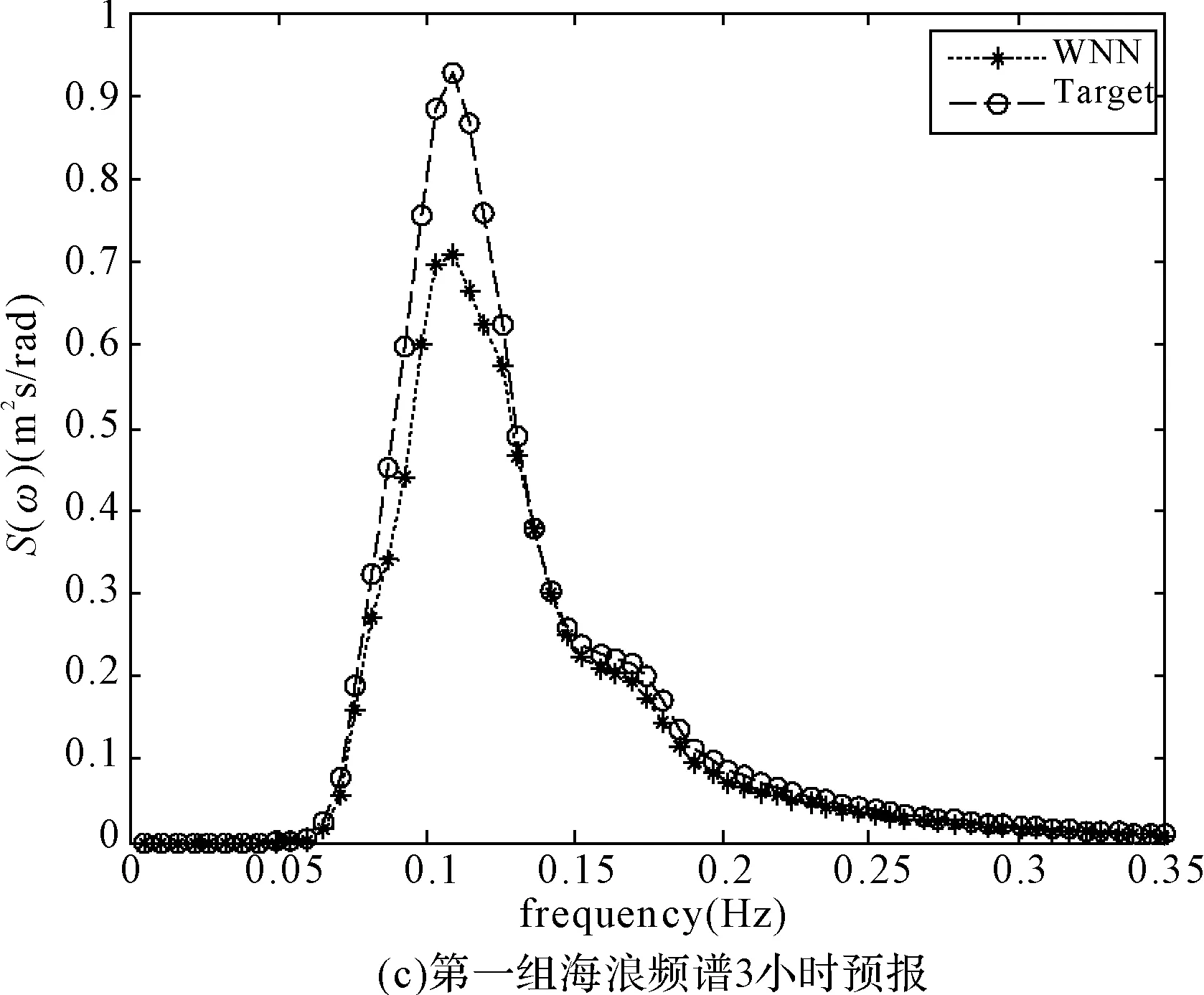

图3 海浪频谱预报结果
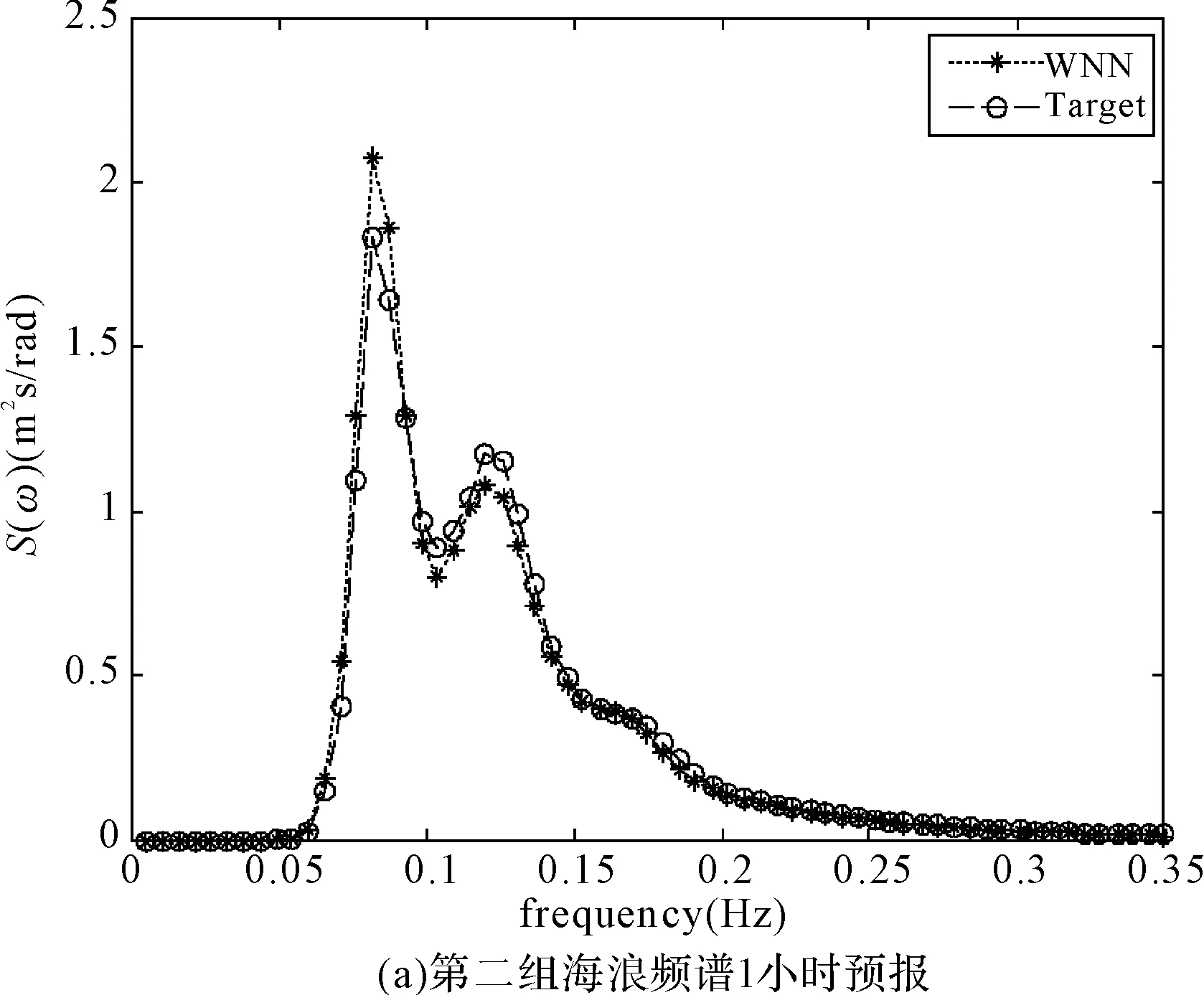

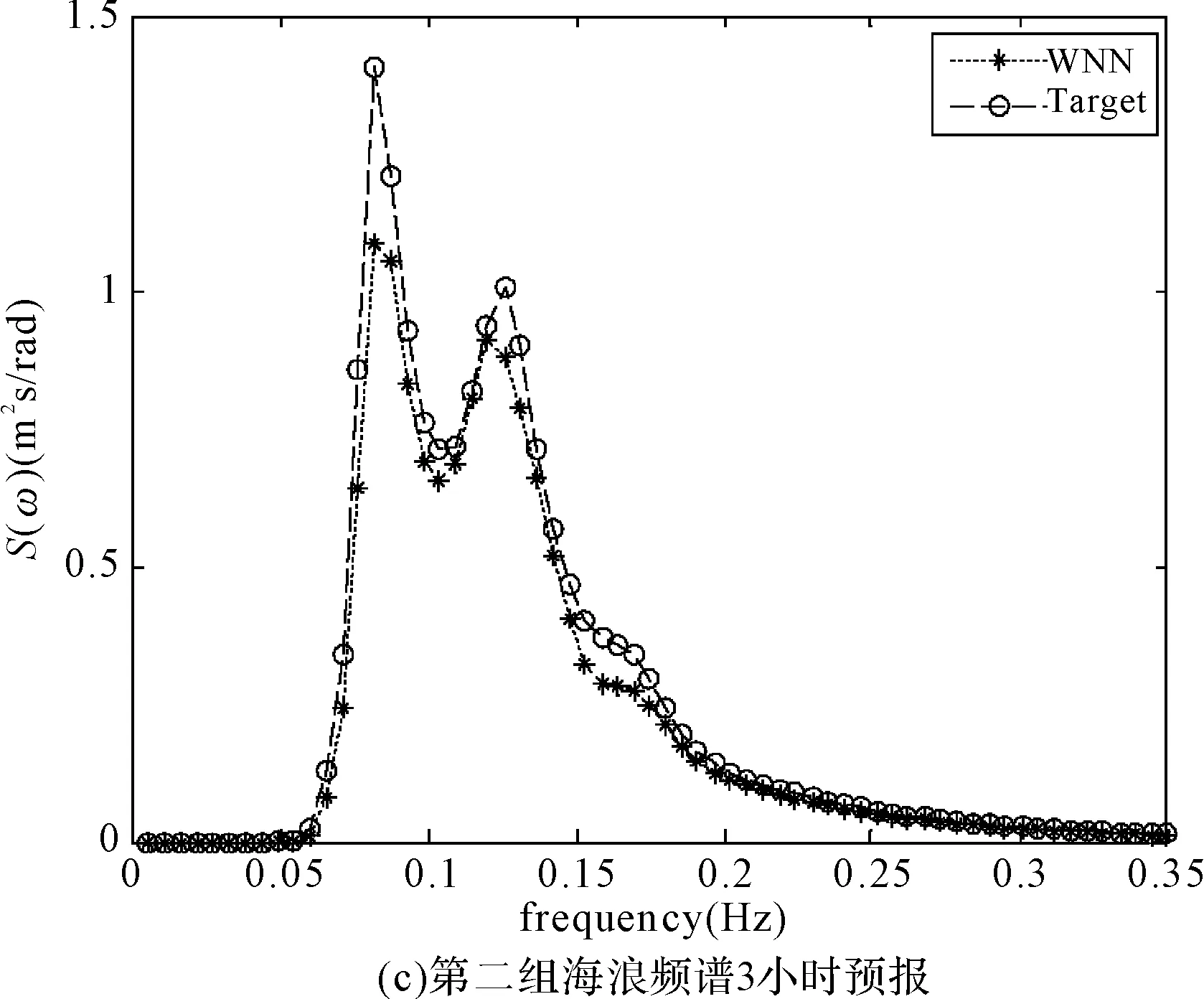

图4 海浪频谱预报结果
从图中可以看出:
1) 第一组海浪频谱为单峰谱,第二组为双峰谱,双峰谱呈现出较强的非线性特征。
2) 对于一组海浪频谱来讲,不同时长的预报结果谱型基本相同,说明在预报时长内,海浪谱基本保持连续性,海况基本平稳。
采用海浪谱评估方法对上述预报海浪谱进行评估,结果如表1所示。
图5为海浪方向谱方向分布函数第1、2、3小时的预报结果,WNN曲线代表小波神经网络预报结果,Target曲线代表实际值。

表1 海浪频谱评价结果

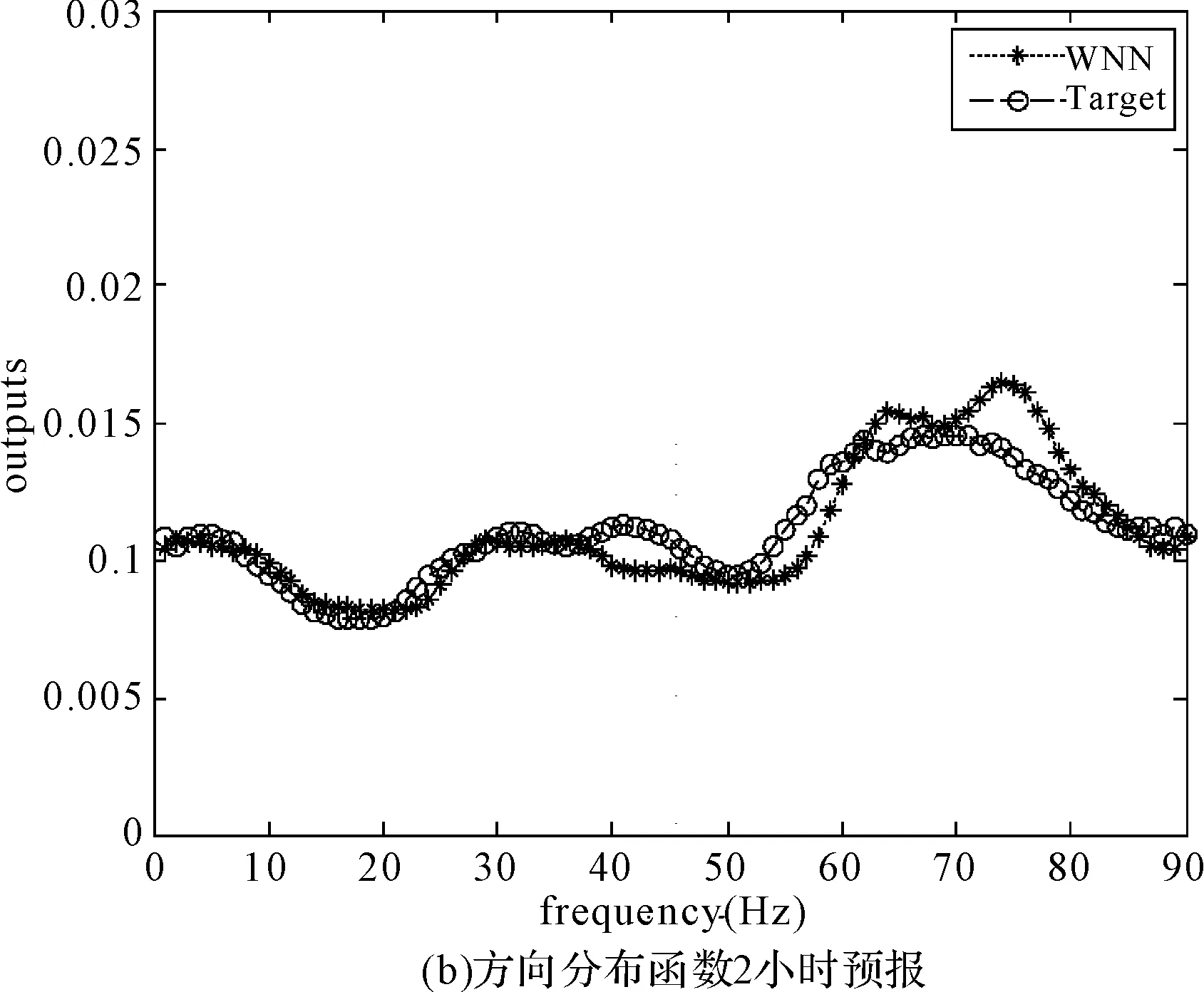
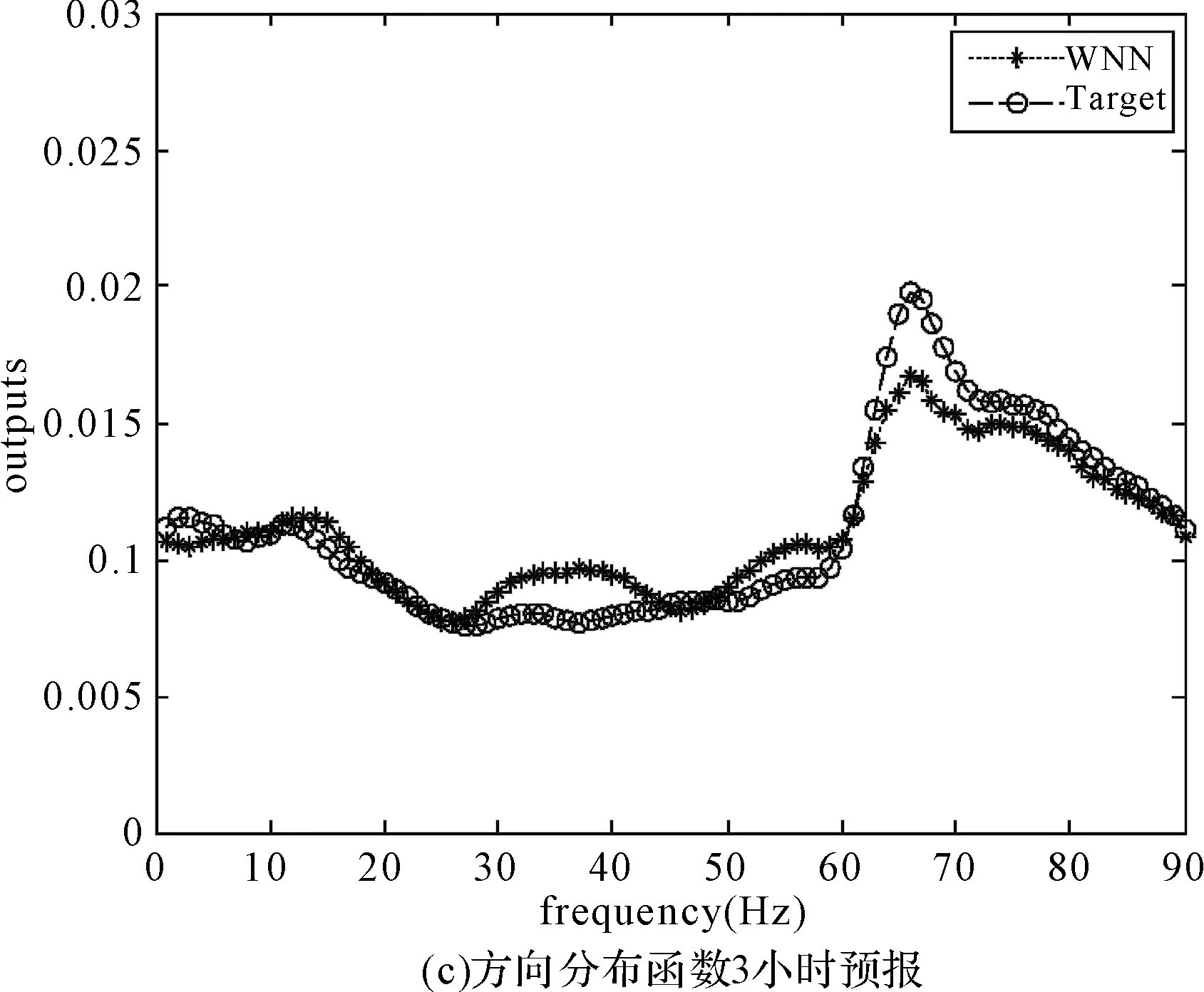
图5 海浪方向谱方向分布函数预报结果
从图中可以看出:
1) 方向谱预报结果与实测结果较为接近,尤其是对于方向谱的多峰性质均能体现。
2) 相对于海浪频谱,预报时长内方向谱方向函数的变化更为明显,但基本形状仍然相似,同样说明预报时长内海况基本保持平稳,变化平缓。
采用海浪谱评估方法对上述方向分布函数进行评估,结果如下表所示。从表2中可以看出,相对于海浪频谱,方向谱的预报精度稍差,但也可以基本满足工程需要。

表2 海浪方向谱方向分布函数评价结果
4 结语
采用海浪谱评估方法对海浪谱进行评估,所采取的WNN方法可以较好的对上述两种海浪谱进行预报,谱形及能量大小对比良好。经大量仿真计算研究表明,若要保证较高的预报精度,海浪频谱的预报时效约为6~8小时,海浪方向谱的预报时效约为3~5小时,具体时间因海浪谱而异。相对于海浪频谱,方向谱的预报精度稍差。
[1] 谷良贤,李军政.海浪对运载器姿态的影响研究[J]. 西北工业大学学报,1997,15(4):1-5.
[2] 鲁传敬.轴对称细长体垂直出入水[J].水动力学研究与进展,1990,12(4):35-40.
[3] 谢建辉,张宇文.海浪对鱼雷初弹道的影响分析与仿真[J].舰船设备科学与技术,1993,3(2):26-31.
[4] 刘曜.波浪对运载器出水姿态角的影响[J].舰船科学技术,2005,27(3):1-3.
[5] 刘家海,杨永全,张洪雨,等.二维数值水槽波浪生成过程及波浪形态分析[J].四川大学学报,2004,36(6):28-31.
[6] 李宏伟.数值水池造波方法研究[D].哈尔滨:哈尔滨工程大学,2009:5-41.
[7] 张勤,蒋廷臣,王秀萍.小波变换在变形监测分析中的应用研究[J].测绘工程,2005(1):8-10.
[8] Von Karman, T. & Wattendorf, F. L. The Impact on Seaplane Floats during landing NACA[R]. Technical Report Archive & Image Library.1929.
[9] Qi Peng. Hou Yijun. Numerical Wave Flume Study on Wave Motion Around Submerged Plates[J]. China Ocean Engineering,2003,17(3):397-406.
[10] LI. Benxia, Yu. Xiping. A 2-D Numerical Irregular Wave Tank and Its Verification[J]. Journal of Hydrodynamics,2005,17(2):222-227.
Wave Parameter Prediction Based on Wavelet Neural Network
WANG Hongping YU Yide ZHANG Dan
The key to predict wave lies to predict future exceeding water gesture of an underwater vehicle. On the basis of the measured spectrum, the information of wave spectrum is gained in the future.In this paper, firstly theory and method are studied to construct wavelet neural network by using Matlab. Secondly future spectrum after 6~8 hours can be forecast by analysis of data of wave observation radar .The simulation shows that this method is a high precision method to predict wave spectrum, thus possibly available for 6 hours.
wavelet neural network, wave parameter, prediction
2016年6月17日,
2016年7月20日
王红萍,女,硕士研究生,高级工程师,研究方向:水下测量。余义德,男,高级工程师,研究方向:水下测量。张丹,女,硕士研究生,助理工程师,研究方向:水下测量。
TB566
10.3969/j.issn.1672-9730.2016.12.019
