舰船运动对时间同步精度的影响*
2017-01-11付永杰
付永杰 于 蒙 李 迪
(92493部队89分队 葫芦岛 125000)
舰船运动对时间同步精度的影响*
付永杰 于 蒙 李 迪
(92493部队89分队 葫芦岛 125000)
论文针对海面运动舰艇需要高精密时间同步的问题,选择微波双向时间传递作为海面运动舰艇的时间同步方法。介绍了微波双向时间传递的基本原理,并通过对时间信号传输链路分析,得出了影响时间同步精度的误差来源。详细分析了信号在传播过程中由于舰船运动引起的时延误差,建立了由于舰船运动引起的时延误差数学模型,利用二阶泰勒展开式,推导出由两舰运动速度、加速度引起的时延误差。经计算,由于舰船运动引起的时延误差在0.05ns之内。该理论分析、计算可以为今后建立海面运动舰艇之间的时间同步系统提供理论依据。
时间同步;时延;舰船运动;泰勒公式
(Unit 89, No. 92493 Troops of PLA, Huludao 125000)
Class Number TB939
1 引言
精密的时间同步对于航空航天、时统通信、武器试验等具有重要的意义。当时间同步精度为100ns时,定位误差为30m,当时间同步精度为1ns时,定位误差为0.3m[1]。高精度的时间同步是通过高精度的时间传递手段来实现的。根据不同的时间同步精度需求,可以选择不同的时间传递方法。目前的精度较高的时间传递方法有卫星时间传递和双向时间传递[2]。双向时间传递又分为卫星双向时间传递[3]、光纤双向时间传递和微波双向时间传递[4]。其中微波双向时间传递是利用微波视距链路进行时间信号的传递。该方法时间同步精度高,传输稳定性好,系统建立和使用投入费用比卫星双向时间传递和光纤双向时间传递要低,但因其传输距离较短,只适用于视距距离内(300km以下),极大地限制了它的使用范围[5]。但是,利用微波进行双向时间传递的两个站点位置可以不固定,不需铺设光缆,它可用于视距距离内两个运动平台之间的时间同步,是适合海面运动节点时间同步的最佳方法[6]。
2 微波双向时间传递原理
微波双向时间传递基本原理是,两个观测站点在各自时钟的同一时刻在视距内发射时间同步信号,然后接收对方的时间同步信号,根据各自时钟的发送时刻和接收时刻信号的时刻来计算两站之间的时延,进而计算出两站之间的时钟钟差。通过校准后,实现两站之间的时间同步。图1为两运动节点时间信号传输示意图。A节点使用调制解调器将本地原子钟的时间信号经伪随机码调制,通过微波收/发信机将本地的时间信号发送给B节点,B节点接收由A节点发送过来的时间信号,解调信号后并与B节点的原子钟信号比较,从而测量A节点传到B节点的时间信号传递时延。在A节点发射信号的同时,B节点以同样方式发射信号被A节点接收。通过两节点数据交换,获得两节点原子钟之间的高精度钟差,进而校准之,最终实现两节点的时间同步。在微波双向时间传递过程中,由于传播信号路径的近似对称性,信号传输的时延原则上大部分被抵消。但在A、B两节点微波双向法时间传递过程中,由于设备时延、空间大气折射、节点船运动等因素的影响,时间间隔计数器的测量值并非两节点时间基准的真正差值,其中包含了诸多时延[7]。

图1 微波双向时间传递原理图
其中,TTA、TTB为A节点和B节点发射1PPS信号的时间;TRA、TRB为A节点和B节点接收到1PPS信号的时间;t0为标准的发射时间;TXA、TXB为A节点和B节点仪器发射时延,包括调制解调器发射时延;RXA、RXB为A节点和B节点仪器接收时延,包括调制解调器接收时延;TSA、TSB为A节点和B节点发射链路空气传输时延;RSA、RSB为A节点和B节点接收链路空气传输时延;TMA、TMB为A节点和B节点发射链路中由于节点船运动产生的时延;RMA、RMB为A节点和B节点接收链路中由于节点船运动产生的时延。
由图1得到,在微波双向时间传递中A节点的计数器读数TIA为
TIA=TTA-TTB+TXB+TSB
+TMB+RMA+RSA+RXA
(1)
B节点的计数器读数TIB为
TIB=TTB-TTA+TXA+TSA+TMA
+RMB+RSB+RXB
(2)
式(1)~式(2)并整理得两节点间钟差,即为两节点双向时间传递的时延:
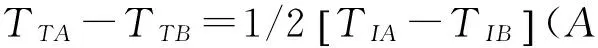

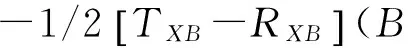



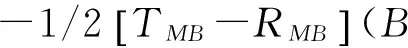
(3)
在微波双向时间传递中,虽然由于信号的传播路径近似对称,使路径的影响原则上大部分被抵消,但是仍然有一部分非对称性的因素影响了微波双向时间比对的精度。这些因素主要有: 1) 时间间隔测量引入的误差,约150 ps; 2) 设备的系统误差,约200ps~500ps[8]; 3) 信号空间传播路径上的误差,主要是空间大气折射率引起的时延,约几皮秒[9]; 4) 信号在传播过程中舰船的运动引起的时延误差,目前还未有文献介绍,是本文重点研究内容。
3 舰船运动引起的时延误差分析
同一舰艇编队的舰船在海面航行时,是处于实时运动状态。理想状态下,舰船匀速运行,两船之间相对速度为零,加速度为零,相对距离无变化,但在实际航行中,舰船处于实时运动状态,发射和接收时刻,两船之间的相对距离有变化,所以传输时延不为零。通过以下推算可以对由于舰船运动引起的时延误差进行估算。图2是A、B两船运动情况示意图。在t0时刻A船和B船同时通过本船上的天线向对方船发射时间信号,B船在tB时刻,A船在tA时刻,分别接收到对方发来的时间信号。此时,B船运动到了B′点,A船运动到了A′点。
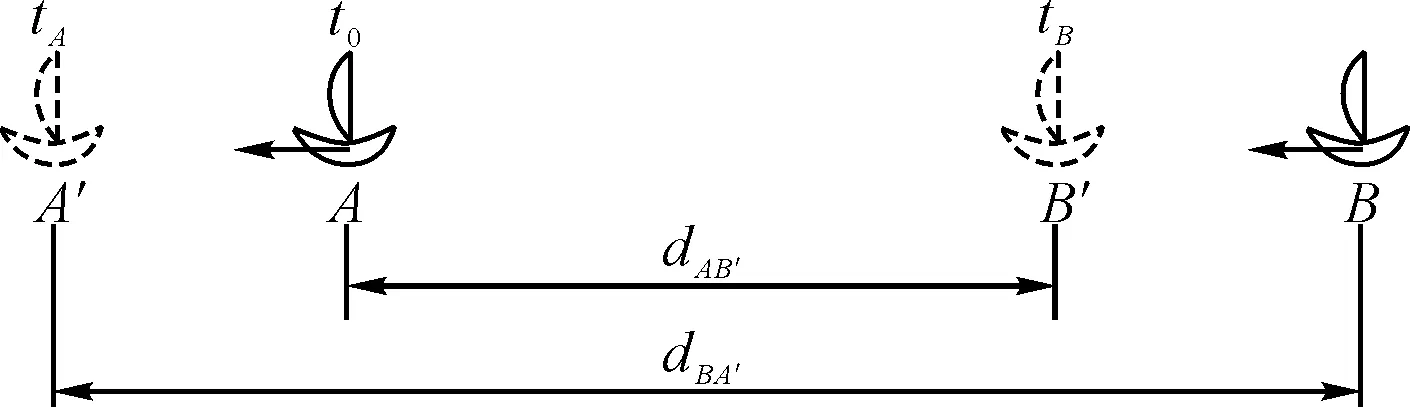
图2 A、B两船运动情况示意图
如果选取A船信号到达其发射天线相位中心时所对应的坐标时间t0作为归算时间,令XA(t0),XB(t0),XA′(t0),XA″(t0),XB′(t0),XB″(t0)分别表示A船与B船在归算时间t0的位置、速度和加速度,则几何距离时延tAB’可表示为
(4)
其中,dAB’为信号在t0时刻从A船发射天线中心出发,tB时刻被B船天线中心接收,这段时间内信号所经历的几何距离;XA(t0)为t0时刻A船的位置;XB’(tB)为tB时刻B船的位置;dAB为A船发射天线中心到B船接收天线中心的几何距离;ΔdAB为A船发射天线中心到B船接收天线中心的几何距离改正;c为光速,真空中的光速是299792458m/s,约等于3×108m/s。
dAB=XB(t0)-XA(t0)
(5)
对dAB’按泰勒公式在t0处展开到二阶,即加速度的一次幂有
(6)
则
(7)
则由几何距离改正引起的时延ΔτAB为
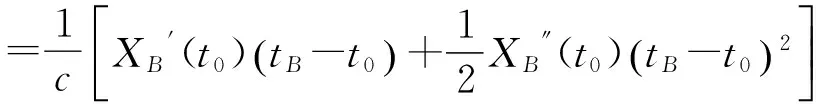
(8)
同理,信号在t0时刻从B船发射天线中心出发,tA时刻被A船天线中心接收,则几何距离时延tBA’可表示为
(9)
其中,dBA’为信号在t0时刻从B船发射天线中心出发,tA时刻被A船天线中心接收,这段时间内信号所经历的几何距离;XB(t0)为t0时刻B船的位置;XA’(tA)为tA时刻A船的位置;dBA为B船发射天线中心到A船接收天线中心的几何距离;ΔdBA为B船发射天线中心到A船接收天线中心的几何距离改正:
dBA=XA(t0)-XB(t0)
(10)
对dBA’按泰勒公式在t0处展开到二阶,即加速度的一次幂有
(11)
则
ΔdBA=dBA′-dBA
(12)
则由几何距离改正引起的时延ΔτBA为
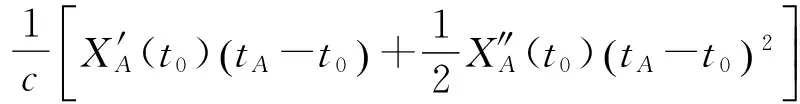
(13)
双向时间同由式(3)的第6项和第7项可知,双向时间同步时延为收发双方时延差的一半,所以由于两舰运动引起的时延误差为

(14)
由式(14)可知,两舰运动引起的时延误差与两船的运动速度,信号在两船之间传输的时间,两船的加速度有关。目前,最快的舰艇速度约为30m/s。海面航行,两船距离一般在几十公里之内,也取最远可视距离300km为例,则信号在两船之间传输的时间为
t=d/c=300×1000/300000000=1×10-3s
由式(11)的第1项和第2项可知,时延误差与两船的相对速度有关。在同一舰艇编队中,所有舰艇的航行方向一致,相对速度为0,所以,假定B船运动,A船静止,两船速度差最大,则
=5×10-11s=0.05ns
所以节点(舰船)的速度对时延误差的影响在0.05ns之内,而对于加速度项的影响更是微乎其微,在皮秒量级,在此可以忽略不计。
4 结语
通过对信号传输路径分析,影响时间传递精度的主要误差有设备的系统误差,该项误差可以通过修正、温度控制和对数据的温度补偿得到降低[10];信号空间传播路径上的误差,主要是空间大气折射率引起的时延,该项误差经理论计算约几个ps,但实际受温度、湿度、大气压强、雨、雪、雷、电等多因素影响,误差远远超出理论推算,需要经过实际测量,大量的数据统计计算,得出估计值,该项误差不属于系统误差,不可修正;信号在传播过程中舰船的运动引起的时延误差,该项误差随海面两运动站点的相对运动方向、速度和加速度改变,可以通过建模,数学计算得到修正,但是海面运动状态不可预知,海上舰船在涌浪、风、自身重力作用下,在空间进行三维运动,为了保证数据使用的安全性,在实际应用中尽量扩大一些。综上分析,由于舰船在海面运动引起的时间同步精度在0.05ns之内,该理论分析、计算为今后建立海面运动舰艇之间的时间同步系统提供理论依据。
[1] 中国人民解放军总装备部军事训练教材编辑工作委员会.时间统一技术[M].北京:国防工业出版社,2004.
[2] 黄波,胡修林.北斗2导航卫星星间测距与时间同步技术[J].宇航学报,2011,32(6):1271-1275.
[3] 武文俊.卫星双向时间频率传递的误差研究[D].西安:中国科学院国家授时中心,2012.
[4] 张升康,王学运,王宏博等.卫星双向时间频率传递校准技术综述[J].宇航计测技术,2013(1):15-22.
[5] 李学森,付庆霞.双/多基地雷达系统同步技术[J].舰船电子对抗.2007,30(4):51-54.
[6] 董绍武,漆溢,刘春侠等.临潼一蒲城数字微波时间传输系统建设及初步结果[J].时间频率学报.2008,31(2):105-110.
[7] 车爱霞,微波时间传递精度和时延分析[J].时间频率学报,2009,32(1):12-17.
[8] Achkar J. A New Microwave Satellite Simulator for the determination of delays in a TWSTFT Station[C]//Microwave Conference, 2008. EuMC 2008. 38th European. IEEE, 2008: 1034-1037.
[9] D.Piester, A.Bauch, M.Fujieda et al. Study on instabilities in long-baseline two-way satellite time and frequency transfer(TWSTFT) including a troposphere delay model[C]// In Proc.39th Ann. PTTI Meeting, 2007 :211-222.
[10] 苗苗,周渭,李智奇,等.用于时间同步的高精度短时间间隔测量方法[J].北京邮电大学学报,2012,35(4):77-80.
Influence of Time Synchronous Precision Caused by Ship Moving
FU Yongjie YU Meng LI Di
The paper is aimed at the matter that the high precision time synchronous is very important, and the two-way microwave time transfer (TWMTT) is selected as the time synchronous method for moving ship. Through analysis of signal transfer link, the principle of TWMTT is described. The influencing factors of time synchronous precision are deduced. Delay errors caused by ship moving are analyzed in detail. The mathematical model of delay error caused by ship moving is set up. Through the second-order expansion Taylor, the delay error caused by movement velocity and acceleration of ships are deduced. Through theoretical analysis and calculation, the delay error caused by ship moving of TWMTT is below 0.05ns, which can provide theory basis for establishing time synchronization system between moving ships on sea.
time synchronization, delay error, ship moving, Taylor formula
2016年6月18日,
2016年7月21日
付永杰,女,博士,高级工程师,研究方向:时间频率计量与测试,兵器科学与技术。于蒙,男,工程师,研究方向:无线电计量与测试技术。李迪,男,硕士,助理工程师,研究方向:力学计量与测试技术。
TB939
10.3969/j.issn.1672-9730.2016.12.017
