飞行目标航迹显示中的数据拟合方法*
2017-01-11陈庆良姬新阳
陈庆良 高 山 姬新阳
(1.中国洛阳电子装备试验中心 洛阳 471003)(2.西安卫星测控中心 西安 710043)
飞行目标航迹显示中的数据拟合方法*
陈庆良1高 山2姬新阳1
(1.中国洛阳电子装备试验中心 洛阳 471003)(2.西安卫星测控中心 西安 710043)
试验任务中,一个飞行目标往往是多台测量设备同时跟踪测量,产生基于不同设备的同时刻同目标的多批真值数据,其拟合问题在航迹显示的数据处理过程中尤为重要。论文以6台测量设备的航迹数据为例,给出了数据拟合模型及计算机求解算法,并进行了仿真,结果表明拟合后的数据更接近目标真实,为今后研究多台套测量设备数据拟合,提高航显精度与时效奠定了基础。
测量; 航迹显示; 数据拟合; 牛顿迭代法; 海塞矩阵
(1. Luoyang Electronic Equipment Test Center of China, Luoyang 471003)
(2. Xi’an Satellite Control Center, Xi’an 710043)
Class Number V557
1 引言
飞行任务中目标飞机按照任务要求沿预设航迹飞行,多台测量设备同时跟踪,这些测量设备将测量结果实时送到指控中心,指控中心的指挥控制系统会把其中一路数据作为飞机航迹显示的数据源,并将飞行轨迹在电子地图上显示出来。如图1、图2,六台设备参与对飞行目标的测量。只有一台设备的数据用于航迹显示,其他设备的数据仅仅用作备份。但这些测量设备受到自身性能和环境条件等客观因素的影响,测量结果均存在测量误差[1~4],在某些特定情况下也会失真或者丢点,究竟哪一台设备更能反映目标的真实位置?是否应该以6台设备的测量结果为参照,拟合出一批数据作为描述目标位置的最终依据?

图1 同一时刻六台设备测量试验示意图

图2 同一时刻六台设备测量试验数据流程图
2 建立模型
2.1 数学描述
由于六台测量设备的数据参数和采样频率不同,特作如下统一: 1) 将不同坐标系下的参数转化为同一坐标系; 2) 统一采样时间,在同一时刻对不同设备的数据进行取样[6~12]。
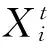
t时刻拟合出的参数向量为
其中,T表示一次试验中采样时间片的最大值,作一点说明,在其他应用模型中向量的分量可能不仅仅只有三个,本模型假设对所有的设备而言,它们描述飞行目标的共性是都含有或都可以转化为某个坐标系下的x1、x2、x3三个分量。
2.2 参数分析
虽然各测量设备的测量结果不尽相同,但是也不会相差太远。一般情况下,各参数总是在一定的空间范围内波动,各设备参数的位置分布情况可用图3表示。

图3 各设备测量数据分布示意图
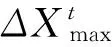

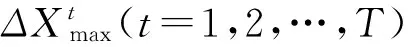


图5 测量数据的内在关系示意图
2.3 建立模型


图6 拟合点到各测量点距离示意图
显然有下列不等式成立


如果在球体内求得的这一点Xt,使得
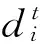
其中
3 计算机求解
3.1 牛顿迭代法[16]
Newton迭代法的计算公式如下

迭代终止条件
‖Xk+1-Xk‖≤ε
ε是一个精度控制量,一般取值为10-1~10-6之间,根据实际需要确定ε的大小来控制求解精度。
3.2 初始值选择
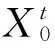
3.3 海塞矩阵求解[17]
首先作如下一些简记
算法步骤:
1) 输入精度ε,对i=0,1,2,完成如下步骤:
2) 对j=0,1,2,完成如下步骤:
3)h=1,f=0;
4) 置f⟹ftemp,求出fi,fj,fij,fx;
5) (fij+fx-fi-fj)/h2⟹f,h/2⟹h;
6) 如果|f-ftemp|<ε转7),否则转4);
7)f⟹aij;
8)j+1⟹j转3);
9)i+1⟹i转2);
10) 返回矩阵[aij]首地址a00。
图7为一个运用上述算法求解的实例结果,从图中可以看出,数据拟合效果更接近真实值。
4 结语
本文以六台跟踪测量设备确定飞行目标航显数据的试验任务为例,采用数据拟合方法确定目标航迹,建立数学模型并给出计算机求解算法,所得结果比较接近飞机的真实位置。克服了单选跟踪测量设备,定位精度不高的弊端,对于进一步研究多台套测量设备数据拟合,提高航显精度问题提供了参考。

图7 拟合求解结果界面
[1] 方棉佳,吕涛.单脉冲和差波束测角的精度研究[J].雷达科学与技术,2013,11(6):645-649.
[2] 仇维礼.数据处理和误差分析[M].北京:知识出版社,1986.
[3] 张方仁,张金通.测量误差的统计分布和检验[M].北京:中国计量出版社,1992.
[4] Alan Jennings.工程和科学的矩阵算法[M].北京:清华大学出版社,1985.
[5] 马慧萍,王永海,张伟.一种实时目标跟踪航迹数据融合算法[J].计算机仿真,2010,11(11):44-46.
[6] 韩崇昭,朱洪艳,段战胜.多源信息融合[M].北京:清华大学出版社,2010.
[7] 盛丹,王国宏,王娜.一种基于模糊数据关联的粒子滤波算法[J].电光与控制,2010,17(4):34-38.
[8] 贺正洪,雷英杰,雷蕾.基于直觉模糊聚类的数据关联算法[J].计算机应用,2011,31(3):647-650.
[9] 贺宏锟,史浩山.基于关联矩阵的网络拓扑辨识方法研究[J].西安交通大学学报,2006,40(4):477-480.
[10] 司锡才,陈玉坤,李志刚.数据关联算法的研究[J].哈尔滨工程大学学报,2007,28(7):813-817.
[11] 刘利军,沈毅,赵振昊.基于多项式拟合SDRE的三维导引律设计[J].宇航学报,2010,31(1):87-92.
[12] P Willett, R Niu. Y Bar-Shalom Integration of bayes detection with target tracking,2001.
[13] 华东师范大学数学系.数学分析[M].第三版.北京:高等教育出版社,2004.
[14] 杨文杰,孙静.多元函数的极值问题[J].辽宁工学院学报,2004,24(1):27-30.
[15] 贺宏锟,史浩山.基于关联矩阵的网络拓扑辨识方法研究[J].西安交通大学学报,2006,40(4):477-480.
[16] 邓先礼.最优化技术[J].重庆大学出版社,1998:136-141.
[17] 丁丽娟.数值计算方法[J].北京理工大学出版社,2000:150-153.
Data-fitting Method in the Flight Path Display
CHEN Qingliang1GAO Shan2JI Xinyang1
In some equipment test, multi-group data are obtained by many sets of measuring equipment that track a same flying target at the same time. It is valuable how to fit these data to form a new one for computer better displaying the flight path. This paper puts forward a data fitting model and a computer calculating method, through an example of six groups of data fitting. The simulation results show that the fitting effect is more close to the real value. As a future reference, this paper provides a way for accurately and efficiently solving more data fitting problem.
measure, flight path display, data fitting, Newton method, Hessian Matrix
2016年6月5日,
2016年7月25日
陈庆良,男,工程师,研究方向:指挥控制和雷达测量。
V557
10.3969/j.issn.1672-9730.2016.12.013
