粒子群算法优化混合核函数SVM及应用*
2017-01-11崔国恒李京书
崔国恒 李京书 张 军
(1.海军工程大学 武汉 430033)(2.空军装备研究院 北京 100000)
粒子群算法优化混合核函数SVM及应用*
崔国恒1李京书1张 军2
(1.海军工程大学 武汉 430033)(2.空军装备研究院 北京 100000)
相比于单一核函数支持向量机,混合核函数的引入使支持向量机多了一个可调参数,而这个可调参数一般是根据人为随机选取或者依据经验选取,并不能保证参数最优。针对此问题,提出了以惩罚系数、核函数参数和可调参数为寻优对象,用动态粒子群对其进行寻优的方法,以获取最优参数组合,从而提高支持向量机的分类性能。通过对UCI数据库中的IRIS数据集进行分类实验,结果表明:相比于单一核函数支持向量机,混合核函数支持向量机泛化能力更好,分类精度更高;动态粒子群算法能够搜索到更优的支持向量机参数。
支持向量机;动态粒子群;核函数参数;寻优;分类精度
(1. Naval University of Engineering, Wuhan 430033)(2. Equipment Research Department of Air Force, Beijing 100000)
Class Number TP393
1 引言
支持向量机(Support Vector Machine,SVM)是统计学习理论的具体体现,统计学习理论是从小样本出发的学习理论,最早是由Vapnik于20世纪60年代提出的,自20个世纪90年代逐渐受到越来越多的关注[1]。一般的机器学习如神经网络,在训练的过程中目标函数通常遵循最小化经验风险,但真实风险不一定最小,这也是经验风险最小化准则的弊端。而SVM放弃了传统的经验风险最小化准则,采用的是结构风险最小化(Structure Risk Minimization,SRM),SVM对于问题的求解实际上是求一个二次规划问题的最优解。在SVM中,采用核函数构建非线性映射很好地解决了线性不可分问题[2]。SVM已经在如基因分析、手写体数字识别、人脸识别等很多领域取得了成功应用[3]。
SVM作为一种较为新颖的机器学习方法,目前存在的主要问题是核函数的选取和参数的优化。对于一些数据集,不同的核函数选取方式对分类结果的影响较为相近;而对另一些数据集来说,选取不同的核函数对分类结果的影响很大。对于不同的数据集,需要选取什么样的核函数并没有统一的解决方法。另外,SVM参数的选取也没有确定的参考标准。因此,核函数的选取以及参数的优化对提高SVM性能就显得尤为重要。粒子群(Particle Swarm Optimization,PSO)算法是基于群体中粒子间的合作和竞争而进行参数优化、搜索的,它是一种较为有效的全局寻优算法[4]。但是,PSO算法容易早熟、陷入局部最优,导致最终搜索到的参数最优解不是全局最优解[5]。考虑以上因素,本文提出混合核函数SVM,并用动态粒子群(DPSO)算法对其参数进行寻优。
2 混合核函数
核函数是指非线性映射函数K(·),它能将低维空间中的线性不可分问题转化到高维空间中,从而变为线性可分问题。核函数的引入极大的提高了SVM对非线性问题的处理能力。SVM主要有全局和局部两种核函数类型,主要分为四种[6]:
1) 多项式(Polynomial,POLY)核:
K(x,xi)=(xxi+1)d
2) RBF(Radial Basis Function)核:
3) 线性核
K(x,xi)=xxi
4) Sigmoid核
K(x,xi)=tanh(k(xxi)+θ)
RBF核函数属于局部核函数,其学习能力强,泛化能力弱,它是一般的SVM最常用的核函数;与RBF核函数不同,线性核函数、POLY核函数、Sigmoid核函数属于全局核函数,其学习能力弱,泛化能力强[7]。当数据之间距离较远的点对SVM分类效果影响较大时,此时应选用全局核函数;当数据之间距离较近的点对SVM分类影响较大时,此时应选用局部核函数。来源于神经网络的Sigmoid全局核函数只有在它的参数达到特定条件的要求时,才符合对称、半正定的核函数条件,它在解决实际问题的过程中常受到限制[8~9]。所以,考虑将局部核RBF核函数和全局核POLY核函数组合起来,形成一种新的核函数以达到同时兼顾学习能力和泛化能力的目的,本文提出一种新的混合核函数为
Kmix=(λ/2)2·KRBF+[1-(λ/2)2]·KPOLY
其中参数λ用来调节RBF核函数和POLY核函数在混合核函数所占的比重,它决定了RBF核函数和POLY核函数所发挥的作用的大小。因为KRBF、KPOLY满足对称、半正定,可以证明,Kmix满足对称、半正定的Mercer条件。当λ=0时,混合核函数变为POLY核函数;当λ=2时,混合核函数变为RBF核函数。这里确定参数λ的取值范围为[0,2]。则混合核SVM需要优化的参数有可调参数l、RBF核参数γ、POLY核参数d以及惩罚系数C。
3 动态粒子群算法(DPSO)
(1)
(2)
其中,d=1,2,,K;i=1,2,,N分别为搜索空间维数和种群规模;r1,r2是介于(0,1)之间的随机数;c1,c2为学习因子常数,ω为惯性权重。
针对PSO算法运行过程中,粒子群多样性下降较快及算法容易陷入局部最优的问题,刘建华等根据粒子之间的相似度对算法进行改进,使粒子群算法能够在运行过程中动态地调整自身的搜索能力,提高收敛速度和搜索精度,以达到更好的性能[11]。定义1、定义2分别是刘建华等给出的粒子间相似度定义和惯性权重ω′的计算公式,定义3是本文给出的惯性权重ω计算公式。
定义1 两个粒子i,j的相似度s(i,j)满足如下条件[12]:
1)s(i,i)=1;2)当d(i,j)→∞时,s(i,j)=0;3)对任意两个粒子i、j,都有s(i,j)∈[0,1]。则粒子之间的相似度s(i,j)满足如下等式:
(3)
其中,d(i,j)为粒子i,j在空间里的欧几里得距离,dmax、dmin分别为粒子间距离的最大、最小值。
定义2 惯性权重ω′的计算公式如下[12]:
(4)
(5)
本文在刘建华等给出的粒子相似度定义的基础上重新定义权重ω,如定义3所示。
定义3 惯性权重ω的计算公式如下:
(6)
其中,s(i,g)为第i个粒子与最优粒子g之间的相似度;ωmax、ωmin分别为惯性权重取得的最大、最小值;tmax为最大进化代数;t为当前进化代数。由式(6)可知,随进化代数t和粒子i与最优粒子间相似度s(i,g)的变化,惯性权重ω∈(ωmin,ωmax),且在算法在运行前期,大部分粒子与最优粒子的距离大于或等于dmax,此时惯性权重大,算法的全局搜索能力强;在运行过程中,随着粒子逐渐向最优粒子靠近,惯性权重随着进化代数非线性减小,模拟粒子的非线性运动过程;在运行后期,粒子越来越接近最优粒子(最优解),此时令惯性权重等于较小的值,进一步保证了算法在较小范围内搜索的精度。刘建华等提出的动态粒子群算法记为DPSO1,本文提出的动态粒子群算法记为DPSO2。
4 DPSO优化混合核函数SVM方法
应用DPSO算法优化SVM的流程图如图1所示。DPSO算法适应度函数为SVM分类准确率的最大值,这样DPSO算法就会将使SVM具有最大分类能力的参数组合作为搜索目标。
5 仿真实验与结果分析
5.1 数据来源
本文采用UCI数据库中的IRIS数据集进行分类实验,IRIS数据集是以鸢尾花的特征作为数据来源,包含150个数据样本,分为Iris-setosa、Iris-versicolor、Iris-virginica等3类,每类有50个样本,每个样本包括4个属性:萼片长度、萼片宽度、花瓣长度、花瓣宽度[13]。
5.2 实验结果与分析
模型中,设置混合核函数SVM参数范围为λ∈[0,2];C∈[2-10,210];γ∈[2-10,210];d∈[1,10]。设置DPSO算法参数范围为c1=1.5,c2=1.5;ω∈[0.2,1];种群大小为25;进化代数为50。实验中,随机选择IRIS数据集中Iris-setosa样本25组、Iris-versicolor样本25组、Iris-virginica样本25组作为训练集,剩下的作为测试集,以检验SVM的分类性能和泛化能力。分别利用刘建华等提出的DPSO1算法和本文提出的DPSO2算法搜索SVM的最优参数,实验重复进行20次,得到混合核函数SVM算法、RBF核函数SVM的分类正确率及算法运行时间分别如图2、图3所示。
同时,由仿真实验可以得出,当可调参数λ的取值范围为(1.5,2)时,混合核函数SVM具有更好的分类准确率。
从图2、图3可以看出,混合核函数DPSO-SVM的分类准确率/运行时间总体上比单一RBF核函数DPSO-SVM的分类准确率/运行时间高/长,计算出20次实验混合核函数DPSO1-SVM、混合核函数DPSO2-SVM的分类准确率的平均值分别为96.0667%和97.4667%;运行时间平均值分别为24.2711s和24.1817s。计算出单一RBF核函数DPSO1-SVM、单一RBF核函数DPSO2-SVM的分类准确率平均值分别为91.8000%和92.7333%;运行时间平均值分别为1.7219s和1.7100s。不同算法的分类准确率均值和运行时间均值如表1所示。

图1 DPSO-SVM算法流程图


图2 20次实验不同算法准确率对比
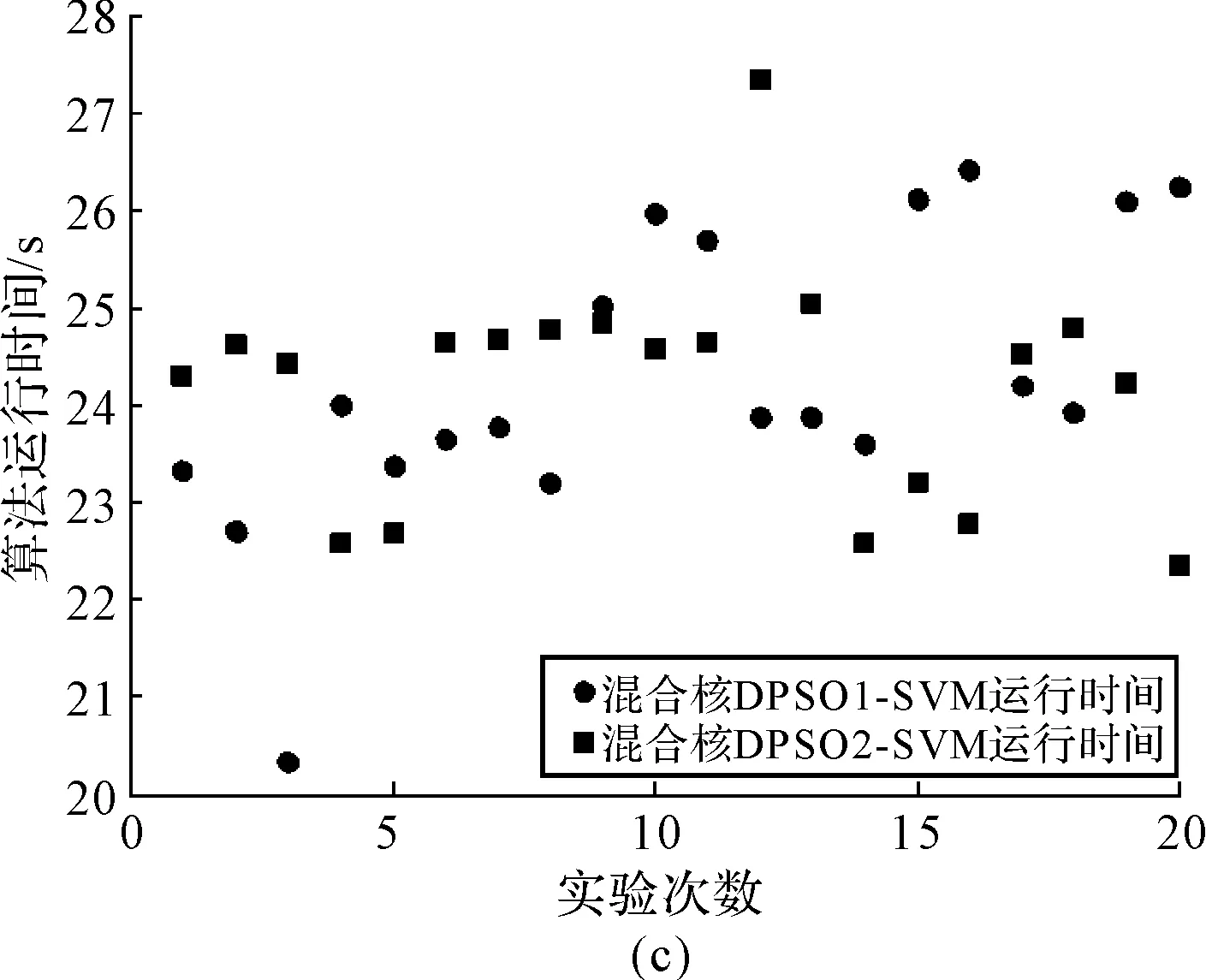
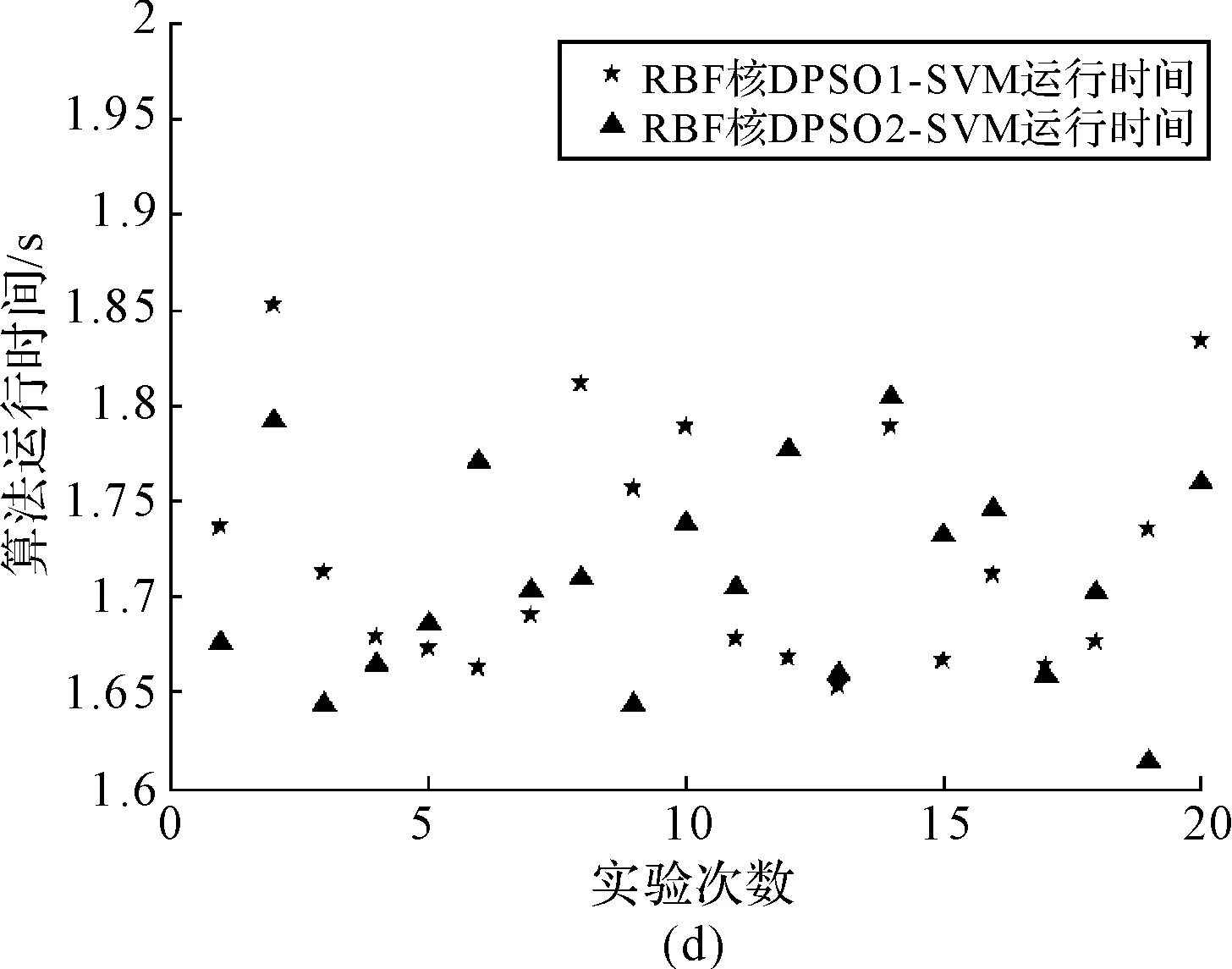
图3 20次实验不同算法运行时间对比
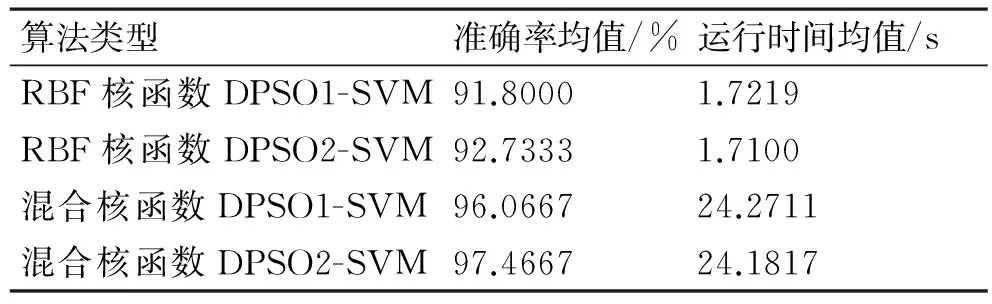
表1 不同算法分类准确率、运行时间均值
从表1中的数据可以看出,在核函数一致的情况下,DPSO2算法优化的SVM平均分类精度/运行速度要比DPSO1算法优化的SVM平均分类精度/运行速度高/快,这说明了本文提出的DPSO2算法要比刘建华等提出的DPSO1算法搜索精度更高,收敛速度更快。在优化算法一致的情况下,混合核函数DPSO-SVM算法的平均分类精度要比单一RBF核函数DPSO-SVM的平均分类精度高,经POLY核和RBF核混合而成的混合核函数使得SVM的分类能力有所提高,推广能力也有所增强。但混合核函数DPSO-SVM算法平均运行时间大约是单一RBF核函数DPSO-SVM算法平均运行时间的14倍。经过以上分析,虽然混核函数DPSO-SVM的分类准确率比单一RBF核函数DPSO-SVM分类准确率高,但是其运行时间要更长。这是因为混合核函数SVM的待优化参数除了惩罚系数C和核函数参数γ外,还增加了权重参数l和POLY核参数d,使得算法的复杂性增加,计算量增大,算法运行起来更加耗时。另外,由表1还可以看出,在相同条件下,不同算法的平均运行时间差异并不是很大,牺牲适当的运行时间来实现算法分类精度的较大提升是完全可以接受的。所以,混合核函数DPSO-SVM算法也是可行、有效的。
6 结语
本文提出了一种新的混合核函数SVM算法,并在DPSO1算法基础上,提出了DPSO2算法,用于搜索SVM的参数。实验结果表明: 1) 相比于DPSO1算法,DPSO2算法的搜索精度更高,收敛速度更快; 2) 相比于RBF核函数SVM,混合核函数SVM的分类性能有所提高。
[1] Theodoros Evgeniou,Massimiliano Pontil,Tomaso Poggio. Statistical Learning Theory: A Primer[J]. International Journal of Computer Vision, 2000, 381.
[2] Jawad S. Alagha,Md Azlin Md Said,Yunes Mogheir. Modeling of nitrate concentration in groundwater using artificial intelligence approach—a case study of Gaza coastal aquifer[J]. Environmental Monitoring and Assessment, 2014, 1861:.
[3] 丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,01:2-10.
[4] 黄少荣.粒子群优化算法综述[J].计算机工程与设计,2009,08: 1977-1980.
[5] 聂立新,张天侠,赵攸.粒子群算法优化双核支持向量机及应用[J].振动、测试与诊断,2014(3):565-569.
[6] Christopher K. I Williams. Learning With Kernels: Support Vector Machines, Regularization, Optimization, and Beyond[J]. Journal of the American Statistical Association, 2003, 98462.
[7] Zheng S, Liu J, Tian J W. An SVM-based small target segmentation and clustering approach[C]//Machine Learning and Cybernetics, 2004. Proceedings of 2004 International Conference on. IEEE, 2004, 6: 3318-3323.
[8] 王行甫,俞璐.混合核函数中权重求解方法[J].计算机系统应用,2015,04:129-133.
[9] Smits G F, Jordaan E M. Improved SVM regression using mixtures of kernels[C]//Neural Networks, 2002. IJCNN'02. Proceedings of the 2002 International Joint Conference on. IEEE,2002,3:2785-2790.
[10] 鲁峰,黄金泉,陈煜,等.基于SPSO-SVR的融合航空发动机传感器故障诊断[J].航空动力学报,2009,08:1856-1865.
[11] 刘建华,樊晓平,瞿志华.一种惯性权重动态调整的新型粒子群算法[J]. 计算机工程与应用, 2007, 07: 68-70.
[12] 刘建华.粒子群算法的基本理论及其改进研究[D].长沙:中南大学,2009.
[13] 刘春卫,罗健旭.基于混合核函数的PSO-SVM分类算法[J]. 华东理工大学学报 (自然科学版), 2014, 1: 017.
Particle Swarm Algorithm to Optimize the Kernel Function SVM and Its Application
CUI Guoheng1LI Jingshu1ZHANG Jun2
Compared to single kernel function of support vector machine (SVM), the introduction of the mixed kernel function of SVM has one more adjustable parameters. And the adjustable parameter is usually selected on the basis of human or experience, which does not guarantee the optimal parameters. In order to find the optimal parameters and improve ability of classification of SVM, the parameters of the mixed kernel of SVM are selected by dynamic particle swarm optimization. The classification experiment results show that compared to a single kernel of SVM, the hybrid kernelof SVM has better generalization ability and higher classification accuracy, dynamic particle swarm algorithm can search better parameters of SVM.
support vector machine, dynamic particle swarm, kernel function parameter, optimizing, classification accuracy
2016年6月7日,
2016年7月19日
崔国恒,男,博士,讲师,研究方向:无线电技术及研究。
TP393
10.3969/j.issn.1672-9730.2016.12.011
