具有不同输入时延的二阶多智能体系统一致性
2017-01-11姚佩阳空军工程大学信息与导航学院西安710077
王 品,姚佩阳(空军工程大学信息与导航学院,西安710077)
具有不同输入时延的二阶多智能体系统一致性
王 品,姚佩阳
(空军工程大学信息与导航学院,西安710077)
研究了具有不同时变输入时延的二阶连续多智能体系统的一致性问题。首先,通过变量转换,将系统的收敛性问题转化为误差系统的稳定问题;然后,通过对系统进行变换,将二阶系统稳定性问题转换为等价系统的稳定性问题。通过构造李雅普诺夫函数,基于线性矩阵不等式(LMI)的方法,给出在无向固定拓扑条件下,系统达到一致的充分条件。最后,仿真实例证明了结果的有效性。
一致性;多智能体系统;不同时变输入时延;LMI
0 引言
近年来,一致性问题引起众多学者的广泛关注。一致性问题是指多智能体在动态网络中通过协调控制使其状态达到一致,譬如,多智能体运动过程中的速度趋同、位置趋同,飞行器的集结、蜂拥等。
在一致性的应用中,不可避免地会碰到时延的问题。多智能体自身接收及处理收到信息会产生输入时延;此外,由于信息的传递需要时间,也会产生通信时延。具有时延的一阶智能体系统已得到深入研究,并取得丰硕成果[1-6]。然而,针对具有时延的二阶多智能体系统的研究则相对较少。文献[7]利用频域分析的方法,研究了具有对称、时不变时延下的二阶多智能体系统一致性问题。在文献[8]中,进一步研究了时变时延情况下的系统收敛判据。文献[9]讨论了无向和有向二阶多智能体系统的通信时延上限。针对具有不同通信时延的二阶系统,文献[10]给出了系统达到一致的充分条件。
在实际的物理系统中,各智能体的输入时延并不相同。因此,本文研究了无向拓扑中,在固定拓扑的情况下,具有不同输入时延的二阶多智能体系统的一致性问题。通过构造Lyapunov-Krasovskii函数,利用Lyapunov稳定性判据,得到存在不同输入时延情况下的二阶多智能体连续系统一致性的充分条件,并用线性矩阵不等式表示,利用Matlab自带的LMI工具箱可以得到不同时变时延的上界。
1 预备知识及问题描述

考虑n个智能体组成的二阶连续系统:
(1)
其中,xi(t)∈R和vi(t)∈R分别表示多智能体的位置和速度,ui为控制输入。
2 一致性协议
针对不同时变输入时延,采用无相对速度信息的一致性协议:
(2)
式中,k>0为控制增益,τi(t)为第i个智能体的时变输入时延。因无向图G为连通图,因此,若达到一致,当t→∞时,vi(t)→0,xi(t)→ε,i=1,2…,n。本文考虑的输入时延τi(t)具有以下条件:
2)0≤τi(t)≤hi,i=1,2,…,n,hi>0
写成矩阵形式表示为:
(3)
式中:x(t)=[x1(t),x2(t),…,xn(t)]T,v(t)=[v1(t),v2(t),…,vn(t)]T,矩阵Ii为n×n阶矩阵,其第i行对应单位阵的第i行,其余值为0;Li的定义与之类似,其第i行对应拉普拉斯矩阵L的第i行,其余值为0。
令x(t)=ε1n+Δ(t),式中,Δ(t)=[Δ1(t),Δ2(t),…,Δn(t)]T,1n=[1,1…,1]T。于是,式(3)等价为
(4)
令y(t)=[ΔT(t),vT(t)]T,式(4)又可改写为
(5)。
3 一致性判据
为得到本文结论,首先引入两个引理:
引理1[11]给定矩阵M,P,Q,D,E,且Q>0,E>0则:
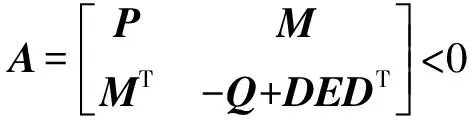
引理2[12-13]对任意可微向量x(t)和任意常数对称矩阵W>0,下列不等式成立:
定理1当时变输入时延满足条件(1)时,对于连通无向图G,应用协议(3),使得下列线性矩阵不等式
(6)
成立,则二阶连续多智能体系统能够达到一致。
证明:考虑Lyapunov-Krasovskii函数(7):
(7)
则求导可得:
(8)
由引理2可得式(9):
(9)
将式(5)代入可得:
(10)
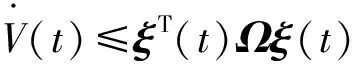
(11)

当输入时延τi(t)满足条件(2)时,选择Lyapunov-Krasovskii函数(12):
(12)
类似于定理1的证明,可得推论1:
推论1对于无向连通图,存在合适的hi使系统(3)达到一致,最大时延hi可通过下列线性矩阵不等式获得:
由于缺少时延导数上界信息,使得式(12)比式(7)少了一个积分项,因此,求得的系统稳定所允许时变输入时延上界具有更大的保守性。
4 计算机仿真实验
下面给出Matlab仿真实验以验证结论的有效性和正确性。一致性协议中k=1,多智能体间通信拓扑结构如
图1所示。 多智能体系统含有5个智能体,固定无向拓扑以及边的权重如图1所示。

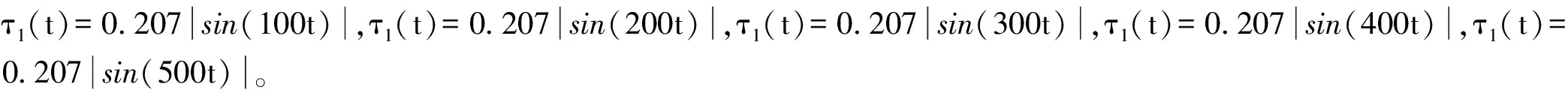
5 结论
本文针对具有不同输入时延的二阶连续多智能体系统进行了研究。通过线性矩阵不等式的方法,得到了在固定无向连通拓扑条件下,具有时延导数信息和无导数信息时,多智能体系统能够达到平均一致性的充分条件,最后仿真验证了结果的有效性。
[1]Olfati-Saber R ,Fax J A,Murry R M.Consensus and cooperation in networked multi-agent systems[C].The Proceedings of the IEEE,2007.
[2]Sun Y G,Wang L.Consensus of multi-agent systems in directed networks with nonuniform time-varying delays[J]. IEEE Transactions on Automatic Control,2009,54(7):1607-1613.
[3]Meng Z Y,Ren W,Cao Y C.Leaderless and leader-following consensus with communication and input delays under a directed network topology[J].IEEE Trans on System, 2010,41(1):75-88.
[4]Tian Y P,Liu C L.Consensus of multi-agent systems with deverse input and communication delays[J].IEEE Trans on Automatic Control,2008,53(9):2122-2128.
[5]梁有明,刘成林.具有通信时延和输入时延的一阶多自主体的一致性[J].信息与控制,2012,41(1):14-21. Liang Youming,Liu Chenglin,Liu Fei.Consensus problem of first-order multi-agent systems with communication delay and input delay[J].Information and Control,2012,41(1):14-21.
[6]曾耀武,冯伟.具有时滞和不确定性多智能体鲁棒一致性研究[J].复杂系统与复杂性科学,2013,10(3):75-80. Zeng Yaowu,Feng Wei.Robust consensus analysis of multi-agent systems with both time-delay and uncertainty[J].Complex Systems and Complexity Science2013,10(3):75-80.
[7]Saber R O,Murray R.Consensus problems in networks of agents with switching topology and time-delays [J].IEEE Trans on Automatic Control,2004,49(9):1520-1533.
[8]Bliman P A,Trecate G F.Average consensus problems in networks of agents with delayed communications[J].Automatica,2008,44(8):1985-1995.
[9]Sun Y G,Wang L,Me G M.Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays[J].Systems and Control Letters,2008,57(2):175-183.
[10] Tang Z J, Huang T Z,Shao J L.Consensus of second-order multi-agent systems with nonuniform time-varing delays[J].Neuro Computing,2012,97:410-414.
[11] Boyd B,Ghaoui L E,Feron E,et al.Linear Matrix Inequalities in System and Control Theory[M].Philadelphia: SIAM,1994.
[12] Sun Y G,Wang L,Xie G M.Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays[J].Systems and Control Letters,2008,57( 1): 175-183.
[13] Sun Y G,Wang L,Xie G M.Stabilization of switched linear systems with multiple time-varying delays[C]∥Proceedings of the 45th IEEE Conference on Decision and Control. San Diego,USA,2006: 4069-4074.
(责任编辑 李进)
Consensus of Second-Order Multi-Agent Systems with Multiple Input Delays
WANG Pin,YAO Peiyang
(Information and Navigation College,Air Force Engineering University.Xi’an 710077, China)
A consensus problem is discussed about the second-order multi-agent system with multiple time-varying input delays.Firstly,by variable transformution,the convergence problem of second-order multi-agent systems is converted into the stability problem of an error system.Then,by system transformution,the stability problem of the second-order system is converted into the stability problem of the equivalent system. Based on linear matrix inequalities (LMI),by constructing Lyapunov-Krasovskii functions,sufficient conditions of consensus in undirected networks are obtained. At last,examples are given to demonstrate the effictiveness of the conclusion.
consensus; multi-agent systems; multiple time-varying input delays; linear matrix inequalities

10.13306/j.1672-3813.2016.04.014
2015-09-28;
2015-11-09
国家自然科学基金(61273048)
王品(1992-),男,山东莱阳人,硕士研究生,主要研究方向为有人/无人协同、多智能体系统一致性。
TP27
A
