基于CAPM的制造业行业β系数的实证研究

孙金花

摘要：在资本资产定价模型（CAPM）中，β系数反映了单个资产系统风险和整个市场的系统风险之间变动的数量关系，是理解资本市场理论中有关收益——风险关系的关键参数。制造业作为国民经济的根本，制造业行业β系数反映整个行业的期望收益率情况，关系到资本对行业的投入。以江苏制造业行业为研究对象，以22家江苏省制造业上市公司为样本，对2010年1月至2014年12月期的数据资料进行分析处理，并对β系数作回归分析，结果表明江苏省制造业行业β系数小于1。

关键词：资产定价模型；β系数；制造业；资本市场

中图分类号：F832.51；F224

文献标识码：A DOI：10.3963/j.issn.1671-6477.2016.06.0027

在资本资产定价模型（CAPM）中，β系数是反映单个资产的价格变动与资本市场平均价格变动之间关系的指标，揭示了市场上资产的平均价格变动对某个或某类资产价格的影响程度。自CAPM建立以来，这一模型被广泛应用于公司投资管理、绩效评价的研究中。β系数在金融理论和投资实践中具有重要作用，测算和预测β系数可以预计单个资产或资产组合的未来收益率，有利于选择正确的投资决策或对决策作出调整；β系数反映的资产的系统风险是投资组合的真正风险，可以用于对过去投资业绩的评价；β系数代表了资产的一个基本风险因素，可以用于对资产的定价。

制造业是创造价值的核心产业，是支撑经济平稳发展的主要力量，是经济结构调整的主要战场，是实施创新驱动战略的主要领域，制造业的发展直接体现了一个国家或地区的生产力水平和竞争力。江苏省作为全国GDP排名第二的经济大省，坚持发展以制造业为主体的实体经济，制造业规模位居全国前列，对支撑全省经济增长、推动社会进步、增进民生福祉发挥了巨大作用。江苏省“十三五”规划提出，要把江苏建设成为具有国际竞争力的先进制造业基地。随着江苏省制造业的投资规模的扩大，分析测算制造业行业的β系数，研究制造业行业的投资收益率，是进行制造业企业业绩考核、确定行业资本成本的基础，具有重大现实意义。

一、制造业β系数研究综述

夏普[1]、林特纳[2]和莫辛在马科维茨的风险资产组合理论和托宾的两基金分离定理的基础上研究建立了资本资产定价模型（CAPM）。CAPM将资产收益与市场组合（即资本市场均衡状态下的均值—方差有效组合）收益之间的协方差同市场组合收益方差之间的比即β界定为该资产所携带的系统风险。在CAPM中，资产价格由系统风险β来定价，资产的定价以市场为基准，即以市场的β系数是1，资产的β值越大，市场风险溢价越高，定价越高，收益率越大。布卢姆[3]对β系数稳定性和时变性进行研究，选取1926年1月至1968年6月间在纽约证券交易所挂牌上市的股票收益率的月度数据进行分析，认为一段时间内估计出来的β值可能是未来β值的有偏估计；随着组合规模的扩大，β系数预测的准确率随之提高。布卢姆认为单个资产的贝塔系数有可能遵循均值回归过程。利维[4]研究了在纽约证券交易所上市的500支股票在1960年至1970年的周收益率数据，选取52周、26周、13周不同的研究时限，结果表明：股票组合的β系数在较短期（52周）内比单个股票的β系数的稳定性有显著提高，并且组合规模越大，估计期间越长，β系数的稳定性越高。亚历山大和车凡尼[5]对1962年至1975年的纽约证券交易所的500支股票的β系数进行研究，利用β估计值的平均绝对离差来检验β系数的稳定性，结果显示并非估计周期越长，β系数越稳定，最佳的估计时长是4-6年。

施东晖[6]选取了1993年4月27日至1996年5月31日的在上海证券交易所上市的50支股票运用CAPM进行研究，样本股票的系统性风险占总风险的平均比例值高达81.37%，他认为上海股票市场上的风险—收益关系并不符合资本资产定价模式，原因有二：一是上海股票市场的非有效性，二是投资组合的非有效性。沈艺峰和洪锡熙[7]利用CHOU检验方法对深圳交易所1996年度所有上市公司股松的交易数据进行实证分析，认为无论是单个股票还是股票组合，β系数都不具备稳定性，当时中国证券市场的系统风险难以预测。靳云汇、李学[8]选取沪深两市51支股票作为样本，研究表明股票β系数随着上市时间增加基本不趋于稳定，股票β系数随着上市时间推移大多趋于增加，大部分股票β值的稳定性增加。马喜德、郑振龙（2006）[9]以深发展为例研究β系数的均值回归，研究表明：单个证券的贝塔系数是一个遵循均值回归过程的随机变量；贝塔系数虽然是可变的，但是也是可预测的。方匡南等[10]从沪深300成分股中选取了30支股票，运用有序聚类虚拟变量法对其β系数的稳定性进行分析，结果显示其中23支股票的β系数是稳定的，表明我国沪深股市的β系数的稳定性概率高达76.7%。

通过上述的研究可以看出，国外的研究基于成熟的资本市场，研究认为β系数具有稳定性，我国由于资本市场建立时间不长，随着资本市场的扩大和发展，学者的研究也趋向于认为β系数具有稳定性，表明β系数是可预测和可检验的，这就为本文的实证研究奠定了理论基础。

二、制造业β系数研究设计

本文利用CAPM研究制造业行业β系数。标准的CAPM方程表达式为：E（Ri）=RF+β[E（RM）-RF]

其中：E（Ri）是资产i的期望收益率，RF指无风险利率，E（RM）为市场组合的期望收益率，它是指所有的风险资产组成的投资组合，β表示系统风险，是i资产与市场组合收益之间的协方差，即β=cov（Ri，RM）σ2RM。

为了便于分析，假设每一种资产收益率与市场收益率之间存在线性关系，建立“单一指数模型（single-index model）”如下：

Ri=αi+βRM+ε

其中：Ri是江苏省制造业行业的收益率，αi是江苏省制造业行业的收益中独立于市场波动的部分；RM是市场的收益率，ε表示误差项。

（一）样本选取

江苏作为制造业大省，截至2014年底，规模以上工业企业中制造业企业共48082家，在沪深两市上市的江苏制造业企业共172家，鉴于数据的可获得性，本文选取2010年以前上市的归属工业指数（000004）成份股的制造业企业，共27家，因本文的收益率采用月度数据，剔除2010年至2014年期间停牌超过一个月的企业，共22家制造业企业。用月收益率对β系数进行估计，研究时间段选取2010年1月至2014年12月，共60期数据。

（二）变量选取

本文原始数据来源于通达信软件和网易财经，获取2010年1月1日至2014年12月31日的22支股票及工业指数的60组月收益率数据并进行下列计算分析。

1.各支股票的收益率。

Rk，t=lnPk，t-lnPk，t-1

其中Rk，t是k股票t时刻的收益率，Pk，t是k股票t时刻的收盘价，Pk，t-1是k股票t-1时刻的收盘价。考虑股票红利对股票价格的影响，本文在研究中对股票的收盘价进行前复权，得到复权后的收盘价。

2.江苏省制造业行业的加权平均收益率。

Ri，，t=∑Rk，tVkt∑22n=1Vnt

其中：其中Ri，t是江苏省制造业行业在t时刻的收益率，Rk，t是k股票t时刻的收益率，Vkt是k股票在t时刻的流通市值；Vkt∑22n=1Vnt是k股票t时刻的权重，即k股票在t时刻的流通市值占样本池股票总流通市值的比重。

3.市场收益率。在研究β系数的文献中多以上证指数测算市场收益率，本文以制造业行业为研究对象，在选取市场收益率时选取上证的行业指数中的工业指数（000004）作为市场指数测算市场收益率：

RM，t=lnPM，t-lnPM，t-1

其中RM，t是市场t时刻的收益率，PM，t是市场t时刻的收盘指数， PM，t-1是市场t-1时刻的收盘指数。

三、制造业β系数的实证分析

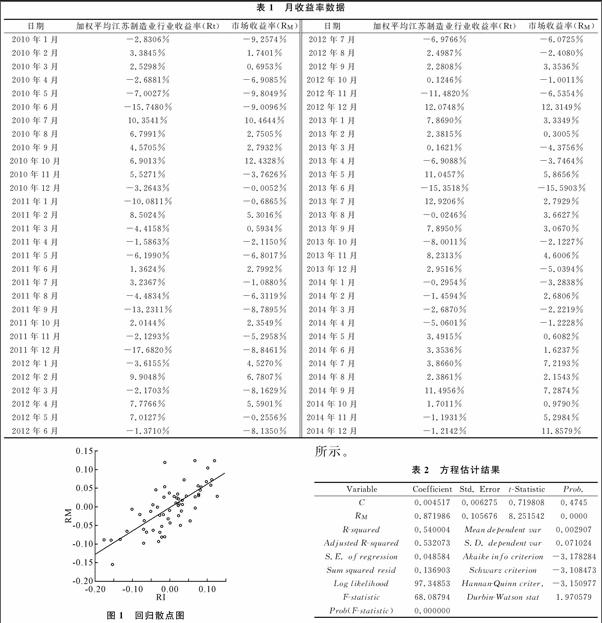
将原始数据按上述研究设计进行计算分析，计算得到的按时间序列的江苏省制造业行业的加权平均收益率（Ri）和市场收益率（RM），具体数据见表1，并用Eviews8.0绘制回归散点图1。

根据图1结果显示，加权平均江苏省制造业行业收益率Ri与市场收益率RM大致满足线性关系。用Eviews进行回归分析，得到结果如表2所示。

四、研究结论

β系数是某项资产的收益率与市场组合之间的相关性，β系数的大小反映了某项资产的收益率对市场收益变化的敏感程度，上述研究的江苏省制造业行业的β系数小于1，说明江苏省制造业行业的收益率变动与中国整个工业市场的收益率变动之间存在相关关系，且江苏省制造业行业收益率的变动幅度小于中国整个工业市场的收益率，即相比于其他地区及其他工业行业，江苏省制造业的收益风险低于整个工业市场平均风险水平。究其原因，主要有以下几个方面：

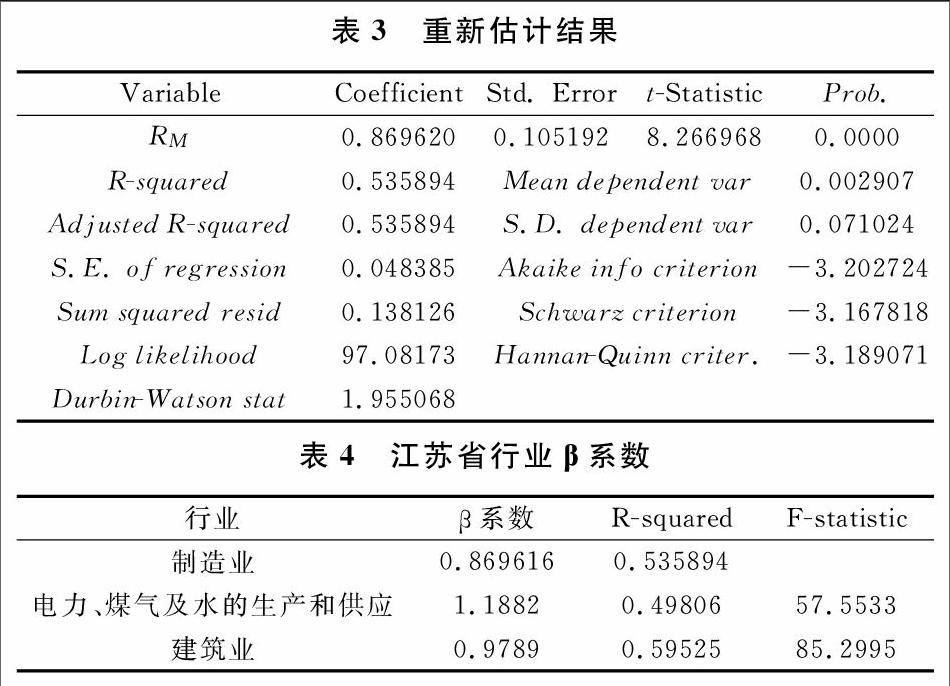
第一，这是由制造业行业本身的特点所决定的。制造业作为实体经济的代表，行业的系统风险是低于其他行业的。江苏省制造业行业β值小于1，这与刘仁和等 [11]对1997年前上市的所有工业类股票共113只进行研究，按月收益率数据回归出的结果一致。江苏省的工业企业的上市公司中，没有采矿业，根据2010年1月至2014年12月的数据信息，分别回归出江苏省电力、煤气及水的生产和供应业行业和江苏省建筑业行业的β系数，见表4。

由上表4可以看出，江苏省制造业行业β系数低于同省的电力、煤气及水的生产和供应行业及建筑行业。这与刘永涛[12]的对上海证券市场的行业β系数研究中的结果不尽相同，是由于江苏省的电力、煤气及水的生产和供应和建筑业的上市公司较少，容易受个股的影响。

第二，分红政策对行业β系数的影响。由于β系数是根据行业收益率的变动情况和市场平均收益率的变动情况之间的关系确定的，所以，在研究计算β系数的时段内，当样本股票发放红利与作为市场收益率的证券指数中的股票发放红利不一致时，β系数会受到影响。当作为市场收益率的证券指数的样本股票中发放红利的股票中所占比例较大时，则发放红利的股票的β系数的计算结果受影响比较小；反之，对于长期不发放红利的股票，所受影响会很大。本文选取的样本股票在研究期间内发放红利较少，如太极实业（600667）五年内只除权除息了四次。

第三，不同时间频率的收益率对行业β系数的影响。本文采用的是月度数据，得出江苏省制造业行业β系数为0.869616。Hawawini分别用不同时限的收益率，包括月收益率、三周收益率、双周收益率、周收益率和日收益率，估计21家公司股票在1970 年1月至1973年12月间的β系数，结果发现存在很大的差异，如柯达（Kodak）股票的β系数用日收益率数据估计时是1.25，而用月收益率估计时则降为0.93。

第四，证券市场的波动对行业β系数的影响。本文的样本数据来自于各上市公司的交易数据，所以分析得出的江苏省制造业行业β系数的相关数据是完全来自于资本市场，应用CAPM 估测β系数同样隐含了一个假设前提：资本市场有效。中国资本市场整体发展水平不够完善，市场机制不够健全，运行效率不高，由此计算分析出的行业收益率不能完全反映整个行业的投资回报率。

综上，本文通过对2010年1月至2014年12月的江苏省制造业行业的β系数进行回归分析，认为此期间江苏省制造业行业的长期β系数为0.869616，小于1，低于市场一般风险，其主要原因在于制造业行业本身特点的影响，分红政策对行业β系数的影响，不同时间频率的收益率对行业β系数的影响，证券市场的波动对行业β系数影响。在供给侧改革的背景下，发展先进制造业，促进产业向中高端迈进，必须扩大有效投入，衡量收益率的一个重要因素就是β系数。

[参考文献]

[1]Sharpe W. F.，Capital Asset Prices： A Theory of Market Equilibrium under Condition of Risk [J].Journal of Finance， 1964（19）：425-442.

[2]Lintner， J.，The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets[J].The Review of Economics and Statistics， 1965.47，13-37.

[3]Blume， E. M. Betas and their Regression Tendencies： Some Further Evidence [J]. Journal of Finance， 1975， 30：785-795.

[4]Levy， R. On the Short-time Stationary of Beta coeiffcients[J]. Financial Analysis Joumal， 1971，27（5）： 55-62.

[5]Alexander，GJ. And N.L.Chervany， On the Estimation and Stabiliy of Beta[J]. Joumal of Financial and Quantitative Analysis， 1980，15（l）：123-137.

[6]施东晖.上海股票市场风险性实证研究[J].经济研究，1996（10）：44-48.

[7]沈艺峰，洪锡熙.我国股票市场贝塔系数的稳定性检验[J].厦门大学学报：哲学社会科学版，1999（4）：62-68，125.

[8]靳云汇，李 学.中国股市β系数的实证研究[J].数量经济技术经济研究，2000（1）：18-23.

[9]马喜德，郑振龙.贝塔系数的均值回归过程[J].工业技术经济，2006（1）：100-101.

[10]方匡南，朱建平，谢邦昌.有序聚类虚拟变量法及其应用[J].数理统计与管理，2012（2）：333-340.

[11]刘仁和，汪永兰，李 刚.上海股市证券贝塔（β）的区间效应[J].当代财经，2003（5）：46-49，56.

[12]刘永涛.上海证券市场β系数相关特性的实证研究[J].管理科学，2004（1）：29-35.

（责任编辑 王婷婷）

Abstract：In the capital asset pricing model （CAPM）， beta coefficient reflects the changes of the quantitative relationship between the systematic risk of individual stock market risk and the market as a whole. And the analysis and research on beta coefficient test in the continuing for many years. The manufacturing industry is the foundation of the national economy. Beta coefficient of the manufacturing industry indicates the expected rate of return of the industry. And it is also related to the capital investment in the industry. In this paper the manufacturing industry of Jiangsu Province is studied as a case. The data from Jan. 2010 to Dec. 2014 of 22 listed companies in Jiangsu Province manufacturing industry are selected as the sample. Then carry on regression analysis of beta coefficient. The results show that the beta coefficient of manufacturing industry in Jiangsu Province is less than 1.

Key words：CAPM； beta coefficient； manufacturing industry； capital market