以斯涅耳定律为例探讨光学中的以点及面教学
2017-01-10王欢欢
武 山,王欢欢
(阜阳师范学院 物理与电子工程学院,安徽 阜阳 236037)
以斯涅耳定律为例探讨光学中的以点及面教学
武 山,王欢欢
(阜阳师范学院 物理与电子工程学院,安徽 阜阳 236037)
本文以斯涅耳定律为例讨论了光学中的以点及面教学方法.通过运用光学中的多个知识点证明斯涅耳定律,展现出了以点及面光学教学的优点.并且通过引入当前的科研前沿,拓展斯涅耳定律的教学内容,从而进一步提高学生的学习兴趣.
光学;斯涅耳定律;以点及面教学
随着知识经济和信息时代的发展,社会对人才的要求也在不断提高.特别是随着光电产业的发展,大学越来越注重光电专业人才的教育.然而,光学课程内容比较繁杂,牵涉的知识面广,致使学生学习困难,教学效果不好.为了更好地理解光学内容,需要在教学过程中综合归纳.特别需要在复习的时候能够以点及面,从一个小的知识点拓展到很大的知识面,既提高了学生的兴趣,又能拓宽学生的知识面,有利于学生对光学知识的整体把握.本文通过对斯涅耳定律的证明为例,拓展光学中的其他知识面,从而做到以点及面的教学.
1 斯涅耳定律
斯涅耳定律(Snell's law)[1],又称折射定律,是荷兰数学家斯涅耳(Snell)在实验中发现的,是在光的折射现象中,确定折射光线方向的定律.其具体内容为(如图1):折射光线、入射光线和法线在同一平面内;折射线与入射线分别在法线的两侧;折射角和入射角满足:

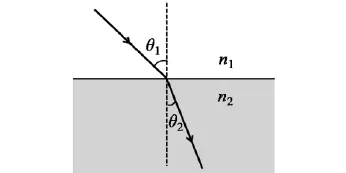
图1 光线折射示意图.其中n1和n2为折射率,θ1和θ2是入射角和折射角.
下面通过证明斯涅耳定律为切入点,介绍光学中的多个知识点.
2 费马原理证明斯涅耳定律
费马原理(Fermat's Principle)是指光在两点间传播,实际走的路线花费的时间是极值(最大、最小和恒定值).其数学表达式为

如图2所示,在折射率为n1的介质中,从A点发出的光线经过C点到达折射率为n2的介质中的B点.AB之间的水平距离设为L,假设C点到达A点的水平距离为x,则到达B点的水平距离为L-x,A点和B点到界面的距离为h1和h2.则光线从A到B的光程L为:
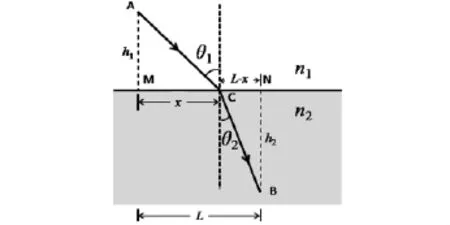
图2 费马原理证明斯涅耳定律示意图
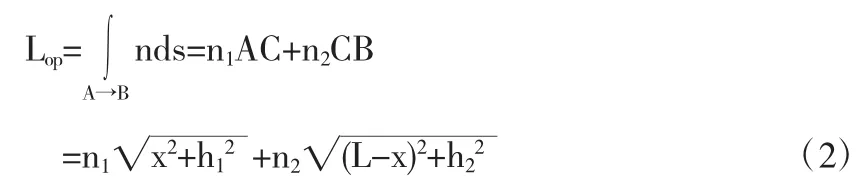
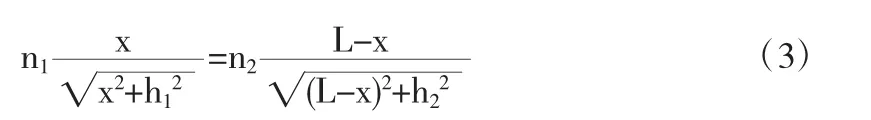
这里,通过证明折射定律学习了几何光学中的最基本的原理——费马原理.
3 惠更斯原理证明斯涅耳定律
惠更斯原理(Huygens'Principle)[1]是指波动传播到的各点都可以看作是发射子波的波源,而在其后的任意时刻,这些子波的包络面就是新的波前.
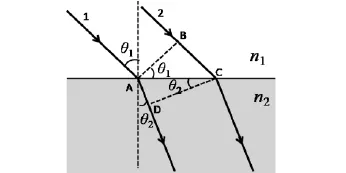
图3 惠更斯原理证明斯涅耳定律的光路示意图
如图3所示,作一入射光的波前AB.根据惠更斯原理,波前AB上的任意两点A和B可以作为子波源.子波源A和B发出的光在相同的时间t内到达D和C点,所组成的新包络面CD即为新的波前.根据几何关系可知

其中υ1=c/n1和υ2=c/n2为光在介质1和2中的速度,c为光速.在(4)式消掉时间t和AC,即可证斯涅耳定律.
在这个实例中,波前、波速的概念和惠更斯原理得到了学习和理解.
4 干涉原理证明惠更斯原理
如图3所示,光线1和2斜入射到界面上,作一波前AB.在波前上,A点和B点是同相的,也就是相位差等于0.根据上面讨论知道,在相同的时间里,A发出的光到达D点,B的到达C点.如果要形成折射波,在C和D点的光波必须相长干涉,否则,会因为相消干涉而消失[2].这就要求光波在C点和D点是同相的,也就是说它们的相位差等于0.即光程差等于0.

其中k1=n1k0和k2=n2k0是光在介质n1和n2中的波矢,k0=2π/λ0是真空中的波矢,λ0是真空中的波长.利用(4)式的几何关系,斯涅耳定律可证.
在这个证明中所用的光学知识有相位差和光程差的定义以及干涉的原理等.
5 动量守恒定律证明惠更斯原理
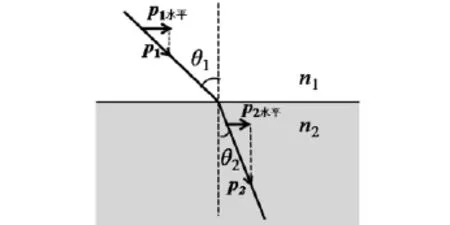
图4 动量守恒定律证明惠更斯原理示意图

其中,
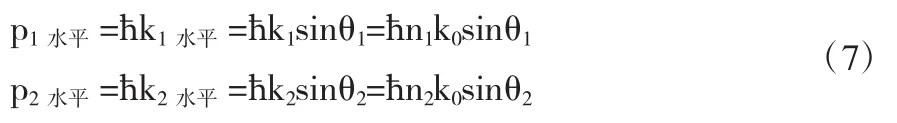
(7)代入(6)式,斯涅耳定律可证.
这这个证明中,学习了德布罗意波、光量子和光动量的概念.
6 变分法证明斯涅耳定律
如图5所示,假设ACB是真实的光线路径,而ADC是无限靠近真实路径的一个虚拟路径.按照变分原理,两条光线在A、B两点相位相同,也就是光线经过两条路径的光程差为0.
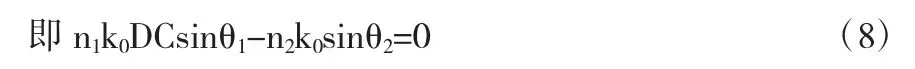
斯涅耳定律可证.
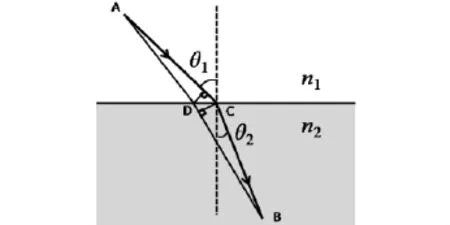
图5 变分法证明斯涅耳定律示意图
7 斯涅耳定律的拓展
斯涅耳定律反映的是在两个介质均匀界面上的折射情况.然而,随着微纳加工技术的发展,人们已经能够调控界面处的相位变化.如果在界面处沿着x轴有一常数相位梯度,那么折射定律就要改写.如图5所示,假设光线在D处,坐标为x,相位变化为Φ,在相邻的C处,坐标为x+dx,相位变化为Φ+dΦ.则(8)式改写为
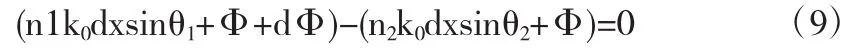
化简得
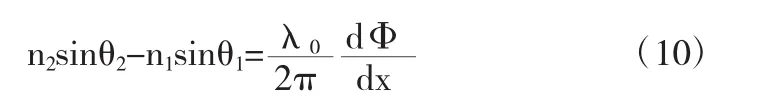
这是广义斯涅耳定律[3].通过设计界面处的相位变化,可以得到任意方向的折射光线.
8 总结
通过斯涅耳定律这一知识点,在证明过程中学习了光学的多个知识点,实现了以点及面的教学.并且通过对斯涅耳定律的拓展,让学生接触到当前的科研前沿,提高学生的学习兴趣,培养学生的科学素养.
〔1〕A.Ghatak.光学[M].北京:清华大学出版社,2010.
〔2〕S.O.Kasap.光电子学与光子学[M].北京:电子工业出版社,2013.
〔3〕N.Yu,P.Genevet,M.A.Kats,F.Aietam,J.Tetienne,F.Capasso,Z [J].Gaburro,Science,2011, 334-333.
G642.0
A
1673-260X(2016)12-0221-02
2016-11-21
