含特定比例均匀随机删失生存数据的SAS模拟实现*

肖媛媛许传志赵耐青

含特定比例均匀随机删失生存数据的SAS模拟实现*

肖媛媛1许传志1赵耐青2△

删失（censoring）是生存分析时经常会遇到的一个实际问题，为生存数据的处理分析带来了一定困难。针对这一问题，在实际研究中往往需要通过随机模拟来产生含一定删失比例的特定生存分布数据，供探索性研究或对比性研究使用。文献检索后发现，目前国内外针对删失生存数据的模拟研究数量较少［1－3］。

按照其发生是否与研究对象的其他特征有关，删失分为随机删失（random censoring）和非随机删失（non-random censoring）两类，即非信息删失（non-informative censoring）和信息删失（informative censoring）［4］。由于非随机删失的影响因素众多，故其特征难以全面捕捉，因此目前在模拟产生含删失的生存分析数据时，大都假定为完全随机删失。

本文针对现有模拟思路和方法中存在的某些问题或疑议，提出一种模拟产生含特定比例均匀随机删失生存数据的思路，以及实现这一思路的SAS宏程序，为科学工作者开展生存分析提供便利。

现有方法回顾

模拟产生含随机删失的生存数据时，步骤一般为：先产生符合特定分布的完整数据，再在此基础上产生删失数据。

生成完整数据时，一般采用的是Bender等2005年提出的模拟方法［5］。该方法的基本思想是，从某一时刻风险函数的一般表达式入手：

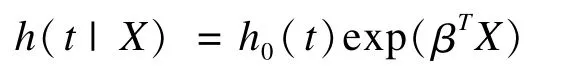
得到当前时刻仍存活的概率为：

假设Y是函数F的自变量，如果生存曲线足够平滑，可以得知服从在［0，1］区间上的均匀分布，同样可得知，1－F（Y）也服从在［0，1］上的均匀分布，即U＝exp［－H0（t）exp（β′X）］服从［0，1］上的均匀分布U［0，1］。

假设生存时间为T，对前式取反函数，得到：

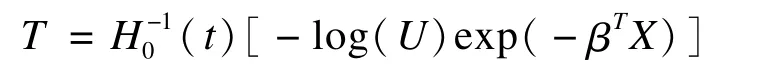
基于上述思想，根据目标生存分布所对应的累积风险函数表达式H0和随机模拟产生的均匀分布U，即可产生目标生存时间。Weibull分布的累积风险函数表达式为：

因此可得到其生存时间T的计算公式为：

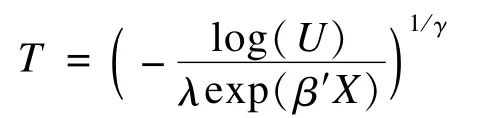
在进一步产生含随机删失的生存数据时，一般的思路为：假设生存时间T和删失时间C服从相互独立的两个分布S（T）和B（C）。在模拟研究中，S（T）的参数已经设定，可以顺利产生生存时间Ti。再根据定义的删失分布类型（即删失发生时间的概率分布），如指数分布或均匀分布，结合设定的删失比例，采用迭代或近似公式计算的方法得到删失时间分布的参数，在此基础上随机产生删失时间Ci。最后通过比较生存时间Ti和删失时间Ci的大小，形成结构为（Ai，Ii）的数据形式。其中，A＝min（T，C），I为指示变量，T＜C时等于1，指代事件发生，T＞C时等于0，指代截尾发生。

不难看出，通过上述模拟方法，确实可以顺利得到随机删失的生存数据，即删失的发生与否与生存时间长短无关。但其在逻辑架构上却存在不恰当之处。其一，我们通过S（T）已经得到了“真实”的生存时间T，而按照定义，删失的发生时间一定是小于真实生存时间的，即C一定小于T。而按照上述方法，将T和C完全当作两个相互独立的分布来模拟，则可能出现C＞T的情况。虽然在上述方法中，正好将这种情况定义为事件发生，但显然已经混淆了真实情况下事件发生的概念。其二，删失分布一定是在真实生存时间T确定的基础上，删失时间C的概率分布，如某观察对象真实生存时间为Ti，又已知其发生了删失，假设其删失分布为均匀分布，则表示Ci在［0，Ti］范围内取任意值的概率相等。因此，上述方法直接在同一时间维度上同时定义真实生存分布和删失分布，同样有悖常理。除此之外，在估计删失分布的参数时，有学者提及的“迭代法”缺乏明确、详细的出处和表述，按照Halabi等提出的公式计算得到的删失分布参数，经实际验证却不能得到预先设定的删失比例［6］。

模拟思路

由于现有模拟方法中存在着如上所述的问题或疑议，我们按照如下思路模拟产生含特定比例均匀随机删失的生存数据：

步骤一：按照如前所述的步骤生成样本含量为N的特定分布的完整生存数据；

步骤二：根据预先设定的删失比例P，在其中随机抽取N×P个观测，作为“删失观测”；

步骤三：每个删失观测的真实生存时间为Ti，由于为均匀删失，因此在［0，Ti］的均匀分布上随机产生其删失时间Ci；

步骤四：将删失观测的删失时间Ci与其他未删失观测的真实生存时间Tj整合为同一变量，定义为观察时间，另外增加指示变量I，I＝1表示发生结局，I＝0表示删失。

SAS模拟宏程序

模拟宏程序以理论生存时间满足Weibull分布为例，读者可自行拓展至指数分布和Gompertz分布，也可重新定义研究变量的数量、类型及参数，程序中只分析了单一的二项分布自变量factor1～B（1，0．5）。

具体程序如下：

讨 论

在当前研究中，我们针对现有删失生存数据模拟方法中存在的问题和疑议，提出了一种含特定比例均匀随机删失生存数据的模拟方法，并给出了实现这一方法的SAS宏程序。经反复验证，这一宏程序能正确产生设定特征的删失生存数据。

模拟产生具有不同删失特征的生存数据，对于探索生存分析方法并验证其价值来说，有着十分重要的意义。在当前研究中，我们仅设定了非常理想化的假设前提：即删失的发生完全随机，且删失分布满足最简单的均匀分布。需要指出的是，在现实情况下，生存数据中删失的发生及其分布特征可能千变万化。虽然无法对每一种可能都进行模拟，但以下两个方向却值得进一步研究：

方向一：同样在完全随机删失的假设前提下，研究不同删失分布类型生存数据的模拟实现，如指数分布、对数分布等。

方向二：在方向一研究的基础上，进一步打破“完全随机删失”这一强假定，探索当删失的发生和理论生存时间之间存在关联，且满足不同的关联模式时，含不同删失比例、不同删失分布生存数据的模拟实现。

［1］高峻，董伟，高尔生，等．多结局生存分析模型与Cox模型的随机模拟比较．中国卫生统计，2007，20（3）：248-251．

［2］钱俊，张超，陈平雁．模拟研究中随机数据的产生及SAS实现．中国卫生统计，2008，21（6）：704-706．

［3］钱俊，刘国庆，周业明．不同删失比例下生存数据模拟生成的方法．数理医药学杂志，2013，26（6）：644-646．

［4］Leung KM，Elashoff RM，Afifi AA．Censoring issues in survival analysis．Annual Review of Public Health，1997，18：83-104．

［5］Bender R，Augustin T，Blettner M．Generating survival times to simulate Cox proportional hazardsmodels．Statistics in Medicine，2005，24（11）：1713-1723．

［6］Halabi S，Singh B．Sample size determ ination for comparing several survival curves w ith unequal allocations．Statistics in Medicine，2004，23（11）：1793-1815．

（责任编辑：刘 壮）

国家自然科学基金（81460519）；云南省自然科学基金（2013FZ064）

1．昆明医科大学公共卫生学院流行病与卫生统计学系（650500）

2．复旦大学公共卫生学院生物统计学教研室

△通信作者：赵耐青，E-mail：nqzhao1954＠163．com